Los fundamentos del aprendizaje profundo en el ejemplo de autoencoder de depuración, número de parte 1

Si lee la capacitación sobre codificadores automáticos en el sitio web keras.io, entonces uno de los primeros mensajes es algo así: en la práctica, los codificadores automáticos casi nunca se usan, pero a menudo se habla de ellos en capacitaciones y la gente viene, así que decidimos escribir nuestro propio tutorial sobre ellos:

Su principal reclamo a la fama proviene de aparecer en muchas clases introductorias de aprendizaje automático disponibles en línea. Como resultado, muchos recién llegados al campo adoran los autoencoders y no pueden tener suficiente de ellos. ¡Esta es la razón por la que existe este tutorial!

Sin embargo, una de las tareas prácticas para las que se pueden aplicar a uno mismo es la búsqueda de anomalías, y personalmente la necesitaba en el marco del proyecto nocturno.

En Internet, hay muchos tutoriales sobre codificadores automáticos, ¿para qué escribir uno más? Bueno, para ser honesto, hubo varias razones para esto:

• Había una sensación de que, de hecho, los tutoriales eran aproximadamente 3 o 4, todo lo demás se reescribió en sus propias palabras;
• Casi todo: en el MNIST'e sufriente con imágenes de 28x28;
• En mi humilde opinión, no desarrollan una intuición sobre cómo debería funcionar todo esto, sino que simplemente ofrecen repetir;
• Y el factor más importante, personalmente, cuando reemplacé MNIST con mi propio conjunto de datos, todo dejó de funcionar estúpidamente .

A continuación se describe mi camino en el que se rellenan los conos. Si toma cualquiera de los modelos planos (no convolucionales) propuestos de la masa de tutoriales y lo pega estúpidamente, entonces, nada, sorprendentemente, no funciona. El propósito del artículo es entender por qué y, me parece, obtener algún tipo de comprensión intuitiva de cómo funciona todo esto.

No soy un especialista en aprendizaje automático y uso los enfoques a los que estoy acostumbrado en el trabajo diario. Para los científicos de datos con experiencia, probablemente todo este artículo será descabellado, pero para los principiantes, me parece que puede surgir algo nuevo.

Empecemos Tengo un conjunto de datos de 4000 imágenes en blanco y negro de 64x64 píxeles, se parece a esto:

Solo algunas líneas sobre un fondo negro, y en la imagen de 64x64 se rellena aproximadamente el 2% de los puntos. Si miras muchas fotos, entonces, por supuesto, resulta que la mayoría de las líneas son bastante similares.

No entraré en detalles sobre cómo se cargó y procesó el conjunto de datos, porque el propósito del artículo, de nuevo, no es este. Solo muestra un fragmento de código aterrador.

# only for google colab %tensorflow_version 2.x import tensorflow as tf import numpy as np import matplotlib.pyplot as plt import os import zipfile import datetime import tensorflow_addons as tfa BATCH_SIZE = 128 AUTOTUNE=tf.data.experimental.AUTOTUNE def load_image(fpath): img_raw = tf.io.read_file(fpath) img = tf.io.decode_png(img_raw, channels=1, dtype=tf.uint8) return tf.image.convert_image_dtype(img, dtype=tf.float32) ## for splitting test/train def is_test(x, y): return x % 4 == 0 def is_train(x, y): return not is_test(x,y) ## for image augmentation def random_flip_flop(img): return tf.image.random_flip_left_right(img) def transform_aug(shift_val): def random_transform(img): return tfa.image.translate(img,tf.random.uniform([2], -1*shift_val, shift_val)) return random_transform def prepare_for_training(ds, cache=True, shuffle_buffer_size=1000, transform=0, flip=False): if cache: if isinstance(cache, str): ds = ds.cache(cache) else: ds = ds.cache() ds = ds.shuffle(buffer_size=shuffle_buffer_size) if transform != 0: ds = ds.map(transform_aug(transform)) if flip: ds = ds.map(random_flip_flop) ds = ds.repeat() ds = ds.batch(BATCH_SIZE) ds = ds.prefetch(buffer_size=AUTOTUNE) return ds def prepare_input_output(x): return (x, x) list_ds = tf.data.Dataset.list_files("/content/planes64/*") imgs_df = list_ds.map(load_image) train = imgs_df.enumerate().filter(is_train).map(lambda x,y: y) train_ds = prepare_for_training(train, transform=10, flip=True) train_ds = train_ds.map(prepare_input_output) val = imgs_df.enumerate().filter(is_test).map(lambda x, y: y) val_ds = val.map(prepare_input_output).batch(BATCH_SIZE, drop_remainder=True) 

Aquí, por ejemplo, está el primer modelo propuesto con keras.io, en el que trabajaron y se entrenaron en mnist:

 # this is the size of our encoded representations encoding_dim = 32 # 32 floats -> compression of factor 24.5, assuming the input is 784 floats # this is our input placeholder input_img = Input(shape=(784,)) # "encoded" is the encoded representation of the input encoded = Dense(encoding_dim, activation='relu')(input_img) # "decoded" is the lossy reconstruction of the input decoded = Dense(784, activation='sigmoid')(encoded) 

En mi caso, el modelo se define así:

 model = tf.keras.Sequential() model.add(tf.keras.Input(shape=(64,64,1))) model.add(tf.keras.layers.Flatten()) model.add(tf.keras.layers.Dense(64*64/10, activation='relu')) model.add(tf.keras.layers.Dense(64*64, activation="sigmoid")) model.add(tf.keras.layers.Reshape(target_shape=(64,64,1))) 

Hay ligeras diferencias entre el hecho de aplanar y remodelar directamente en el modelo, y el de "comprimir" no 25 veces, sino solo 10. Esto no debería afectar nada.

Como una función de pérdida: error cuadrático medio, el optimizador no es fundamental, por cierto, Adam. En adelante, entrenamos 20 eras, 100 pasos por era.

Si nos fijamos en las métricas, todo está en llamas. Precisión == 0.993. Si nos fijamos en los horarios de entrenamiento, todo es un poco más triste, alcanzamos una meseta en la región de la tercera era.

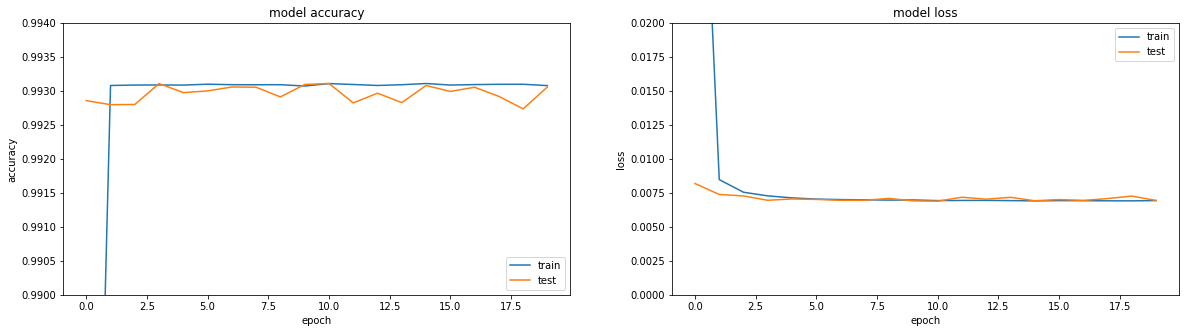
Bueno, si miras directamente el resultado del codificador, obtienes una imagen generalmente triste (el original está en la parte superior y el resultado de la codificación-decodificación está debajo):

En general, cuando intenta averiguar por qué algo no funciona, es un enfoque lo suficientemente bueno como para dividir toda la funcionalidad en bloques grandes y verificar cada uno de ellos de forma aislada. Entonces hagámoslo.

En el original del tutorial: se suministran datos planos a la entrada del modelo y se toman en la salida. ¿Por qué no ver mis acciones sobre aplanar y remodelar? Aquí hay un modelo sin operación:

 model = tf.keras.Sequential() model.add(tf.keras.Input(shape=(64,64,1))) model.add(tf.keras.layers.Flatten()) model.add(tf.keras.layers.Reshape(target_shape=(64,64,1))) 

Resultado:

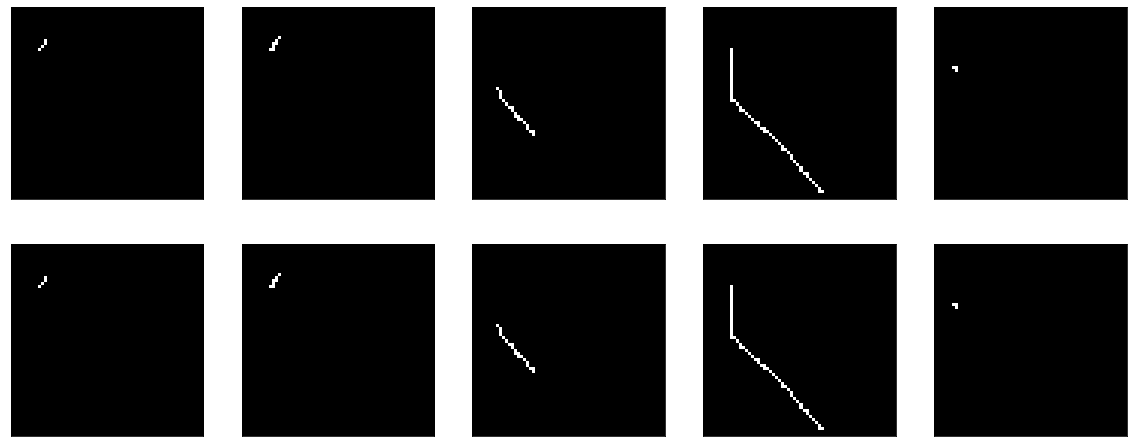
No hay nada que enseñar aquí. Bueno, al mismo tiempo, demostró que mi función de visualización también funciona.

A continuación, intente hacer que el modelo no sea no operativo, sino lo más tonto posible: simplemente corte la capa de compresión, deje una capa del tamaño de la entrada. Como dicen en todos los tutoriales, dicen, es muy importante que su modelo aprenda características, y no solo una función de identidad. Bueno, eso es exactamente lo que intentaremos obtener, simplemente pasemos la imagen resultante a la salida.

 model = tf.keras.Sequential() model.add(tf.keras.Input(shape=(64,64,1))) model.add(tf.keras.layers.Flatten()) model.add(tf.keras.layers.Dense(64*64, activation="sigmoid")) model.add(tf.keras.layers.Reshape(target_shape=(64,64,1))) 

Ella está aprendiendo algo, precisión == 0.995 y nuevamente tropieza en una meseta.

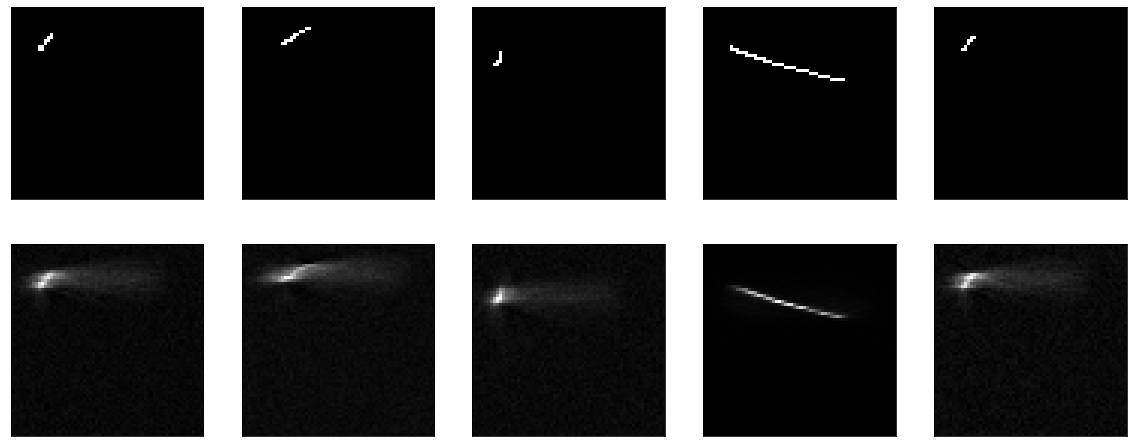
Pero, en general, está claro que no funciona muy bien. De todos modos, qué aprender allí, pasar la entrada a la salida y eso es todo.

Si lee la documentación de Keras sobre capas densas, describe lo que hacen: output = activation(dot(input, kernel) + bias)
Para que la salida coincida con la entrada, dos cosas simples son suficientes: sesgo = 0 y núcleo: la matriz de identidad (es importante no dejar la matriz llena de unidades aquí; estas son cosas muy diferentes). Afortunadamente, esto y aquello se pueden hacer fácilmente desde la documentación para el mismo Dense .

 model = tf.keras.Sequential() model.add(tf.keras.Input(shape=(64,64,1))) model.add(tf.keras.layers.Flatten()) model.add(tf.keras.layers.Dense(64*64, activation = "sigmoid", use_bias=False, kernel_initializer = tf.keras.initializers.Identity())) model.add(tf.keras.layers.Reshape(target_shape=(64,64,1))) 

Porque establecemos el peso de inmediato, entonces no puedes aprender nada, de inmediato es bueno:

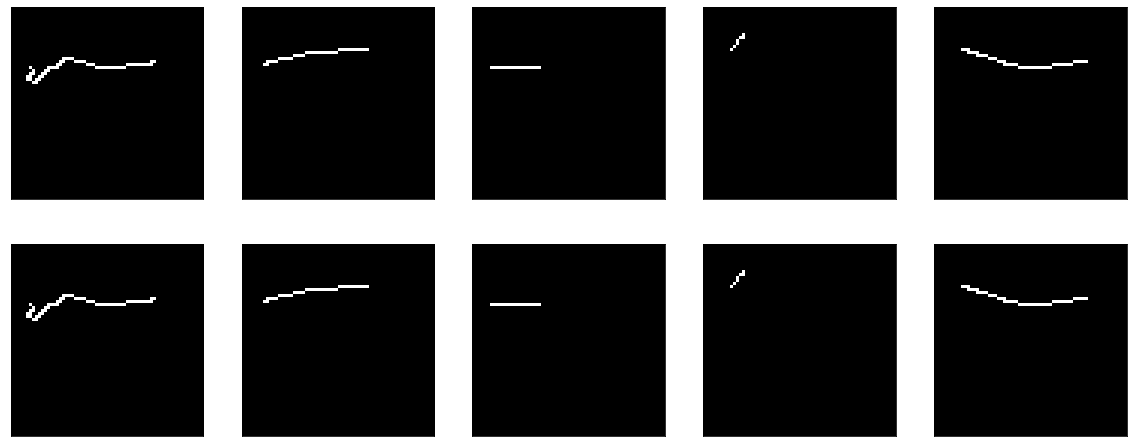
Pero si comienzas a entrenar, entonces comienza, a primera vista, sorprendentemente: el modelo comienza con una precisión == 1.0, pero cae rápidamente.
Evalúe el resultado antes del entrenamiento: 8/Unknown - 1s 140ms/step - loss: 0.2488 - accuracy: 1.0000[0.24875330179929733, 1.0] . Entrenamiento:

 Epoch 1/20 100/100 [==============================] - 6s 56ms/step - loss: 0.1589 - accuracy: 0.9990 - val_loss: 0.0944 - val_accuracy: 0.9967 Epoch 2/20 100/100 [==============================] - 5s 51ms/step - loss: 0.0836 - accuracy: 0.9964 - val_loss: 0.0624 - val_accuracy: 0.9958 Epoch 3/20 100/100 [==============================] - 5s 50ms/step - loss: 0.0633 - accuracy: 0.9961 - val_loss: 0.0470 - val_accuracy: 0.9958 Epoch 4/20 100/100 [==============================] - 5s 48ms/step - loss: 0.0520 - accuracy: 0.9961 - val_loss: 0.0423 - val_accuracy: 0.9961 Epoch 5/20 100/100 [==============================] - 5s 48ms/step - loss: 0.0457 - accuracy: 0.9962 - val_loss: 0.0357 - val_accuracy: 0.9962 

Sí, y no está muy claro, ya tenemos un modelo ideal: la imagen sale 1 en 1 y la pérdida (error cuadrático medio) muestra casi 0,25.

Esto, por cierto, es una pregunta frecuente en los foros: la pérdida está disminuyendo, pero la precisión no está creciendo, ¿cómo puede ser?
Aquí vale la pena recordar una vez más la definición de la capa Densa: output = activation(dot(input, kernel) + bias) y la palabra activación mencionada en ella, que ignoré con éxito anteriormente. Con pesos de la matriz de identidad y sin sesgo, obtenemos output = activation(input) .

En realidad, la función de activación en nuestro código fuente ya está indicada, sigmoide, la copié bastante estúpidamente y eso es todo. Y en los tutoriales se recomienda usarlo en todas partes. Pero tienes que resolverlo.

Para empezar, puede leer en la documentación lo que escriben al respecto: The sigmoid activation: (1.0 / (1.0 + exp(-x))) . Eso personalmente no me dice nada, porque no soy fantasma una vez para construir tales gráficos en mi cabeza.
Pero puedes construir con bolígrafos:

 import matplotlib.ticker as plticker range_tensor = tf.range(-4, 4, 0.01, dtype=tf.float32) fig, ax = plt.subplots(1,1) plt.plot(range_tensor.numpy(), tf.keras.activations.sigmoid(range_tensor).numpy()) ax.grid(which='major', linestyle='-', linewidth='0.5', color='red') ax.grid(which='minor', linestyle=':', linewidth='0.5', color='black') ax.yaxis.set_major_locator(plticker.MultipleLocator(base=0.5) ) plt.minorticks_on() 

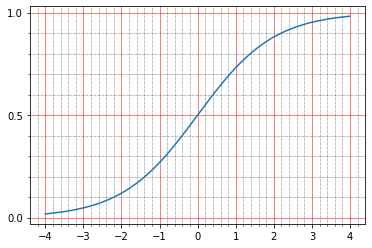
Y aquí queda claro que en cero el sigmoide toma el valor 0.5 y en la unidad, alrededor de 0.73. Y los puntos que tenemos son negros (0.0) o blancos (1.0). Por lo tanto, resulta que el error cuadrático medio de la función de identidad no es cero.

Incluso puedes mirar los bolígrafos, aquí hay una línea de la imagen resultante:

 array([0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.7310586, 0.7310586, 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 ], dtype=float32) 

Y eso es todo, de hecho, muy bueno, porque aparecen varias preguntas a la vez:

• ¿Por qué esto no era visible en la visualización anterior?
• ¿Por qué entonces precisión == 1.0, porque las imágenes originales son 0 y 1.

Con la visualización, todo es sorprendentemente simple. Para mostrar las imágenes, utilicé matplotlib: plt.imshow(res_imgs[i][:, :, 0]) . Y, como de costumbre, si va a la documentación, todo se escribirá allí: The Normalize instance used to scale scalar data to the [0, 1] range before mapping to colors using cmap. By default, a linear scaling mapping the lowest value to 0 and the highest to 1 is used. The Normalize instance used to scale scalar data to the [0, 1] range before mapping to colors using cmap. By default, a linear scaling mapping the lowest value to 0 and the highest to 1 is used. Es decir la biblioteca normalizó cuidadosamente mi 0.5 y 0.73 en el rango de 0 a 1. Cambie el código:

 plt.imshow(res_imgs[i][:, :, 0], norm=matplotlib.colors.Normalize(0.0, 1.0)) 

Y aquí está la pregunta con precisión. Para empezar, por costumbre, vamos a la documentación, leemos tf.keras.metrics.Accuracy y allí parece que escriben comprensible:

 For example, if y_true is [1, 2, 3, 4] and y_pred is [0, 2, 3, 4] then the accuracy is 3/4 or .75. 

Pero en este caso, nuestra precisión debería haber sido 0. Yo, como resultado, me enterré en la fuente y es bastante claro para mí:

  When you pass the strings 'accuracy' or 'acc', we convert this to one of `tf.keras.metrics.BinaryAccuracy`, `tf.keras.metrics.CategoricalAccuracy`, `tf.keras.metrics.SparseCategoricalAccuracy` based on the loss function used and the model output shape. We do a similar conversion for the strings 'crossentropy' and 'ce' as well. 

Además, en la documentación del sitio, por alguna razón, este párrafo no se encuentra en la descripción de .compile .

Aquí hay un fragmento de código de https://github.com/tensorflow/tensorflow/blob/66c48046f169f3565d12e5fea263f6d731f9bfd2/tensorflow/python/keras/engine/compile_utils.py

 y_t_rank = len(y_t.shape.as_list()) y_p_rank = len(y_p.shape.as_list()) y_t_last_dim = y_t.shape.as_list()[-1] y_p_last_dim = y_p.shape.as_list()[-1] is_binary = y_p_last_dim == 1 is_sparse_categorical = ( y_t_rank < y_p_rank or y_t_last_dim == 1 and y_p_last_dim > 1) if metric in ['accuracy', 'acc']: if is_binary: metric_obj = metrics_mod.binary_accuracy elif is_sparse_categorical: metric_obj = metrics_mod.sparse_categorical_accuracy else: metric_obj = metrics_mod.categorical_accuracy 

y_t es y_true, o la salida esperada, y_p es y_predicted, o el resultado predicho.
Tenemos el formato de datos: shape=(64,64,1) , por lo que resulta que la precisión se considera como binary_accuracy. Interés por el bien de cómo se considera:

 def binary_accuracy(y_true, y_pred, threshold=0.5): threshold = math_ops.cast(threshold, y_pred.dtype) y_pred = math_ops.cast(y_pred > threshold, y_pred.dtype) return K.mean(math_ops.equal(y_true, y_pred), axis=-1) 

Es curioso que aquí tengamos suerte: por defecto, todo se considera una unidad que es más de 0.5, y 0.5 y menos - cero. Entonces, la precisión es cien por ciento para nuestro modelo de identidad, aunque en realidad los números no son iguales. Bueno, está claro que si realmente queremos, entonces podemos corregir el umbral y reducir la precisión a cero, por ejemplo, solo que no es realmente necesario. Esta es una métrica, no afecta la capacitación, solo necesita comprender que puede calcularla de mil maneras diferentes y obtener indicadores completamente diferentes. Solo como ejemplo, puede extraer varias métricas con bolígrafos y transferirles nuestros datos:

 m = tf.keras.metrics.BinaryAccuracy() m.update_state(x_batch, res_imgs) print(m.result().numpy()) 

Nos dará 1.0 .

Y aqui

 m = tf.keras.metrics.Accuracy() m.update_state(x_batch, res_imgs) print(m.result().numpy()) 

Nos dará 0.0 en los mismos datos.

Por cierto, se puede usar el mismo código para jugar con funciones de pérdida y comprender cómo funcionan. Si lees los tutoriales en codificadores automáticos, entonces básicamente sugieren usar una de las dos funciones de pérdida: error cuadrático medio o 'binary_crossentropy'. También puedes mirarlos al mismo tiempo.

Les recuerdo que por mi parte ya di modelos de evaluate :

 8/Unknown - 2s 221ms/step - loss: 0.2488 - accuracy: 1.0000[0.24876083992421627, 1.0] 

Es decir pérdida == 0.2488. Veamos por qué es esto. Personalmente, me parece que es el más simple y más comprensible: la diferencia entre y_true y y_predict se resta píxel por píxel, cada resultado se eleva al cuadrado y luego se busca el promedio.

 tf.keras.backend.mean(tf.math.squared_difference(x_batch[0], res_imgs[0])) 

Y a la salida:

 <tf.Tensor: shape=(), dtype=float32, numpy=0.24826494> 

Aquí la intuición es muy simple: la mayoría de los píxeles vacíos, el modelo produce 0.5, obtienen 0.25 - diferencia al cuadrado para ellos.

Con la crossenttrtopy binaria, las cosas son un poco más complicadas, y hay artículos completos sobre cómo funciona esto, pero personalmente siempre fue más fácil para mí leer las fuentes, y ahí parece algo así:

  if from_logits: return nn.sigmoid_cross_entropy_with_logits(labels=target, logits=output) if not isinstance(output, (ops.EagerTensor, variables_module.Variable)): output = _backtrack_identity(output) if output.op.type == 'Sigmoid': # When sigmoid activation function is used for output operation, we # use logits from the sigmoid function directly to compute loss in order # to prevent collapsing zero when training. assert len(output.op.inputs) == 1 output = output.op.inputs[0] return nn.sigmoid_cross_entropy_with_logits(labels=target, logits=output) # Compute cross entropy from probabilities. bce = target * math_ops.log(output + epsilon()) bce += (1 - target) * math_ops.log(1 - output + epsilon()) return -bce 

Para ser honesto, me dediqué el cerebro a estas pocas líneas de código durante mucho tiempo. En primer lugar, queda claro de inmediato que dos implementaciones pueden funcionar: se sigmoid_cross_entropy_with_logits a sigmoid_cross_entropy_with_logits o funcionará el último par de líneas. La diferencia es que sigmoid_cross_entropy_with_logits funciona con logits (como su nombre lo indica, doh), y el código principal funciona con probabilidades.

¿Quiénes son los logits? Si lees un millón de artículos diferentes sobre el tema, entonces mencionarán definiciones matemáticas, fórmulas, algo más. En la práctica, todo parece sorprendentemente simple (corrígeme si me equivoco). El resultado bruto de la predicción es logits. Bueno, o log-odds, las probabilidades logarítmicas que se miden en log istic un its - logistic loros.

 ln(1/2) == -0.69 ln(2/1) == 0.69 ln(1/100) == -4.6 ln(100/1) == 4.6 

En el caso de tensorflow, esto es bastante arbitrario, porque, estrictamente hablando, la salida de la capa no es matemáticamente log-odds, pero se acepta. Si el valor bruto es de -∞ a + ∞, entonces logits. Entonces se pueden convertir en probabilidades. Hay dos opciones para esto: softmax y su caso especial, sigmoide. Softmax: tome un vector de logits y conviértalos en un vector de probabilidades, y aun así la suma de la probabilidad de todos los eventos en él resulta ser 1. Sigmoid (en el caso de tf) también toma un vector de logits, pero convierte cada uno de ellos en probabilidades por separado, independientemente del resto

 # 1+ln(0.5) == 0.30685281944 tf.math.softmax(tf.constant([0.30685281944, 1.0, 0.30685281944])) ## <tf.Tensor: shape=(3,), dtype=float32, numpy=array([0.25, 0.5 , 0.25], dtype=float32)> tf.math.sigmoid(tf.constant([0.30685281944, 1.0, 0.30685281944])) ## <tf.Tensor: shape=(3,), dtype=float32, numpy=array([0.57611686, 0.7310586 , 0.57611686], dtype=float32)> 

Puedes verlo de esta manera. Hay tareas de clasificación de etiquetas múltiples, hay tareas de clasificación de clases múltiples. Multiclase: esto es si necesita determinar las manzanas en la imagen o las naranjas, y tal vez incluso las piñas. Y multilabel es cuando puede haber un jarrón de frutas en la imagen y hay que decir que tiene manzanas y naranjas, pero no hay piñas. Si queremos multiclase, necesitamos softmax, si queremos multilabel, necesitamos sigmoide.
Aquí tenemos el caso de multilabel: es necesario que cada píxel (clase) individual indique si está instalado.

Volviendo al flujo de tensor y por qué en la crossentropía binaria (al menos en otras funciones de crossentropía es casi lo mismo) hay dos ramas globales. La crossentropía siempre funciona con probabilidades, hablaremos de esto un poco más tarde. Luego, hay simplemente dos formas: las probabilidades ya ingresan a la entrada o los logits llegan a la entrada, y luego se les aplica sigmoide para obtener la probabilidad. Dio la casualidad de que aplicar sigmoide y calcular la entropía cruzada resultó ser mejor que simplemente calcular la entropía cruzada a partir de las probabilidades (la fuente de la función sigmoid_cross_entropy_with_logits tiene una conclusión matemática, más para los curiosos que pueden buscar en google 'entropía cruzada de estabilidad numérica'), por lo tanto, incluso los desarrolladores de tensorflow recomiendan no pasar la probabilidad a ingrese funciones de crossentropía y devuelva logits sin procesar. Bueno, justo en el código, las funciones de pérdida se verifican si la última capa es sigmoidea, luego la cortarán y tomarán la entrada de activación, en lugar de su salida, para calcular, enviando todo para ser considerado en sigmoid_cross_entropy_with_logits .

Bien, lo solucioné, ahora binary_crossentropy. Hay dos explicaciones "intuitivas" populares que miden la entropía cruzada.

Más formal: imagine que hay un cierto modelo que para n clases conoce la probabilidad de su ocurrencia (y ₀ , y ₁ , ..., y _n ). Y ahora en la vida, cada una de estas clases ha surgido k _n veces (k ₁ , k ₁ , ..., k _n ). La probabilidad de tal evento es el producto de la probabilidad para cada clase individual - (y ₁ ^ k ₁ ) (y ₂ ^ k ₂ ) ... (y _n ^ k _n ). En principio, esta es una definición normal de entropía cruzada, la probabilidad de un conjunto de datos se expresa en términos de la probabilidad de otro conjunto de datos. El problema con esta definición es que resultará ser de 0 a 1 y, a menudo, será muy pequeño; no es conveniente comparar tales valores.
Si tomamos el logaritmo de esto, entonces k ₁ log (y ₁ ) + k ₂ log (y ₂ ) saldrá y así sucesivamente. El rango de valores pasa de -∞ a 0. Multiplica todo esto por -1 / n - y el rango de 0 a + ∞ sale, además, porque se expresa como la suma de los valores para cada clase, el cambio en cada clase se refleja en el valor general de una manera muy predecible.

Más simple: la entropía cruzada muestra cuántos bits adicionales se necesitan para expresar la muestra en términos del modelo original. Si estuviéramos allí para hacer un logaritmo con base 2, entonces iríamos directamente a bits. Utilizamos logaritmos naturales en todas partes, por lo que muestran el número de nat ( https://en.wikipedia.org/wiki/Nat_(unit )), no bits.

La entropía cruzada binaria, a su vez, es un caso especial de entropía cruzada ordinaria, cuando el número de clases es dos. Entonces tenemos suficiente conocimiento de la probabilidad de ocurrencia de una clase - y ₁ , y la probabilidad de ocurrencia de la segunda será (1-y ₁ ).

Pero, me parece, me resbaló un poco. Permítame recordarle que la última vez que intentamos construir un codificador automático de identidad, nos mostró una imagen hermosa e incluso una precisión de 1.0, pero en realidad los números resultaron ser horribles. Por el bien del experimento, puede realizar un par de pruebas más:
1) la activación se puede eliminar por completo, habrá una identidad limpia
2) puede probar otras funciones de activación, por ejemplo, el mismo relu

Sin activación:

 model = tf.keras.Sequential() model.add(tf.keras.Input(shape=(64,64,1))) model.add(tf.keras.layers.Flatten()) model.add(tf.keras.layers.Dense(64*64, use_bias=False, kernel_initializer=tf.keras.initializers.Identity())) model.add(tf.keras.layers.Reshape(target_shape=(64,64,1))) 

Obtenemos el modelo de identidad perfecto:

 model.evaluate(x=val.map(lambda x: (x,x)).batch(BATCH_SIZE, drop_remainder=True)) # 8/Unknown - 1s 173ms/step - loss: 0.0000e+00 - accuracy: 1.0000[0.0, 1.0] 

El entrenamiento, por cierto, no conducirá a nada, porque la pérdida == 0.0.

Ahora con relu. Su gráfico se ve así:

 import matplotlib.ticker as plticker range_tensor = tf.range(-4, 4, 0.01, dtype=tf.float32) fig, ax = plt.subplots(1,1) plt.plot(range_tensor.numpy(), tf.keras.activations.relu(range_tensor).numpy()) ax.grid(which='major', linestyle='-', linewidth='0.5', color='red') ax.grid(which='minor', linestyle=':', linewidth='0.5', color='black') ax.yaxis.set_major_locator(plticker.MultipleLocator(base=1) ) plt.minorticks_on() 

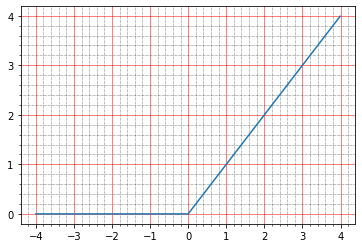
Por debajo de cero - cero, por encima - y = x, es decir en teoría, deberíamos obtener el mismo efecto que en ausencia de activación, un modelo ideal.

 model = tf.keras.Sequential() model.add(tf.keras.Input(shape=(64,64,1))) model.add(tf.keras.layers.Flatten()) model.add(tf.keras.layers.Dense(64*64, activation='relu', use_bias=False, kernel_initializer=tf.keras.initializers.Identity())) model.add(tf.keras.layers.Reshape(target_shape=(64,64,1))) model.compile(optimizer="adam", loss="binary_crossentropy", metrics=["accuracy"]) model.evaluate(x=val.map(lambda x: (x,x)).batch(BATCH_SIZE, drop_remainder=True)) # 8/Unknown - 1s 158ms/step - loss: 0.0000e+00 - accuracy: 1.0000[0.0, 1.0] 

De acuerdo, descubrimos el modelo de identidad, incluso con alguna parte de la teoría se hizo más claro. Ahora intentemos entrenar el mismo modelo para que se convierta en identidad.

Por diversión, realizaré este experimento con tres funciones de activación. Para empezar, relu, porque se mostró mucho antes (todo es como antes, pero el kernel_initializer se elimina, por lo que por defecto será glorot_uniform ):

 model = tf.keras.Sequential() model.add(tf.keras.Input(shape=(64,64,1))) model.add(tf.keras.layers.Flatten()) model.add(tf.keras.layers.Dense(64*64, activation='relu', use_bias=False)) model.add(tf.keras.layers.Reshape(target_shape=(64,64,1))) 

Aprende maravillosamente:

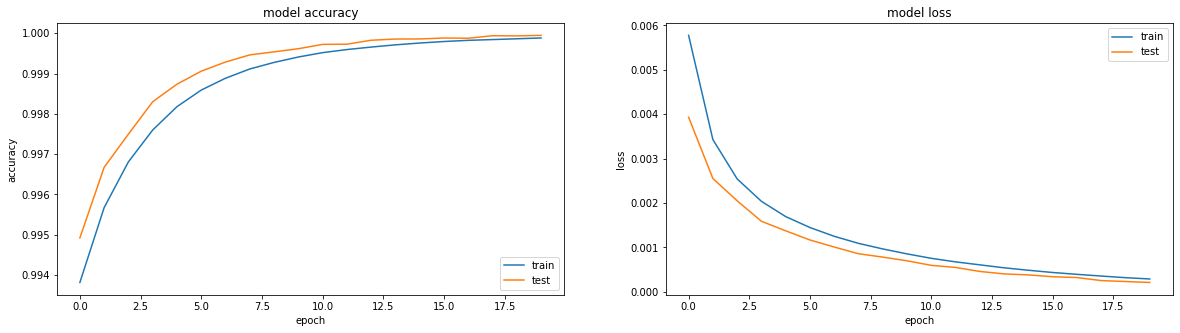
El resultado fue bastante bueno, precisión: 0.9999, pérdida (ms): 2e-04 después de 20 eras y puede entrenar más.

A continuación, intente con sigmoide:

 model = tf.keras.Sequential() model.add(tf.keras.Input(shape=(64,64,1))) model.add(tf.keras.layers.Flatten()) model.add(tf.keras.layers.Dense(64*64, activation='sigmoid', use_bias=False)) model.add(tf.keras.layers.Reshape(target_shape=(64,64,1))) 

Ya enseñé algo similar antes, con la única diferencia de que el sesgo está deshabilitado aquí. Él estudia humildemente, va a una meseta en la región de la era 50, precisión: 0.9970, pérdida: 0.01 después de 60 eras.

El resultado nuevamente no es impresionante:

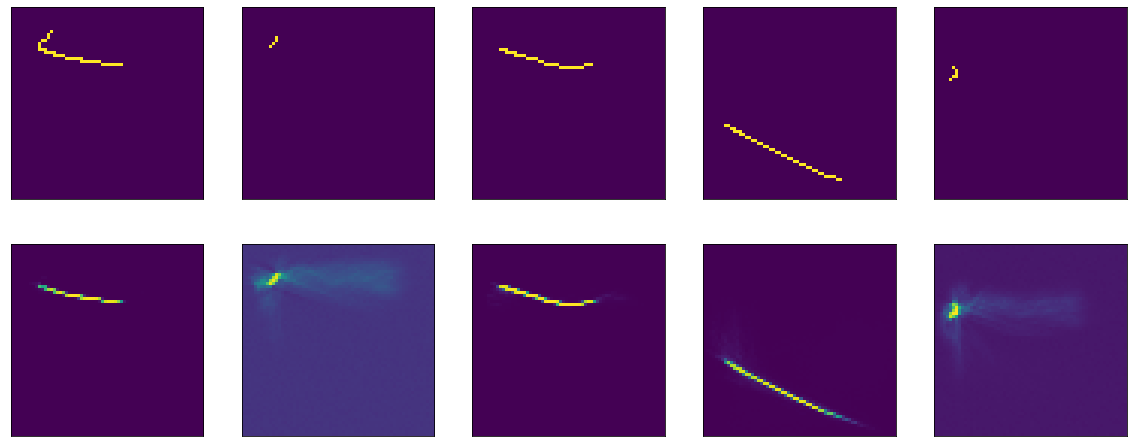
Bueno, también verifique tanh:

 model = tf.keras.Sequential() model.add(tf.keras.Input(shape=(64,64,1))) model.add(tf.keras.layers.Flatten()) model.add(tf.keras.layers.Dense(64*64, activation='tanh', use_bias=False)) model.add(tf.keras.layers.Reshape(target_shape=(64,64,1))) 

El resultado es comparable a relu - precisión: 0.9999, pérdida: 6e-04 después de 20 eras, y puede entrenar más:

De hecho, me atormenta la cuestión de si se puede hacer algo para que el sigmoide muestre un resultado comparable. Exclusivamente por interés deportivo.

Por ejemplo, puede intentar agregar BatchNormalization:

 model = tf.keras.Sequential() model.add(tf.keras.Input(shape=(64,64,1))) model.add(tf.keras.layers.Flatten()) model.add(tf.keras.layers.Dense(64*64, activation='sigmoid', use_bias=False)) model.add(tf.keras.layers.BatchNormalization()) model.add(tf.keras.layers.Reshape(target_shape=(64,64,1))) 

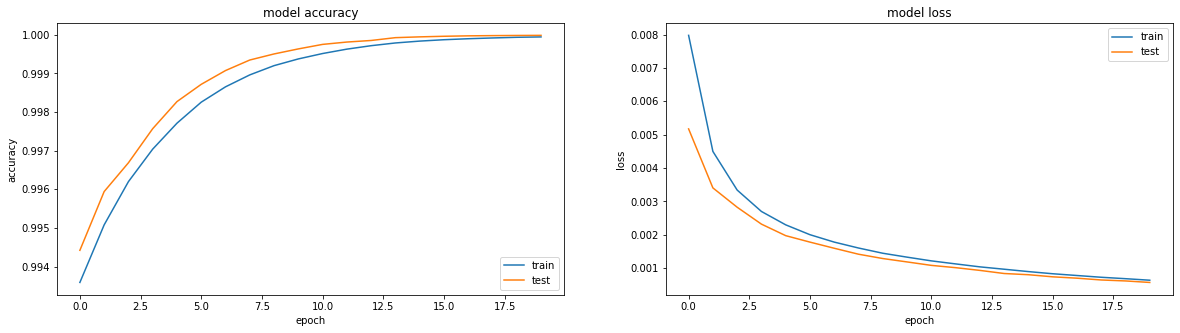
Y luego ocurre algún tipo de magia. En la decimotercera era, precisión: 1.0. Y los resultados ardientes:

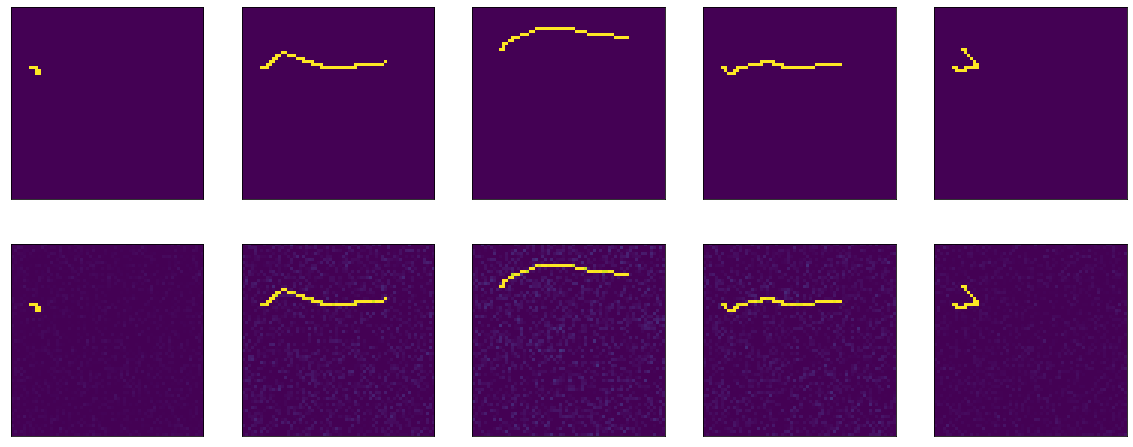
III ... en este colgador de acantilados terminaré la primera parte, porque el texto es demasiado aburrido, y no está claro si alguien lo necesita o no. En la segunda parte, entenderé qué sucedió la magia, experimentaré con diferentes optimizadores, trataré de construir un codificador-decodificador honesto, golpearé mi cabeza sobre la mesa. Espero que alguien haya estado interesado y servicial.