Esta es la segunda parte del artículo sobre numba. El primero fue una introducción histórica y un breve manual de instrucciones de numba. Aquí presento un código de tarea ligeramente modificado del artículo de Haskell " Más rápido que C ++; más lento que PHP "(compara el rendimiento de las implementaciones de un algoritmo en diferentes lenguajes / compiladores) con puntos de referencia, gráficos y explicaciones más detallados. Diré de inmediato que vi el artículo Oh, este C / C ++ lento y, muy probablemente, si realiza estos cambios en el código C, la imagen cambiará un poco, pero incluso en este caso, la pitón puede superar la velocidad de C incluso en esta versión Es en sí notable.

Se reemplazó la lista de Python con una matriz numpy (y, en consecuencia, v0[:] con v0.copy() , porque en numpy a[:] devuelve la view lugar de copiar).
Para comprender la naturaleza del comportamiento de rendimiento, realicé un "escaneo" por la cantidad de elementos en la matriz.
En el código de Python, reemplacé time.monotonic con time.perf_counter , ya que es más preciso (1us versus 1ms para monotonic).
Como numba usa la compilación jit, esta compilación debería tener lugar algún día. Por defecto, ocurre la primera vez que se llama a la función e inevitablemente afecta los resultados de los puntos de referencia (aunque si se toma el tiempo de tres lanzamientos, es posible que no lo note), y también se siente en el uso práctico. Hay varias formas de lidiar con este fenómeno:
1) resultados de la compilación de caché en el disco:
@njit(cache=True) def lev_dist(s1: AnyStr, s2: AnyStr) -> int:
luego se realizará la compilación en la primera llamada del programa, y en las llamadas posteriores se extraerá del disco.
2) indicar la firma
La compilación ocurrirá en el momento en que Python analiza la definición de la función, y el primer inicio ya será rápido.
La cadena original se transmite (más precisamente, bytes), pero recientemente se ha agregado soporte para cadenas, por lo que la firma es bastante monstruosa (ver más abajo). Las firmas generalmente se escriben de manera más simple:
@njit(nb.int64(nb.uint8[:], nb.uint8[:])) def lev_dist(s1, s2):
pero luego debes convertir bytes a una matriz numpy por adelantado:
s1_py = [int(x) for x in b"a" * 15000] s1 = np.array(s1_py, dtype=np.uint8)
o
s1 = np.full(15000, ord('a'), dtype=np.uint8)
Y puede dejar los bytes como están y especificar la firma en este formulario:
@njit(nb.int64(nb.bytes(nb.uint8, nb.1d, nb.C), nb.bytes(nb.uint8, nb.1d, nb.C))) def lev_dist(s1: AnyStr, s2: AnyStr) -> int:
La velocidad de ejecución para los bytes y la matriz numpy de uint8 (en este caso) es la misma.
3) precalentar el caché
s1 = b"a" * 15
Entonces la compilación se producirá en la primera llamada, y la segunda ya será rápida.
Código C (clang -O3 -march = native) #include <stdio.h> #include <stdlib.h> #include <string.h> #include <time.h> static long lev_dist (const char *s1, unsigned long m, const char *s2, unsigned long n) { // unsigned long m, n; unsigned long i, j; long *v0, *v1; long ret, *temp; /* Edge cases. */ if (m == 0) { return n; } else if (n == 0) { return m; } v0 = malloc (sizeof (long) * (n + 1)); v1 = malloc (sizeof (long) * (n + 1)); if (v0 == NULL || v1 == NULL) { fprintf (stderr, "failed to allocate memory\n"); exit (-1); } for (i = 0; i <= n; ++i) { v0[i] = i; } memcpy (v1, v0, sizeof(long) * (n + 1)); for (i = 0; i < m; ++i) { v1[0] = i + 1; for (j = 0; j < n; ++j) { const long subst_cost = (s1[i] == s2[j]) ? v0[j] : (v0[j] + 1); const long del_cost = v0[j + 1] + 1; const long ins_cost = v1[j] + 1; #if !defined(__GNUC__) || defined(__llvm__) if (subst_cost < del_cost) { v1[j + 1] = subst_cost; } else { v1[j + 1] = del_cost; } #else v1[j + 1] = (subst_cost < del_cost) ? subst_cost : del_cost; #endif if (ins_cost < v1[j + 1]) { v1[j + 1] = ins_cost; } } temp = v0; v0 = v1; v1 = temp; } ret = v0[n]; free (v0); free (v1); return ret; } int main () { char s1[25001], s2[25001], s3[25001]; int lengths[] = {1000, 2000, 5000, 10000, 15000, 20000, 25000}; FILE *fout; fopen_s(&fout, "c.txt", "w"); for(int j = 0; j < sizeof(lengths)/sizeof(lengths[0]); j++){ int len = lengths[j]; int i; clock_t start_time, exec_time; for (i = 0; i < len; ++i) { s1[i] = 'a'; s2[i] = 'a'; s3[i] = 'b'; } s1[len] = s2[len] = s3[len] = '\0'; start_time = clock (); printf ("%ld\n", lev_dist (s1, len, s2, len)); printf ("%ld\n", lev_dist (s1, len, s3, len)); exec_time = clock () - start_time; fprintf(fout, "%d %.6f\n", len, ((double) exec_time) / CLOCKS_PER_SEC); fprintf (stderr, "Finished in %.3fs\n", ((double) exec_time) / CLOCKS_PER_SEC); } return 0; }
La comparación se realizó bajo windows (windows 10 x64, python 3.7.3, numba 0.45.1, clang 9.0.0, intel m5-6y54 skylake): y bajo linux (debian 4.9.30, python 3.7.4, numba 0.45.1, Clang 9.0.0).
X es el tamaño de la matriz, y es el tiempo en segundos.
Escala lineal de Windows:
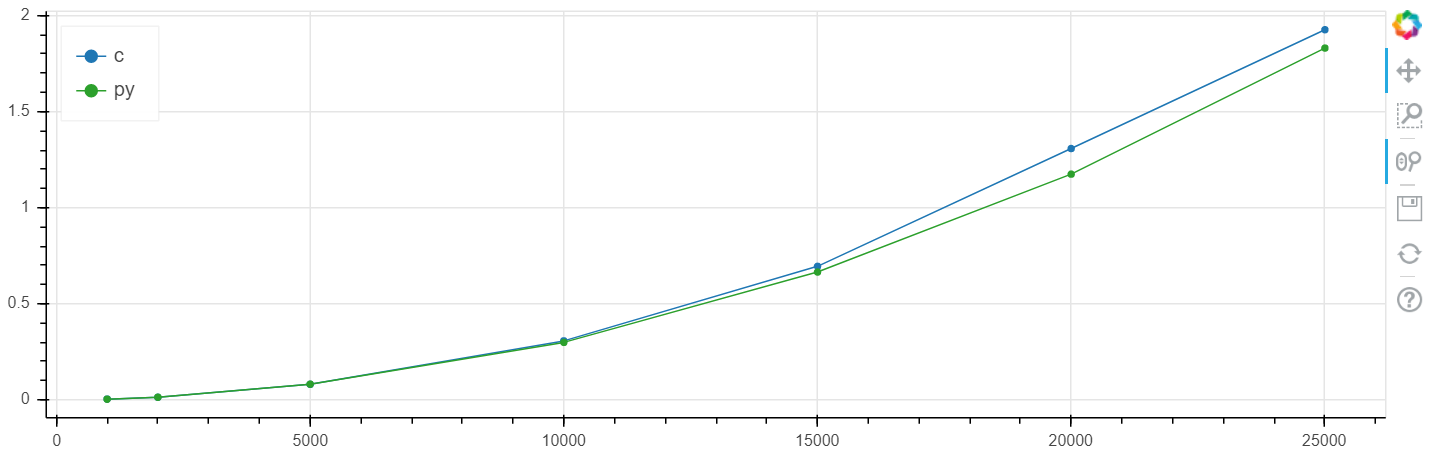
Escala logarítmica de Windows:
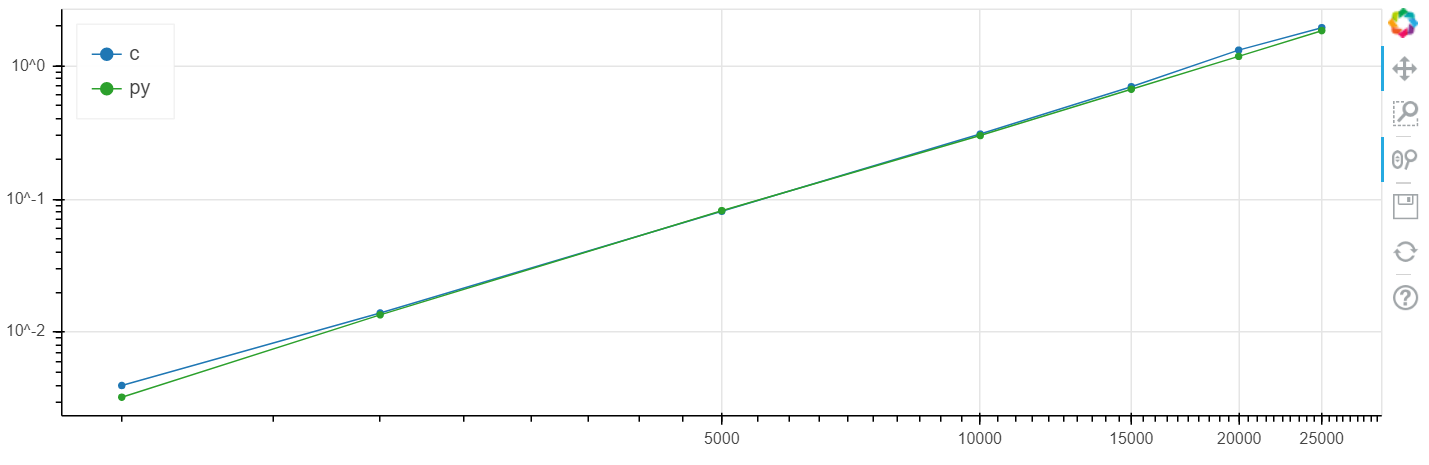
Escala lineal de Linux:

Escala logarítmica de Linux
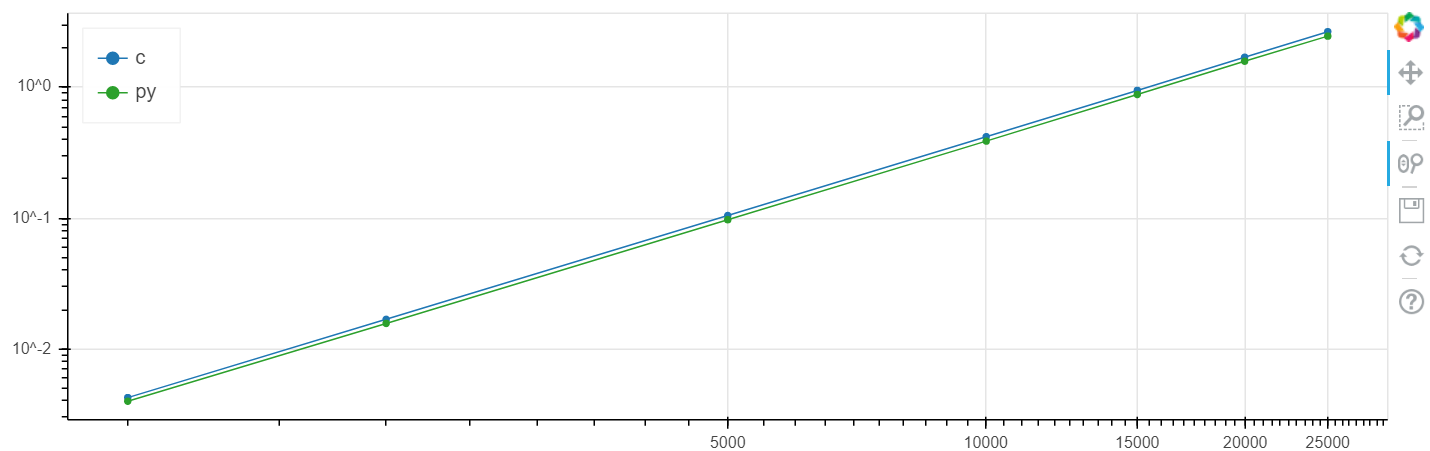
En este problema, se obtuvo un aumento en la velocidad en comparación con el ruido metálico a un nivel de varios por ciento, que generalmente es más alto que el error estadístico.
Repetidamente hice esta comparación en diferentes tareas y, como regla, si numba puede acelerar algo, lo acelera a una velocidad dentro del margen de error que coincide con la velocidad C (sin usar insertos de ensamblador).
Repito que si realiza cambios en el código en C desde Oh, esta situación lenta de C / C ++ puede cambiar.
Estaré encantado de escuchar preguntas y sugerencias en los comentarios.
PD Al especificar la firma de las matrices, es mejor establecer explícitamente la forma de alternar filas / columnas:
para que numba no piense en 'C' (si) esto o 'A' (reconocimiento automático si / fortran), por alguna razón esto afecta el rendimiento incluso para matrices unidimensionales, para esto existe una sintaxis tan original: uint8[:,:] esto ' A '(detección automática), nb.uint8[:, ::1] es' C '(si), np.uint8[::1, :] es' F '(fortran).
@njit(nb.int64(nb.uint8[::1], nb.uint8[::1])) def lev_dist(s1, s2):