SVM Explicación desde cero e implementación en python. Análisis detallado del método del vector de soporte.

¡Hola a todos los que eligieron el camino de ML-Samurai!

Introducción

En este artículo, consideramos el método de máquina de vectores de soporte ( Eng. SVM, Support Vector Machine ) para el problema de clasificación. Se presentará la idea principal del algoritmo, se analizará el resultado de establecer sus pesos y una implementación de bricolaje simple. En el ejemplo de un conjunto de datos $$$Iris$ Se demostrará el funcionamiento del algoritmo escrito con datos separables / inseparables linealmente en el espacio. $$$R ^ 2$ y visualización de entrenamiento / pronóstico. Además, se anunciarán los pros y los contras del algoritmo, sus modificaciones.

Figura 1. Foto de código abierto de una flor de iris

El problema a resolver:

Resolveremos el problema de la clasificación binaria (cuando solo hay dos clases). Primero, el algoritmo se entrena en objetos del conjunto de entrenamiento, para el cual las etiquetas de clase se conocen de antemano. Además, el algoritmo ya entrenado predice la etiqueta de clase para cada objeto de la muestra diferida / de prueba. Las etiquetas de clase pueden tomar valores $$$Y = \ {- 1, +1 \}$ . Objeto - vector con signos N $$$x = (x_1, x_2, ..., x_n)$ en el espacio $$$R ^ n$ . Al aprender, el algoritmo debe construir una función $$$F (x) = y$ que toma un argumento $$$x$ - un objeto del espacio $$$R ^ n$ y le da la etiqueta de clase $$$y$ .

Palabras generales sobre el algoritmo:

La tarea de clasificación se relaciona con la enseñanza con un maestro. SVM es un algoritmo de aprendizaje con un profesor. Visualmente, se pueden encontrar muchos algoritmos de aprendizaje automático en este artículo de primer nivel (consulte la sección "Mapa del mundo del aprendizaje automático"). Cabe agregar que SVM también se puede usar para problemas de regresión, pero el clasificador SVM se analizará en este artículo.

El objetivo principal de SVM como clasificador es encontrar la ecuación de un hiperplano de separación
$$$w_1x_1 + w_2x_2 + ... + w_nx_n + w_0 = 0$ en el espacio $$$R ^ n$ , que dividiría las dos clases de una manera óptima. Vista general de la transformación. $$$F$ facilidad $$$x$ a la etiqueta de clase $$$Y$ : $$$F (x) = signo (w ^ Tx-b)$ . Recordaremos que hemos designado $$$w = (w_1, w_2, ..., w_n), b = -w_0$ . Después de configurar los pesos del algoritmo $$$w$ y $$$b$ (entrenamiento), todos los objetos que caen en un lado del hiperplano construido se predecirán como la primera clase, y los objetos que caen en el otro lado, la segunda clase.

Función interior $$$signo ()$ Existe una combinación lineal de características del objeto con los pesos del algoritmo, por lo que SVM se refiere a algoritmos lineales. Un hiperplano divisor se puede construir de diferentes maneras, pero en pesos SVM $$$w$ y $$$b$ están configurados para que los objetos de clase se encuentren lo más lejos posible del hiperplano de separación. En otras palabras, el algoritmo maximiza la brecha ( margen inglés ) entre el hiperplano y los objetos de clase que están más cerca de él. Dichos objetos se denominan vectores de soporte (ver Fig. 2). De ahí el nombre del algoritmo.

Figura 2. SVM (la base de la figura de aquí )

Una salida detallada de las reglas de ajuste de escala SVM:

Para mantener el hiperplano divisor lo más lejos posible de los puntos de muestra, el ancho de la tira debe ser máximo. Vector $$$w$ Es el vector director del hiperplano divisor. En lo sucesivo, denotamos el producto escalar de dos vectores como $$$\ langle a, b \ rangle$ o $$$a ^ Tb$ . Busquemos la proyección del vector cuyos extremos serán los vectores de soporte de diferentes clases en el vector de dirección del hiperplano. Esta proyección mostrará el ancho de la tira divisoria (ver Fig. 3):

Figura 3. La salida de las reglas para establecer las escalas (la base de la figura de aquí )

El margen del objeto x desde el límite de la clase es el valor $$$M = y (w ^ Tx-b)$ . El algoritmo comete un error en el objeto si y solo si la sangría $$$M$ negativo (cuando $$$y$ y $$$(w ^ Tx-b)$ diferentes personajes) Si $$$M ∈ (0, 1)$ , entonces el objeto cae dentro de la franja divisoria. Si $$$M> 1$ , entonces el objeto x se clasifica correctamente y se encuentra a cierta distancia de la franja divisoria. Anotamos esta conexión:

El sistema resultante es la configuración SVM predeterminada con SVM de margen duro , cuando no se permite que ningún objeto ingrese a la banda de separación. Se resuelve analíticamente a través del teorema de Kuhn-Tucker. El problema resultante es equivalente al problema dual de encontrar el punto de silla de la función Lagrange.

$$$$ display $$ \ left \ {\ begin {array} {ll} (w ^ Tw) / 2 \ rightarrow min & \ textrm {} \\ y (w ^ Tx-b) \ geqslant 1 & \ textrm {} \ end {array} \ right. $$ display $$

Todo esto es bueno siempre y cuando nuestras clases sean linealmente separables. Para que el algoritmo pueda funcionar con datos inseparables linealmente, transformemos un poco nuestro sistema. Deje que el algoritmo cometa errores en los objetos de entrenamiento, pero al mismo tiempo trate de mantener menos errores. Introducimos un conjunto de variables adicionales. $$$\ xi _i> 0$ caracterizando la magnitud del error en cada objeto $$$x_i$ . Introducimos una penalización por el error total en el funcional minimizado:

$$$$ display $$ \ left \ {\ begin {array} {ll} (w ^ Tw) / 2 + \ alpha \ sum \ xi _i \ rightarrow min & \ textrm {} \\ y (w ^ Tx_i-b) \ geqslant 1 - \ xi _i & \ textrm {} \\ \ xi _i \ geqslant0 & \ textrm {} \ end {array} \ right. $$ display $$

Consideraremos el número de errores de algoritmo (cuando M <0). Llámalo pena . Entonces la penalización para todos los objetos será igual a la cantidad de multas para cada objeto. $$$x_i$ donde $$$[M_i <0]$ - función umbral (ver Fig. 4):

$$$$ display $$ [M_i <0] = \ left \ {\ begin {array} {ll} 1 & \ textrm {if} M_i <0 \\ 0 & \ textrm {if} M_i \ geqslant 0 \ end {array} \ right. $$ display $$

A continuación, hacemos que la penalización sea sensible a la magnitud del error y al mismo tiempo introducimos una penalización por acercar el objeto al límite de la clase:

Al agregar a la expresión de penalización el término $$$\ alpha (w ^ Tw) / 2$ obtenemos la clásica función de pérdida de SVM con espacio libre ( SVM de margen suave ) para un objeto:

$$$Q$ - función de pérdida, también es una función de pérdida. Eso es lo que minimizaremos con la ayuda del descenso de gradiente en la implementación de las manos. Derivamos las reglas para cambiar los pesos, donde $$$\ eta$ - paso de descenso:

$$$$ display $$ \ bigtriangledown Q = \ left \ {\ begin {array} {ll} \ alpha w-yx & \ textrm {if} yw ^ Tx <1 \\ \ alpha w & \ textrm {if} yw ^ Tx \ geqslant 1 \ end {array} \ right. $$ display $$

Posibles preguntas en las entrevistas (basadas en hechos reales):

Después de preguntas generales sobre SVM: ¿Por qué Hinge_loss maximiza el espacio libre? - Primero, recuerde que un hiperplano cambia su posición cuando cambian los pesos $$$w$ y $$$b$ . Los pesos del algoritmo comienzan a cambiar cuando los gradientes de la función de pérdida no son iguales a cero (por lo general dicen: "flujo de gradientes"). Por lo tanto, seleccionamos especialmente dicha función de pérdida, en la que los gradientes comienzan a fluir en el momento adecuado. $$$Pérdida de bisagra$ se ve así: $$$H = max (0,1-y (w ^ Tx))$ . Recuerda que la autorización $$$m = y (w ^ Tx)$ . Cuando la brecha $$$m$ lo suficientemente grande ( $$$1$ o más) expresión $$$(1 m)$ se vuelve menor que cero y $$$H = 0$ (por lo tanto, los gradientes no fluyen y el peso del algoritmo no cambia de ninguna manera). Si la brecha m es suficientemente pequeña (por ejemplo, cuando un objeto cae en la banda de separación y / o negativo (si el pronóstico de clasificación es incorrecto), Hinge_loss se vuelve positivo ( $$$H> 0$ ), los gradientes comienzan a fluir y los pesos del algoritmo cambian. Resumiendo: los gradientes fluyen en dos casos: cuando el objeto de muestra cayó dentro de la banda de separación y cuando el objeto está clasificado incorrectamente.

Para verificar el nivel de un idioma extranjero, son posibles preguntas similares: ¿Cuáles son las similitudes y diferencias entre LogisticRegression y SVM? - En primer lugar, hablaremos de similitudes: ambos algoritmos son algoritmos de clasificación lineal en el aprendizaje supervisado. Algunas similitudes están en sus argumentos de las funciones de pérdida: $$$log (1 + exp (-y (w ^ Tx)))$ para logreg y $$$max (0,1-y (w ^ Tx))$ para SVM (mira la imagen 4). Ambos algoritmos podemos configurarlos usando el descenso de gradiente. A continuación, hablemos de las diferencias: la etiqueta de clase de devolución SVM del objeto a diferencia de LogReg, que devuelve la probabilidad de pertenencia a la clase. SVM no puede funcionar con etiquetas de clase $$$\ {0,1 \}$ (sin renombrar clases) a diferencia de LogReg (FinReg pérdida de pérdida para $$$\ {0,1 \}$ : $$$-ylog (p) - (1-y) log (1-p)$ donde $$$y$ - etiqueta de clase real, $$$p$ - retorno del algoritmo, probabilidad de pertenecer al objeto $$$x$ a clase $$$\ {1 \}$ ) Más que eso, podemos resolver el problema SVM de margen duro sin descenso de gradiente. La tarea de buscar vectores de soporte se reduce al punto de silla de búsqueda en la función Lagrange; esta tarea se refiere únicamente a la programación cuadrática.

import numpy as np import matplotlib.pyplot as plt %matplotlib inline xx = np.linspace(-4,3,100000) plt.plot(xx, [(x<0).astype(int) for x in xx], linewidth=2, label='1 if M<0, else 0') plt.plot(xx, [np.log2(1+2.76**(-x)) for x in xx], linewidth=4, label='logistic = log(1+e^-M)') plt.plot(xx, [np.max(np.array([0,1-x])) for x in xx], linewidth=4, label='hinge = max(0,1-M)') plt.title('Loss = F(Margin)') plt.grid() plt.legend(prop={'size': 14}); 

Figura 4. Funciones de pérdida

Implementación simple de SVM clásico de margen blando:

Atencion Encontrará un enlace al código completo al final del artículo. A continuación hay bloques de código sacados de contexto. Algunos bloques solo pueden iniciarse después de resolver los bloques anteriores. Debajo de muchos bloques, se colocarán imágenes que muestran cómo funciona el código colocado encima.

 import numpy as np import warnings warnings.filterwarnings('ignore') import matplotlib.pyplot as plt import matplotlib.lines as mlines plt.rcParams['figure.figsize'] = (8,6) %matplotlib inline from sklearn.datasets import load_iris from sklearn.decomposition import PCA from sklearn.model_selection import train_test_split def newline(p1, p2, color=None): #    #function kredits to: https://fooobar.com/questions/626491/how-to-draw-a-line-with-matplotlib ax = plt.gca() xmin, xmax = ax.get_xbound() if(p2[0] == p1[0]): xmin = xmax = p1[0] ymin, ymax = ax.get_ybound() else: ymax = p1[1]+(p2[1]-p1[1])/(p2[0]-p1[0])*(xmax-p1[0]) ymin = p1[1]+(p2[1]-p1[1])/(p2[0]-p1[0])*(xmin-p1[0]) l = mlines.Line2D([xmin,xmax], [ymin,ymax], color=color) ax.add_line(l) return l 

 def add_bias_feature(a): a_extended = np.zeros((a.shape[0],a.shape[1]+1)) a_extended[:,:-1] = a a_extended[:,-1] = int(1) return a_extended class CustomSVM(object): __class__ = "CustomSVM" __doc__ = """ This is an implementation of the SVM classification algorithm Note that it works only for binary classification ############################################################# ###################### PARAMETERS ###################### ############################################################# etha: float(default - 0.01) Learning rate, gradient step alpha: float, (default - 0.1) Regularization parameter in 0.5*alpha*||w||^2 epochs: int, (default - 200) Number of epochs of training ############################################################# ############################################################# ############################################################# """ def __init__(self, etha=0.01, alpha=0.1, epochs=200): self._epochs = epochs self._etha = etha self._alpha = alpha self._w = None self.history_w = [] self.train_errors = None self.val_errors = None self.train_loss = None self.val_loss = None def fit(self, X_train, Y_train, X_val, Y_val, verbose=False): #arrays: X; Y =-1,1 if len(set(Y_train)) != 2 or len(set(Y_val)) != 2: raise ValueError("Number of classes in Y is not equal 2!") X_train = add_bias_feature(X_train) X_val = add_bias_feature(X_val) self._w = np.random.normal(loc=0, scale=0.05, size=X_train.shape[1]) self.history_w.append(self._w) train_errors = [] val_errors = [] train_loss_epoch = [] val_loss_epoch = [] for epoch in range(self._epochs): tr_err = 0 val_err = 0 tr_loss = 0 val_loss = 0 for i,x in enumerate(X_train): margin = Y_train[i]*np.dot(self._w,X_train[i]) if margin >= 1: #   self._w = self._w - self._etha*self._alpha*self._w/self._epochs tr_loss += self.soft_margin_loss(X_train[i],Y_train[i]) else: #         0<m<1 self._w = self._w +\ self._etha*(Y_train[i]*X_train[i] - self._alpha*self._w/self._epochs) tr_err += 1 tr_loss += self.soft_margin_loss(X_train[i],Y_train[i]) self.history_w.append(self._w) for i,x in enumerate(X_val): val_loss += self.soft_margin_loss(X_val[i], Y_val[i]) val_err += (Y_val[i]*np.dot(self._w,X_val[i])<1).astype(int) if verbose: print('epoch {}. Errors={}. Mean Hinge_loss={}'\ .format(epoch,err,loss)) train_errors.append(tr_err) val_errors.append(val_err) train_loss_epoch.append(tr_loss) val_loss_epoch.append(val_loss) self.history_w = np.array(self.history_w) self.train_errors = np.array(train_errors) self.val_errors = np.array(val_errors) self.train_loss = np.array(train_loss_epoch) self.val_loss = np.array(val_loss_epoch) def predict(self, X:np.array) -> np.array: y_pred = [] X_extended = add_bias_feature(X) for i in range(len(X_extended)): y_pred.append(np.sign(np.dot(self._w,X_extended[i]))) return np.array(y_pred) def hinge_loss(self, x, y): return max(0,1 - y*np.dot(x, self._w)) def soft_margin_loss(self, x, y): return self.hinge_loss(x,y)+self._alpha*np.dot(self._w, self._w) 

Consideramos en detalle el funcionamiento de cada bloque de líneas:

1) cree una función add_bias_feature (a) , que extiende automáticamente el vector de objetos, agregando el número 1 al final de cada vector, esto es necesario para "olvidarse" del término libre b. Expresión $$$w ^ Tx-b$ equivalente a la expresión $$$w_1x_1 + w_2x_2 + ... + w_nx_n + w_0 * 1$ . Suponemos condicionalmente que la unidad es el último componente del vector para todos los vectores x, y $$$w_0 = -b$ . Ahora configurando los pesos $$$w$ y $$$w_0$ Produciremos al mismo tiempo.

 def add_bias_feature(a): a_extended = np.zeros((a.shape[0],a.shape[1]+1)) a_extended[:,:-1] = a a_extended[:,-1] = int(1) return a_extended 

2) luego describiremos el clasificador mismo. Tiene las funciones de inicializar init () , aprender fit () , predecir predic () , encontrar la pérdida de la función hinge_loss () y encontrar la pérdida total de la función del algoritmo clásico con un espacio suave soft_margin_loss () .

3) tras la inicialización, se introducen 3 hiperparámetros: _etha - paso de descenso de gradiente ( $$$\ eta$ ), _alpha - coeficiente de velocidad de reducción de peso proporcional (antes del término cuadrático en la función de pérdida $$$\ alpha$ ), _epochs - el número de eras de entrenamiento.

  def __init__(self, etha=0.01, alpha=0.1, epochs=200): self._epochs = epochs self._etha = etha self._alpha = alpha self._w = None self.history_w = [] self.train_errors = None self.val_errors = None self.train_loss = None self.val_loss = None 

4) durante el entrenamiento para cada era de la muestra de entrenamiento (X_train, Y_train) tomaremos un elemento de la muestra, calcularemos el espacio entre este elemento y la posición del hiperplano en un momento dado. Además, dependiendo del tamaño de esta brecha, cambiaremos el peso del algoritmo usando el gradiente de la función de pérdida $$$Q$ . Al mismo tiempo, calcularemos el valor de esta función para cada época y cuántas veces cambiamos los pesos por época. Antes de comenzar la capacitación, nos aseguraremos de que no hayan entrado realmente más de dos etiquetas de clase diferentes en la función de aprendizaje. Antes de configurar la balanza, se inicializa utilizando la distribución normal.

  def fit(self, X_train, Y_train, X_val, Y_val, verbose=False): #arrays: X; Y =-1,1 if len(set(Y_train)) != 2 or len(set(Y_val)) != 2: raise ValueError("Number of classes in Y is not equal 2!") X_train = add_bias_feature(X_train) X_val = add_bias_feature(X_val) self._w = np.random.normal(loc=0, scale=0.05, size=X_train.shape[1]) self.history_w.append(self._w) train_errors = [] val_errors = [] train_loss_epoch = [] val_loss_epoch = [] for epoch in range(self._epochs): tr_err = 0 val_err = 0 tr_loss = 0 val_loss = 0 for i,x in enumerate(X_train): margin = Y_train[i]*np.dot(self._w,X_train[i]) if margin >= 1: #   self._w = self._w - self._etha*self._alpha*self._w/self._epochs tr_loss += self.soft_margin_loss(X_train[i],Y_train[i]) else: #         0<m<1 self._w = self._w +\ self._etha*(Y_train[i]*X_train[i] - self._alpha*self._w/self._epochs) tr_err += 1 tr_loss += self.soft_margin_loss(X_train[i],Y_train[i]) self.history_w.append(self._w) for i,x in enumerate(X_val): val_loss += self.soft_margin_loss(X_val[i], Y_val[i]) val_err += (Y_val[i]*np.dot(self._w,X_val[i])<1).astype(int) if verbose: print('epoch {}. Errors={}. Mean Hinge_loss={}'\ .format(epoch,err,loss)) train_errors.append(tr_err) val_errors.append(val_err) train_loss_epoch.append(tr_loss) val_loss_epoch.append(val_loss) self.history_w = np.array(self.history_w) self.train_errors = np.array(train_errors) self.val_errors = np.array(val_errors) self.train_loss = np.array(train_loss_epoch) self.val_loss = np.array(val_loss_epoch) 

Comprobación del funcionamiento del algoritmo escrito:

Verifique que nuestro algoritmo escrito funcione en algún tipo de conjunto de datos de juguetes. Tome el conjunto de datos de Iris. Nosotros prepararemos los datos. Denote las clases 1 y 2 como $$$+ 1$ y clase 0 como $$$-1$ . Usando el algoritmo PCA (explicación y aplicación aquí ), reducimos de manera óptima el espacio de 4 atributos a 2 con una pérdida mínima de datos (nos será más fácil observar el entrenamiento y el resultado). A continuación, nos dividiremos en una muestra de capacitación (entrenamiento) y una demorada (validación). Vamos a entrenar en la muestra de entrenamiento, predecir y verificar el diferido. Elegimos los factores de aprendizaje para que disminuya la función de pérdida. Durante el entrenamiento, veremos la función de pérdida del entrenamiento y el muestreo retrasado.

 #    iris = load_iris() X = iris.data Y = iris.target pca = PCA(n_components=2) X = pca.fit_transform(X) Y = (Y > 0).astype(int)*2-1 # [0,1,2] --> [False,True,True] --> [0,1,1] --> [0,2,2] --> [-1,1,1] X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.4, random_state=2020) 

 #     svm = CustomSVM(etha=0.005, alpha=0.006, epochs=150) svm.fit(X_train, Y_train, X_test, Y_test) print(svm.train_errors) # numbers of error in each epoch print(svm._w) # w0*x_i[0]+w1*x_i[1]+w2=0 plt.plot(svm.train_loss, linewidth=2, label='train_loss') plt.plot(svm.val_loss, linewidth=2, label='test_loss') plt.grid() plt.legend(prop={'size': 15}) plt.show() 

 d = {-1:'green', 1:'red'} plt.scatter(X_train[:,0], X_train[:,1], c=[d[y] for y in Y_train]) newline([0,-svm._w[2]/svm._w[1]],[-svm._w[2]/svm._w[0],0], 'blue') #  w0*x_i[0]+w1*x_i[1]+w2*1=0  #  x_i[0]=0, x_i[1]=0 newline([0,1/svm._w[1]-svm._w[2]/svm._w[1]],[1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=1 newline([0,-1/svm._w[1]-svm._w[2]/svm._w[1]],[-1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1 plt.show() 

 #    y_pred = svm.predict(X_test) y_pred[y_pred != Y_test] = -100 # find and mark classification error print('    : ', (y_pred == -100).astype(int).sum()) d1 = {-1:'lime', 1:'m', -100: 'black'} # black = classification error plt.scatter(X_test[:,0], X_test[:,1], c=[d1[y] for y in y_pred]) newline([0,-svm._w[2]/svm._w[1]],[-svm._w[2]/svm._w[0],0], 'blue') newline([0,1/svm._w[1]-svm._w[2]/svm._w[1]],[1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=1 newline([0,-1/svm._w[1]-svm._w[2]/svm._w[1]],[-1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1 plt.show() 

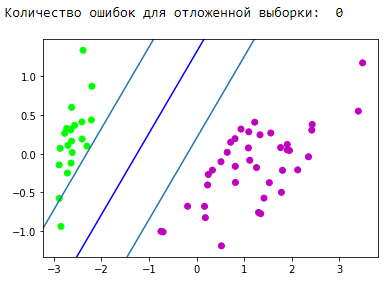
Genial Nuestro algoritmo maneja datos linealmente separables. Ahora separe las clases 0 y 1 de la clase 2:

 #    iris = load_iris() X = iris.data Y = iris.target pca = PCA(n_components=2) X = pca.fit_transform(X) Y = (Y == 2).astype(int)*2-1 # [0,1,2] --> [False,False,True] --> [0,1,1] --> [0,0,2] --> [-1,1,1] X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.4, random_state=2020) 

 #     svm = CustomSVM(etha=0.03, alpha=0.0001, epochs=300) svm.fit(X_train, Y_train, X_test, Y_test) print(svm.train_errors[:150]) # numbers of error in each epoch print(svm._w) # w0*x_i[0]+w1*x_i[1]+w2=0 plt.plot(svm.train_loss, linewidth=2, label='train_loss') plt.plot(svm.val_loss, linewidth=2, label='test_loss') plt.grid() plt.legend(prop={'size': 15}) plt.show() 

 d = {-1:'green', 1:'red'} plt.scatter(X_train[:,0], X_train[:,1], c=[d[y] for y in Y_train]) newline([0,-svm._w[2]/svm._w[1]],[-svm._w[2]/svm._w[0],0], 'blue') #  w0*x_i[0]+w1*x_i[1]+w2*1=0  #  x_i[0]=0, x_i[1]=0 newline([0,1/svm._w[1]-svm._w[2]/svm._w[1]],[1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=1 newline([0,-1/svm._w[1]-svm._w[2]/svm._w[1]],[-1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1 plt.show() 

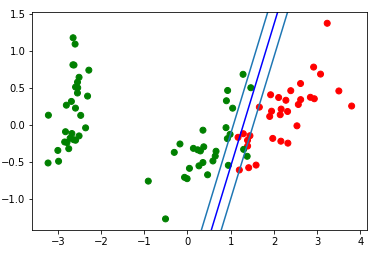
Veamos el gif, que mostrará cómo la línea divisoria cambió su posición durante el entrenamiento (solo 500 cuadros para cambiar de peso. Los primeros 300 seguidos. Las siguientes 200 piezas por cada 130 cuadros):

 import matplotlib.animation as animation from matplotlib.animation import PillowWriter def one_image(w, X, Y): axes = plt.gca() axes.set_xlim([-4,4]) axes.set_ylim([-1.5,1.5]) d1 = {-1:'green', 1:'red'} im = plt.scatter(X[:,0], X[:,1], c=[d1[y] for y in Y]) im = newline([0,-w[2]/w[1]],[-w[2]/w[0],0], 'blue') # im = newline([0,1/w[1]-w[2]/w[1]],[1/w[0]-w[2]/w[0],0], 'lime') #w0*x_i[0]+w1*x_i[1]+w2*1=1 # im = newline([0,-1/w[1]-w[2]/w[1]],[-1/w[0]-w[2]/w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1 return im fig = plt.figure() ims = [] for i in range(500): if i<=300: k = i else: k = (i-298)*130 im = one_image(svm.history_w[k], X_train, Y_train) ims.append([im]) ani = animation.ArtistAnimation(fig, ims, interval=20, blit=True, repeat_delay=500) writer = PillowWriter(fps=20) ani.save("my_demo.gif", writer='imagemagick') 

 #    y_pred = svm.predict(X_test) y_pred[y_pred != Y_test] = -100 # find and mark classification error print('    : ', (y_pred == -100).astype(int).sum()) d1 = {-1:'lime', 1:'m', -100: 'black'} # black = classification error plt.scatter(X_test[:,0], X_test[:,1], c=[d1[y] for y in y_pred]) newline([0,-svm._w[2]/svm._w[1]],[-svm._w[2]/svm._w[0],0], 'blue') newline([0,1/svm._w[1]-svm._w[2]/svm._w[1]],[1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=1 newline([0,-1/svm._w[1]-svm._w[2]/svm._w[1]],[-1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1 plt.show() 

Enderezar espacios

Es importante comprender que en problemas reales no habrá un caso simple con datos separables linealmente. Para trabajar con dichos datos, se propuso la idea de moverse a otro espacio, donde los datos serán linealmente separables. Tal espacio se llama rectificador. La rectificación de espacios y núcleos no se verá afectada en este artículo. Puede encontrar la teoría matemática más completa en la sinopsis 14,15,16 de E. Sokolov y en las conferencias de K.V. Vorontsov .

Usando SVM desde sklearn:

De hecho, casi todos los algoritmos clásicos de aprendizaje automático están escritos para usted. Pongamos un ejemplo del código, tomaremos el algoritmo de la biblioteca sklearn .

 from sklearn import svm from sklearn.metrics import recall_score C = 1.0 # = self._alpha in our algorithm model1 = svm.SVC(kernel='linear', C=C) #model1 = svm.LinearSVC(C=C, max_iter=10000) #model1 = svm.SVC(kernel='rbf', gamma=0.7, C=C) #model1 = svm.SVC(kernel='poly', degree=3, gamma='auto', C=C) model1.fit(X_train, Y_train) y_predict = model1.predict(X_test) print(recall_score(Y_test, y_predict, average=None)) 

Pros y contras de SVM clásico:

Pros:

1. funciona bien con grandes espacios de características;
2. funciona bien con datos pequeños;
3. Por lo tanto, el algoritmo encuentra maximiza la banda divisoria, que, como un airbag, puede reducir la cantidad de errores de clasificación;
4. dado que el algoritmo se reduce a resolver el problema de programación cuadrática en un dominio convexo, dicho problema siempre tiene una solución única (el hiperplano de separación con ciertos hiperparámetros del algoritmo es siempre el mismo).

Contras:

1. largo tiempo de entrenamiento (para grandes conjuntos de datos);
2. inestabilidad del ruido: los valores atípicos en los datos de entrenamiento se convierten en objetos intrusos de referencia y afectan directamente la construcción de un hiperplano de separación;
3. no se describen métodos generales para construir núcleos y rectificar espacios que sean más adecuados para un problema particular en el caso de la separabilidad lineal de clases. Seleccionar transformaciones de datos útiles es un arte.

Aplicación SVM:

La elección de uno u otro algoritmo de aprendizaje automático depende directamente de la información obtenida durante la extracción de datos. Pero en términos generales, se pueden distinguir las siguientes tareas:

• tareas con un pequeño conjunto de datos;
• tareas de clasificación de texto. SVM proporciona una buena línea de base ([preprocesamiento] + [TF-iDF] + [SVM]), la precisión del pronóstico resultante está al nivel de algunas redes neuronales convolucionales / recurrentes (recomiendo probar este método usted mismo para consolidar el material). Aquí se da un excelente ejemplo , "Parte 3. Un ejemplo de uno de los trucos que enseñamos" ;
• para muchas tareas con datos estructurados, el enlace [ingeniería de características] + [SVM] + [kernel] "todavía está lleno";
• Dado que la pérdida de la bisagra se considera bastante rápida, se puede encontrar en Vowpal Wabbit (por defecto).

Modificaciones de algoritmos:

Hay varias adiciones y modificaciones al método de vector de soporte, destinadas a eliminar ciertas desventajas:

• Máquina de vectores de relevancia (RVM)
• SVM de 1 norma (LASSO SVM)
• SVM doblemente regularizado (SVM ElasticNet)
• Máquina de características de soporte (SFM)
• Máquina de características de relevancia (RFM)

Fuentes adicionales en SVM:

1. Conferencias de texto por K.V. Vorontsov
2. Resúmenes de E. Sokolov - 14.15.16
3. Fuente genial de Alexandre Kowalczyk
4. En un habr hay 2 artículos dedicados a svm:
   
   • Año 2010
   • Año 2018
5. En el github, puedo resaltar 2 implementaciones SVM geniales en los siguientes enlaces:
   
   • MLAlgoritmos de un desarrollador nacional
   • ML-From-Scratch

Conclusión

¡Muchas gracias por su atención! Agradecería cualquier comentario, retroalimentación y consejos.
Encontrará el código completo de este artículo en mi github .

ps Gracias yorko por consejos sobre suavizar esquinas. Gracias a Aleksey Sizykh, un departamento de física y tecnología que invirtió parcialmente en código.