Buenas tardes
Como prometí en mi primer artículo , quiero familiarizarte con uno de los métodos para resolver el sistema de ecuaciones de diofantina. El propósito del artículo es familiarizar a otros lectores con esta técnica y transmitirla de una manera más o menos comprensible.
Considere un sistema de dos ecuaciones diofantinas
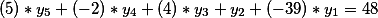
y

Encontramos todas las posibles soluciones a la primera ecuación. ¿Cómo preguntas? Seguramente hay diferentes métodos, pero compartiré en uno de los siguientes artículos cómo resolvería un problema similar. Ahora, simplemente asumimos que la solución general tiene la forma

¿Cómo comprobar que no estoy mintiendo?
Es suficiente recordar el cálculo de la matriz y multiplicar el vector de valores de nuestra primera ecuación de diofantina (sin un término libre) por la matriz de todos los coeficientes .

obtuvo el resultado del término libre y, por lo tanto, los cálculos son correctos
El siguiente paso es sustituir nuestra solución común.

en la segunda ecuación

El procedimiento es el mismo: multiplicamos el vector de los coeficientes de la segunda ecuación por la solución general de la primera
obtenemos este resultado
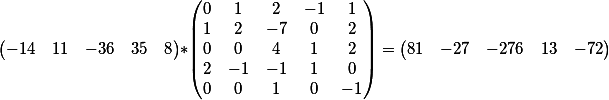
es decir, tenemos una ecuación de la forma
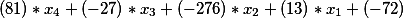
En el lado derecho de la segunda ecuación de Diophantine, como había un término libre igual a -335, se mantuvo, es decir, nuestra solución final en esta etapa tiene la forma
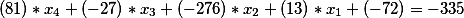
O moviendo los miembros libres a la derecha, obtenemos
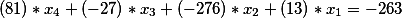
Entonces, tenemos la siguiente ecuación de diofantina. Encontremos su solución general y probémosla por la verdad.

es decir, la solución general es
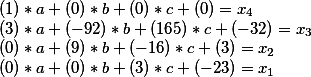
Y ahora estamos haciendo la transformación inversa (que se llame así). Es decir, el sistema

En lugar de x desconocido, sustituimos lo que sucedió en la última etapa
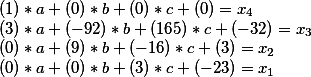
En el cálculo matricial, esto se resuelve multiplicando una matriz por otra.
Pero con la primera matriz, se debe realizar un determinado procedimiento: eliminar (temporalmente) la última columna con términos libres, ya que este parámetro no participa en la multiplicación y se utilizará más adelante.
El resultado de multiplicar dos matrices genera
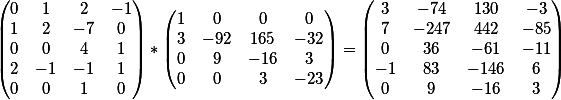
la matriz
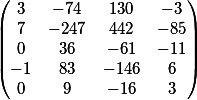
La última columna son los miembros libres de este sistema.
Tomamos en cuenta la columna que se eliminó temporalmente antes de la multiplicación y los agregamos
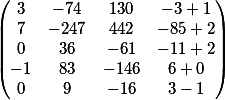
nuestra respuesta final en forma de matriz
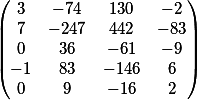
Compruébalo
El producto vectorial de los coeficientes de la primera ecuación y la matriz.
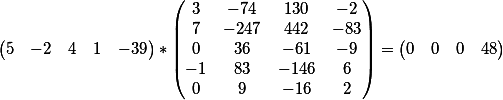
y el producto vectorial de los coeficientes de la segunda ecuación y la matriz
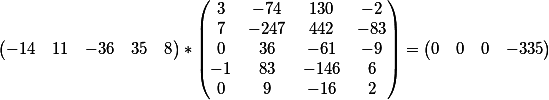
Como puede ver, el resultado coincide con el término libre de cada una de las ecuaciones.
Por lo tanto, la solución general tiene la forma
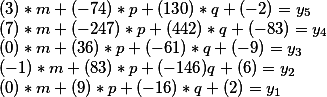
donde m, p, q - puede tomar cualquier valor entero
De una manera tan directa, es posible resolver ecuaciones lineales de diofantina más complejas. Se creó una verdadera calculadora a raíz de este algoritmo; a esta calculadora realmente no le gusta cuando ocurren ceros en lugar de los valores en los coeficientes de la primera ecuación del sistema inicial. Pero este es un problema de mi implementación específica de este algoritmo.
En el siguiente tema, te diré cómo crear ecuaciones de diofantina utilizando la matriz de la solución general. La tarea es generalmente banal y se realiza en una sola acción, pero de repente alguien no lo sabe.
Agradecería los comentarios, comentarios y sugerencias.