Durante siglos, los investigadores han buscado ejemplos de situaciones en las que las ecuaciones de Euler para la hidrodinámica de un fluido ideal resulten incorrectas. Y finalmente, los matemáticos encontraron ese ejemplo.
Durante muchos años, los matemáticos han sospechado que, bajo ciertas condiciones,
las ecuaciones de Euler se negarán a funcionar. Sin embargo, no pudieron describir el escenario específico en el que esto ocurre. Hasta hoy
Estas ecuaciones son una descripción matemática idealizada del movimiento fluido. Dentro de ciertos supuestos, modelan la propagación de olas en un estanque o la infiltración de melaza desde una lata. Deberían poder describir el movimiento de cualquier líquido en cualquier condición, y durante más de dos siglos, así fue.
Sin embargo, nueva evidencia demuestra que, bajo ciertas condiciones, estas ecuaciones aún se niegan a funcionar.
"Hace un año y medio, diría que no esperaba ver tal desarrollo incluso durante mi vida", dijo
Tarek Elgindi , matemático de la Universidad de California en San Diego, autor de un nuevo trabajo.
Elgindi demostró la existencia de fallas en las ecuaciones de Euler en dos obras publicadas en 2019, escribió
el propio
abril y
octubre , en colaboración con
Tejeddin Gole y
Nader Masmudi . El trabajo dio vuelta a un siglo de suposiciones sobre estas famosas ecuaciones para líquidos.
"Creo que este es un logro maravilloso y maravilloso", dijo
Peter Constantine , matemático de la Universidad de Princeton.
El trabajo de Elgindi no marca el final de las ecuaciones de Euler. Demuestra que, bajo ciertas condiciones, las ecuaciones parecen sobrecalentarse y comenzar a emitir tonterías. Pero en condiciones más realistas, las ecuaciones hasta ahora siguen siendo invulnerables.
Sin embargo, la excepción encontrada por Elgindi sorprendió a los matemáticos, ya que ocurre bajo condiciones bajo las cuales, como se pensaba anteriormente, la ecuación debería funcionar de todos modos.
"En general, me parece que la gente está sorprendida por el ejemplo dado por Tarek", dijo
Vlad Vikol , matemático de la Universidad de Nueva York.
Cómo se apresuraron las ecuaciones de Euler
Leonhard Euler derivó las ecuaciones para líquidos que ahora llevan su nombre en 1757. Describen la evolución de un fluido a lo largo del tiempo, tal como las ecuaciones de Newton describen el movimiento de una bola de billar sobre una mesa.
Más precisamente, estas ecuaciones denotan el movimiento instantáneo de partículas infinitesimales de un líquido. Su descripción incluye la velocidad de la partícula (qué tan rápido y en qué dirección se mueve) y una cantidad conectada con ella como la
vorticidad (qué tan rápido gira la partícula en la forma de una parte superior y en qué dirección).
Toda esta información forma completamente un "campo de velocidad", una instantánea del movimiento del fluido en un punto dado en el tiempo. Las ecuaciones de Euler comienzan con el campo de velocidad inicial y predicen cómo cambiará en cualquier momento en el futuro.
Tarek ElgindiLas ecuaciones de Euler no describen el fluido del mundo real literalmente. Estos incluyen varios supuestos no físicos. Por ejemplo, funcionan solo si los flujos internos en el fluido no crean fricción, moviéndose uno con respecto al otro. También se supone la incompatibilidad de los líquidos, es decir, de acuerdo con las reglas de las ecuaciones de Euler, es imposible comprimir un líquido, habiéndolo colocado en un espacio de un volumen menor de lo que ya ocupa.
"Este modelo puede ser imaginado como un mundo idealizado y las ecuaciones como las reglas para el movimiento de este mundo", nos escribió
Vladimir Sverak de la Universidad de Minnesota por correo electrónico.
Estas condiciones inusuales permitieron al matemático y físico John von Neumann afirmar en broma que estas ecuaciones simulan el comportamiento del "agua seca". Para simular un fluido más realista que experimente fricción interna (la llamada viscosidad), los investigadores usan
las ecuaciones de Navier-Stokes .
“Las ecuaciones de Euler están muy idealizadas. La fricción está presente en líquidos reales ”, dijo Konstantin.
Pero al mismo tiempo, las ecuaciones de Euler todavía ocupan un lugar respetado en la ciencia. Los investigadores quisieran saber si estas ecuaciones funcionan claramente en el marco de este mundo idealizado sin fricción y compresión, es decir, si pueden describir todos los estados futuros de todas las versiones iniciales posibles de los campos de velocidad. O, en otras palabras: ¿existe un movimiento tan fluido que estas ecuaciones no puedan modelar?
"En esencia, la pregunta es simple: ¿estas ecuaciones siempre hacen su trabajo?", Dijo Sverak.
En teoría, sustituyendo en las ecuaciones los valores del estado actual del líquido, obtendrá los valores exactos para describir su estado futuro. Luego puede sustituir nuevamente estos nuevos valores en las ecuaciones y extender su pronóstico. Y, por lo general, un proceso similar puede continuarse por cualquier período de tiempo en el futuro.
Sin embargo, también es posible que en condiciones muy raras se rompan las ecuaciones. Pueden crujir, soplar, producir valores de salida adecuados para el papel de futuros parámetros de entrada y, de repente, producir un valor que no es adecuado para ellos. En tales casos, los matemáticos dicen que las ecuaciones "se apresuraron".
Si las ecuaciones de Euler se apresuran, será porque comienzan a aumentar la velocidad o la vorticidad del punto de una manera poco natural. Esta ganancia será tan fuerte que en un tiempo finito la velocidad o vórtice de un punto se vuelve infinita. Y tan pronto como las ecuaciones den un valor infinito, se descompondrán y dejarán de describir las condiciones ambientales en el futuro. Esto se debe a que generalmente es imposible realizar cálculos con valores infinitos; esto es lo mismo que dividir por cero (por cierto, los valores de velocidad en este caso excederán la velocidad de la luz, aunque en el mundo idealizado del modelo no es lo peor).
Estos significados infinitos fatídicos se llaman "singularidades". Cuando los matemáticos preguntan: "¿Las ecuaciones de Euler siempre funcionan?", En realidad preguntan "¿hay escenarios en los que las ecuaciones de Euler den singularidades?"
Muchos matemáticos creen que existe, sin embargo, hasta la fecha, no pudieron encontrar un escenario específico en el que las ecuaciones realmente exploten.
"Había una sensación de que Euler estaba tratando de evitar la singularidad, y hasta hace poco, tuvo éxito", dijo Konstantin.
El nuevo trabajo no demuestra cómo las ecuaciones dan singularidades bajo condiciones en las que los matemáticos están más interesados. Sin embargo, hasta ahora este resultado se ha acercado más al objetivo que el resto. Y para esto, Elgindi consideró un modelo simplificado de movimiento fluido.
Reducción de la complejidad.
Los matemáticos tienen muchas formas diferentes de reducir la complejidad del movimiento fluido, para la simulación de las cuales usan las ecuaciones de Euler. Muchos de los resultados más interesantes, similares a los logrados por Elgindi, incluyen una demostración de cuánto puede simplificar el comportamiento del fluido, es decir, cuánto puede simplificar los datos sustituidos en las ecuaciones, y al mismo tiempo poder decir algo significativo sobre las ecuaciones en sí.
En un fluido tridimensional real, como el agua en un estanque, cualquier partícula tiene tres posibles ejes de movimiento: el eje x (izquierda-derecha), el eje y (arriba-abajo) y el eje z (adelante-atrás). Mucha libertad de movimiento. Además, el movimiento de partículas en una parte del líquido no necesariamente estará fuertemente asociado con el movimiento de partículas en otra parte.
"Tienes que hacer un seguimiento de demasiado", dijo Elgindi.
En el nuevo artículo, Elgindi simplifica el trabajo para las ecuaciones de Euler. Requiere que el líquido sea simétrico a lo largo del eje z, que generalmente no se encuentra en líquidos reales. Debido a la simetría, resulta más fácil calcular el campo de velocidad, ya que se sabe que los puntos en ambos lados del eje z son simétricos en espejo. Por lo tanto, si conoce la velocidad o vorticidad de un punto, solo necesita cambiar el signo de estos valores y obtener estos valores para otro punto.
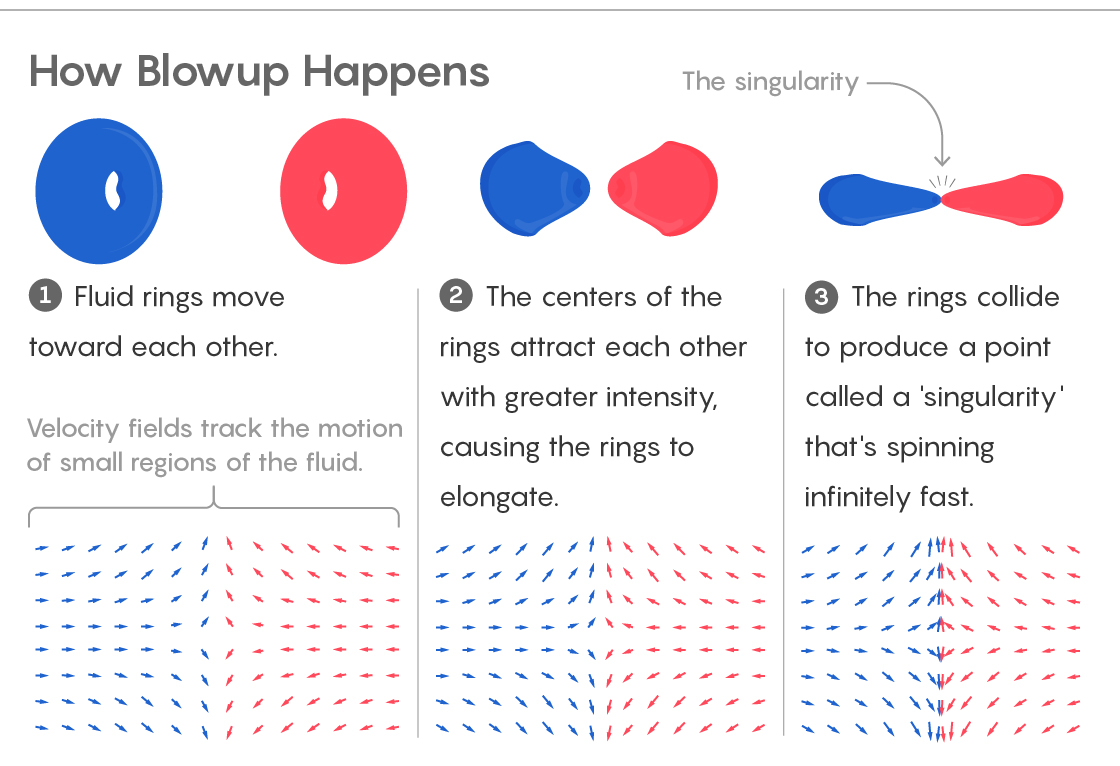1) Los fluidos se mueven hacia. Los campos de velocidad rastrean el movimiento de pequeñas secciones de fluido.
2) Los centros de los anillos son atraídos, lo que hace que los anillos se estiren.
3) Los anillos chocan, creando un punto de "singularidad", girando a velocidad infinita.También limita el posible movimiento de puntos en el fluido. Las partículas se pueden mover a lo largo del eje z, o lejos de él, o hacia él. No pueden girar alrededor del eje z. Los matemáticos dicen que no hay remolinos en tales líquidos.
"Esto reduce la tarea a dos dimensiones", dijo Elgindi.
Finalmente, Elgindi impone algunas condiciones más en los datos iniciales introducidos en las ecuaciones de Euler. En cierto sentido, estos datos son más duros que los que describen fluidos reales y aumentan la probabilidad de formación de singularidades.
En la vida real, si te mueves de un punto a otro, ubicado muy cerca de él, la velocidad de estos dos puntos será casi igual. Los vórtices de estos dos puntos también deberían ser muy similares. Los matemáticos dicen que los campos de velocidad con esta propiedad son "suaves", es decir, los valores en ellos cambian gradualmente, o suavemente, cuando se mueven de un punto a otro. No hay cambios rápidos.
Pero en el caso de la descripción del líquido de Elgindi, todo es diferente.
"El giro en los datos de Tarek puede cambiar mucho", dijo Vikol. "Los puntos cercanos pueden tener vórtices muy diferentes".
Puede parecer que las simplificaciones de Elgindi se apartan mucho del comportamiento de los líquidos reales para ser útiles. Sin embargo, todavía son mucho menos rígidos que muchos de los escenarios simplificados en los que los científicos consideraron previamente las ecuaciones de Euler. De hecho, Elgindi incluso demostró que bajo estas condiciones simplificadas, pero no demasiado, las ecuaciones de Euler comienzan a producir resultados muy inesperados.
Juego terminado
Para comprender el descubrimiento de Elgindi, imagine un recipiente con agua. Este no es un ejemplo exacto, ya que el trabajo de Elgindi considera líquidos que no tienen límites, es decir, volar como una burbuja en gravedad cero. Pero para visualizar el guión, que está en el centro de su trabajo, será útil disponer el agua en el tanque. Aunque las hipótesis matemáticas más importantes, y las más difíciles de probar, se refieren a líquidos sin límites.
Luego imagine dos gruesos anillos de agua ubicados en diferentes extremos del tanque. Forman pequeños embudos, como remolinos, disturbios organizados dentro del fluido. Fenómenos similares se encuentran en la naturaleza, y son similares a los anillos de humo que los fumadores experimentados pueden dar.
Ahora imagine cómo se unen dos anillos opuestos.
Durante el enfoque, las ecuaciones de Euler funcionan normalmente, contando los campos de velocidad que describen el fluido en cada momento en el tiempo. Pero cuando se acercan lo suficiente, las ecuaciones comienzan a producir resultados muy extraños.
Muestran cómo los anillos comienzan a atraerse entre sí cada vez más, y los puntos centrales de los anillos se atraen entre sí incluso más que las partes externas. Como resultado, los anillos se extienden y comienzan a parecerse a un embudo. Y cuanto más se acercan los centros de los anillos, más aumenta su velocidad. Y luego chocan.
Y si en este momento observa el campo de velocidad que describe la colisión, puede ver que con este conjunto de supuestos en toda la historia de las ecuaciones de Euler nadie vio: la singularidad. Elgindi demostró que las ecuaciones de Euler dan una velocidad infinita en el punto de colisión. El juego ha terminado.
"La forma clásica de la ecuación se rompe", dijo Elgindi. "Después de eso, no está claro qué está pasando".
El resultado tiene sus limitaciones. Es decir, es imposible extrapolar el comportamiento de las ecuaciones de Euler en condiciones completamente "suaves" basadas en este resultado. Hace unas décadas, los matemáticos demostraron que, en condiciones "suaves", el escenario considerado por Elgindi no producirá una singularidad.
Sin embargo, el resto de su resultado cambia por completo la opinión de los matemáticos sobre estas viejas ecuaciones.
Antes del trabajo de Elgindi, los matemáticos no podían probar la existencia de una situación en un fluido sin límites, en el que las ecuaciones de Euler funcionan durante algún tiempo (mientras los anillos se unen), pero no infinitamente. En todos los trabajos anteriores, los matemáticos demostraron que si las ecuaciones básicamente funcionan, siempre funcionan.
"Este es un resultado muy notable, ya que demuestra la presencia de singularidades en el escenario, que llamamos 'correctamente definido'". Tiene sentido, pero al mismo tiempo llegamos a una singularidad en un tiempo finito ”, dijo Konstantin.
Muchas generaciones de científicos han estado buscando un punto débil en las ecuaciones de Euler. Y finalmente, con algunas reservas, el matemático lo encontró.