Sobre el significado geométrico de los códigos grises

Los códigos grises tienen un parentesco cercano con la curva de Hilbert .

Sin embargo, al comunicarse con sus colegas, resultó que esta simple adicción se ve en sus ojos como algo no trivial. Una búsqueda en Internet no dio más que una frase turbia en la wiki: "Las curvas de Hilbert en espacios de mayor dimensión son representantes de generalizaciones de códigos grises". Por lo tanto, había un deseo de abrir el tema, brevemente, en un lenguaje simple.

Como resultado, bajo el corte - "escándalos, intrigas, investigaciones".

La característica principal del código Gray es que dos valores lexicográficamente adyacentes difieren solo en una categoría. Por otro lado, la curva de Hilbert es continua: la distancia entre dos puntos adyacentes es siempre uno. Esto solo insinúa su conexión interna.

El código Gray describe las ocurrencias de una curva de Hilbert dentro de un solo hipercubo. De hecho, si tomamos un código de 3 bits y lo dibujamos en un espacio tridimensional (tomando cada bit para la coordenada correspondiente), obtenemos


Figura 1 Código gris de 3 bits como un cubo tridimensional

¡La imagen familiar es el simplex tridimensional de la curva de Hilbert! Reemplazando sucesivamente cada nodo del símplex con el mismo símplex (teniendo en cuenta las rotaciones y los reflejos para mantener la continuidad), obtenemos una curva de Hilbert 4x4x4.

Continuando con estas iteraciones, podemos llenar continuamente una red cúbica de cualquier tamaño.


Figura 2 varias iteraciones del simplex de la curva de Hilbert.

¿Pero cómo sucedió?

Se sabe que el código Gray es auto similar. A veces se le llama espejo “debido al hecho de que la primera mitad de los valores al cambiar el orden es equivalente a la segunda mitad, con la excepción del bit alto. El bit más significativo es simplemente invertido ". Para mayor claridad, el código de 3 bits es el bit más significativo, el más a la izquierda:



Como estamos hablando de la autosimilitud, comencemos desde el principio, con un código de un bit. Hablando estrictamente, sería posible comenzar con una dimensión cero: puntos, esto fundamentalmente no cambia nada, solo las palabras tendrían que escribirse más.

El código de un solo dígito de Gray es aún más simple que un rifle de tres líneas, es 0 o 1.

Geométricamente, esto corresponde a un cubo de unidad unidimensional: un segmento. Puede moverse a lo largo de un segmento, ya sea de principio a fin, o de principio a fin, hasta la simetría, esto es lo mismo. Sin embargo, llamaremos al principio el lugar donde el valor es menor (recuerde que los lados del cubo son dígitos del número) y el final, donde es más.

Pasamos al caso bidimensional. Un cubo bidimensional es un cuadrado. Teniendo en cuenta la autosimilitud, clonamos el cubo unidimensional (0,1) y obtenemos dos segmentos: (0,0 -> 1,0) y (0,1 -> 1,1). Ahora necesita conectar estos segmentos para moverse alrededor del cuadrado. Y aquí surgen dos opciones:

• conectamos el comienzo de la iteración anterior: el cubo unidimensional con el comienzo de su clon. Hasta la simetría, esto es lo mismo que conectar el extremo al final. El tipo de simetría es espejo. Esta opción se llama condicionalmente "misionera".
  
• conectamos el final de la iteración anterior con el comienzo de su clon. Hasta la simetría, esto es lo mismo que unir el comienzo de una línea con el final de un clon. El tipo de simetría es central. Llamamos a esta opción un "tren".

Actuamos de manera similar al pasar a tres o más casos dimensionales.


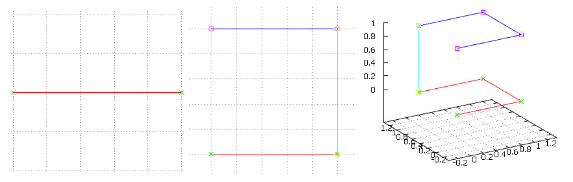Figura 3 Las dos primeras iteraciones de la versión "misionera"

Aquí la iteración anterior está resaltada en rojo, su clon está en azul y su conexión está en turquesa.

Tenga en cuenta que la conexión siempre pasa por una única dimensión: la recién agregada, por lo tanto, la característica principal del código Gray aparece debido a la auto-similitud. Y dado que el final de la iteración anterior está conectado con el final de su clon, se produce un "reflejo": al dar la vuelta, nos vemos obligados a atravesar el clon en el orden inverso. Independientemente de la dimensión. Aquí puede ver el origen y las características de la curva de Hilbert; no importa cuán grande sea la red (de cualquier dimensión), a nivel de base sigue siendo el mismo cubo unitario con transiciones de longitud uno.


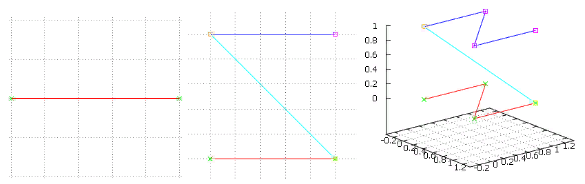Figura 4 Las dos primeras iteraciones de la opción "entrenar", los mismos colores

Pero esta música también nos es familiar: tenemos una curva Z simplex. La palabra simplex aquí también significa que si tomamos cada uno de sus puntos y lo reemplazamos con un simplex, obtenemos un cubo de 4x4x4, iteraciones continuas: podemos llenar una red cúbica arbitrariamente grande.

Es curioso que en este caso, la conversión de la ruta pasada desde el origen al código, que se puede analizar en bits, sea trivial.
Mientras que el caso del código Gray es G = W ^ (W >> 1), donde W es la longitud aprobada, G es el código Gray.


Figura 5 primeras dos iteraciones de la curva Z (wiki)


6 para comparar, las dos primeras iteraciones de la curva de Hilbert (wiki)

Pero no hay otras opciones (naturales) para eludir un solo hipercubo.
Entonces resulta que donde sea que lances, alrededor de Hilbert, Lebesgue ... y el vacío .

PD : en la imagen del título, un codificador circular con un código Gray de ocho dígitos.
PPS : aquí me corrigen que el simplex es un término bien establecido, no es bueno con él. Bueno, este artículo no es solo un simplex, sino un simplex de una curva de Hilbert o un simplex de una curva Z. Que los matemáticos fieles me perdonen.