Modelo automatizado de gestión de programas

1. Introducción

En [1], se respondió a la pregunta de lo que se considera programación automática (AP), pero el modelo de una máquina de estados finitos (SC) no se describió en detalle como un modelo de control de programas automáticos. Está claro que un autómata abstracto puro no es adecuado para este papel, porque limitado por el número de canales. Pero el modelo estructural del autómata, así como la teoría de los autómatas estructurales que le corresponden, todavía no permiten dar una respuesta sobre la elección del modelo de autómata.

El problema comienza con el hecho de que entre los muchos trabajos sobre la teoría de autómatas finitos (TCA) hay pocos que den una definición del modelo de un autómata estructural finito (SCA). Es cierto que uno puede entender que un autómata estructural es un diagrama [estructural] de autómatas elementales (elementos funcionales) que implementa un modelo de autómata abstracto [2]. Recuerde que, de acuerdo con la teoría, todo comienza con la creación de un modelo de dispositivo en forma de autómata abstracto, y luego la tarea es sintetizar un circuito digital que lo implemente [3].

La programación a primera vista se parece un poco a una síntesis de circuitos digitales. Pero solo al principio. En primer lugar, todo comienza con un algoritmo. En segundo lugar, los problemas estructurales de organizar e implementar circuitos digitales y programación tienen mucho en común, especialmente en el contexto de la programación paralela. Pero discutiremos el tema del paralelismo por separado. Mientras tanto, nuestra tarea es elegir y / o modificar el modelo de una máquina de estados finitos, lo que sería comprensible, conveniente y agradable para los programadores mimados por diversas herramientas de software.

Es cierto que la pregunta es inmediatamente lógica: ¿por qué un "kit de herramientas automático" más y bastante inusual? Intentaremos responder a esta pregunta definiendo un modelo de control automático [anidado], considerando también sus ventajas en comparación con el modelo de programación habitual.

2. Definición del modelo de control de programas automáticos.

En el proceso de evolución, la práctica de la programación ha formado ciertos requisitos para el modelo de gestión del programa. Debe reconocerse que el modelo de una máquina clásica de estados finitos les corresponde bastante poco. Y si la tarea es utilizar autómatas en la programación, entonces debe adaptarse. Esto es deseable hacerlo en el marco de la teoría de los autómatas. Las principales reclamaciones al AP existente se reducen al hecho de que esta condición se viola.

Definición 1. Llamamos a la forma normal disyuntiva de autómatas finitos (DNFA) autómatas finitos completamente definidos cuyas transiciones están etiquetadas por conjunciones elementales de variables lógicas.

El modelo de ADN se basa en modelos formales de autómatas totalmente (totalmente) definidos con un estado abstracto [4] y autómatas lógicos [5].

Definición 2. Llamamos a la forma disyuntiva de un autómata finito (DFA) un autómata en forma de un DFA que contiene solo las transiciones resultantes .

Las transiciones marcadas con señales de salida y las transiciones con un guión en lugar de las señales de salida que cambian el estado actual del autómata se clasifican como transiciones efectivas. Las transiciones que no están incluidas en la descripción del autómata disyuntivo constituyen una adición del DKA (DDA) al autómata DFA completamente definido. Tal adición es un autómata que consiste en estados aislados con transiciones en forma de bucles y con guiones en lugar de las señales de salida.

3. El modelo de memoria para el modelo de cálculo AP

La presencia de muchas entradas y salidas del DFA establece el paralelismo de los operadores / funciones de software asociados con él. Para su correcta implementación, se requiere un modelo de memoria del tipo CREW (lectura simultánea exclusiva - escritura) [6]. Dentro de su marco, la lectura de valores de datos actuales está permitida por parte del conjunto de todas las funciones (predicados y acciones), y solo una de ellas puede cambiar datos generales para acciones ejecutables paralelas.

El modelo de control automático, en contraste con el modelo informático de subprocesos múltiples, limita claramente la ejecución de los operadores / funciones del programa automático a los límites de un ciclo de tiempo discreto. En tal situación, cualquier cambio en la memoria por acciones realizadas en el ciclo de reloj actual puede escribirse en la "memoria oculta" , de modo que después de que se completen y antes del inicio del siguiente ciclo de reloj discreto, se conviertan en sus nuevos valores.

La interacción de los operadores de programas de autómatas con la memoria se denominará modelo de memoria oculta . Este modelo es una parte esencial del modelo general de programación automática. Asegura la corrección del funcionamiento paralelo de los operadores AP y simplifica la programación de procesos paralelos.

Dentro del marco del modelo de memoria, en realidad no se necesitan mecanismos complejos y poco confiables para la sincronización multiproceso de los procesos (para más detalles ver [7]). Pero si es necesario, debido a la equivalencia de autómatas y esquemas gráficos de algoritmos (GAW) [8], el modelo de programación automática no limita su aplicación.

4. Modelos anidados e inerciales de autómatas

La tarea de crear un modelo del elemento lógico del retraso, elegido además como ejemplo, por un lado, demuestra los problemas del modelo clásico del autómata y, por otro lado, refleja las cualidades del modelo DKA que resuelve problemas algorítmicos con medios más visuales y convenientes. El modelo introducido de autómatas anidados genera una subclase de modelos de autómatas, en lo sucesivo denominados autómatas inerciales , y una subclase correspondiente de algoritmos inerciales .

Entonces, que sea la tarea de crear un modelo discreto de un elemento lógico de retardo que implemente la transmisión de una señal de entrada binaria. Además, los tiempos de sus retrasos t01 y t10, respectivamente, a los estados unitarios y cero en el caso general no coinciden.

El modelo más simple de un solo retraso en forma de autómata Mealy se muestra en la Fig. 1 (ver, para comparación, el modelo de retraso en [2]). Sus retrasos están determinados por un único ciclo de reloj discreto. Se presentan modelos más complejos de retrasos en el transporte (para más detalles sobre los tipos de retrasos, véase [9]) en forma de un autómata Miley y un modelo combinado de Miley-Moore, respectivamente, en la Fig. 2a y la fig. 2b.


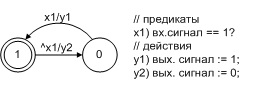
Fig. 1. Modelo de unidad de retraso en forma de autómata Miles


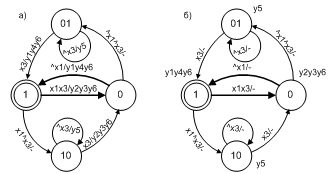
Fig. 2. El modelo de retraso de transporte de Miles (a) y Miles-Moore (b)

La señal de entrada x3 (recordamos que en el programa automático corresponde al predicado [1]) toma un valor verdadero si el valor del contador de reloj es igual al valor de la variable t igual al retraso t01 o t10. El valor de la variable t se asigna a las señales y3 e y4 (en el programa, las funciones de acción del mismo nombre que las señales de salida). Las señales y1, y2 establecen el valor de la variable que representa la salida del modelo. La señal y5 incrementa el contador del reloj, que se restablece mediante la señal y6.

Observación 2. Los estados internos del modelo en la Fig. 1, es conveniente asociarlo con un estado de salida de un elemento. Esto nos permite excluir no solo los operadores y1 e y2, sino también la propia variable de salida.

La implementación de la incorporación de autómatas similar a las subrutinas de llamadas forma la tecnología de la programación de autómatas modulares. Al mismo tiempo, a nivel de software, en contraste con intentos similares a nivel de hardware (ver [10] para comparación), esto es mucho más simple. Para hacer esto, debe insertar la llamada al programa del autómata anidado, y luego el núcleo de la implementación de autómatas, como un procesador normal, organiza el retorno del control al nivel actual de anidamiento.

Definición 3. Los autómatas anidados se denominarán autómatas con un estado final, cuya transición inicia el procedimiento de volver al nivel (rango) anterior de anidamiento.

La implementación correcta de la anidación de autómatas impone restricciones en el procedimiento para su creación. En primer lugar, un autómata anidado solo puede estar subordinado. Además, un autómata de nivel superior, excluido el rango cero, también puede ser un autómata anidado. En segundo lugar, en cualquier transición solo se puede crear un autómata anidado. El mecanismo de los autómatas anidados también crea la base para la implementación de algoritmos recursivos basados ​​en el control automático.


Fig. 3. Modelo de retraso en forma de autómatas anidados

La Fig. 3 muestra el modelo de retraso, donde la Fig. 3a representa el modelo de nivel superior, y las Fig. 3b y Fig. 3c: variantes de autómatas anidados para el transporte y los retrasos de inercia (para más detalles sobre los tipos de retrasos, consulte [8]). Al mismo tiempo, estos son ejemplos de dos tipos de autómatas anidados: ordinarios e inerciales . El tipo de un autómata anidado se define por el nombre de sus estados finales: un estado con el nombre "00" determina la salida habitual del autómata anidado, y un estado con el nombre "XX" no cambia el estado actual del autómata de nivel superior.

Una explicación importante para comprender el algoritmo de retraso de inercia. Para ello (ver Fig. 3c), el valor del predicado x1 depende de la transición en la que se crea el autómata incorporado. En otras palabras, el predicado en el estado "0" controla la preservación de "cero" en la entrada, y en el estado "1", por el contrario, "unidades". Si el valor en la entrada es cero en el valor cero de la salida, entonces necesita devolver el valor verdadero. Además, si se viola la estabilidad de la entrada (el valor x1 es falso) y el tiempo de retraso no ha expirado (el valor x3 es falso), la salida de la máquina integrada se realiza a través del estado de inercia (ver Fig. 3c).

Definición 4. Los autómatas, incluida la llamada de autómatas anidados que tienen un estado de inercia final, se denominarán autómatas inerciales .

En el modelo de la Fig. 3a, la acción z1 (el símbolo z se selecciona para los nombres de acciones que incluyen una llamada a un autómata anidado) crea un autómata anidado si se define un valor de retraso. Como parte de esta acción, se determina el tipo de retraso especificado, de acuerdo con el cual se crea uno de los autómatas anidados, que se muestra en la Fig. 3b o la Fig. 3c.

En el nivel superior de la jerarquía, la vista del autómata en la Fig. 3a coincide completamente en estructura con el modelo en la Fig. 1, y solo difiere en presencia de acciones en las transiciones. Los retrasos con autómatas anidados tienen una forma más simple en comparación con el modelo de un solo nivel en la figura 2. Un autómata anidado también puede considerarse como una especie de "autómata de biblioteca" al que se puede llamar desde cualquier otro autómata.

3. Programación de autómatas de objetos.

El modelo de control automático, además de la forma gráfica, también tiene una forma tabular simple: una tabla de transición (TP), que se puede interpretar eficazmente en C ++. Dentro de su marco, un programa de autómata separado (o una parte de él) y, en consecuencia, su definición en forma de un circuito de programa S puede ser representado por una clase. En este caso, los modelos de memoria corresponderán a las propiedades de la clase, el conjunto de operaciones corresponderá a los métodos de la clase y el control automático en forma de TP describirá el comportamiento de la clase. La introducción del control en la clase nos permite hablar sobre objetos activos, también llamados a menudo agentes, etc.

Muchos objetos con comportamiento en forma de control de autómatas formalizan el concepto de un programa paralelo de autómatas de objetos . En este caso, el modelo de cualquier programa paralelo puede representarse mediante un diagrama de programa en el que el control C se presentará en forma de una red de autómatas, donde los autómatas componentes describen el comportamiento de los objetos activos, la memoria M está representada por una combinación de propiedades de objetos, y muchos operadores A están representados por una combinación de métodos de objetos de programa.

En el entorno VKPA, la función del lenguaje de programación automatizado se asigna al lenguaje C ++. En “C ++ automático”, los objetos están dotados de actividad / comportamiento y tienen los medios para describir e implementar paralelismo, tanto a nivel de métodos de objetos individuales como a nivel de describir la operación paralela de muchos objetos.

Las implementaciones de objetos existentes de AP son bastante complicadas. En VKPa, su implementación de objetos se basa en la interpretación de autómatas y el control dedicado del programa. A diferencia de la implementación directa de autómatas, utilizada, por ejemplo, en la tecnología SWITH, esto elimina el procedimiento para convertir un modelo de autómata en un modelo de diagrama de flujo. El algoritmo de interpretación utilizado en VKPa es similar al método de interpretación de tablas de decisión de E. Hamby [12].

A menos que se especifique lo contrario, asociaremos aún más el concepto de un programa de autómatas con el concepto de un objeto de autómatas (AO) en el sentido de OOP, pero teniendo en cuenta el concepto de un programa paralelo de autómatas de objetos presentado anteriormente. Debido a esto, los operadores y la memoria del AP se determinarán a través de los métodos y propiedades de los objetos activos. Los objetos de autómatas se distinguen de los objetos ordinarios por la presencia de comportamiento determinado por el modelo de máquina de estados.

4. Conclusiones

Crear un modelo de autómatas anidados es un paso hacia un cambio cualitativo en la tecnología de programación. El modelo de inercia descrito del autómata es similar al concepto de estados históricos en UML. La incrustación habitual de autómatas tiene una programación analógica, la "incrustación inercial" no la tiene, porque En un programa, no puede volver a un comando que precede a una llamada de subrutina. Y estos son elementos de una diferencia cualitativa entre la programación automática y la programación ordinaria.

Por supuesto, puede introducir la memoria en la sombra en la programación ordinaria y denotar el paralelismo de las funciones. Pero en el marco del modelo de autómata, todo esto tiene una forma orgánica, tanto en términos de descripción como en términos de rendimiento. Todo está determinado por el paralelismo natural del modelo. El modelo de diagrama de bloques no tiene tales capacidades.

Los objetos activos también amplían las capacidades de programación. Pero el "contenedor de objetos", por su parte, afecta cualitativamente la programación automática, simplificando los procedimientos para invocar e implementar autómatas anidados. Por lo tanto, el uso de las propiedades de clase [local] le permite implementar no solo la incrustación, sino también cualquier algoritmo recursivo.