Teoría de la información visual (parte 2)

La segunda parte de la traducción de Longrid se dedica a la visualización de conceptos desde la teoría de la información. La segunda parte trata de entropía, entropía cruzada, divergencia Kullback-Leibler, información mutua y bits fraccionales. Todos los conceptos cuentan con excelentes explicaciones visuales.

Para completar la percepción, antes de leer la segunda parte, le recomiendo que se familiarice con la primera .

Cálculo de entropía

Recordemos que el costo de un mensaje es largo $$$L$ es igual a $$$\ frac {1} {2 ^ L}$ . podemos invertir este valor para obtener la longitud del mensaje que vale la cantidad dada: $$$\ log_2 (\ frac {1} {cost})$ . Ya que pasamos $$$p (x)$ por palabra de código para $$$x$ , la longitud será igual $$$\ log_2 (\ frac {1} {p (x)})$ . En la figura, la elección de las mejores longitudes de palabras de código.



Discutimos anteriormente que hay un límite fundamental para cuán corto puede ser un mensaje promedio para transmitir eventos desde una distribución de probabilidad dada $$$p$ . Este límite, la longitud promedio del mensaje cuando se utiliza el mejor sistema de codificación, se denomina entropía $$$p, H (p)$ . Ahora que conocemos la longitud óptima de la palabra de código, ¡podemos calcularla!

$$

$$H (p) = \ sum_xp (x) \ log_2 \ Bigg (\ frac {1} {p (x)} \ Bigg)$$

(A menudo, la entropía se escribe como $$$H (p) = - \ sum p (x) \ log_2 (p (x))$ usando la igualdad $$$\ log (1 / a) = - \ log (a)$ . Me parece que la primera versión es más intuitiva, por lo que continuaremos usándola).

Si quiero informar qué evento sucedió, no importa lo que haga, en promedio necesito enviar tantos bits.

La cantidad promedio de información necesaria para transmitir algo tiene consecuencias directas para la compresión. ¿Pero hay otras razones por las que debemos ocuparnos de esto? Si! Describe mi incertidumbre y hace posible cuantificar la información.

Si supiera con certeza lo que sucedería, ¡no tendría que enviar un mensaje en absoluto! Si hay dos cosas que pueden suceder con una probabilidad del 50%, solo necesito enviar 1 bit. Pero si hay 64 eventos diferentes que pueden ocurrir con la misma probabilidad, tendré que enviar 6 bits. Cuanto más concentrada es la probabilidad, más oportunidades tengo para crear código inteligente con mensajes cortos y medios. Cuanto más vaga sea la probabilidad, más largas deberían ser mis publicaciones.

Cuanto más incierto es el resultado, más aprendo en promedio cuando me cuentan lo que sucedió.

Entropía cruzada

Poco antes de mudarse a Australia, Bob se casó con Alice, también imaginaria. Para mi sorpresa, así como para la sorpresa de otros personajes en mi cabeza, Alice no era una amante de los perros. Ella era una amante de los gatos. A pesar de esto, pudieron encontrar un lenguaje común en su obsesión general con los animales y su vocabulario muy limitado.



Estos dos usan las mismas palabras, solo que con diferentes frecuencias. Bob habla de perros todo el tiempo, Alice habla de gatos todo el tiempo.

Alice primero me envió mensajes usando el código de Bob. Desafortunadamente, sus publicaciones fueron más largas de lo requerido. El código de Bob ha sido optimizado para su distribución de probabilidad. Alice tiene una distribución de probabilidad diferente, y el código no es óptimo para ella. La longitud promedio de la palabra de código cuando Bob usa su código es 1.75 bits; cuando Alice la usa, entonces 2.25. ¡Sería aún peor si los dos no fueran tan similares!

La longitud promedio del mensaje de una distribución con el código óptimo para otra distribución se denomina entropía cruzada. Formalmente, podemos definir la entropía cruzada de la siguiente manera:

$$

$$H_p (q) = \ sum_xq (x) \ log_2 \ Bigg (\ frac {1} {p (x)} \ Bigg)$$

En este caso, estamos hablando de la entropía cruzada de la frecuencia de las palabras de la catworm de Alice con respecto a la frecuencia de las palabras de Bob, el cuidador de perros.



Para reducir el costo de nuestra conexión, le pedí a Alice que usara su propio código. Para mi alivio, esto redujo la longitud promedio del mensaje. Pero esto creó un nuevo problema: a veces Bob usaba accidentalmente el código de Alice. Sorprendentemente, ¡es peor cuando Bob usa el código de Alice que cuando Alice usa el código de Bob!

Entonces ahora tenemos cuatro posibilidades:

• Bob usa código nativo ( $$$H (p) = 1.75$ poco)
• Alice usa el código de Bob ( $$$H_p (q) = 2.25$ poco)
• Alice usa su propio código ( $$$H (q) = 1.75$ poco)
• Bob usa el código de Alice ( $$$H_q (p) = 2.375$ poco)

Esto no es tan intuitivo como uno podría pensar. Por ejemplo, podemos ver que $$$H_p (q) ≠ H_q (p)$ . ¿Podemos de alguna manera ver cómo estos cuatro significados se relacionan entre sí?

En el siguiente diagrama, cada subgrafo representa una de estas 4 posibilidades. Las ilustraciones visualizan la longitud promedio de un mensaje. Están organizados en un cuadrado, por lo que si los mensajes son de la misma distribución, los gráficos están cerca, y si usan los mismos códigos, están uno encima del otro. Esto le permite combinar visualmente distribuciones y códigos juntos.



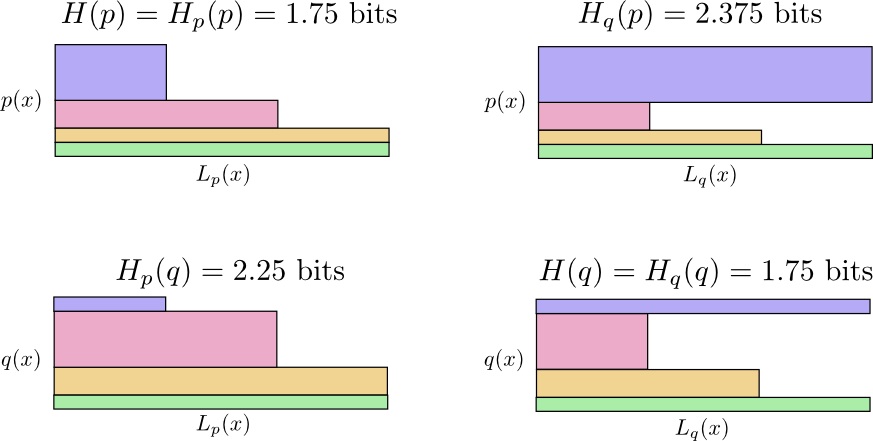
Mira por qué $$$H_p (q) ≠ H_q (p)$ ? $$$H_q (p)$ tan grande, porque el evento marcado en azul a menudo ocurre cuando $$$p$ pero obtiene una palabra de código larga porque es muy rara para $$$q$ . Por otro lado, eventos frecuentes con $$$q$ menos común con $$$p$ pero la diferencia es menos dramática, por lo tanto $$$H_p (q) Hp (q)$ un poco menos

La entropía cruzada no es simétrica.

Entonces, ¿por qué debería importarle la entropía cruzada? La entropía cruzada nos da una manera de expresar cuán diferentes son las dos distribuciones de probabilidad. Cuanto más diferentes son las distribuciones $$$p$ y $$$q$ la mayor entropía cruzada $$$p$ con respecto $$$q$ habrá más entropía $$$p$ .



Del mismo modo cuanto más $$$q$ diferente de $$$p$ la mayor entropía cruzada $$$q$ con respecto $$$p$ habrá más entropía $$$q$ .

Lo realmente interesante es la diferencia entre entropía y entropía cruzada. Esta diferencia es igual a la duración de nuestras publicaciones, porque utilizamos código optimizado para otra distribución. Si las distribuciones son las mismas, entonces esta diferencia será cero. A medida que aumentan las diferencias, se hará más grande.

Llamamos a esta diferencia divergencia Kullback-Leibler, o simplemente divergencia KL. KL divergencia $$$p$ con respecto $$$q$ , $$$D_q (p)$ definido de la siguiente manera:

$$

$$D_q (p) = H_q (p) - H (p)$$

Lo mejor de la divergencia KL es que parece la distancia entre dos distribuciones. ¡Mide lo diferentes que son! (Si tomas esta idea en serio, llegarás a la geometría de la información).

La entropía cruzada y la divergencia KL son increíblemente útiles en el aprendizaje automático. A menudo queremos que una distribución esté cerca de otra. Por ejemplo, podemos querer que la distribución predicha se acerque a la verdad subyacente. La divergencia KL nos da una forma natural de hacer esto, y por lo tanto se manifiesta en todas partes.

Entropía y varias variables.

Volvamos a nuestro ejemplo de clima y ropa dado anteriormente:




A mi madre, como a muchos padres, a veces le preocupa que no me vista adecuadamente para el clima. (Ella tiene buenas razones para sospechar: a veces no uso un impermeable en invierno). Por lo tanto, a menudo quiere saber el clima y lo que llevo puesto. ¿Cuántos bits debo enviarle para informar esto?

La forma más fácil de pensar en esto es igualar la distribución de probabilidad:



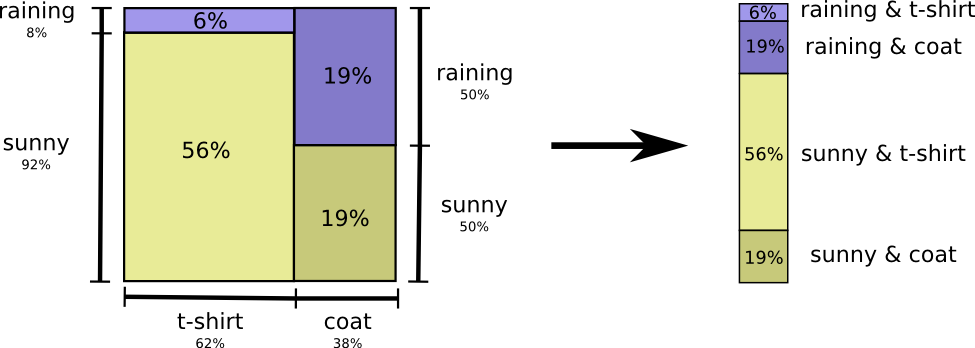
Ahora podemos calcular las palabras de código óptimas para eventos con tales probabilidades y calcular la longitud promedio del mensaje:



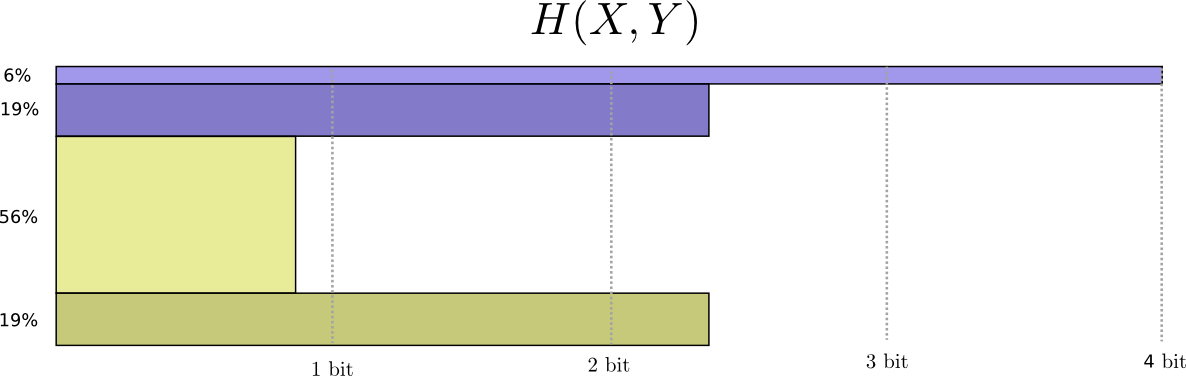
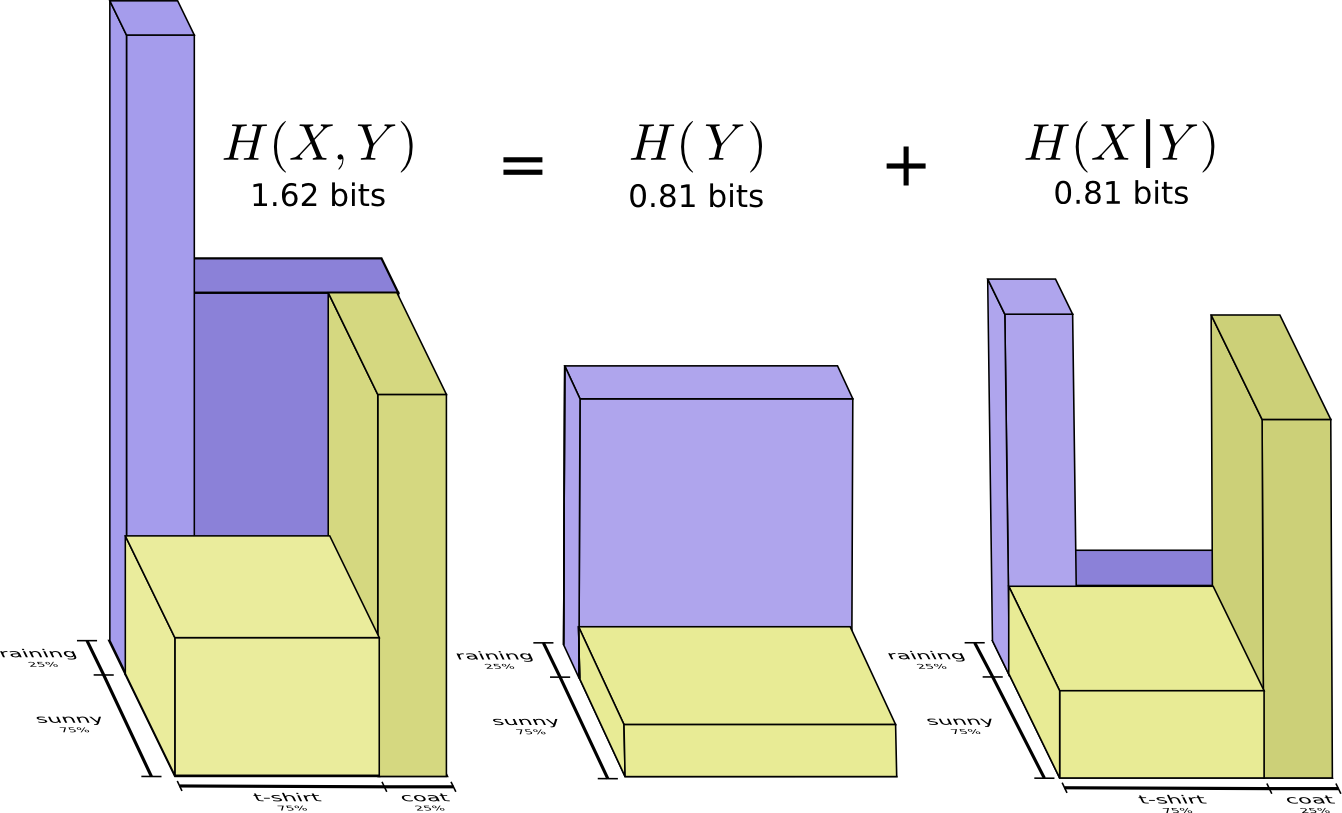
Lo llamamos entropía conjunta $$$X$ y $$$Y$ definido de la siguiente manera:

$$

$$H (X, Y) = \ sum_ {x, y} p (x, y) \ log_2 \ bigg (\ frac {1} {p (x, y)} \ bigg)$$

Coincide con nuestra definición habitual, con la excepción de dos variables en lugar de una.

Se obtiene una imagen ligeramente mejor de esto, sin igualar la distribución, representando la longitud de la palabra de código en la tercera dimensión. ¡Ahora la entropía es volumen!



Pero supongamos que mi madre ya sabe el clima. Ella puede verla en las noticias. ¿Cuánta información necesito proporcionar?

Parece que necesito enviar suficiente información para decirme qué ropa estoy usando. Pero, de hecho, necesito enviar menos información, porque ¡qué clima usaré depende mucho del clima! Veamos el caso de la lluvia y el sol por separado.



En ambos casos, no necesito enviar demasiada información en promedio, porque el clima me da una buena idea de cuál será la respuesta correcta. Cuando el sol, puedo usar un código especial optimizado para el sol, y cuando llueve, puedo usar el código optimizado para la lluvia. En ambos casos, envío menos información que si usara un código común para ambos. Para obtener la cantidad promedio de información que necesito enviar a mi madre, solo reúno estos dos casos ...



Llamamos a esto entropía condicional. Si lo formaliza en una ecuación, obtiene:

$$

$$H (X | Y) = \ sum_yp (y) \ sum_xp (x | y) \ log_2 \ bigg (\ frac {1} {p (x | y)} \ bigg)$$

$$

$$= \ sum_ {x, y} p (x, y) \ log_2 \ bigg (\ frac {1} {p (x | y)} \ bigg)$$

Información mutua

En la sección anterior, descubrimos que conocer una variable puede significar que se necesita menos información para comunicar el valor de otra variable.

Una buena manera de pensarlo es imaginar la cantidad de información en forma de rayas. Estas bandas se superponen si hay información común entre ellas. Por ejemplo, parte de la información en $$$X$ y $$$Y$ común por lo tanto $$$H (X)$ y $$$H (Y)$ son rayas superpuestas. Y desde $$$H (X, Y)$ Es la información de ambas variables, entonces esta es la unión de las bandas $$$H (X)$ y $$$H (Y)$ .



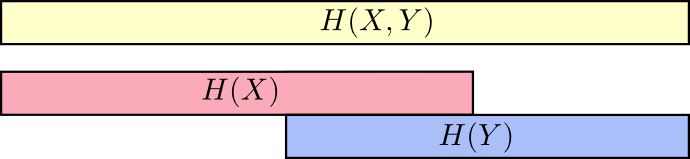
Cuando pensamos en las cosas de esta manera, mucho se vuelve más fácil de ver.

Por ejemplo, ya hemos notado que para transmitir información como $$$X$ así y $$$Y$ ("Entropía conjunta", $$$H (X, Y)$ ) se requiere más información que solo para la transmisión $$$X$ ("Entropía definitiva", $$$H (X)$ ) Pero si ya lo sabes $$$Y$ luego para la transmisión $$$X$ ("Entropía condicional", $$$H (X | Y)$ ) se requiere menos información que si no lo supiera!



Suena complicado, pero si traduces a bandas, entonces todo resulta ser muy simple. $$$H (X | Y)$ Es la información que debemos enviar para informar $$$X$ uno que ya sabe $$$Y$ información en $$$X$ que tampoco está en $$$Y$ . Visualmente, esto significa que $$$H (X | Y)$ - esto es parte de la tira $$$H (X)$ que no se superpone con $$$H (Y)$ .

Ahora puedes leer la desigualdad $$$H (X, Y) ≥H (X) ≥H (X | Y)$ justo en la siguiente tabla.



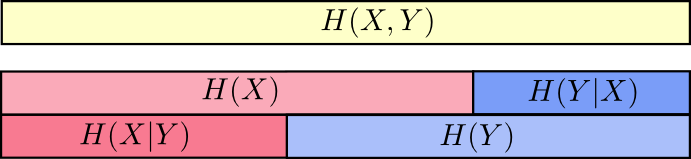
Otra igualdad es la siguiente: $$$H (X, Y) = H (Y) + H (X | Y)$ . Es decir información en $$$X$ y $$$Y$ esta es información en $$$Y$ más información en $$$X$ que no está en $$$Y$ .



Nuevamente, esto es difícil de ver en las ecuaciones, pero fácil de ver si piensas en términos de bandas superpuestas de información.

En este punto, dividimos la información en $$$X$ y $$$Y$ de varias maneras Conocemos la información en cada variable, $$$H (X)$ y $$$H (Y)$ . Conocemos la combinación de información en ambos $$$H (X, Y)$ . Tenemos información que está en una variable pero no en otra, $$$H (X | Y)$ y $$$H (Y | X)$ . Gran parte de esto gira en torno a la información común a las variables: la intersección de su información. Lo llamamos "información mutua" $$$I (x, y)$ definido como:

$$

$$I (X, Y) = H (X) + H (Y) −H (X, Y)$$

Esta definición es verdadera porque $$$H (X) + H (Y)$ contiene dos copias de información mutua, ya que también se encuentra en $$$X$ y en $$$Y$ mientras que $$$H (X, Y)$ contiene solo una copia. (ver diagrama anterior)

La variación de la información está estrechamente relacionada con la información mutua. La variación de información es información que no es común a las variables. Podemos definirlo así:

$$

$$V (X, Y) = H (X, Y) −I (X, Y)$$

La variación de la información es interesante porque nos da una métrica, el concepto de la distancia entre diferentes variables. La variación de información entre dos variables es cero si conocer el valor de una variable le dice el significado de la otra y se hace más grande a medida que se vuelven más independientes.

¿Cómo se relaciona esto con la divergencia KL, que también nos da el concepto de distancia? La divergencia KL es la distancia entre dos distribuciones sobre la misma variable o conjunto de variables. Por el contrario, la variación de información nos da la distancia entre dos variables co-distribuidas. La divergencia de KL es una discrepancia entre distribuciones, una variación de información dentro de una distribución.

Podemos reunir todo en un solo diagrama que vincula todos estos diferentes tipos de información:

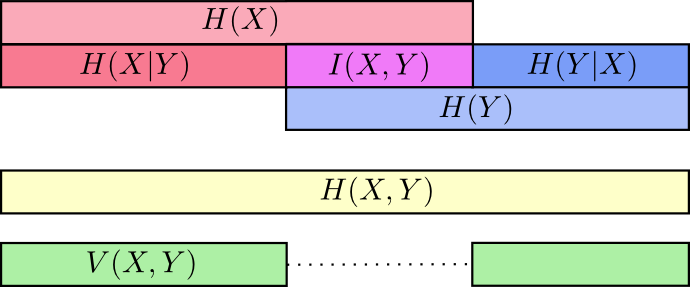
Pedazos de la fracción

Una cosa muy poco intuitiva en la teoría de la información es que podemos tener números fraccionales de bits. Esto es bastante raro ¿Qué significa medio bit?

Aquí hay una respuesta simple: a menudo estamos interesados ​​en la longitud promedio de un mensaje, en lugar de la longitud de un mensaje en particular. Si en la mitad de los casos se envía un bit, y en la mitad de los casos dos, entonces, en promedio, se envían un bit y medio. No hay nada extraño en el hecho de que los promedios pueden ser fraccionarios.

Pero con esta respuesta, rehuimos la pregunta. A menudo, la longitud óptima de las palabras de código también es fraccional. ¿Qué significa esto?

Para ser específicos, veamos la distribución de probabilidad, donde un evento, $$$a$ sucede el 71% de las veces, y otro evento, $$$b$ ocurre el 29% de las veces.



El código óptimo usará 0.5 bit para representar $$$a$ y 1.7 bits para representar $$$b$ . Bueno, si queremos enviar solo una de estas palabras de código, tal representación es imposible. Nos vemos obligados a redondear a un número entero de bits y enviar un promedio de 1 bit.

... Pero si enviamos varios mensajes al mismo tiempo, resulta que podemos hacerlo mejor. Consideremos la transmisión de dos eventos de esta distribución. Si los enviamos de forma independiente, tendríamos que enviar dos bits. ¿Cómo mejoramos esto?



En la mitad de los casos necesitamos enviar $$$aa$ , en el 21% de los casos - $$$ab$ o $$$ba$ , y en el 8% de los casos - $$$bb$ . Una vez más, un código ideal incluye bits fraccionarios.



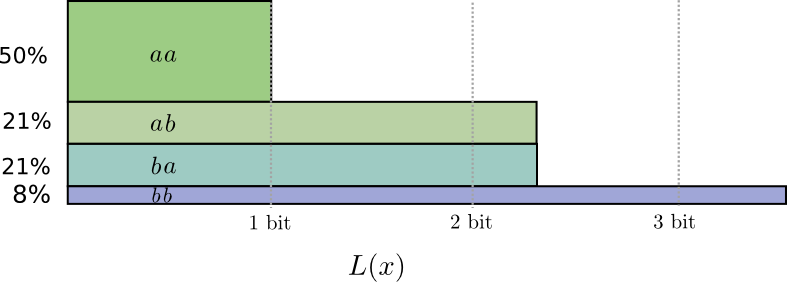
Si redondeamos las longitudes de las palabras de código, obtenemos algo como esto:



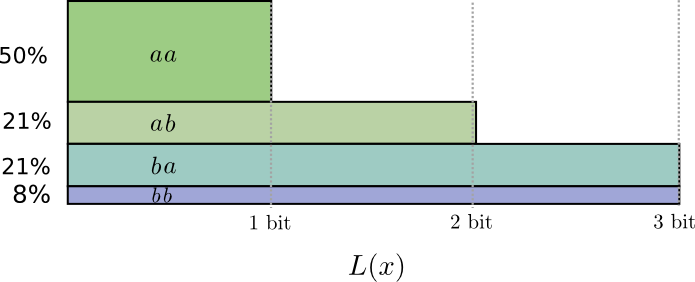
Estos códigos nos dan una longitud promedio de mensaje de 1.8 bits. Esto es menos de 2 bits cuando enviamos mensajes de forma independiente. Es decir En este caso, enviamos 0.9 bits en promedio para cada evento. Si enviamos más eventos a la vez, el promedio sería aún menor. En $$$n$ tendiendo al infinito, la sobrecarga asociada con el redondeo de nuestro código desaparecerá, y el número de bits por palabra de código convergerá a entropía.

A continuación, tenga en cuenta que la longitud ideal de la palabra de código para el evento $$$a$ era 0.5 bit, y la longitud ideal para la palabra de código $$$aa$ - 1 bit. Las longitudes ideales de las palabras de código se suman, ¡incluso si son fraccionarias! Entonces, si reportamos varios eventos a la vez, las longitudes se sumarán.

Como podemos ver, hay un significado real para números fraccionales de bits de información, incluso si los códigos reales solo pueden usar números enteros.

(En la práctica, las personas usan ciertos esquemas de codificación que son efectivos en diferentes casos. El código Huffman, que en realidad es el tipo de código que esbozamos aquí, no maneja bits fraccionarios con mucha elegancia; debe agrupar los caracteres como lo hicimos anteriormente, o usar trucos más complejos para acercarse al límite de la entropía. La codificación aritmética es ligeramente diferente, procesa elegantemente bits fraccionales para ser asintóticamente óptimos).

Conclusión

Si nos preocupa la transferencia de información para el número mínimo de bits, entonces estas ideas son, por supuesto, fundamentales. Si nos preocupa la compresión de datos, la teoría de la información resuelve los problemas principales y nos brinda abstracciones fundamentalmente correctas. Pero, ¿y si no nos importa? ¿No es eso exótico?

Las ideas de la teoría de la información aparecen en muchos contextos: aprendizaje automático, física cuántica, genética, termodinámica e incluso juegos de azar. Los practicantes en estas áreas no se preocupan por la teoría de la información porque quieren comprimir la información. Les importa que tenga una conexión irresistible con su área. El entrelazamiento cuántico puede describirse por entropía. Se pueden obtener muchos resultados en mecánica estadística y termodinámica suponiendo una entropía máxima sobre cosas que usted no sabe. Las ganancias y pérdidas de los jugadores están directamente relacionadas con la divergencia de KL, en particular, las configuraciones iteradas.

La teoría de la información aparece en todos estos lugares porque ofrece formalizaciones concretas y fundamentales para muchas cosas que debemos expresar. Nos da formas de medir y expresar incertidumbre, cuán diferentes son los dos conjuntos de creencias y que la respuesta a una pregunta nos dice sobre la otra: cuán dispersa es la probabilidad, la distancia entre las distribuciones de probabilidad y cuán dependientes son las dos variables. ¿Hay alguna alternativa, ideas similares? Por supuesto Pero las ideas de la teoría de la información son puras, tienen propiedades realmente buenas y se basan en principios. En algunos casos, estas ideas son exactamente lo que necesita, y en otros casos, son un mediador conveniente en un mundo caótico.

El aprendizaje automático es lo que mejor sé, así que hablemos al respecto un minuto. Un tipo de tarea muy común en el aprendizaje automático es la clasificación. Supongamos que queremos ver una imagen y predecir si será una imagen de un perro o un gato.Nuestro modelo puede decir algo como: "Hay un 80% de probabilidad de que se trate de una imagen de un perro, y un 20% de probabilidad de que sea un gato". Supongamos que la respuesta correcta es un perro: cuán buena o mala es lo que dijimos. ¿Qué es un perro 80%? ¿Cuánto mejor diría 85%?

Esta es una pregunta importante porque necesitamos una idea de cuán bueno o malo es nuestro modelo para optimizarlo para el éxito. ¿Qué debemos optimizar? La respuesta correcta en realidad depende de para qué usamos el modelo: ¿solo nos importa si nuestra suposición es correcta o si nos preocupamos de la confianza que tenemos en la respuesta correcta? ¿Qué tan malo es equivocarse con confianza? No hay una única respuesta correcta a esto. Y a menudo es imposible encontrar la respuesta correcta, porque no sabemos exactamente cómo se usará el modelo para formalizar lo que finalmente nos emociona. Hay situaciones en las que la entropía cruzada es exactamente lo que nos preocupa, pero este no es siempre el caso. Más a menudo, no sabemos exactamente lo que nos preocupa, y la entropía cruzada es un buen proxy.

La información nos brinda una nueva base sólida para pensar sobre el mundo. A veces es ideal para una tarea determinada; en otros casos, no del todo, pero sigue siendo extremadamente útil. Este ensayo solo arañó la superficie de la teoría de la información: hay temas básicos, como los códigos de corrección de errores, que no tocamos en absoluto, pero espero haber demostrado que la teoría de la información es un tema maravilloso que no debería ser intimidante.