¿Por qué la clasificación rápida es realmente lenta? Nuevo método de ordenación de matriz

Muchos programadores piensan que Quick Sort es el algoritmo más rápido de todos. Esto es en parte cierto. Pero funciona realmente bien solo si el elemento de soporte está seleccionado correctamente ( entonces la complejidad es O (n log n) ). De lo contrario, el comportamiento asintótico será aproximadamente el mismo que el de la burbuja ( es decir, O (n ² ) ).
Al mismo tiempo, si la matriz ya está ordenada, el algoritmo seguirá funcionando no más rápido que O (n log n)

En base a esto, decidí escribir mi propio algoritmo para ordenar una matriz que funcionaría mejor que quick_sort. Y si la matriz ya está ordenada, no la ejecute muchas veces, como es el caso con muchos algoritmos.

"Era de noche, no había nada que hacer", - Sergei Mikhalkov.

Requisitos:

1. Mejor caso O (n)
2. El caso promedio de O (n log n)
3. Peor caso O (n log n)
4. En promedio más rápido que la clasificación rápida

Ahora vamos a poner todo en orden

Para que nuestro algoritmo funcione siempre rápidamente, es necesario que en el caso promedio el comportamiento asintótico sea al menos O (n log n), y en el mejor de los casos, O (n). Todos sabemos muy bien que, en el mejor de los casos, la clasificación por inserción funciona de una vez. Pero en el peor de los casos, tendrá que conducir alrededor de la matriz tantas veces como haya elementos en ella.

Información preliminar

int* glue(int* a, int lenA, int* b, int lenB) { int lenC = lenA + lenB; int* c = new int[lenC]; //   int indx_a = 0; int indx_b = 0; int i = 0; for (; i < lenC; ++i) { if (indx_a < lenA) { if (indx_b < lenB) { //     c[i] = (a[indx_a] < b[indx_b]) ? a[indx_a++] : b[indx_b++]; continue; } //      while (indx_a < lenA) c[i++] = a[indx_a++]; } else //      while (indx_b < lenB) c[i++] = b[indx_b++]; break; } return c; } 

 void glueDelete(int*& arr, int*& a, int lenA, int*& b, int lenB) { if (lenA == 0) { //    delete[] a; //     arr = b; //     return; } if (lenB == 0) { //    delete[] b; //     arr = a; //     return; } int *copy = glue(a, lenA, b, lenB); //  delete[]a; //    delete[]b; //    arr = copy; //   } 

 void insertionSort(int*& arr, int lo, int hi) { for (int i = lo + 1; i <= hi; ++i) for (int j = i; j > 0 && arr[j - 1] > arr[j]; --j) swap(arr[j - 1], arr[j]); } 

Versión inicial del algoritmo (no óptima):

La idea principal del algoritmo es la llamada búsqueda de máximo (y mínimo). En cada iteración, seleccione un elemento de la matriz. Si es mayor que el máximo anterior, agregue este elemento al final de la selección. De lo contrario, si es menor que el mínimo anterior, entonces agregamos este elemento al principio. De lo contrario, poner en una matriz separada.

La función de entrada toma una matriz y el número de elementos en esta matriz.

 void FirstNewGeneratingSort(int*& arr, int len) 

Para almacenar una muestra de la matriz (nuestras altas y bajas) y otros elementos, asignamos memoria

 int* selection = new int[len << 1]; //     new int[len * 2] int left = len - 1; //       int right = len; //       int* restElements = new int[len]; //  ,      int restLen = 0; //      

Como puede ver, asignamos 2 veces más memoria para almacenar la muestra que nuestra matriz original. Esto se hace en caso de que tengamos una matriz ordenada y cada elemento siguiente sea un nuevo máximo. Entonces solo la segunda parte de la matriz de muestra estará ocupada. O viceversa (si se ordena en orden descendente).

Para muestrear, primero necesita el mínimo y el máximo iniciales. Solo selecciona el primer y segundo elemento

 if (arr[0] > arr[1]) swap(arr[0], arr[1]); selection[left--] = arr[0]; selection[right++] = arr[1]; 

Muestreo en sí

 for (int i = 2; i < len; ++i) { if (selection[right - 1] <= arr[i]) //     { selection[right++] = arr[i]; continue; } if (selection[left + 1] >= arr[i]) //     { selection[left--] = arr[i]; continue; } restElements[restLen++] = arr[i]; //      ,    } 

Ahora tenemos un conjunto ordenado de elementos y los elementos "restantes" que aún tenemos que ordenar. Pero primero debes hacer algo de manipulación de la memoria.

Libere memoria no utilizada

 int selectionLen = right - left - 1; //   int* copy = glue(selection + left + 1, selectionLen, nullptr, 0); //       delete[] selection; //   2 * len ,         ,     selection = copy; //  ,    selection     delete[] arr; //    ,         ,       

Haga una llamada recursiva para los elementos restantes y combínelos con la selección

 FirstNewGeneratingSort(restElements, restLen); glueDelete(arr, selection, selectionLen, restElements, restLen); 

 void FirstNewGeneratingSort(int*& arr, int len) { if (len < 2) return; int* selection = new int[len << 1]; int left = len - 1; int right = len; int* restElements = new int[len]; int restLen = 0; if (arr[0] > arr[1]) swap(arr[0], arr[1]); selection[left--] = arr[0]; selection[right++] = arr[1]; for (int i = 2; i < len; ++i) { if (selection[right - 1] <= arr[i]) //     { selection[right++] = arr[i]; continue; } if (selection[left + 1] >= arr[i]) //     { selection[left--] = arr[i]; continue; } restElements[restLen++] = arr[i]; //      ,    } int selectionLen = right - left - 1; //   int* copy = glue(selection + left + 1, selectionLen, nullptr, 0); //       delete[] selection; //   2 * len ,          ,     selection = copy; //  ,    selection     delete[] arr; //    ,         ,       FirstNewGeneratingSort(restElements, restLen); glueDelete(arr, selection, selectionLen, restElements, restLen); } 

Vamos a ver la velocidad del algoritmo en comparación con la ordenación rápida

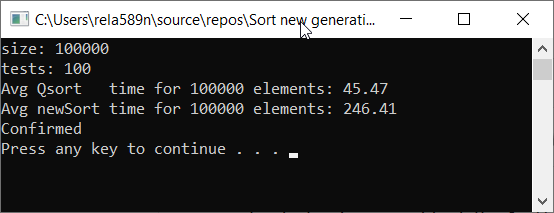
Como puede ver, esto no es lo que queríamos. ¡Casi 6 veces más que QuickSort! Pero, en este contexto, es inapropiado usarlo, ya que aquí es lo asintótico lo que importa. En esta implementación del algoritmo, en el peor de los casos, los elementos primero y segundo serán mínimos y máximos. Y el resto se copiará en una matriz separada.

Complejidad del algoritmo:

• Peor caso: O (n ² )
• Caso medio: O (n ² )
• Mejor caso: O (n)

Hmm, esto no es mejor que la misma clasificación por insertos. Sí, de hecho, podemos encontrar el elemento máximo (mínimo) muy rápidamente, y el resto simplemente no caerá en la selección.

Podemos intentar optimizar la ordenación por fusión. Primero, verifique la velocidad del tipo de fusión habitual:

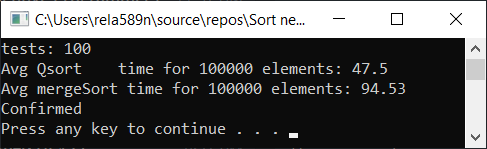
 void newGenerationMergeSort(int* a, int lo, int hi, int& minPortion) { if (hi <= lo) return; int mid = lo + (hi - lo) / 2; if (hi - lo <= minPortion) { //       ,     int* part = glue(a + lo, hi - lo + 1, nullptr, 0); //    FirstNewGeneratingSort(part, hi - lo + 1); for (int i = lo; i <= hi; ++i) { a[i] = part[i - lo]; } delete[] part; return; } newGenerationMergeSort(a, lo, mid, minPortion); newGenerationMergeSort(a, mid + 1, hi, minPortion); int* b = glue(a + lo, mid - lo + 1, a + mid + 1, hi - mid); for (int i = lo; i <= hi; i++) a[i] = b[i - lo]; delete[] b; } 

Se necesita algún tipo de envoltura para facilitar su uso.

 void newMergeSort(int *arr, int length) { int portion = log2(length); //      portion *= portion; newGenerationMergeSort(arr, 0, length - 1, portion); } 

Resultado de la prueba:

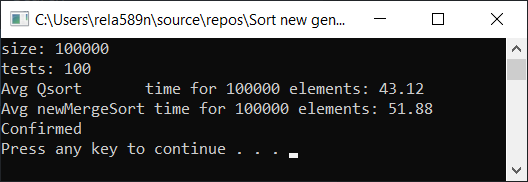
Sí, se observa un aumento en la velocidad, pero, sin embargo, esta función no funciona tan rápido como la Clasificación rápida. Además, no podemos hablar de O (n) en matrices ordenadas. Por lo tanto, esta opción también se descarta.

Opciones de optimización para la primera opción.

1. Para garantizar que la complejidad no sea O (n ² ), podemos agregar elementos que no cayeron en la muestra, no en 1 matriz como antes, sino expandirlos en 2 matrices. Después de eso, solo queda clasificar estas dos partes y fusionarlas con nuestra muestra. Como resultado, obtenemos una complejidad igual a O (n log n)

2. Como ya hemos notado, el elemento absolutamente máximo (mínimo) en la matriz ordenada se puede encontrar con bastante rapidez, y esto no es muy efectivo. Aquí es donde entra la clasificación de inserción para ayudarnos. En cada iteración de la selección, verificaremos si podemos insertar el elemento de flujo en un conjunto de los últimos, por ejemplo, ocho insertados.

Si no está claro ahora, no te enfades. Debería ser así. Ahora todo quedará claro en el código y las preguntas desaparecerán.

La versión correcta residual del algoritmo:

La firma es la misma que en la versión anterior.

 void newGenerationSort(int*& arr, int len) 

Pero debe tenerse en cuenta que esta opción supone un puntero al primer parámetro en el que se puede invocar la operación delete [] (por qué, lo veremos más adelante). Es decir, cuando asignamos memoria, asignamos la dirección del comienzo de la matriz para este puntero.

Preparación preliminar

En este ejemplo, el llamado "coeficiente de recuperación" es solo una constante con un valor de 8. Muestra cuántos elementos máximos intentamos atravesar para insertar un nuevo "submáximo" o "submínimo" en su lugar.

 int localCatchUp = min(catchUp, len); //            insertionSort(arr, 0, localCatchUp - 1); //     localCatchUp  if (len <= localCatchUp) //       n <= catchUp ,   return; //    (      ) 

Para almacenar la muestra, cree una matriz

Si algo no está claro, entonces vea la explicación en la versión inicial

 int* selection = new int[len << 1]; //     new int[len * 2] int left = len - 1; //       int right = len; //       

Complete los primeros elementos de la matriz de selección.

 selection[left--] = arr[0]; for (int i = 1; i < localCatchUp; ++i) { selection[right++] = arr[i]; } 

Permítame recordarle que los nuevos mínimos van al lado izquierdo del centro de la matriz de muestras, y los nuevos máximos van a la derecha

Crear matrices para almacenar elementos no seleccionados

 int restLen = len >> 1; //     len / 2 int* restFirst = new int[restLen]; int* restSecond = new int[restLen]; int restFirstLen = 0; int restSecondLen = 0; 

Ahora, lo más importante es la selección correcta de elementos de la matriz fuente

El ciclo comienza con localCatchUp (porque los elementos anteriores ya han ingresado a nuestra muestra como los valores a partir de los cuales comenzaremos). Y va hasta el final. Entonces, después, al final, todos los elementos se distribuirán en la matriz de selección o en una de las matrices de subselección.

Para verificar si podemos insertar un elemento en la selección, simplemente verificaremos si es más (o igual) a las posiciones del elemento 8 a la izquierda (derecha - localCatchUp). Si este es el caso, simplemente lo insertamos en la posición deseada con una pasada a través de estos elementos. Esto fue para el lado derecho, es decir, para los elementos máximos. Del mismo modo, hacemos lo contrario para los mínimos. Si no puede insertarlo en ninguno de los lados de la selección, lo incluimos en una de las matrices restantes.

El bucle se verá así:

 for (int i = localCatchUp; i < len; ++i) { if (selection[right - localCatchUp] <= arr[i]) { selection[right] = arr[i]; for (int j = right; selection[j - 1] > selection[j]; --j) swap(selection[j - 1], selection[j]); ++right; continue; } if (selection[left + localCatchUp] >= arr[i]) { selection[left] = arr[i]; for (int j = left; selection[j] > selection[j + 1]; ++j) swap(selection[j], selection[j + 1]); --left; continue; } if (i & 1) { // i -  restFirst[restFirstLen++] = arr[i]; } else { restSecond[restSecondLen++] = arr[i]; } } 

De nuevo, ¿qué está pasando aquí? Primero intentamos llevar el elemento a los máximos. No funciona - Si es posible, tíralo a los mínimos. Si es imposible hacer esto también, póngalo en reposo Primero o en segundo lugar.

La parte más difícil ha terminado. Ahora, después del ciclo, tenemos una matriz ordenada con una selección (los elementos comienzan en el índice [left + 1] y finalizan en [right - 1] ), así como las matrices restFirst y restSecond de longitud restFirstLen y restSecondLen, respectivamente.

Como en el ejemplo anterior, antes de la llamada recursiva liberamos la memoria de la matriz principal (ya guardamos todos sus elementos)

 delete[] arr; 

Nuestra matriz de selección puede contener muchas celdas de memoria no utilizada. Antes de una llamada recursiva, debe liberarla.

Libere memoria no utilizada

 int selectionLen = right - left - 1; //     int* copy = glue(selection + left + 1, selectionLen, nullptr, 0); //        delete[] selection; //    2 * len   selection = copy; //      ,   

Ahora ejecute nuestra función de clasificación de forma recursiva para las matrices restFirst y restSecond

Para entender cómo funciona, primero debe mirar el código hasta el final. Por ahora, solo necesita creer que después de las llamadas recursivas, se ordenarán las matrices restFirst y restSecond.

 newGenerationSort(restFirst, restFirstLen); newGenerationSort(restSecond, restSecondLen); 

Y finalmente, necesitamos fusionar 3 matrices en la resultante y asignarla al puntero arr.

Primero puede combinar restFirst + restSecond en una matriz restFull , y luego fusionar selection + restFull . Pero este algoritmo tiene una propiedad tal que lo más probable es que la matriz de selección contenga muchos menos elementos que cualquiera de las demás matrices. Suponga que la selección contiene 100 elementos, restFirst contiene 990 y restSecond contiene 1010. Luego, para crear una matriz restFull , debe realizar 990 + 1010 = 2000 operaciones de copia. Luego, para fusionar con la selección , otras 2000 + 100 copias. Total con este enfoque, la copia total será 2000 + 2100 = 4100.

Apliquemos la optimización aquí. Primero combine la selección y descanse Primero en la matriz de selección . Operaciones de copia: 100 + 990 = 1090. Luego, combine la selección y descanse las segundas matrices y gaste otras 1090 + 1010 = 2100 copias. En total, se lanzarán 2100 + 1090 = 3190, que es casi un cuarto menos que con el enfoque anterior.

La fusión final de matrices

 int* part2; int part2Len; if (selectionLen < restFirstLen) { glueDelete(selection, restFirst, restFirstLen, selection, selectionLen); // selection += restFirst selectionLen += restFirstLen; part2 = restSecond; part2Len = restSecondLen; } else { glueDelete(part2, restFirst, restFirstLen, restSecond, restSecondLen); // part2 = restFirst + restSecond part2Len = restFirstLen + restSecondLen; } glueDelete(arr, selection, selectionLen, part2, part2Len); 

Como puede ver, si nos resulta más rentable fusionar la selección con restFirst , entonces lo hacemos. De lo contrario, nos fusionamos como en "restFull"

 /// works only if arr is pointer assigned by new keyword void newGenerationSort(int*& arr, int len) { int localCatchUp = min(catchUp, len); //            insertionSort(arr, 0, localCatchUp - 1); //     localCatchUp  if (len <= localCatchUp) //       n <= catchUp  return; //      int* selection = new int[len << 1]; //     new int[len * 2] int left = len - 1; //       int right = len; //       selection[left--] = arr[0]; for (int i = 1; i < localCatchUp; ++i) { selection[right++] = arr[i]; } int restLen = len >> 1; int* restFirst = new int[restLen]; int* restSecond = new int[restLen]; int restFirstLen = 0; int restSecondLen = 0; for (int i = localCatchUp; i < len; ++i) { if (selection[right - localCatchUp] <= arr[i]) { selection[right] = arr[i]; for (int j = right; selection[j - 1] > selection[j]; --j) swap(selection[j - 1], selection[j]); ++right; continue; } if (selection[left + localCatchUp] >= arr[i]) { selection[left] = arr[i]; for (int j = left; selection[j] >= selection[j + 1]; ++j) swap(selection[j], selection[j + 1]); --left; continue; } if (i & 1) { // i -  restFirst[restFirstLen++] = arr[i]; } else { restSecond[restSecondLen++] = arr[i]; } } delete[] arr; int selectionLen = right - left - 1; //     int* copy = glue(selection + left + 1, selectionLen, nullptr, 0); //        delete[] selection; //    2 * len   selection = copy; //      ,   newGenerationSort(restFirst, restFirstLen); newGenerationSort(restSecond, restSecondLen); int* part2; int part2Len; if (selectionLen < restFirstLen) { glueDelete(selection, restFirst, restFirstLen, selection, selectionLen); // selection += restFirst selectionLen += restFirstLen; part2 = restSecond; part2Len = restSecondLen; } else { glueDelete(part2, restFirst, restFirstLen, restSecond, restSecondLen); // part2 = restFirst + restSecond part2Len = restFirstLen + restSecondLen; } glueDelete(arr, selection, selectionLen, part2, part2Len); } 

Ahora tiempo de prueba

 #include <iostream> #include <ctime> #include <vector> #include <algorithm> #include "time_utilities.h" #include "sort_utilities.h" using namespace std; using namespace rela589n; void printArr(int* arr, int len) { for (int i = 0; i < len; ++i) { cout << arr[i] << " "; } cout << endl; } bool arraysEqual(int* arr1, int* arr2, int len) { for (int i = 0; i < len; ++i) { if (arr1[i] != arr2[i]) { return false; } } return true; } int* createArray(int length) { int* a1 = new int[length]; for (int i = 0; i < length; i++) { a1[i] = rand(); //a1[i] = (i + 1) % (length / 4); } return a1; } int* array_copy(int* arr, int length) { int* a2 = new int[length]; for (int i = 0; i < length; i++) { a2[i] = arr[i]; } return a2; } void tester(int tests, int length) { double t1, t2; int** arrays1 = new int* [tests]; int** arrays2 = new int* [tests]; for (int t = 0; t < tests; ++t) { //    int* arr1 = createArray(length); arrays1[t] = arr1; arrays2[t] = array_copy(arr1, length); } t1 = getCPUTime(); for (int t = 0; t < tests; ++t) { quickSort(arrays1[t], 0, length - 1); } t2 = getCPUTime(); cout << "Avg Qsort time for " << length << " elements: " << (t2 - t1) * 1000 / tests << endl; int portion = catchUp = 8; t1 = getCPUTime(); for (int t = 0; t < tests; ++t) { newGenerationSort(arrays2[t], length); } t2 = getCPUTime(); cout << "Avg newGenSort time for " << length << " elements: " << (t2 - t1) * 1000 / tests //<< " Catch up coef: "<< portion << endl; bool confirmed = true; //     for (int t = 0; t < tests; ++t) { if (!arraysEqual(arrays1[t], arrays2[t], length)) { confirmed = false; break; } } if (confirmed) { cout << "Confirmed" << endl; } else { cout << "Review your code! Something wrong..." << endl; } } int main() { srand(time(NULL)); int length; double t1, t2; cout << "size: "; cin >> length; int t; cout << "tests: "; cin >> t; tester(t, length); system("pause"); return 0; } 

 // [min, max] int random(int min, int max) { return min + rand() % ((max + 1) - min); } void quickSort(int * arr, int b, int e) { int l = b, r = e; int piv = arr[random(l, r)]; while (l <= r) { for (; arr[l] < piv; ++l); for (; arr[r] > piv; --r); if (l <= r) swap(arr[l++], arr[r--]); } if (b < r) quickSort(arr, b, r); if (e > l) quickSort(arr, l, e); } 

 #pragma once #if defined(_WIN32) #include <Windows.h> #elif defined(__unix__) || defined(__unix) || defined(unix) || (defined(__APPLE__) && defined(__MACH__)) #include <unistd.h> #include <sys/resource.h> #include <sys/times.h> #include <time.h> #else #error "Unable to define getCPUTime( ) for an unknown OS." #endif /** * Returns the amount of CPU time used by the current process, * in seconds, or -1.0 if an error occurred. */ double getCPUTime() { #if defined(_WIN32) /* Windows -------------------------------------------------- */ FILETIME createTime; FILETIME exitTime; FILETIME kernelTime; FILETIME userTime; if (GetProcessTimes(GetCurrentProcess(), &create;Time, &exit;Time, &kernel;Time, &user;Time) != -1) { SYSTEMTIME userSystemTime; if (FileTimeToSystemTime(&user;Time, &user;SystemTime) != -1) return (double)userSystemTime.wHour * 3600.0 + (double)userSystemTime.wMinute * 60.0 + (double)userSystemTime.wSecond + (double)userSystemTime.wMilliseconds / 1000.0; } #elif defined(__unix__) || defined(__unix) || defined(unix) || (defined(__APPLE__) && defined(__MACH__)) /* AIX, BSD, Cygwin, HP-UX, Linux, OSX, and Solaris --------- */ #if defined(_POSIX_TIMERS) && (_POSIX_TIMERS > 0) /* Prefer high-res POSIX timers, when available. */ { clockid_t id; struct timespec ts; #if _POSIX_CPUTIME > 0 /* Clock ids vary by OS. Query the id, if possible. */ if (clock_getcpuclockid(0, &id;) == -1) #endif #if defined(CLOCK_PROCESS_CPUTIME_ID) /* Use known clock id for AIX, Linux, or Solaris. */ id = CLOCK_PROCESS_CPUTIME_ID; #elif defined(CLOCK_VIRTUAL) /* Use known clock id for BSD or HP-UX. */ id = CLOCK_VIRTUAL; #else id = (clockid_t)-1; #endif if (id != (clockid_t)-1 && clock_gettime(id, &ts;) != -1) return (double)ts.tv_sec + (double)ts.tv_nsec / 1000000000.0; } #endif #if defined(RUSAGE_SELF) { struct rusage rusage; if (getrusage(RUSAGE_SELF, &rusage;) != -1) return (double)rusage.ru_utime.tv_sec + (double)rusage.ru_utime.tv_usec / 1000000.0; } #endif #if defined(_SC_CLK_TCK) { const double ticks = (double)sysconf(_SC_CLK_TCK); struct tms tms; if (times(&tms;) != (clock_t)-1) return (double)tms.tms_utime / ticks; } #endif #if defined(CLOCKS_PER_SEC) { clock_t cl = clock(); if (cl != (clock_t)-1) return (double)cl / (double)CLOCKS_PER_SEC; } #endif #endif return -1; /* Failed. */ } 

Todas las pruebas se realizaron en la máquina a un porcentaje. Intel Core i3 7100u y 8 GB de RAM

Matriz completamente aleatoria

 a1[i] = rand(); 

Matriz parcialmente ordenada

 a1[i] = (i + 1) % (length / 4); 

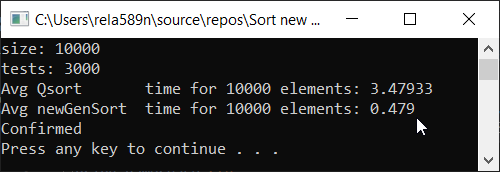
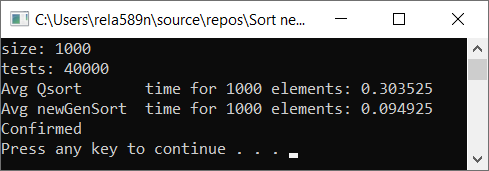
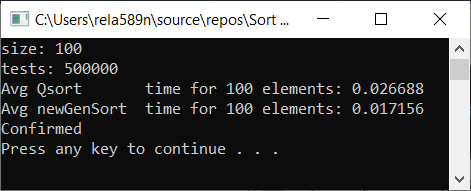
Matriz totalmente ordenada

 a1[i] = (i + 1); 

Conclusiones

Como puede ver, el algoritmo funciona y funciona bien. Al menos todo lo que queríamos se logró. A expensas de la estabilidad, no estoy seguro de no haberlo verificado. Puedes comprobarlo tú mismo. Pero en teoría debería lograrse muy fácilmente. Solo en algunos lugares, en lugar del signo>, ponga ≥ o algo.