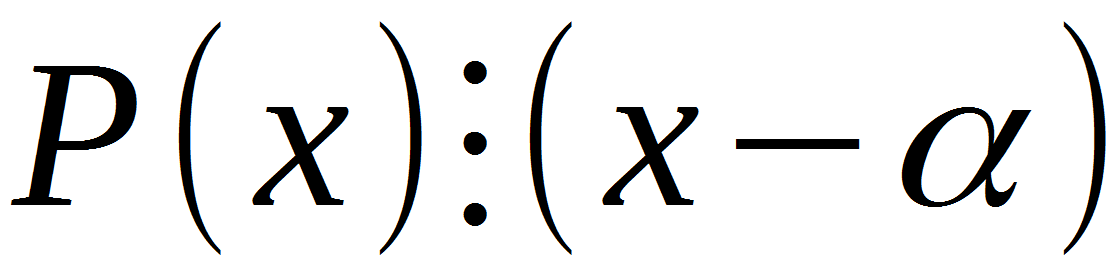
Como regla general, en física, informática y economía, nos enfrentamos con las ecuaciones racionales lineales o fraccionarias más simples, con menos frecuencia con ecuaciones cuadráticas. ¿Y las ecuaciones de tercer y cuarto grado? Si estás interesado, entonces te pido un gato.
Primero, considere el concepto de una ecuación del más alto grado. Una ecuación del grado más alto es una ecuación de la forma:

En este artículo consideraré:
1. Ecuaciones cúbicas.
2. Cubicaje retornable.
3. Aplicación del esquema de Horner y el teorema de Bezout.
4. Ecuaciones biquadraticas retornables.
Ecuaciones cúbicas
Las ecuaciones cúbicas son ecuaciones en las que el grado desconocido es desconocido para el término senior. Las ecuaciones cúbicas tienen la siguiente forma:

Dichas ecuaciones se pueden resolver de diferentes maneras, sin embargo, utilizaremos el conocimiento de la escuela básica y resolveremos la ecuación cúbica mediante el método de agrupación:

En este ejemplo, se utiliza el método de agrupación, agrupamos los dos primeros y los dos últimos miembros, obteniendo paréntesis iguales, nuevamente logramos, obteniendo la ecuación de dos paréntesis.
Entonces, el producto es igual a cero, y solo si al menos uno de los factores es igual a cero, en base a esto equiparamos cada factor (paréntesis) a cero, obteniendo una ecuación cuadrática y lineal incompleta.
También vale la pena señalar que el número máximo de raíces de una ecuación es igual al grado desconocido con el término principal, por lo que en una ecuación cúbica no puede haber más de tres raíces, en una biquadratica (cuarto grado) no más de cuatro raíces y. etc.
Devolver ecuaciones cúbicas
Las ecuaciones cúbicas de retorno tienen la forma:

Se llaman retornables porque los coeficientes se reflejarán. Ecuaciones similares también se resuelven mediante métodos escolares, pero un poco más complicadas:

Primero, se realiza la agrupación, luego, usando las fórmulas de multiplicación abreviada, descomponemos los factores resultantes. Nuevamente obtenemos 2 paréntesis iguales, "los sacamos". Obtenemos dos factores (paréntesis) y los resolvemos como dos ecuaciones diferentes.
El teorema de Bezout y el esquema de Horner
El teorema de Bezout fue descubierto, sorprendentemente, por Etienne Bezout, un matemático francés que se preocupaba principalmente por el álgebra. El teorema de Bezout se puede formular de la siguiente manera:

Vamos a resolverlo. P (x) es cualquier polinomio en x, (x - a) es el binomio en el que a es una de las raíces enteras de la ecuación que encontramos entre los divisores del término libre.
Tres puntos, este es un operador que indica que una expresión se divide por otra. De esto se deduce que habiendo encontrado al menos una raíz de una ecuación dada, podemos aplicarle este teorema. Pero, ¿por qué se necesita este teorema, cuál es su efecto? El teorema de Bezout es una herramienta universal si desea reducir el grado de un polinomio. Por ejemplo, con su ayuda, la ecuación cúbica se puede convertir en un cuadrado, biquadratic, cubic, etc.
Pero una cosa es entender, pero ¿cómo dividir? Por supuesto, puede dividirlo en una columna, pero este método no está disponible para todos y la probabilidad de cometer un error es muy alta. Por lo tanto, hay otra forma, este es el esquema de Horner. Explicaré su trabajo con un ejemplo. Supongamos:

Y así, se nos ha dado un polinomio, y es posible que hayamos encontrado una de las raíces de antemano. Ahora dibujamos una pequeña placa de 6 columnas y 2 filas, en cada columna de la primera fila (excepto la primera), introducimos los coeficientes de la ecuación. Y en la primera columna de la fila 2 agregamos el valor de a (la raíz encontrada). Luego, el primer coeficiente, en nuestro caso 5, simplemente explotamos. Los valores de las siguientes columnas se calculan de la siguiente manera:

(La foto está prestada
aquí )
A continuación, hacemos lo mismo con el resto de las columnas. El valor de la última columna (2 filas) será el resto de la división, en nuestro caso 0, si obtiene un número distinto de 0, entonces debe elegir un enfoque diferente. Un ejemplo para una ecuación cúbica:

Ecuaciones biquadráticas retornables
También consideramos las ecuaciones cúbicas de retorno anteriores, y ahora analizamos las ecuaciones biquadráticas. Su visión general:

A diferencia de la ecuación de retorno cúbico, no todos tienen un par biquadratico con respecto a los coeficientes, pero por lo demás son muy similares. Aquí está el algoritmo para resolver tales ecuaciones:

Como puede ver, resolver tales ecuaciones no es para nada simple. Pero voy a distinguir este caso de todos modos. La solución comienza dividiendo la ecuación completa por x ^ 2. A continuación, agrupamos, aquí introduje específicamente una línea adicional para mayor claridad. Después de eso, hacemos el truco e ingresamos en el primer paréntesis 2, que primero sumamos y luego restamos, la cantidad no cambiará de todos modos, pero ahora podemos doblar este paréntesis en el cuadrado de la suma.
Eliminamos -2 del paréntesis, primero multiplicándolo por a, después de lo cual introducimos una nueva variable, t, y obtenemos la ecuación cuadrática.
Ahora pasemos a un ejemplo:

La parte principal, como en el algoritmo generalizado, se divide por x ^ 2, agrupada, colapsada en un cuadrado completo, realizamos una sustitución de variables y resolvemos la ecuación cuadrática. Después de eso, sustituimos las raíces obtenidas y resolvemos 2 ecuaciones cuadráticas más (multiplicadas por x).
Campo de aplicación
Debido a su volumen y especificidad, las ecuaciones de grados superiores rara vez encuentran su aplicación. Sin embargo, todavía hay ejemplos, la ecuación de Poisson para procesos adiabáticos en Física.
Conclusión
En este artículo, consideré solo ecuaciones cúbicas y bicuadráticas. Sin embargo, el teorema de Bezout considerado (y el esquema de Horner) se puede usar para resolver ecuaciones de 5, 6, 7 y otros grados, aunque su aplicación sea limitada.