Modelado GPR

Georadar (dispositivo radio-técnico de sondeo subsuperficial, GPR, Ground Penetrating Radar), que actualmente se usa ampliamente, desde mapear madrigueras de conejos y estudiar lagartijas hasta buscar minas , sigue siendo un placer bastante costoso.


Pantalla GPR (fotograma del programa de televisión británico "Command of the Time")

Pero es posible evaluar sus capacidades y estudiar varios aspectos de la interacción del campo electromagnético del georadar con el medio ambiente sin adquirir / alquilar un dispositivo "de hierro". El paquete gprMax ( gpr - de la abreviatura GPR, Max - las letras iniciales del nombre de James Clerk Maxwell, quien sentó las bases de la electrodinámica), distribuido bajo la licencia GNU GPL v3, nos ayudará.
Los autores de este proyecto, iniciado en 1996, son Craig Warren de la Universidad de Northumbria y Antonis Giannopoulos de la Universidad de Edimburgo. El paquete se desarrolló originalmente en C y luego se reescribió por completo en combinaciones de Python 3 / Cython.


La instalación del paquete requiere compiladores instalados que admitan OpenMP (herramientas de compilación de Microsoft Visual C ++ 2015 (se recomienda esta versión) para Windows / gcc para Linux), la biblioteca NumPy y el compilador de Cython. Después de descargar desde el repositorio en GitHub y desempacar el código fuente del proyecto, vaya a la carpeta raíz y ejecute los comandos:

python setup.py build python setup.py install 

Como "inicio rápido", consideramos trabajar con el paquete usando un ejemplo bidimensional simple: la antena transmisora ​​T de un radar pulsado (impulso GPR) emite un pulso electromagnético, parte de la energía de la cual llega directamente a la antena receptora R en forma de onda directa (DW - onda directa), y algo penetra a través de la arena, se refleja desde la superficie del cilindro conductor y llega a la antena receptora en forma de onda reflejada (RW - onda reflejada):


Formato de archivo de entrada
Cree la carpeta de modelos en la carpeta raíz del proyecto, en la que colocamos el archivo de texto hello.in que contiene los comandos para realizar la simulación (los siguientes comandos corresponden a la versión actual (tercera) del proyecto).

Cada equipo tiene la forma:

 #: _1 _2 _3 ... 

Solo se puede escribir un comando en una línea, y el primer carácter de la línea que contiene el comando debe ser #.

Los comandos pueden ir acompañados de comentarios:

 ## 

El orden de los comandos es importante para los comandos para construir objetos; estos comandos se ejecutan en el orden en que aparecen en el archivo de entrada.

Forma de pulso

Un pulso electromagnético emitido por un georadar dura unas pocas fracciones de nanosegundo, además, tres formas de pulso se usan con mayor frecuencia:

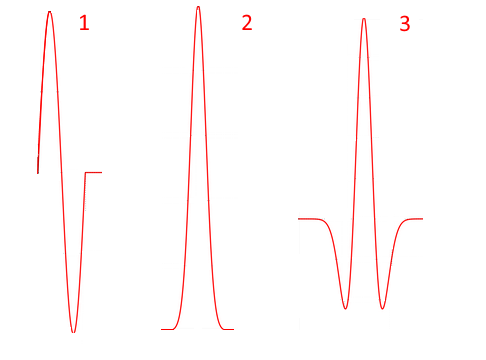
1. un período de onda sinusoidal (seno)
2. Impulso gaussiano (gaussiano)
3. El sombrero mexicano (ricker) es proporcional a la segunda derivada de la función gaussiana, la forma curva de tal impulso se asemeja a un sombrero (esta forma de impulso fue utilizada por el geofísico estadounidense Norman Ricker en 1953 para estudiar señales sísmicas)
   

Para nuestro ejemplo, seleccionamos un pulso gaussiano (tipo de pulso - gaussiano) con una frecuencia central $$$f_c = 1 \\ GHz = 1 \ cdot 10 ^ 9 Hz$ definido por el comando:

 #waveform: gaussian 1 1e9 pulse 

(1 - amplitud de pulso condicional, pulso - etiqueta de pulso)

En este caso, el impulso utilizado en la simulación se describe mediante la expresión:

$$

$$W (t) = e ^ {- 2 \ cdot {\ pi} ^ 2 \ cdot {f_c} ^ 2 {(t- {1 \ over {f_c}})} ^ 2}$$

Modelo de entorno y sistema de coordenadas.

En el modelado 2D, el área estudiada se divide en celdas de un tamaño dado, y el sistema de coordenadas del modelo se ve así: los ejes X e Y forman el plano calculado (con un ancho $$$w$ y alto $$$h$ ), la longitud del modelo a lo largo del eje Z tiene un valor igual al paso de muestreo $$$\ Delta$ .


Al elegir un paso de muestreo, puede seguir la regla general: el tamaño del paso no debe exceder una décima parte de la longitud de onda más pequeña estudiada en el modelo ("10 celdas por longitud de onda"):

$$

$$\ Delta \ le 0,1 \ cdot {\ lambda} _ {min}$$

Para determinar la longitud de onda, es necesario conocer la frecuencia máxima que se tiene en cuenta en el espectro de la señal emitida y la velocidad de la onda en el medio considerado.

La velocidad de propagación de una onda electromagnética en un medio con constante dieléctrica relativa $$${\ epsilon} _r$ , expresado en centímetros por nanosegundo: la unidad de velocidad adoptada en el radar está determinada por la expresión:

$$

$$v = {30 \ over {\ sqrt {{\ epsilon} _r}}}$$

La longitud de onda en centímetros está determinada por la expresión:

$$

$$\ lambda = {v \ over f}$$

( $$$f$ - frecuencia en GHz).
Para mostrar la forma del pulso gaussiano y su espectro, puede usar el comando:

 python -m tools.plot_source_wave gaussian 1 1e9 5e-9 1e-12 -fft 

(gaussiano - tipo de pulso, 1 - amplitud de pulso, 1e9 - frecuencia central (1 GHz), 5e-9 - duración de visualización de pulso (5 ns), 1e-12 - paso de tiempo (1 ps))


Según el espectro de un pulso gaussiano con $$$f_s = 1 \ GHz$ determinar que a -40 dB la frecuencia $$$f \ aproximadamente 3 \ GHz$ .
En este ejemplo, el medio en el que se encuentra el objeto sondeado, seleccionamos arena seca con una permitividad relativa $$${\ epsilon} _r = 3$ .
Encuentre la velocidad de propagación de la onda electromagnética en la arena:

$$

$$v = {30 \ over {\ sqrt {3}}} = 17.3 \ cm / ns$$

Defina la longitud de onda en la arena:

$$

$$\ lambda = {v \ over f} = {17.3 \ over {3}} = 5.8 cm = 58 mm$$

En base a esto, seleccionamos el paso que es el mismo para todos los ejes ( $$$\ Delta = {\ Delta} _x = {\ Delta} _y = {\ Delta} _z$ ) e igual a 2 mm = 0.002 m por razones de conveniencia (un número entero de pasos cabe en 1 cm):

 #dx_dy_dz: 0.002 0.002 0.002 

Limite el área simulada a un rectángulo de ancho $$$w$ igual a 80 cm = 0.8 my altura $$$h$ igual a 60 cm = 0.6 m:

 #domain: 0.60 0.60 0.002 

(para un modelo bidimensional, se requiere indicar un grosor igual a un paso (0.002))

El tamaño del área de simulación y el tamaño del paso espacial determinan el número de celdas del modelo y, en consecuencia, los requisitos de memoria de la computadora.

Describimos la arena con conductividad específica. $$$\ sigma = 0.01 \ \ cm / m$ y constante dieléctrica relativa $$${\ epsilon} _r = 3$ comando:

 #material: 3 0.01 1 0 sand 

(1 corresponde a la permeabilidad magnética relativa $$${\ mu} _r$ igual a la unidad (sin propiedades magnéticas), 0 - sin pérdida magnética y arena - etiqueta de este material).

Llene la arena con la mayor parte del área simulada (de y = 0 a y = 38 cm = 0.38 m):

 #box: 0 0 0 0.80 0.38 0.002 sand 

(0 0 0 - coordenadas de la esquina inferior izquierda, 0.80 0.38 0.002 - coordenadas de la esquina superior derecha (0.002 - paso de muestreo))
El resto es espacio libre (etiqueta free_space), casi equivalente en propiedades de aire ( $$${\ epsilon} _r = 1$ , $$${\ mu} _r = 1$ , $$${\ sigma} = 0$ )
Los límites del área de simulación se presentan como Condición de límite absorbente (ABC).

Como objetivo, elegimos un cilindro de un conductor ideal (que refleje completamente la radiación electromagnética) con un radio de 6 cm = 0.06 m con un centro ubicado en un punto con coordenadas x = 25 cm = 0.25 myy = 10 cm = 0.1 m:

 #cylinder: 0.250 0.1 0 0.250 0.1 0.002 0.06 pec 

(pec es un material perfectamente conductor)

Antenas

El GPR simulado está equipado con dos antenas: transmisión y recepción.
En nuestro estudio de caso, imagine una antena transmisora ​​con un dipolo de Hertz cuya longitud es igual al paso de muestreo (en el caso tridimensional, puede seleccionar una antena de una biblioteca extensa) acostada en la arena (trabajando en contacto con el medio sondeado) a una distancia de 5 cm a la izquierda del centro de la región (x = 35 cm = 0,35 m, y = 38 cm = 0,38 m):

 #hertzian_dipole: z 0.35 0.380 0.0 pulse 

(z es el eje de polarización dipolar (para el caso bidimensional (modo 2D TMz) solo z es válido), el pulso es la etiqueta de la forma del pulso irradiado por la antena)

La antena receptora generalmente se encuentra a una pequeña distancia constante de la recepción, que se denomina la base de la unidad de antena (esta opción para la posición relativa de las antenas se denomina "desplazamiento común"). Como base, seleccione una distancia de 10 cm, de modo que la coordenada horizontal sea 35 + 10 = 45 cm = 0,45 m (5 cm a la derecha del centro de la región):

 #rx: 0.45 0.38 0.0 

Intervalo de simulación

La elección de la ventana de tiempo para el modelado se determina de modo que la señal reflejada desde el objetivo tenga tiempo para llegar a la antena receptora.

Determinamos el tiempo aproximado requerido por la señal en el caso en consideración, tomando la distancia desde las antenas hasta el objetivo $$$h = 18 \ \ cm$ :
$$$t \ approx {2 \ cdot h \ over {v}} = {2 \ cdot 18 \ over 17.3} = 2.1 \ \ ns$
Dado que la parte superior del pulso gaussiano del radar con una frecuencia central de 1 GHz se desplaza en relación con el comienzo del eje de tiempo en 1 ns, seleccionamos una ventana de tiempo de 5 nanosegundos:

 #time_window: 5e-9 

Modelado

Por lo tanto, el contenido del archivo de entrada es el siguiente:


Comenzamos el proceso de modelado:

 python -m gprMax models\hello.in 

Para realizar la simulación, se utiliza el método de dominio de tiempo de diferencia finita (FDTD, dominio de tiempo de diferencia finita) (el algoritmo básico del método fue propuesto por Kane Yee), después de lo cual las células en las que se divide el modelo se denominan células Yee. . Se obtiene una solución numérica en el dominio del tiempo resolviendo las ecuaciones de Maxwell para cada celda.

En el caso bidimensional (modo 2D TMz), solo se calcula el componente $$$E_z$ campo eléctrico y componentes $$$H_x$ y $$$H_y$ campo magnético

Si se excede la cantidad de memoria disponible, se emite un mensaje sobre la falta de memoria para realizar la simulación:


Si alguno de los objetos está fuera del alcance de la simulación, se muestra un mensaje de error:


Para realizar la simulación con el modelo descrito, solo se necesitaron aproximadamente 56 MB de RAM (si reduce el paso a la mitad, hasta 1 mm, los requisitos de memoria aumentan a 99 MB).

Una vez completada la simulación, el archivo hello.out aparece en la carpeta de modelos , que contiene los resultados de la simulación en formato HDF5 , especialmente diseñado para almacenar datos numéricos.

Pista de construcción

Para visualizar los resultados, construimos los rastros:

 python -m tools.plot_Ascan models\hello.out 

Cada pista (exploración A) presentada en la ventana que se abre muestra un gráfico de tiempo de uno de los componentes del campo electromagnético en la ubicación de la antena receptora:


Una onda directa que viene directamente de la antena transmisora ​​(DW) y una onda reflejada desde el objetivo (RW) son visibles en los caminos.

El eje horizontal del tiempo está relacionado con la profundidad del objetivo que refleja la señal a través de la velocidad de la onda electromagnética en la sustancia.

Pero, ¿qué sucede si coloca el comando del cilindro delante del comando de cuadro en el archivo de entrada?


La señal reflejada por el cilindro desapareció: la arena absorbió el cilindro (este es un ejemplo de la importancia del orden en que se construyen los objetos).

Construcción de perfiles

Pero más informativo es el radarograma (radargrama) - perfil (B-scan), que es una combinación de muchas pistas construidas al mover el georadar a lo largo de una dirección determinada; este es el mismo procedimiento para mover un carro con un radar a lo largo del área estudiada.

Cambie la descripción de las antenas moviéndolas al comienzo del eje horizontal:

 #hertzian_dipole: z 0.10 0.38 0.0 pulse #rx: 0.20 0.38 0.0 

Establecemos el paso para mover las antenas igual a 1 cm = 0.01 m:

 #src_steps: 0.01 0 0 #rx_steps: 0.01 0 0 

Por lo tanto, el contenido del archivo de entrada es el siguiente:


Ejecute la simulación en modo por lotes:

 python -m gprMax models\hello.in -n 50 

(50 es el número de pasos que mueve el radar).

Después de comenzar, la simulación se realiza secuencialmente para 50 posiciones GPR:


Después del final de la simulación, hay 50 archivos hello1.out ... hello50.out en la carpeta del modelo.
Combine estos archivos en el archivo hello_merged.out con el comando:

 python -m tools.outputfiles_merge models/hello 

Crea un perfil:

 python -m tools.plot_Bscan models\hello_merged.out Ez 

(Ez es el componente del campo electromagnético mediante el cual construimos el perfil, el componente directamente convertido a voltaje)


Como puede ver, la barra horizontal causada por la onda directa se muestra en el perfil de arriba, y la hipérbola característica causada por la onda reflejada y que muestra el cambio en la distancia del objetivo al GPR cuando se mueve se muestra a continuación.

La leyenda de la derecha muestra los colores coincidentes y las intensidades de campo. $$$E_z$ (se muestra en la pista):
rojo $$$E_z> 0$
blanco $$$E_z = 0$
azul $$$E_z <0$
Al analizar tales perfiles, podemos sacar conclusiones sobre la profundidad, el tamaño e incluso la forma de los objetivos, y las redes neuronales también se utilizan para esto.


Rutas y perfil en la pantalla GPR (fotograma del programa de televisión británico "Command of the Time")

Pero la reflexión se produce no solo a partir de objetos conductores, sino también en el límite de dos capas con diferentes constantes dieléctricas.

Cree una segunda capa de arena con constante dieléctrica en la parte inferior del modelo. $$${\ epsilon} _r = 9$ :



Como se puede ver, debajo de la "traza" de la onda directa (DW), apareció un segmento lineal de la onda (RW) reflejado desde la interfaz de las dos capas de arena.

Fuera del alcance de este ejemplo, las características de gprMax, como el modelado tridimensional, formas de superficie complejas, modelos detallados de antenas, que explican la dispersión de las ondas electromagnéticas ... Además, el paquete se puede usar no solo para simular el GPR, sino también para estudiar la propagación de ondas electromagnéticas en diversos entornos, y Acelere los cálculos con la tecnología NVIDIA CUDA , que proporciona un aumento de diez veces en velocidad en comparación con la computación paralela en una CPU que usa OpenMP. Para aumentar la flexibilidad del modelado, puede colocar bloques de código en Python en el archivo de entrada.

Algunos ejemplos de uso del paquete gprMax:

• evaluación del efecto de las propiedades del suelo sobre la efectividad de GPR en la búsqueda de minas antipersonal
• Comprobando la posibilidad de utilizar un radar de penetración en el suelo para la determinación no destructiva de la profundidad de siembra de semillas de maíz
• Mejorar la calidad de interpretación de los datos de campo de GPR en el estudio de la resistencia de las estructuras de los pasajes subterráneos a través de la carretera.
• Estudio de la relación entre la amplitud de la señal reflejada y el diámetro de las barras de refuerzo en concreto.
• evaluación de la idoneidad de GPR para detectar huecos en troncos de árboles

Enlaces utiles:

Sitio oficial de gprMax
Guía del usuario de GprMax
gprMax en YouTube