
En Serokell, no solo nos dedicamos a proyectos comerciales, sino que también nos esforzamos por mejorar el mundo. Por ejemplo, estamos trabajando para mejorar la herramienta principal de todos los Haskelists: el Glasgow Haskell Compiler (GHC). Nos centramos en ampliar el sistema de tipos bajo la influencia del trabajo de Richard Eisenberg, "Tipos dependientes en Haskell: teoría y práctica" .
En nuestro blog, Vladislav ya habló sobre por qué Haskell carece de tipos dependientes y cómo planeamos agregarlos. Decidimos traducir esta publicación al ruso para que tantos desarrolladores como sea posible pudieran usar tipos dependientes y hacer una contribución adicional al desarrollo de Haskell como idioma.
Estado actual de las cosas
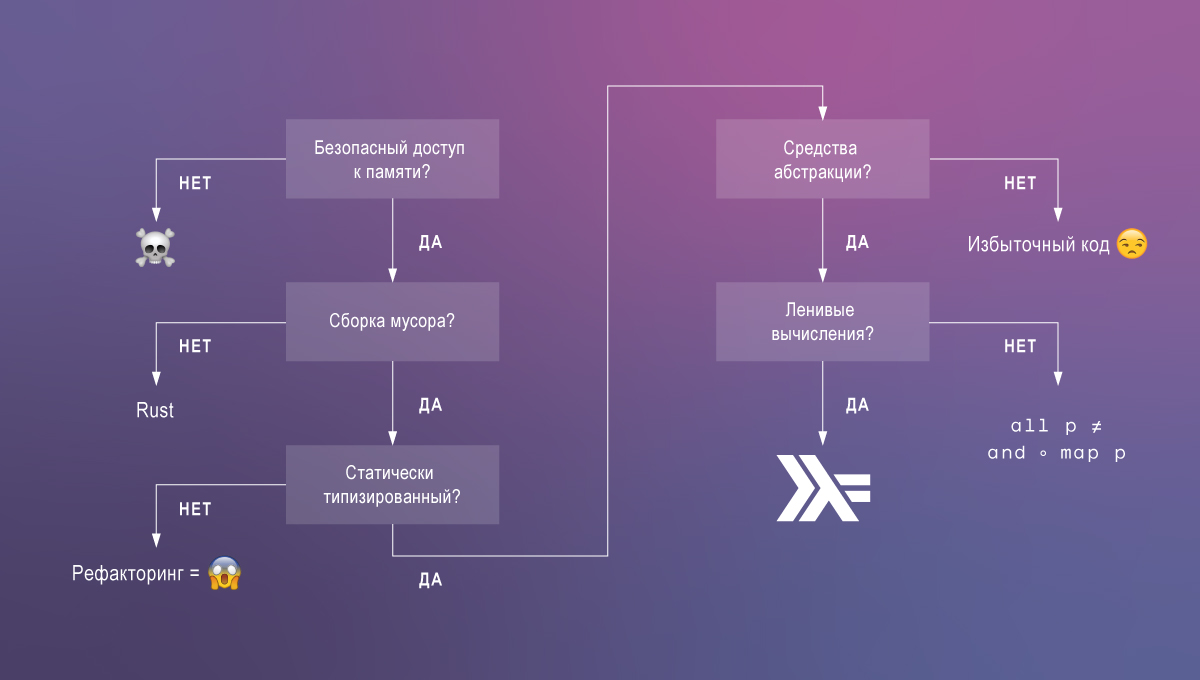
Los tipos dependientes son lo que más extraño en Haskell. Discutamos por qué. Del código que queremos:
- rendimiento, es decir, velocidad de ejecución y bajo consumo de memoria;
- mantenibilidad y facilidad de comprensión;
- corrección garantizada por el método de compilación.
Con las tecnologías existentes, rara vez es posible lograr las tres características, pero con el soporte para los tipos dependientes de Haskell, la tarea se simplifica.
Haskell Standard: Ergonomía + Rendimiento
Haskell se basa en un sistema simple: un cálculo lambda polimórfico con cálculos perezosos, tipos de datos algebraicos y clases de tipos. Es esta combinación de características del lenguaje la que nos permite escribir código elegante, compatible y al mismo tiempo productivo. Para fundamentar esta afirmación, comparamos brevemente Haskell con idiomas más populares.
Los lenguajes con acceso inseguro a la memoria, como C, conducen a los errores y vulnerabilidades más graves (por ejemplo, desbordamientos de búfer, pérdidas de memoria). A veces se necesitan tales lenguajes, pero la mayoría de las veces su uso es una idea más o menos.
Los lenguajes de acceso a la memoria segura forman dos grupos: aquellos que dependen del recolector de basura y Rust. Rust parece ser único en ofrecer acceso seguro a la memoria sin recolección de basura . Tampoco se admiten Cyclone y otros lenguajes de investigación en este grupo. Pero a diferencia de ellos, Rust está en camino a la popularidad. La desventaja es que, a pesar de la seguridad, la administración de memoria de Rust no es trivial y manual. En aplicaciones que pueden permitirse el uso del recolector de basura, es mejor pasar el tiempo de los desarrolladores en otras tareas.
Quedan idiomas con los recolectores de basura, que dividiremos en dos categorías según su sistema de tipos.
Los lenguajes de tipo dinámico (o más bien monotipados ), como JavaScript o Clojure, no proporcionan un análisis estático y, por lo tanto, no pueden proporcionar el mismo nivel de confianza en la corrección del código (y no, las pruebas no pueden reemplazar los tipos; necesita ambos) !).
Los lenguajes de tipo estático como Java o Go a menudo tienen un sistema de tipos muy limitado. Esto obliga a los programadores a escribir código redundante y poner características de lenguaje inseguras. Por ejemplo, la falta de tipos genéricos en Go obliga al uso de la interfaz {} y la conversión de tipos de tiempo de ejecución . Tampoco hay separación entre los cálculos con efectos secundarios (entrada, salida) y los cálculos puros.
Finalmente, entre los idiomas con acceso seguro a la memoria, un recolector de basura y un potente sistema de tipos, Haskell destaca por la pereza. La computación diferida es extremadamente útil para escribir código composable y modular. Permiten descomponer en definiciones auxiliares cualquier parte de las expresiones, incluidas las construcciones que definen un flujo de control.
Haskell parece un lenguaje casi perfecto hasta que te das cuenta de cuán lejos está de liberar todo su potencial en términos de verificación estática en comparación con las herramientas de prueba de teoremas como Agda .
Como un ejemplo simple de dónde el sistema de tipo Haskell no es lo suficientemente potente, considere el operador de indexación de lista de Prelude (o indexar una matriz de un paquete primitive ):
(!!) :: [a] -> Int -> a indexArray :: Array a -> Int -> a
Nada en estas firmas tipo refleja el requisito de que el índice debe ser no negativo y menor que la longitud de la colección. Para software con requisitos de alta confiabilidad esto es inaceptable.
Agda: ergonomía + corrección
Los medios de prueba de teoremas (por ejemplo, Coq ) son herramientas de software que permiten usar una computadora para desarrollar pruebas formales de teoremas matemáticos. Para un matemático, usar tales herramientas es como escribir evidencia en papel. La diferencia en el rigor sin precedentes requerido por una computadora para establecer la validez de dicha evidencia.
Para el programador, sin embargo, los medios para probar los teoremas no son tan diferentes del compilador para el lenguaje de programación esotérico con un sistema de tipo increíble (y posiblemente un entorno de desarrollo integrado) y mediocre (o incluso ausente) todo lo demás. Una forma de probar los teoremas es, de hecho, los lenguajes de programación, cuyos autores dedicaron todo su tiempo a desarrollar un sistema de mecanografía y olvidaron que los programas aún deben ejecutarse.
El preciado sueño de los desarrolladores de software verificados es un medio de probar teoremas, que sería un buen lenguaje de programación con generador de código y tiempo de ejecución de alta calidad. En esta dirección, incluidos los creadores de Idris experimentaron. Pero este es un lenguaje con cálculos estrictos (enérgicos), y su implementación en este momento no es estable.
Entre todos los medios para probar los teoremas, los Haskelistas de Agda son de su agrado. En muchos sentidos, es similar a Haskell, pero con un sistema de tipos más potente. En Serokell lo usamos para probar las diversas propiedades de nuestros programas. Mi colega Dania Rogozin escribió una serie de artículos sobre esto.
Aquí hay un tipo de función de búsqueda similar al operador de Haskell (!!) :
lookup : ∀ (xs : List A) → Fin (length xs) → A
El primer parámetro aquí es de tipo List A , que corresponde a [a] en Haskell. Sin embargo, le damos el nombre xs para referirnos al resto de la firma de tipo. En Haskell, podemos acceder a los argumentos de la función solo en el cuerpo de la función en el nivel de término:
(!!) :: [a] -> Int -> a
Pero en Agda, podemos referirnos a este valor xs en el nivel de tipo, lo que hacemos en el segundo parámetro de lookup , Fin (length xs) . Una función que se refiere a su parámetro en el nivel de tipo se denomina función dependiente y es un ejemplo de tipos dependientes.
El segundo parámetro en la lookup es del tipo Fin n para n ~ length xs . Un valor de tipo Fin n corresponde a un número en el rango [0, n) , por lo que Fin (length xs) es un número no negativo menor que la longitud de la lista de entrada. Esto es exactamente lo que necesitamos para presentar un índice válido de un elemento de la lista. En términos generales, la lookup ["x","y","z"] 2 pasará la verificación de tipo, pero la lookup ["x","y","z"] 42 fallará.
Cuando se trata de ejecutar programas Agda, podemos compilarlos en Haskell utilizando el backend MAlonzo. Pero el rendimiento del código generado será insatisfactorio. Esto no es culpa de MAlonzo: tiene que insertar numerosos unsafeCoerce para que el GHC unsafeCoerce código ya verificado por Agda. Pero el mismo unsafeCoerce reduce el rendimiento (después de la discusión de este artículo, resultó que los problemas de rendimiento pueden haber sido causados por otras razones: nota del autor) .
Esto nos coloca en una posición difícil: tenemos que usar Agda para el modelado y la verificación formal, y luego volver a implementar la misma funcionalidad en Haskell. Con esta organización de flujos de trabajo, nuestro código Agda actúa como una especificación verificada por computadora. Esto es mejor que la especificación en lenguaje natural, pero lejos de ser ideal. El objetivo es que si se compila el código, funcionará de acuerdo con la especificación.
Haskell con extensiones: corrección + rendimiento

Con el objetivo de obtener garantías estáticas de idiomas con tipos dependientes, GHC ha recorrido un largo camino. Se le agregaron extensiones para aumentar la expresividad del sistema de tipos. Empecé a usar Haskell cuando GHC 7.4 era la última versión del compilador. Incluso entonces, tenía las extensiones principales para la programación avanzada a nivel de tipo: RankNTypes , GADTs , TypeFamilies , DataKinds y PolyKinds .
Sin embargo, todavía no hay tipos dependientes completos en Haskell: ni funciones dependientes (tipos Π) ni pares dependientes (tipos Σ). Por otro lado, ¡al menos tenemos una codificación para ellos!
Las prácticas actuales son las siguientes:
- codificar funciones de nivel de tipo como familias de tipos privadas,
- utilizar funcionalización para habilitar funciones no saturadas,
- cerrar la brecha entre términos y tipos utilizando tipos únicos.
Esto conduce a una cantidad significativa de código redundante, pero la biblioteca de singletons automatiza su generación a través de Template Haskell.
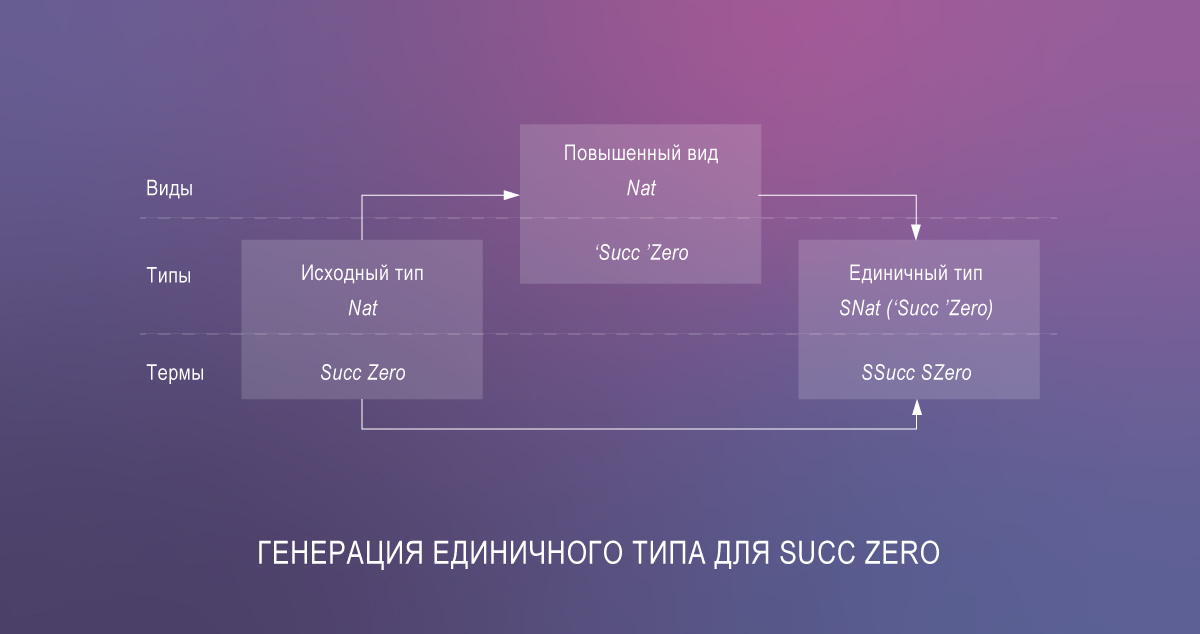
Entonces, el más atrevido y decisivo puede codificar tipos dependientes en Haskell en este momento. Como demostración, aquí hay una implementación de la función de lookup similar a la variante en Agda:
{-# OPTIONS -Wall -Wno-unticked-promoted-constructors -Wno-missing-signatures #-} {-# LANGUAGE LambdaCase, DataKinds, PolyKinds, TypeFamilies, GADTs, ScopedTypeVariables, EmptyCase, UndecidableInstances, TypeSynonymInstances, FlexibleInstances, TypeApplications, TemplateHaskell #-} module ListLookup where import Data.Singletons.TH import Data.Singletons.Prelude singletons [d| data N = Z | SN len :: [a] -> N len [] = Z len (_:xs) = S (len xs) |] data Fin n where FZ :: Fin (S n) FS :: Fin n -> Fin (S n) lookupS :: SingKind a => SList (xs :: [a]) -> Fin (Len xs) -> Demote a lookupS SNil = \case{} lookupS (SCons x xs) = \case FZ -> fromSing x FS i' -> lookupS xs i'
Y aquí hay una sesión de GHCi que muestra que las búsquedas de hecho rechazan los índices que son demasiado grandes:
GHCi, version 8.6.2: http://www.haskell.org/ghc/ :? for help [1 of 1] Compiling ListLookup ( ListLookup.hs, interpreted ) Ok, one module loaded. *ListLookup> :set -XTypeApplications -XDataKinds *ListLookup> lookupS (sing @["x", "y", "z"]) FZ "x" *ListLookup> lookupS (sing @["x", "y", "z"]) (FS FZ) "y" *ListLookup> lookupS (sing @["x", "y", "z"]) (FS (FS FZ)) "z" *ListLookup> lookupS (sing @["x", "y", "z"]) (FS (FS (FS FZ))) <interactive>:5:34: error: • Couldn't match type ''S n0' with ''Z' Expected type: Fin (Len '["x", "y", "z"]) Actual type: Fin ('S ('S ('S ('S n0)))) • In the second argument of 'lookupS', namely '(FS (FS (FS FZ)))' In the expression: lookupS (sing @["x", "y", "z"]) (FS (FS (FS FZ))) In an equation for 'it': it = lookupS (sing @["x", "y", "z"]) (FS (FS (FS FZ)))
Este ejemplo muestra que la viabilidad no significa práctica. Me alegra que Haskell tenga capacidades de lenguaje para implementar lookupS , pero al mismo tiempo me preocupa la complejidad innecesaria que surge. Fuera de los proyectos de investigación, no recomendaría ese estilo de código.
En este caso particular, podríamos lograr el mismo resultado con menos complejidad usando vectores indexados en longitud. Sin embargo, la traducción directa de código de Agda revela mejor los problemas que debe tener en otras circunstancias.
Aquí hay algunos de ellos:
- La relación de escritura
a :: t y la relación de destino de la forma t :: k diferentes. 5 :: Integer es verdadero en términos, pero no en tipos. "hi" :: Symbol es verdadero en tipos, pero no en términos. Esto requiere que la Demote tipos Demote vistas y tipos. - La biblioteca estándar usa
Int como una representación de índices de lista (y los singletons usan Nat en definiciones elevadas). Int y Nat son tipos no inductivos. A pesar de ser más eficientes que la codificación unaria de números naturales, no funcionan muy bien con definiciones inductivas como Fin o lookupS . Debido a esto, redefinimos la length como len . - Haskell no tiene mecanismos incorporados para elevar las funciones al nivel de tipos.
singletons codifica como familias de tipos privados y aplica la funcionalización para evitar la falta de uso parcial de las familias de tipos. Esta codificación es complicada. Además, tuvimos que poner la definición de len en una cita de Template Haskell para que los singletons generen su contraparte de nivel de tipo, Len . - No hay funciones dependientes incorporadas. Uno tiene que usar tipos de unidades para cerrar la brecha entre términos y tipos. En lugar de la lista habitual, pasamos
SList a lookupS . Por lo tanto, debemos tener en cuenta varias definiciones de listas a la vez. También conduce a gastos generales durante la ejecución del programa. Surgen debido a la conversión entre valores ordinarios y valores de tipos de unidades ( toSing , fromSing ) y debido a la transferencia del procedimiento de conversión (restricción SingKind ).
La inconveniencia es el problema menor. Peor aún, estas características del lenguaje no son confiables. Por ejemplo, informé el problema # 12564 en 2016, y también hay # 12088 del mismo año. Ambos problemas dificultan la implementación de programas más avanzados que los ejemplos de los libros de texto (como las listas de indexación). Estos errores de GHC todavía no están corregidos, y la razón, me parece, es que los desarrolladores simplemente no tienen suficiente tiempo. El número de personas que trabajan activamente en el GHC es sorprendentemente pequeño, por lo que algunas cosas no se mueven.
Resumen
Mencioné anteriormente que queremos las tres propiedades del código, así que aquí hay una tabla que ilustra el estado actual de las cosas:
Futuro brillante
De las tres opciones disponibles, cada una tiene sus inconvenientes. Sin embargo, podemos solucionarlos:
- Tome el estándar Haskell y agregue tipos dependientes directamente en lugar de una codificación incómoda mediante
singletons . (Es más fácil decirlo que hacerlo). - Tome Agda e implemente un generador de código eficiente y RTS para ello. (Es más fácil decirlo que hacerlo).
- Tome Haskell con extensiones, corrija errores y continúe agregando nuevas extensiones para simplificar la codificación de los tipos dependientes. (Es más fácil decirlo que hacerlo).
La buena noticia es que las tres opciones convergen en un punto (en cierto sentido). Imagine la extensión más pequeña del estándar Haskell que agrega tipos dependientes y, por lo tanto, le permite garantizar la exactitud del código por la forma en que está escrito. El código de Agda se puede compilar (transponer) a este idioma sin unsafeCoerce . Y Haskell con extensiones es, en cierto sentido, un prototipo inacabado de este lenguaje. Algo necesita ser mejorado, y algo necesita ser eliminado, pero al final, lograremos el resultado deseado.
Deshacerse de los singletons
Un buen indicador de progreso es la simplificación de la biblioteca de singletons . Como los tipos dependientes se implementan en Haskell, ya no se necesitan soluciones y manejo especial de casos especiales implementados en singletons . Finalmente, la necesidad de este paquete desaparecerá por completo. Por ejemplo, en 2016, usando la extensión -XTypeInType SingKind KProxy de SingKind y SomeSing . Este cambio fue posible gracias a la unión de tipos y tipos. Compare definiciones antiguas y nuevas:
class (kparam ~ 'KProxy) => SingKind (kparam :: KProxy k) where type DemoteRep kparam :: * fromSing :: SingKind (a :: k) -> DemoteRep kparam toSing :: DemoteRep kparam -> SomeSing kparam type Demote (a :: k) = DemoteRep ('KProxy :: KProxy k) data SomeSing (kproxy :: KProxy k) where SomeSing :: Sing (a :: k) -> SomeSing ('KProxy :: KProxy k)
En las definiciones anteriores, k aparece exclusivamente en las posiciones de vista, a la derecha de las anotaciones de la forma t :: k . Usamos kparam :: KProxy k para transferir k a los tipos.
class SingKind k where type DemoteRep k :: * fromSing :: SingKind (a :: k) -> DemoteRep k toSing :: DemoteRep k -> SomeSing k type Demote (a :: k) = DemoteRep k data SomeSing k where SomeSing :: Sing (a :: k) -> SomeSing k
En las nuevas definiciones, k mueve libremente entre las vistas y las posiciones de tipo, por lo que ya no necesitamos KProxy . La razón es que, comenzando con GHC 8.0, los tipos y tipos entran en la misma categoría sintáctica.
Hay tres mundos completamente separados en Haskell estándar: términos, tipos y vistas. Si mira el código fuente de GHC 7.10, puede ver un analizador separado para las vistas y una verificación por separado. GHC 8.0 ya no los tiene: el analizador y la validación de tipos y vistas son comunes.
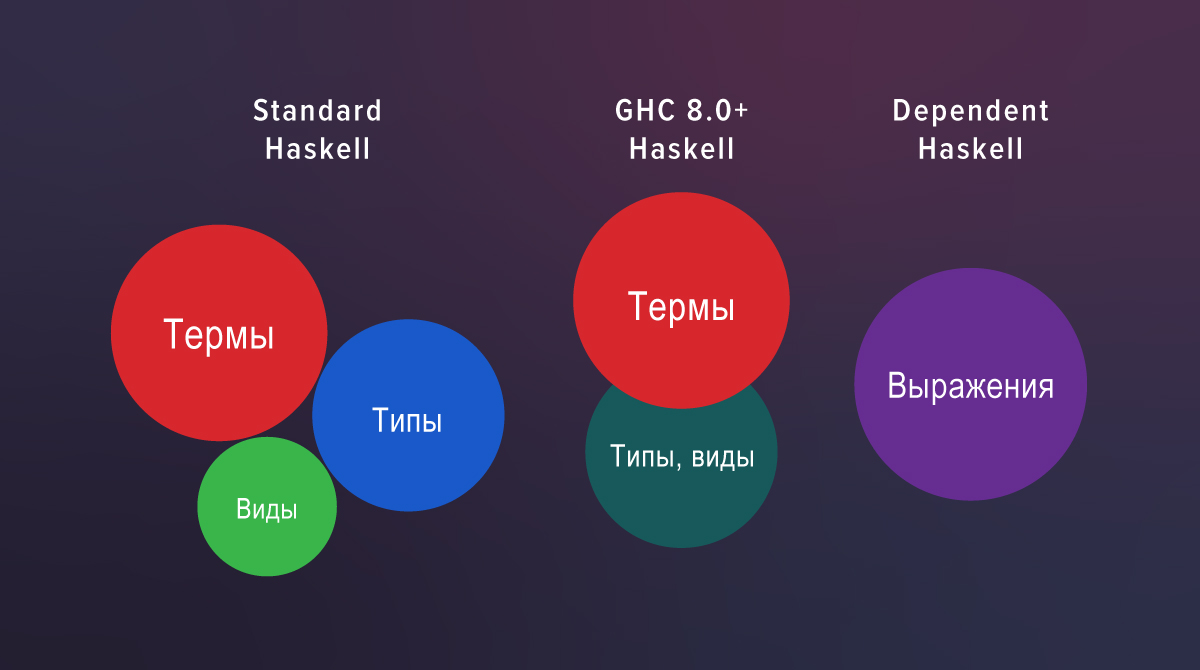
En Haskell con extensiones, la vista es solo el rol en el que se encuentra el tipo:
f :: T z -> ...
En GHC 8.0–8.4, todavía había algunas diferencias entre la resolución de nombres en tipos y tipos. Pero los minimicé a GHC 8.6: creé la extensión StarIsType e introduje la funcionalidad PolyKinds en PolyKinds . Hice las diferencias restantes como una advertencia para GHC 8.8, y las eliminé por completo en GHC 8.10 (la traducción de este párrafo se ha actualizado, en el original el trabajo realizado se describe como tareas futuras - nota del autor ).
¿Cuál es el siguiente paso? Echemos un vistazo a SingKind en la última versión de singletons :
class SingKind k where type Demote k = (r :: Type) | r -> k fromSing :: Sing (a :: k) -> Demote k toSing :: Demote k -> SomeSing k
La Demote tipo Demote necesaria para tener en cuenta las discrepancias entre la relación de escritura a :: t la relación de destino de la forma t :: k . Con mayor frecuencia (para tipos de datos algebraicos), Demote es un mapeo de identidad:
type Demote Bool = Booltype Demote [a] = [Demote a]type Demote (Either ab) = Either (Demote a) (Demote b)
Por lo tanto, Demote (Either [Bool] Bool) = Either [Bool] Bool . Esta observación nos lleva a hacer la siguiente simplificación:
class SingKind k where fromSing :: Sing (a :: k) -> k toSing :: k -> SomeSing k
Demote necesario Demote ! Y, de hecho, esto funcionaría tanto con Either [Bool] Bool como con otros tipos de datos algebraicos. En la práctica, sin embargo, estamos tratando con tipos de datos no algebraicos: Integer, Natural , Char , Text , etc. Si se usan como especies, no están pobladas: 1 :: Natural es cierto a nivel de términos, pero no a nivel de tipos. Debido a esto, estamos tratando con tales definiciones:
type Demote Nat = Natural type Demote Symbol = Text
La solución a este problema es criar tipos primitivos. Por ejemplo, el Text define así:
Si elevamos adecuadamente ByteArray# e Int# al nivel de tipos, podemos usar Text lugar de Symbol . Al hacer lo mismo con Natural y posiblemente un par de otros tipos, puede deshacerse de Demote , ¿verdad?
Por desgracia, no es así. En lo anterior, hice la vista gorda al tipo de datos más importante: funciones. También tienen una instancia especial de Demote :
type Demote (k1 ~> k2) = Demote k1 -> Demote k2 type a ~> b = TyFun ab -> Type data TyFun :: Type -> Type -> Type
~> este es un tipo con el que las funciones de nivel de tipo se codifican en singletons basadas en funcionalidades y familias de tipos privados.
Al principio, puede parecer una buena idea combinar ~> y -> , ya que ambos significan el tipo (tipo) de la función. El problema es que -> en la posición de tipo y -> en la posición de vista significan cosas diferentes. En el nivel de término, todas las funciones de a a b son de tipo a -> b . En el nivel de tipo, solo los constructores de a a b son de tipo a -> b , pero no son sinónimos de tipos ni familias de tipos. Para deducir los tipos, GHC supone que f ~ g a ~ b derivan de fa ~ gb , lo cual es cierto para los constructores, pero no para las funciones; es por eso que hay una restricción.
Por lo tanto, para elevar las funciones al nivel de tipos, pero para preservar la inferencia de tipos, tendremos que mover los constructores a un tipo separado. Lo llamamos a :-> b , porque realmente será cierto que f ~ g a ~ b siguen de fa ~ gb . Otras funciones seguirán siendo de tipo a -> b . Por ejemplo, Just :: a :-> Maybe a , pero al mismo tiempo isJust :: Maybe a -> Bool .
Cuando Demote , el último paso es deshacerse de Sing . Para hacer esto, necesitamos un nuevo cuantificador, un híbrido entre forall y -> . Echemos un vistazo más de cerca a la función isJust:
isJust :: forall a. Maybe a -> Bool isJust = \x -> case x of Nothing -> False Just _ -> True
La función isJust parametriza con el tipo a y luego con el valor x :: Maybe a . Estos dos parámetros tienen propiedades diferentes:
- Explicidad En la
isJust (Just "hello") , pasamos x = Just "hello" explícitamente, y a = String es generado implícitamente por el compilador. En Haskell moderno, también podemos forzar el paso explícito de ambos parámetros: isJust @String (Just "hello") . - Relevancia El valor pasado a la entrada a
isJust en el código se transmitirá durante la ejecución del programa: realizamos una comparación con la muestra usando case para verificar si es Nothing o Just . Por lo tanto, el valor se considera relevante. Pero su tipo se borra y no se puede comparar con el patrón: la función maneja Maybe Int , Maybe String , Maybe Bool , etc. Por lo tanto, se considera irrelevante. Esta propiedad también se llama parametricidad. - Adicción En
forall a. t forall a. t , el tipo t puede referirse a a , y por lo tanto, depender del particular pasado a . Por ejemplo, isJust @String es de tipo Maybe String -> Bool , y isJust @Int es de tipo Maybe Int -> Bool . Esto significa que forall es un cuantificador dependiente. Observe la diferencia con el parámetro de valor: no importa si llamamos isJust Nothing o isJust (Just …) , el tipo de resultado siempre es Bool . Por lo tanto, -> es un cuantificador independiente.
Para eliminar Sing , necesitamos un cuantificador explícito y relevante, como a -> b , y al mismo tiempo dependiente, como forall (a :: k). t forall (a :: k). t . Denotelo como foreach (a :: k) -> t . Para eliminar SingI , también presentamos un cuantificador dependiente relevante implícito, foreach (a :: k). t foreach (a :: k). t . Como resultado, los singletons no serán necesarios ya que acabamos de agregar funciones dependientes al lenguaje.
Una breve mirada a Haskell con tipos dependientes
Con el aumento de las funciones al nivel de tipos y el cuantificador foreach , podemos reescribir las lookupS siguiente manera:
data N = Z | SN len :: [a] -> N len [] = Z len (_:xs) = S (len xs) data Fin n where FZ :: Fin (S n) FS :: Fin n -> Fin (S n) lookupS :: foreach (xs :: [a]) -> Fin (len xs) -> a lookupS [] = \case{} lookupS (x:xs) = \case FZ -> x FS i' -> lookupS xs i'
En resumen, el código no lo hizo, sin embargo, es bastante bueno para ocultar código redundante. Sin embargo, el nuevo código es mucho más simple: ya no hay Demote , SingKind , SList , SNil , SCons , fromSing . No hay uso de TemplateHaskell , ya que ahora podemos llamar a la función len directamente en lugar de crear la familia de tipos Len . El rendimiento también será mejor, ya que ya no necesita convertir de fromSing .
Todavía tenemos que redefinir la length como len para devolver una N definida inductivamente en lugar de Int . Quizás este problema no debería considerarse en el marco de agregar tipos dependientes a Haskell, porque Agda también usa un N definido inductivamente en la función de lookup .
En algunos aspectos, Haskell con tipos dependientes es incluso más simple que Haskell estándar. Aún así, en términos, los tipos y los tipos se combinan en un solo lenguaje uniforme. Me puedo imaginar fácilmente escribir código en este estilo en un proyecto comercial para probar formalmente la corrección de los componentes clave de las aplicaciones. Muchas bibliotecas de Haskell pueden proporcionar interfaces más seguras sin la complejidad de los singletons .
Esto no será fácil de lograr. Nos enfrentamos a muchos problemas de ingeniería que afectan a todos los componentes del GHC: un analizador, resolución de nombres, verificación de tipos e incluso el lenguaje Core. Todo tendrá que ser modificado, o incluso completamente rediseñado.
Report generator