En la víspera del próximo lanzamiento del curso Algorithms for Developers, realizamos una lección abierta . Hablaron sobre la conocida idea de un árbol de segmentos, discutieron cómo construirlo, actualizarlo y rápidamente O(log n) calcular la suma de los números de cualquier segmento de un conjunto dado. El algoritmo es muy simple y económico: necesita memoria O(n) . Para consolidar el material, resolvieron el problema de la olimpiada.
El seminario web fue realizado por un programador y profesor experimentado, así como por el director del curso "Algoritmos para desarrolladores"
Evgeny Volosatov .
El dicho
Un árbol de segmentos es una estructura de datos que permite la búsqueda rápida algorítmicamente simple y logarítmica de la suma de los elementos de una matriz en un segmento dado.
Por ejemplo, imagine que necesita encontrar la suma de los siguientes números:

En este caso, necesitamos no solo calcular la suma de los números de la secuencia especificada (la suma de los elementos de una determinada matriz), sino lo
más rápido posible para encontrar la suma de cualquier secuencia de estos números . Es decir, podemos pedir algún intervalo (segmento) y dar la respuesta lo más rápido posible, cuál es la suma de los números de este intervalo:

¿Qué significa rápido? Esto significa
más rápido que si simplemente sumamos los números . Después de todo, puede haber millones y miles de millones de números ...
Fue el deseo de encontrar rápidamente la suma de elementos consecutivos lo que se convirtió en la motivación de nuestro seminario web. Además, estamos hablando no solo de la suma, sino también de otras tareas, por ejemplo, calcular cualquier función asociativa. Por lo tanto, estamos hablando de operaciones cuya ejecución no depende del orden de cálculo.
Volvamos a nuestra fila:

Obviamente, si queremos encontrar el resultado rápidamente, necesitamos calcular algunas cantidades por adelantado. Lo primero que viene a la mente es doblar en pares:

Ahora, si necesita encontrar la suma de números, podemos hacerlo casi al instante. Por ejemplo, para encontrar la suma del segmento mencionado anteriormente, será suficiente sumar 13 a 9. Todo es elemental: para encontrar la
suma de cuatro números, agregamos
solo dos .
Complicamos la tarea:
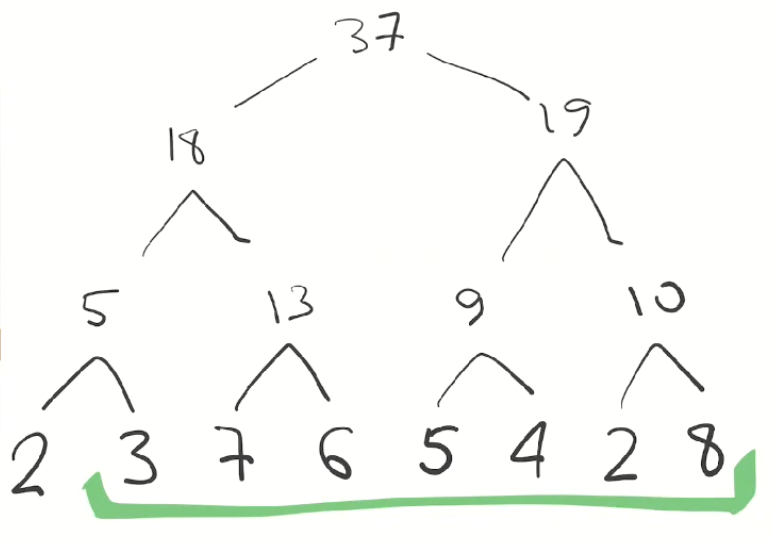
Para encontrar la suma de este segmento, necesitamos sumar los elementos que, de una forma u otra, cubren nuestro segmento:

Por supuesto, 3 + 13 + 19 = 35. Tenga en cuenta que para encontrar la
suma de los siete números , agregamos
solo tres . Si el segmento constara de mil elementos, sería suficiente agregar un promedio de 10 elementos, ya que tenemos una complejidad logarítmica con un logaritmo de base 2. ¡Y es rápido!
Árbol binario completo
Un árbol binario completo es un árbol, cada elemento del cual tiene exactamente dos hijos.
Para trabajar con un árbol binario completo, puede y debe usar una estructura de datos como una matriz.
Numerar esta matriz es conveniente desde uno . Numeramos cada elemento del árbol binario con números naturales del 1 al 2
n -1:

Toda la belleza del enfoque es que es muy fácil calcular el número de hijos y padres.
La fórmula para calcular el "niño izquierdo":
i * 2 , el "derecho":
i * 2 + 1 .

Por ejemplo, calculamos los números de niños en el quinto elemento:
- 5 x 2 = 10 ;
- 5 x 2 + 1 = 11 .
¿Y cómo pasar del "niño" al "padre"? Usamos
la división entera i / 2Ok, ¿y cómo determinar si el niño tiene izquierda o derecha? La respuesta es la siguiente: los
niños de la izquierda tienen números pares, los niños de la derecha tienen números impares .
Recuerda estos puntos.
Volviendo a nuestro ejemplo de un árbol binario, nos preguntamos, ¿cómo podemos construirlo? Mira, primero tenemos una serie de números:

Para ello necesitas construir un árbol binario. ¿Cuánta memoria se necesita para almacenar el árbol binario, en la parte inferior de los cuales se encuentran estos elementos?
La respuesta a esta pregunta es
2n si
n es una potencia de dos.
Vamos más allá, porque nos surgen dos preguntas más:
- ¿desde qué elemento necesita colocar los números de origen en una matriz de un árbol binario completo?
- ¿desde qué elemento y en qué dirección comenzaremos a llenar nuestro árbol con cantidades calculadas previamente?

La respuesta a la primera pregunta es bastante simple: tenemos 8 elementos, en total habrá 16 elementos en la matriz, lo que significa que el primer elemento estará numerado 16 - 8 = 8. Y comenzaremos a construir de izquierda a derecha y de abajo hacia arriba, comenzando desde el elemento 7, sumando valores en niños, así:

A continuación, debe determinar cómo encontrar la suma del segmento deseado. Volvemos a nuestro primer ejemplo, enumeramos los elementos y definimos un segmento, y denotamos el primer elemento en el segmento que se agregará con la letra L, y el último con R:

Ahora es necesario introducir un concepto más para que el algoritmo de acciones sea claro. Estamos hablando del concepto de elementos fundamentales y sus correspondientes segmentos fundamentales. El elemento fundamental es cualquier elemento del conjunto completo, y el segmento fundamental corresponde a él, es decir, aquellos elementos del conjunto inicial que son sus hijos / nietos inmediatos. Para el elemento fundamental con el número 4 "5", el segmento fundamental será del elemento 8 al 9: ["2"; "3"]:

En cuanto al elemento fundamental con el número 10 - "7" (lo designamos L), coincide con su segmento fundamental. ¿Es posible expandir este segmento fundamental sin ir más allá de LR? En nuestro caso, puedes. La regla para el borde izquierdo es la siguiente: si es un elemento secundario izquierdo, entonces el segmento fundamental puede expandirse, el nuevo elemento fundamental será el padre del actual. Es decir, podemos escribir lo siguiente en el programa:

Ahora pasemos al elemento derecho R. Es un elemento fundamental y un elemento secundario izquierdo, por lo que ya no podemos expandir el área (iremos más allá del segmento). Entonces, podemos agregar este elemento a la respuesta:

A continuación, necesita el elemento izquierdo para moverse hacia la derecha y el derecho hacia la izquierda. Para el elemento izquierdo con índice L = 10, el siguiente índice es 5, porque irá al padre. Pero irá primero a la derecha y luego hacia arriba:

Entonces, el valor de L se movió a un nivel superior y un poco a la derecha. ¿Cómo disminuirá R? Usando la fórmula (R - 1) / 2.

Aquí hay tal algoritmo. En cuanto a los siguientes valores de las variables L y R, se moverán de la siguiente manera:

Si no hay 8 elementos en el árbol, pero un número inconveniente, digamos 12, tendremos que agregar el árbol (el árbol binario debe estar completo) a 16.
La fórmula para calcular el número de elementos (se toma toda la parte del logaritmo):

Ahora calculamos la función asociativa de encontrar el
mínimo . Aquí está nuestro árbol y corte:

¿Cuántas veces crees que el elemento 5 estará involucrado en nuestra función, uno o dos? Por supuesto, uno, pero ¿cómo se verifica esto en el algoritmo? De hecho, este elemento es un hijo izquierdo o derecho, lo que significa que la acción se realizará para L o R.
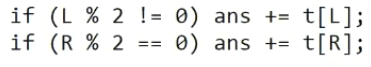
+
Ahora considere la operación de cambio. Digamos que algún elemento ha cambiado, por ejemplo, en lugar de 7, entró 0. Para que nuestro árbol de segmentos permanezca en condiciones de funcionamiento, necesitamos actualizar a todos los padres, y debemos ir a la cima.

Solución del problema olímpico
Uno de los requisitos para tales tareas es que todo debería funcionar rápidamente. Entonces, tenemos la siguiente condición:

Lo resolveremos utilizando el conocimiento sobre el árbol de segmentos. Como resultado, obtenemos el siguiente código C #:

Lo enviamos para su verificación, vemos que la
decisión se ha tomado y está completa , lo que significa que nuestro algoritmo funciona.

Eso es todo, si quieres más detalles,
mira el video completo . También puede leer
libremente los siguientes artículos del autor de nuestro maestro
Evgeny Volosatov sobre Habré:
-
Equilibrio de árboles rojo-negro - Tres casos ;
-
El caballo se mueve en pedazos. Tablero de ajedrez .