En toda la geografía: tareas de navegación y geodésicas en diferentes idiomas.

¡Saludos, queridos!

"... aunque se desconoce la verdadera posición del buque, pero no es accidental, lo es, pero se desconoce en qué punto" V. Aleksishin et al. Practical navigation, 2006. p. 71

"Los peatones salieron de los dos bordes de la galaxia ..." (C) Sergey Popov (Astrofísico)

A la luz de las nuevas tendencias en el estilo Art Nouveau, quería escribir sobre la resolución de problemas geodésicos en terreno plano. Pero hasta ahora, la afirmación de que la forma de la tierra se aproxima convenientemente por un elipsoide no es herejía y sedición, invito a todos los interesados ​​a unirse a modelos más conservadores.

• distancia entre dos puntos geográficos
• determinación de un punto por distancia conocida y ángulo acimutal
• determinación de la posición de un punto por distancias medidas a puntos conocidos (TOA, TOF)
• determinación de la posición de un punto por tiempos de llegada de señal medidos (TDOA)

Todo esto en C #, Rust y Matlab, en la esfera y elipsoides, con imágenes, gráficos, código fuente, debajo del corte.

Y esto, el KDPV relevante:



Para aquellos que tienen prisa (yo mismo lo estoy), aquí está el repositorio en GitHub , donde están todos los códigos fuente con pruebas y ejemplos.

El repositorio está organizado de manera muy simple: la biblioteca se presenta actualmente en tres idiomas y cada implementación está en su propia carpeta:

• C #
• Herrumbre
• Matlab

La implementación más completa en C #: a diferencia de las otras, existen los llamados métodos base larga virtual: esto es cuando un objeto cuya posición necesita determinar es estacionario, y hay distancias medidas desde diferentes puntos, con una posición conocida.

Para ver cómo funciona todo, con qué parámetros llama y qué regresa, y realizar el reconocimiento en la batalla, hay diferentes demostraciones y pruebas:

• Probar la aplicación de consola en C #
• Probar toda la biblioteca en Matlab
• Script de demostración TOA / TDOA con bellas imágenes en Matlab
• Script en Matlab para comparar la precisión de las soluciones a problemas geodésicos en una esfera (ecuaciones de Haversine) y en un elipsoide (ecuaciones de Vincenty)
• Para la implementación en Rust , el código de la biblioteca contiene pruebas. Y puede ver cómo funciona todo simplemente ejecutando el comando "Cargo-test"

Traté de hacer que la biblioteca fuera lo más independiente y autosuficiente posible. De modo que si lo desea, puede tomar la pieza deseada (refiriéndose a la fuente, por supuesto), sin arrastrar todo lo demás.

Casi siempre los ángulos están en radianes, distancias en metros, tiempo en segundos.

Ahora, comencemos desde el principio:

Tareas de topografía

Hay dos tareas geodésicas típicas: directa e inversa.

Si, por ejemplo, conozco mis coordenadas actuales (latitud y longitud), y luego caminé 1000 kilómetros estrictamente hacia el noreste, el pozo o el norte. ¿Qué coordenadas tendré ahora? - Para averiguar qué coordenadas tendré es resolver un problema geodésico directo.

Es decir: una tarea geodésica directa es encontrar las coordenadas de un punto por una distancia conocida y un ángulo de dirección.

Con el problema inverso, todo está completamente claro: por ejemplo, determiné mis coordenadas y luego caminé durante un tiempo en línea recta y nuevamente determiné mis coordenadas. Encontrar cuánto fui significa resolver el problema geodésico inverso.

Es decir: el problema geodésico inverso es encontrar la distancia entre dos puntos con coordenadas geográficas conocidas.

Puede resolver estos problemas de varias maneras, según la precisión necesaria y el tiempo que esté dispuesto a dedicarle.

La forma más fácil es imaginar que la tierra es plana : esta es una esfera. Probémoslo.
Aquí está la fórmula para resolver el problema directo ( fuente ):

$$

$$\ phi_2 = arcsin (sin \ phi_1cos \ delta + cos \ phi_1sin \ delta cos \ theta)$$

$$

$$\ lambda_2 = \ lambda_1 + atan2 (sin \ theta sin \ delta cos \ phi_1, cos \ delta-sin \ phi_1sin \ phi_2)$$

Aqui $$$\ phi_1$, $$$\ lambda_1$- latitud y longitud del punto de partida, $$$\ theta$- ángulo direccional, medido en sentido horario desde la dirección norte (cuando se ve desde arriba), $$$\ delta$- distancia angular d / R. d es la distancia medida (recorrida), y R es el radio de la tierra. $$$\ phi_2$, $$$\ lambda_2$- latitud y longitud del punto deseado (al que llegamos).

Para resolver el problema inverso, hay otra (fórmula no menos simple):

$$

$$a = sin ^ 2 (\ Delta \ phi / 2) + cos \ phi_1 cos \ phi_2 sin ^ 2 (\ Delta \ lambda / 2)$$

$$

$$d = R * atan2 (\ sqrt a, \ sqrt {1-a})$$

Donde $$$\ phi_1$, $$$\ lambda_1$y $$$\ phi_2$, $$$\ lambda_2$- coordenadas de puntos, R - radio de la tierra.

Las fórmulas descritas se llaman ecuaciones de Haversine.

• En una implementación de C #, las funciones correspondientes se llaman HaversineDirect y HaversineInverse y viven en Algorithms.cs .
• En una implementación de Rust, estas son las funciones haversine_direct y haversine_inverse .
• Finalmente, en Matlab, las funciones se almacenan en archivos separados, y aquí están ambas funciones:
  HaversineDirect y HaversineInverse

Para C #, proporcionaré los nombres de las funciones y un enlace al archivo donde se encuentran. Para Rust, solo los nombres de las funciones (ya que toda la biblioteca está en un archivo), y para Matlab, un enlace al archivo de script correspondiente, porque en Matlab hay una función: un script.

Obviamente, hay algún tipo de captura: la tierra no es una esfera, sino un plano, y esto de alguna manera debe afectar la aplicabilidad de estas fórmulas y / o la precisión de la solución.

Y de verdad. Pero para determinar esto, debe comparar con algo.
En 1975, Thaddeus Vincenty publicó una solución computacionalmente eficiente de problemas geodésicos directos e inversos en la superficie de un esferoide (mejor conocido como Elipsoide de la Revolución, camarada! Ellisoide de Rotación), que se ha vuelto casi estándar.

La descripción del dispositivo del método se basa en un artículo separado, por lo que me limitaré a enviar el trabajo original de Vincenti y una calculadora en línea con una descripción del algoritmo.

En la biblioteca UCNLNav, la solución de problemas geodésicos directos e inversos utilizando las fórmulas de Vincenti reside en las siguientes funciones:

• C #: VincentyDirect y VincentyInverse en Algorithms.cs .
• Óxido: vincenty_inverse y vincenty_direct
• Matlab: Nav_vincenty_direct y Nav_vincenty_inverse .

Porque La solución de Vincenti es iterativa, entonces el número máximo de iteraciones (it_limit) está presente en la lista de parámetros, y el número real de iteraciones está en la lista de resultados. También hay un umbral que especifica una condición de detención (epsilon). En la mayoría de los casos, no se requieren más de 10 iteraciones, pero para puntos casi antipodales (como los polos norte y sur), el método converge mal y pueden requerirse hasta 2000 iteraciones.

La diferencia más importante es que estas fórmulas ejecutan la solución en un esferoide, y sus parámetros deben transferirse a las funciones. Hay una estructura simple para esto que lo describe.

En todas las implementaciones, uno de los elipsoides estándar se puede obtener en una línea. (Muy a menudo, se utiliza WGS84 [https://en.wikipedia.org/wiki/World_Geodetic_System] y lo daremos como ejemplo):

• En C #: Algorithms.cs tiene un campo estático Algorithms.WGS84Ellipsoid: se puede pasar a los métodos.
• En óxido:

  let el: Ellipsoid = Ellipsoid::from_descriptor(&WGS84_ELLIPSOID_DESCRIPTOR); 

• En Matlab:

   el = Nav_build_standard_ellipsoid('WGS84'); 

El nombre de los parámetros restantes es bastante obvio y no debe causar ambigüedades.

Para comprender cuánto nos costará usar soluciones para una esfera en lugar de una elipse, hay un script en la implementación de Matlab.

En Matlab, es increíblemente conveniente mostrar cualquier cosa sin gestos innecesarios, así que lo elegí para la demostración.

La lógica de su guión:

1. Tomamos un punto con coordenadas arbitrarias

 sp_lat_rad = degtorad(48.527683); sp_lon_rad = degtorad(44.558815); 

y una dirección arbitraria (elegí sobre el oeste):

 fwd_az_rad = 1.5 * pi + (rand * pi / 4 - pi / 8); 

2. Pasamos de él a una distancia cada vez mayor. ¿Por qué establecemos de inmediato el número de pasos y el tamaño del paso?

 n_samples = 10000; step_m = 1000; % meters distances = (1:n_samples) .* step_m; 

3. Para cada paso, resolvemos el problema geodésico directo en la esfera y en el elipsoide, obteniendo el punto deseado:

 [ h_lats_rad(idx), h_lons_rad(idx) ] = Nav_haversine_direct(sp_lat_rad,... sp_lon_rad,... distances(idx),... fwd_az_rad,... el.mjsa_m); [ v_lats_rad(idx), v_lons_rad(idx), v_rev_az_rad, v_its ] = Nav_vincenty_direct(sp_lat_rad,... sp_lon_rad,... fwd_az_rad,... distances(idx),... el,... VNC_DEF_EPSILON, VNC_DEF_IT_LIMIT); 

4. Para cada paso, resolvemos problemas geodésicos inversos: calculamos las distancias entre los resultados obtenidos en una esfera y un elipsoide:

 [ v_dist(idx) a_az_rad, a_raz_rad, its, is_ok ] = Nav_vincenty_inverse(h_lats_rad(idx),... h_lons_rad(idx),... v_lats_rad(idx),... v_lons_rad(idx),... el,... VNC_DEF_EPSILON, VNC_DEF_IT_LIMIT); 

5. Verificamos soluciones directas inversas para ambos métodos:

 [ ip_v_dist(idx) a_az_rad, a_raz_rad, its, is_ok ] = Nav_vincenty_inverse(sp_lat_rad,... sp_lon_rad,... v_lats_rad(idx),... v_lons_rad(idx),... el,... VNC_DEF_EPSILON, VNC_DEF_IT_LIMIT); ip_h_dist(idx) = Nav_haversine_inverse(sp_lat_rad,... sp_lon_rad,... v_lats_rad(idx),... v_lons_rad(idx),... el.mjsa_m); 

En el guión, esta secuencia se realiza primero para un paso = 1000 m, y luego para un paso = 1 metro.

Primero, veamos cómo los resultados de las decisiones directas difieren en las coordenadas (latitud y longitud), para lo cual calculamos los vectores "delta", ya que todo está escrito en Matlab en una línea:

 d_lat_deg = radtodeg(v_lats_rad - h_lats_rad); %    ( ) d_lon_deg = radtodeg(v_lons_rad - h_lons_rad); %    ( ) 

La abscisa se mostrará en una escala logarítmica, como nuestras distancias varían de 1 a 10,000 km:

 figure semilogx(distances, d_lat_deg, 'r'); title('Direct geodetic problem: Vincenty vs. Haversine (Latitude difference)'); xlabel('Distance, m'); ylabel('Difference, °'); figure semilogx(distances, d_lon_deg, 'r'); title('Direct geodetic problem: Vincenty vs. Haversine (Longitude difference)'); xlabel('Distance, m'); ylabel('Difference, °'); 

Como resultado, obtenemos tales gráficos para la latitud:



Y por longitud:



No entiendo en grados, siempre me guía el método para estimar "a ojo":
1 ° de algo es un promedio de 100-110 km. Y si el error es más de una millonésima parte o al menos una centésima parte de un grado, esta es una mala noticia.

A continuación, observamos las distancias entre el punto de partida y el punto obtenido en cada paso de acuerdo con las fórmulas para la esfera y el elipsoide. Calculamos la distancia utilizando las fórmulas de Vincenti (ya que obviamente es más preciso: el autor promete un error en milímetros). Los gráficos en metros y kilómetros son mucho más tangibles y familiares:

 figure semilogx(distances, v_dist, 'r'); title('Direct geodetic problem: Vincenty vs. Haversine (Endpoint difference by Vincenty)'); xlabel('Distance, m'); ylabel('Difference, m'); 

Como resultado, obtenemos la siguiente imagen:



Resulta que en rangos de 10,000 km los métodos divergen en 10 km.

Si ahora todo se repite para un paso 1000 veces más pequeño, es decir cuando el rango completo a lo largo del eje X no es de 10,000 km sino solo de 10 km, la imagen es la siguiente:



Es decir, a una distancia de 10 km solo corren 20 metros, y durante 1-2 metros las fórmulas divergen solo a distancias de aproximadamente 1000 metros.

La conclusión del capitán es obvia: si la precisión de las fórmulas con la solución en la esfera es suficiente para el problema, entonces las usamos, son más simples y más rápidas.

Bueno, para aquellos para quienes la precisión milimétrica no es suficiente, en 2013 se publicó un trabajo que describe la solución de problemas geodésicos con precisión nanométrica (!). No estoy seguro de que pueda encontrar de inmediato dónde podría ser necesario, excepto para los estudios geodésicos al construir detectores de ondas gravitacionales o algo completamente fantástico).

Ahora pasemos al más sabroso:

Resolviendo problemas de navegación

Por el momento, la biblioteca puede determinar:

• La ubicación del objeto por distancia a puntos, con coordenadas conocidas en 2D y 3D. Esto es lo que llamamos TOA - Hora de llegada (o más correctamente, TOF - Hora de vuelo)
• La ubicación del objeto por las diferencias en los tiempos de llegada en 2D y 3D. Esto es lo que llamamos TDOA (Diferencia horaria de llegada).

En realidad, siempre medimos los rangos o tiempos de llegada de una señal (y, en consecuencia, su diferencia) con errores, con ruido. Por lo tanto, la solución de los problemas de navegación en la gran mayoría de los casos es la minimización de errores. Método de mínimos cuadrados y eso es todo .

Lo que debe minimizarse se llama función residual.

Para las tareas TOA, se ve así:

$$

$$argmin \ epsilon (x, y, z) = \ sum_ {i = 1} ^ {N} [\ sqrt {(x-x_i) ^ 2 + (y-y_i) ^ 2 + (z-z_i) ^ 2 )} - r_i] ^ 2$$

Donde $$$\ epsilon (x, y, z)$- el valor de la función residual para un determinado punto con coordenadas $$$(x, y, z)$; N es el número de puntos de control que tienen coordenadas $$$(x_i, y_i, z_i)$, $$$r_i$- distancias medidas desde los puntos de referencia hasta el objeto posicionado.

Y para tareas de TDOA como esta:

$$

$$argmin \ epsilon (x, y, z) = \ sum_ {i = 1, j = 2, i \ neq j} ^ {N} [\ sqrt {(x-x_i) ^ 2 + (y-y_i) ^ 2+ (z-z_i) ^ 2)} - \\ \ sqrt {(x-x_j) ^ 2 + (y-y_j) ^ 2 + (z-z_j) ^ 2)} - \ nu (t_ {Ai} -t_ {Aj})] ^ 2$$

Aquí todo es igual, solo se consideran diferentes pares de puntos de referencia y los tiempos de llegada correspondientes $$$t_ {Ai}$y $$$t_ {Aj}$y $$$\ nu$- velocidad de propagación de la señal.

Y así, estas funciones se ven en el código:




Como puede ver, ambas funciones funcionan con un número variable de puntos o líneas de control. En general, las tareas pueden ser diferentes y las funciones residuales también.

Por ejemplo, puede resolver el problema no solo de determinar la ubicación, sino también de determinar la orientación. En este caso, la función residual contendrá uno o más ángulos.

Consideremos con más detalle la estructura interna de la biblioteca.

En esta etapa, la biblioteca trabaja con tareas 2D y 3D y el solucionador mismo no sabe y no quiere saber cómo se ve la funcionalidad minimizada. Esto se logra de la siguiente manera.

El solucionador tiene dos aspectos: solucionadores 2D y 3D basados ​​en el método Nelder-Mead o, como también se le llama, el método Simplex.

Dado que este método no requiere el cálculo de derivadas (la llamada minimización libre de derivadas ), idealmente, el usuario de la biblioteca puede usar sus propias funciones residuales si es necesario. Además, teóricamente no hay un límite superior en el número de puntos de control utilizados para resolver el problema.

En C # y Rust, los solucionadores 2D y 3D son métodos genéricos:

 public static void NLM2D_Solve<T>(Func<T[], double, double, double, double> eps, T[] baseElements,... //       : fxi[0] = eps(baseElements, xix[0], xiy[0], z); 

Un ejemplo de llamar al solucionador mismo:

 public static void TOA_NLM2D_Solve(TOABasePoint[] basePoints, double xPrev, double yPrev, double z, int maxIterations, double precisionThreshold, double simplexSize, out double xBest, out double yBest, out double radialError, out int itCnt) { NLM2D_Solve<TOABasePoint>(Eps_TOA3D, basePoints, xPrev, yPrev, z, maxIterations, precisionThreshold, simplexSize, out xBest, out yBest, out radialError, out itCnt); } 

Sobre el óxido ...

 pub fn nlm_2d_solve<T>(eps: Eps3dFunc<T>, base_elements: &Vec<T>... 

Todo es idéntico, exacto a la sintaxis del lenguaje.

En Matlabe, con su voluntarismo inherente, el solucionador mismo no tiene idea de cuáles son los elementos básicos que se le pasan: el usuario mismo debe asegurarse de que el enlace a la función residual y el conjunto de elementos de soporte pasados ​​al solucionador sean compatibles:

 function [ x_best, y_best, rerr, it_cnt ] = Nav_nlm_2d_solve(eps, base_elements, .... 

Y en consecuencia, la llamada al solucionador se ve así:

 function [ x_best, y_best, rerr, it_cnt ] = Nav_toa_nlm_2d_solve(base_points, x_prev, y_prev, z,... max_iterations, precision_threshold, simplex_size) [ x_best, y_best, rerr, it_cnt ] = Nav_nlm_2d_solve(@Nav_eps_toa3d, base_points, x_prev, y_prev, z,... max_iterations, precision_threshold, simplex_size); end 

Hay un script especial de Matlab para demostrar la solución de los problemas TOA y TDOA.

La demostración en 2D no fue elegida por casualidad: no estoy seguro de poder descubrir cómo mostrar la función residual tridimensional de manera simple e informativa =)

Entonces Al comienzo del script hay parámetros que se pueden cambiar:

 %% parameters n_base_points = 4; %    area_width_m = 1000; %   max_depth_m = 100; %   ( Z) propagation_velocity = 1500;%     -  max_iterations = 2000; %    precision_threshold = 1E-9; %   simplex_size = 1; %      contour_levels = 32; %      range_measurements_error = 0.01; % 0.01 means 1% of corresponding slant range %    -   1% 

La posición del punto deseado se establece aleatoriamente en el área especificada:

 %% actual target location r_ = rand * area_width_m / 2; az_ = rand * 2 * pi; actual_target_x = r_ * cos(az_); actual_target_y = r_ * sin(az_); actual_target_z = rand * max_depth_m; 

A continuación, coloque aleatoriamente los puntos de control, calcule la distancia desde el deseado hasta ellos y muestre todo:

 %% base points figure hold on grid on base_points = zeros(n_base_points, 4); for n = 1:n_base_points r_ = area_width_m / 2 - rand * area_width_m / 4; az_ = (n - 1) * 2 * pi / n_base_points; base_x = r_ * cos(az_); base_y = r_ * sin(az_); base_z = rand * max_depth_m; dist_to_target = Nav_dist_3d(base_x, base_y, base_z, actual_target_x, actual_target_y, actual_target_z); base_points(n, :) = [ base_x base_y base_z dist_to_target ]; end N =1:n_base_points; plot3(actual_target_x, actual_target_y, actual_target_z,... 'p',... 'MarkerFaceColor', 'red',... 'MarkerEdgeColor', 'blue',... 'MarkerSize', 15); plot3(base_points(N, 1), base_points(N, 2), base_points(N, 3),... 'o',... 'MarkerFaceColor', 'green',... 'MarkerEdgeColor', 'blue',... 'MarkerSize', 15); for n = 1:n_base_points line([ actual_target_x, base_points(n, 1) ], [ actual_target_y, base_points(n, 2) ], [ actual_target_z, base_points(n, 3) ]); end view(45, 15); legend('target', 'base points'); title('Placement of base stations and the target'); xlabel('X coordinate, m'); ylabel('Y coordinate, m'); zlabel('Z coordinate, m'); 

Como resultado, obtenemos la siguiente imagen:



Agregue errores aleatorios a las mediciones de distancia:

 % adding range measurement errors base_points(N, 4) = base_points(N, 4) + base_points(N, 4) *... (rand * range_measurements_error - range_measurements_error / 2); 

Construimos la función residual para la región seleccionada con una cierta destrucción; de lo contrario, los cálculos pueden llevar un tiempo notable. Elegí el tamaño del área de 1000 x 1000 metros y considero la función residual en toda el área después de 10 metros:

 % error surface tiles tile_size_m = 10; n_tiles = area_width_m / tile_size_m; %% TOA solution error_surface_toa = zeros(n_tiles, n_tiles); for t_x = 1:n_tiles for t_y = 1:n_tiles error_surface_toa(t_x, t_y) = Nav_eps_toa3d(base_points,... t_x * tile_size_m - area_width_m / 2,... t_y * tile_size_m - area_width_m / 2,... actual_target_z); end end figure surf_a = [1:n_tiles] * tile_size_m - area_width_m / 2; surf(surf_a, surf_a, error_surface_toa); title('TOA solution: Residual function'); xlabel('X coordinate, m'); ylabel('Y coordinate, m'); view(45, 15); 

Aquí está la función residual:



Por supuesto, era un poco astuto: las posiciones relativas de los puntos de control y la deseada se eligen para que siempre formen una figura convexa con el punto deseado dentro. En gran parte debido a esto, la superficie tiene un mínimo, que es sin ningún problema.

Un lector arrogante puede cambiar este orden de cosas y tratar de establecer los puntos de anclaje y el deseado por accidente.

Ahora muéstrelo todo junto. Esto es difícil de hacer en la superficie: diferentes valores a lo largo del eje vertical. Por lo tanto, es conveniente dibujar todo en un corte bidimensional:

 figure hold on contourf(surf_a, surf_a, error_surface_toa, contour_levels); plot(actual_target_x, actual_target_y,... 'p',... 'MarkerFaceColor', 'red',... 'MarkerEdgeColor', 'blue',... 'MarkerSize', 15); plot(base_points(N, 1), base_points(N, 2),... 'o',... 'MarkerFaceColor', 'green',... 'MarkerEdgeColor', 'blue',... 'MarkerSize', 15); [ x_prev, y_prev ] = Nav_toa_circles_1d_solve(base_points, actual_target_z, pi / 180, 10, 0.1); [ x_best, y_best, rerr, it_cnt ] = Nav_toa_nlm_2d_solve(base_points, x_prev, y_prev, actual_target_z,... max_iterations, precision_threshold, simplex_size); plot(x_best, y_best,... 'd',... 'MarkerFaceColor', 'yellow',... 'MarkerEdgeColor', 'blue',... 'MarkerSize', 7); title(sprintf('TOA Solution: Residual function. Target location estimated with E_{radial} = %.3f m in %d iterations', rerr, it_cnt)); xlabel('X coordinate, m'); ylabel('Y coordinate, m'); legend('Residual function value', 'Actual target location', 'Base points', 'Estimated target location'); 

El resultado es algo como esto:



El error radial se muestra en el encabezado del gráfico, la raíz del valor final de la función residual. El gráfico muestra que la ubicación real y la calculada están en buen acuerdo, pero la escala no nos permite determinar qué tan bien.

Por lo tanto, mostramos la ubicación calculada del punto deseado y su ubicación real por separado y calculamos la distancia entre ellos:

 figure hold on grid on dx = actual_target_x - x_best; dy = actual_target_y - y_best; plot(0, 0,... 'p',... 'MarkerFaceColor', 'red',... 'MarkerEdgeColor', 'blue',... 'MarkerSize', 15); plot(dx, dy,... 'd',... 'MarkerFaceColor', 'yellow',... 'MarkerEdgeColor', 'blue',... 'MarkerSize', 7); plot(-dx * 2, -dy * 2, '.w'); plot(dx * 2, dy * 2, '.w'); d_delta = Nav_dist_3d(actual_target_x, actual_target_y, actual_target_z, x_best, y_best, actual_target_z); title(sprintf('TOA Solution: Actual vs. Estimated location, distance: %.3f m', d_delta)); xlabel('X coordinate, m'); ylabel('Y coordinate, m'); legend('Actual target location', 'Estimated target location'); 

Así es como se ve:



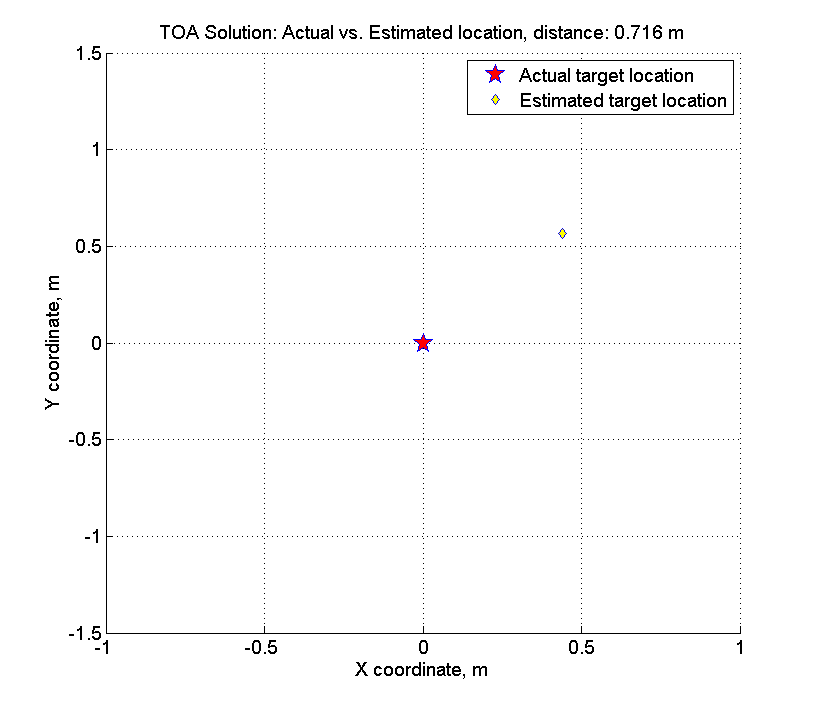
Recuerde que tenemos la amplitud de un error aleatorio: 1% del rango, en promedio, el rango es de ~ 200-400 metros, es decir La amplitud del error es de unos 2-4 metros. Al buscar una solución, cometimos un error de solo 70 centímetros.

Ahora, por analogía, intentaremos resolver el problema de TDOA con los mismos datos. Para hacer esto, pretendemos que solo conocemos los tiempos de llegada de las señales desde el punto deseado a los puntos de referencia (o viceversa, no importa), simplemente dividimos nuestras distancias por la velocidad de propagación de la señal, solo sus diferencias y no los valores absolutos son importantes.

 % since TDOA works with time difference of arriaval, % we must recalculate base point's distances to times base_points(N,4) = base_points(N,4) / propagation_velocity; base_lines = Nav_build_base_lines(base_points, propagation_velocity); 

Construye y dibuja una superficie de errores:

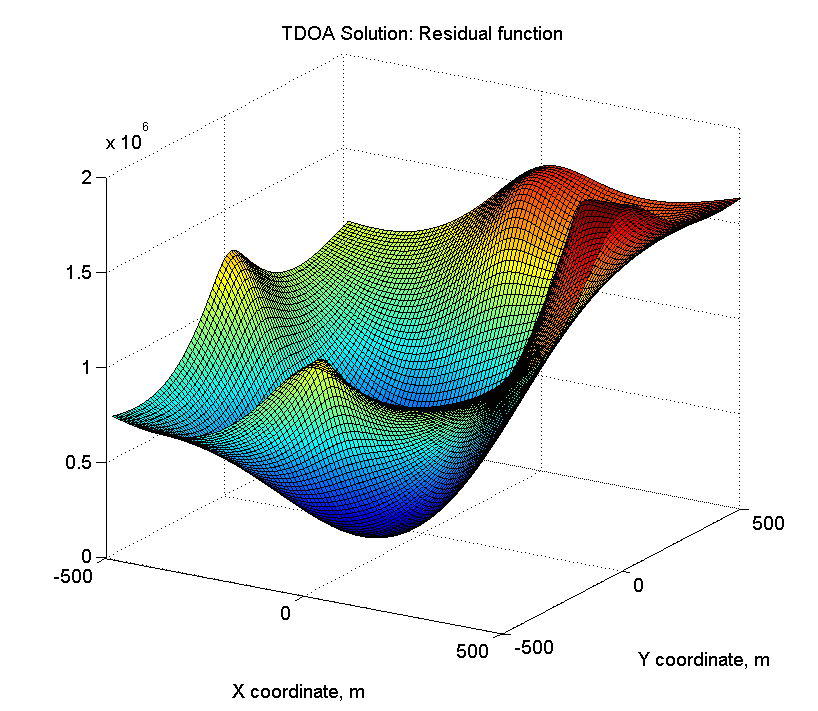
 error_surface_tdoa = zeros(n_tiles, n_tiles); for t_x = 1:n_tiles for t_y = 1:n_tiles error_surface_tdoa(t_x, t_y) = Nav_eps_tdoa3d(base_lines,... t_x * tile_size_m - area_width_m / 2,... t_y * tile_size_m - area_width_m / 2,... actual_target_z); end end figure surf(surf_a, surf_a, error_surface_tdoa); title('TDOA Solution: Residual function'); xlabel('X coordinate, m'); ylabel('Y coordinate, m'); view(45, 15); 

Resulta algo como esto:



Y la vista desde arriba con puntos de referencia, las posiciones reales y calculadas del punto deseado:



Y con más detalle, la discrepancia entre la ubicación real y la calculada:



En este caso particular, la solución TDOA resultó ser incluso mejor que la solución TOA: el error absoluto es de 0,3 metros.

Bueno en el modelo: siempre sabe exactamente dónde se encuentra realmente el punto deseado. Es peor en el aire, tal vez hay varios puntos de vista, bajo el agua que acabas de calcular algo y eso es todo, en el 99% de los casos, para calcular la desviación de la ubicación real, también debe calcularse primero (esta ubicación).

Ahora, como conclusión, combinaremos nuestro nuevo conocimiento sobre tareas geodésicas y de navegación.

Acorde final

Lo más cerca posible de la situación en la vida real:

• Supongamos que nuestros puntos de referencia tienen receptores GNSS incorporados y que solo conocemos sus coordenadas geográficas
• la coordenada vertical es desconocida para nosotros (problema 3D)
• medimos solo los tiempos de llegada de la señal desde los puntos de referencia en el deseado o viceversa

Esta situación se describe en la prueba más reciente en las tres implementaciones. Privado de alguna manera a Rust, y analizaré el ejemplo final sobre él.

Entonces, la prueba más reciente en la biblioteca. Como coordenadas del punto deseado, elegí un lugar en el parque, donde a menudo camino con el perro.

 #[test] fn test_tdoa_locate_3d() { let el: Ellipsoid = Ellipsoid::from_descriptor(&WGS84_ELLIPSOID_DESCRIPTOR); let base_number = 4; // 4   let start_base_z_m: f64 = 1.5; //  Z     let base_z_step_m = 5.0; //        5  let actual_target_lat_deg: f64 = 48.513724 // singed degrees let actual_target_lon_deg: f64 = 44.553248; // signed degrees let actual_target_z_m: f64 = 25.0; // meters - ,    ! // generate base points via Vincenty equations let mut base_points = Vec::new(); let start_dst_projection_m = 500.0; //      500  let dst_inc_step_m = 50.0; //   -  50   // azimuth step let azimuth_step_rad = PI2 / base_number as f64; //     let actual_target_lat_rad = actual_target_lat_deg.to_radians(); let actual_target_lon_rad = actual_target_lon_deg.to_radians(); // signal propagation speed let velocity_mps = 1450.0; // m/s,        //     for base_idx in 0..base_number { //        let dst_projection_m = start_dst_projection_m + dst_inc_step_m * base_idx as f64; //       let azimuth_rad = azimuth_step_rad * base_idx as f64; //        Vincenty let vd_result = vincenty_direct(actual_target_lat_rad, actual_target_lon_rad, azimuth_rad, dst_projection_m, &el, VNC_DEF_EPSILON, VNC_DEF_IT_LIMIT); //   Z let base_z_m = start_base_z_m + base_z_step_m * base_idx as f64; //        let dz_m = actual_target_z_m - base_z_m; //      let slant_range_m = (dst_projection_m * dst_projection_m + dz_m * dz_m).sqrt(); //   .          Rust   ! base_points.push((vd_result.0.to_degrees(), vd_result.1.to_degrees(), base_z_m, slant_range_m / velocity_mps)); } //     -   NAN- let lat_prev_deg = f64::NAN; let lon_prev_deg = f64::NAN; let prev_z_m = f64::NAN; //   let tdoa_3d_result = tdoa_locate_3d(&base_points, lat_prev_deg, lon_prev_deg, prev_z_m, NLM_DEF_IT_LIMIT, NLM_DEF_PREC_THRLD, 10.0, &el, velocity_mps); //          let vi_result = vincenty_inverse(actual_target_lat_rad, actual_target_lon_rad, tdoa_3d_result.0.to_radians(), tdoa_3d_result.1.to_radians(), &el, VNC_DEF_EPSILON, VNC_DEF_IT_LIMIT); assert!(vi_result.0 < start_dst_projection_m * 0.01, "Estimated location is farer than limit (1%): {}", vi_result.0); assert_approx_eq!(tdoa_3d_result.2, actual_target_z_m, start_dst_projection_m * 0.05); assert!(tdoa_3d_result.3 < start_dst_projection_m * 0.01, "Residual function greater than limit (1%): {}", tdoa_3d_result.3); assert!(tdoa_3d_result.4 < NLM_DEF_IT_LIMIT, "Method did not converge: iterations limit exeeded {}", tdoa_3d_result.4); } 

Como resultado, tenemos:
Ubicación real (Lat, Lon, Z): 48.513724 44.553248 25
Posición calculada (Lat, Lon, Z): 48.513726 44.553252 45.6
Distancia entre puntos en la superficie (m): 0.389
Diferencia en la coordenada Z (m): 20,6

La coincidencia de "plan" es muy buena, el error es de solo 40 centímetros y la coordenada vertical es de 20 metros. ¿Por qué sucede esto? Sugiero a los lectores que piensen =)

PS

La biblioteca descrita es un proyecto puramente educativo, que planeo desarrollar y reponer aún más. Los planes incluyen la implementación en C y la redacción de documentación completa.

En esto, déjenme despedirme, gracias por su atención.Estaré infinitamente contento con cualquier comentario.
Espero que el artículo y la biblioteca sean útiles.
Informe cualquier error (gramatical y lógico): lo corregiré.

PPS

Por si acaso, aquí hay un enlace a los intérpretes en línea (y no solo) de Matlab / Octave, que utilizo yo mismo:

• Compilador en línea de octavas
• Octave en línea
• Octava GNU