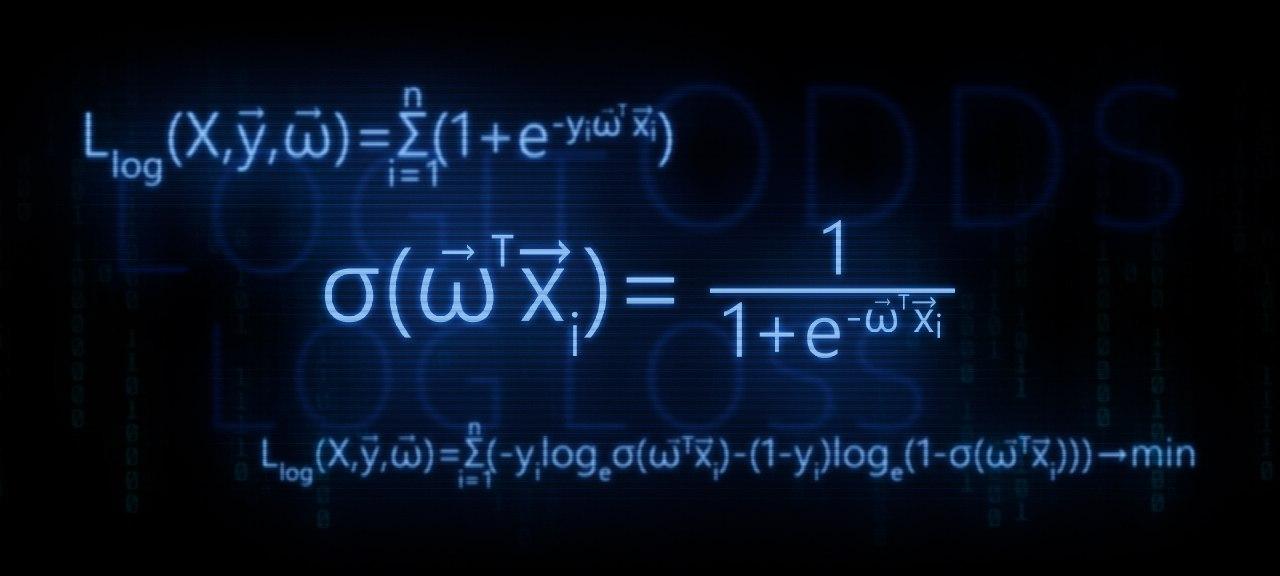
En este artículo, analizaremos los cálculos teóricos de convertir
la función de regresión lineal a la función de transformación de registro inverso (en otras palabras, la función de respuesta logística) . Luego, utilizando el arsenal del
método de máxima verosimilitud , de acuerdo con el modelo de regresión logística, derivamos la función de pérdida
Pérdida logística , o en otras palabras, determinamos la función por la cual se seleccionan los parámetros del vector de peso en el modelo de regresión logística
v e c w .
El bosquejo del artículo:
- Vamos a repetir sobre la relación directa entre dos variables.
- Identificamos la necesidad de convertir la función de regresión lineal f ( w , x i ) = v e c w T v e c x i a la función de respuesta logística s i g m a ( v e c w T v e c x i ) = f r a c 1 1 + e - v e c w T v e c x i
- Llevamos a cabo las transformaciones y derivamos la función de respuesta logística.
- Tratemos de entender por qué el método de mínimos cuadrados es malo al elegir parámetros v e c w Características de pérdida logística
- Usamos el método de máxima verosimilitud para determinar la función de selección de parámetros v e c w :
5.1. Caso 1: Función de pérdida logística para objetos con designación de clase 0 y 1 :
Llog(X, vecy, vecw)= sum limitsni=1(−yi mkern2muloge mkern5mu sigma( vecwT vecxi)−(1−yi) mkern2muloge mkern5mu(1− sigma( vecwT vecxi))) rightarrowmin
5.2. Caso 2: Función de pérdida logística para objetos con designaciones de clase -1 y +1 :
Llog(X, vecy, vecw)= sum limitsni=1 mkern2muloge mkern5mu(1+e−yi vecwT vecxi) rightarrowmin
El artículo está repleto de ejemplos simples en los que todos los cálculos son fáciles de hacer verbalmente o en papel, en algunos casos se puede requerir una calculadora. Así que prepárate :)
Este artículo está más dirigido a especialistas en datos con un nivel inicial de conocimiento en los conceptos básicos del aprendizaje automático.
El artículo también proporcionará código para dibujar gráficos y cálculos. Todo el código está escrito en
python 2.7 . Explicaré de antemano la "novedad" de la versión utilizada: esta es una de las condiciones para tomar un curso bien conocido de
Yandex en la plataforma en línea no menos conocida para la educación en línea
Coursera , y, como puede suponer, el material se preparó en base a este curso.
01. línea recta
Es bastante razonable hacer la pregunta: ¿dónde está la relación directa y la regresión logística?
¡Todo es simple! La regresión logística es uno de los modelos que pertenecen al clasificador lineal. En palabras simples, el objetivo de un clasificador lineal es predecir valores objetivo
y de variables (regresores)
X . Se cree que la relación entre los signos
X y valores objetivo
y lineal Por lo tanto, el nombre del clasificador en sí es lineal. Generalizado en términos generales, el modelo de regresión logística se basa en el supuesto de que existe una relación lineal entre las características.
X y valores objetivo
y . Aquí está, una conexión.
El estudio es el primer ejemplo, y con razón, sobre la dependencia directa de las cantidades estudiadas. En el proceso de preparación del artículo, me encontré con un ejemplo que ya tiene
dolor de garganta : la dependencia de la intensidad actual del voltaje
("Análisis de regresión aplicada", N. Draper, G. Smith) . Aquí lo consideraremos también.
De acuerdo con la
ley de Ohm:I=U/R donde
I - fuerza actual
U - voltaje
R - resistencia.
Si no supiéramos la
ley de Ohm , podríamos encontrar la dependencia empíricamente cambiando
U y midiendo
I mientras apoya
R arreglado Entonces veríamos que el gráfico de dependencia
I de
U da una línea más o menos recta que pasa por el origen. Dijimos "más o menos", porque, aunque la dependencia es realmente precisa, nuestras mediciones pueden contener pequeños errores y, por lo tanto, los puntos en el gráfico pueden no caer exactamente en la línea, pero se dispersarán aleatoriamente a su alrededor.
Gráfico 1 "Dependencia
I de
U "
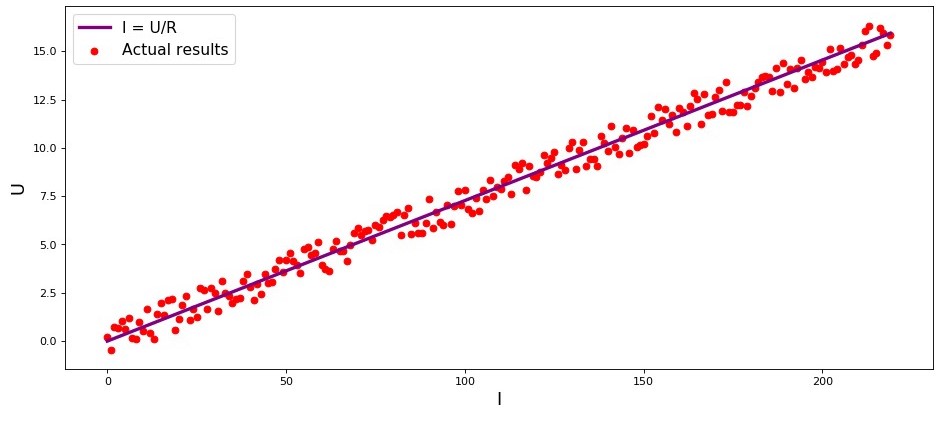
Código de representación gráficaimport matplotlib.pyplot as plt %matplotlib inline import numpy as np import random R = 13.75 x_line = np.arange(0,220,1) y_line = [] for i in x_line: y_line.append(i/R) y_dot = [] for i in y_line: y_dot.append(i+random.uniform(-0.9,0.9)) fig, axes = plt.subplots(figsize = (14,6), dpi = 80) plt.plot(x_line,y_line,color = 'purple',lw = 3, label = 'I = U/R') plt.scatter(x_line,y_dot,color = 'red', label = 'Actual results') plt.xlabel('I', size = 16) plt.ylabel('U', size = 16) plt.legend(prop = {'size': 14}) plt.show()
02. La necesidad de transformaciones de la ecuación de regresión lineal.
Considere otro ejemplo. Imagine que trabajamos en un banco y nos enfrentamos a la tarea de determinar la probabilidad de que un prestatario reembolse un préstamo, dependiendo de algunos factores. Para simplificar la tarea, consideramos solo dos factores: el salario mensual del prestatario y el pago mensual por el reembolso del préstamo.
La tarea es muy condicional, pero con este ejemplo podemos entender por qué no es suficiente usar
la función de regresión lineal para resolverla, y también descubriremos qué transformaciones con la función es necesario llevar a cabo.
Regresamos por ejemplo. Se entiende que cuanto mayor sea el salario, más podrá el prestatario dirigir mensualmente para pagar el préstamo. Al mismo tiempo, para un cierto rango de salarios, esta dependencia será bastante lineal por sí misma. Por ejemplo, tome un rango de salario de 60,000 a 200,000 y suponga que en el rango de salarios indicado, la dependencia del monto del pago mensual de la cantidad de salario es lineal. Supongamos que, para el rango de salarios especificado, se reveló que la proporción de salario a pago no puede caer por debajo de 3 y que el prestatario aún debe tener 5.000 en reserva. Y solo en este caso, asumiremos que el prestatario devolverá el préstamo al banco. Entonces, la ecuación de regresión lineal toma la forma:
f(w,xi)=w0+w1xi1+w2xi2,donde
w0=−5.000 ,
w1=1 ,
w2=−3 ,
xi1 -
salario i prestatario
xi2 -
pago del préstamo i prestatario
Sustituyendo el pago de salario y préstamo con parámetros fijos en la ecuación
vecw Puede decidir si otorga o rechaza un préstamo.
Mirando hacia el futuro, notamos que, para parámetros dados
vecw La función de regresión lineal utilizada en
la función de respuesta logística producirá grandes valores que dificultarán el cálculo de las probabilidades de reembolso del préstamo. Por lo tanto, se propone reducir nuestros coeficientes, digamos, 25,000 veces. A partir de esta conversión en ratios, la decisión de otorgar un préstamo no cambiará. Recordemos este momento para el futuro, y ahora para aclarar aún más de qué estamos hablando, consideraremos la situación con tres prestatarios potenciales.
Cuadro 1 "Prestatarios potenciales"
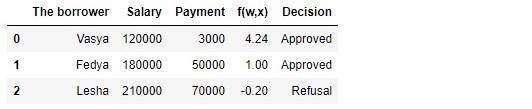
Código para generar la tabla import pandas as pd r = 25000.0 w_0 = -5000.0/r w_1 = 1.0/r w_2 = -3.0/r data = {'The borrower':np.array(['Vasya', 'Fedya', 'Lesha']), 'Salary':np.array([120000,180000,210000]), 'Payment':np.array([3000,50000,70000])} df = pd.DataFrame(data) df['f(w,x)'] = w_0 + df['Salary']*w_1 + df['Payment']*w_2 decision = [] for i in df['f(w,x)']: if i > 0: dec = 'Approved' decision.append(dec) else: dec = 'Refusal' decision.append(dec) df['Decision'] = decision df[['The borrower', 'Salary', 'Payment', 'f(w,x)', 'Decision']]
Según la tabla, Vasya, con un salario de 120,000, quiere obtener dicho préstamo para pagarlo a 3.000 mensualmente. Determinamos que para aprobar el préstamo, el salario de Vasya debería ser tres veces el monto del pago, y para que todavía hubiera 5.000P. Vasya cumple este requisito:
120.000−3∗3.000−5.000=106.000 . Queda incluso 106,000P. A pesar de que al calcular
f(w,xi) redujimos las probabilidades
vecw 25,000 veces, el resultado fue el mismo: el préstamo puede ser aprobado. Fedya también recibirá un préstamo, pero Lesha, a pesar del hecho de que recibe más, tendrá que contener su apetito.
Dibujemos un cronograma para este caso.
Gráfico 2 "Clasificación de los prestatarios"
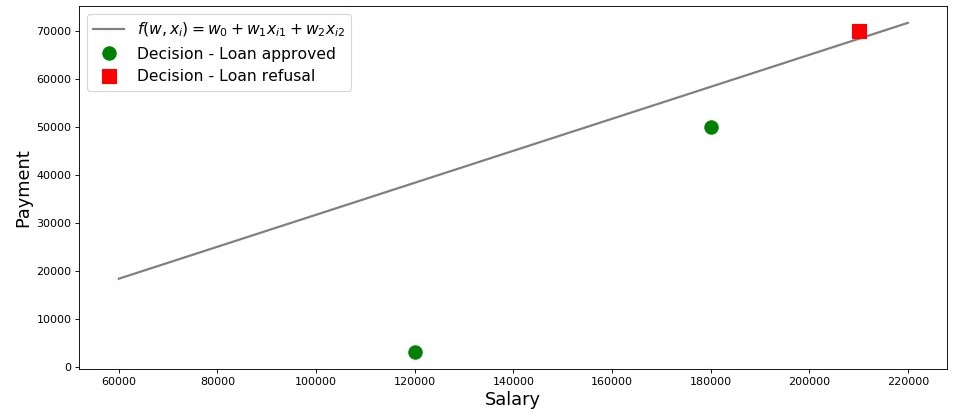
Código para trazar salary = np.arange(60000,240000,20000) payment = (-w_0-w_1*salary)/w_2 fig, axes = plt.subplots(figsize = (14,6), dpi = 80) plt.plot(salary, payment, color = 'grey', lw = 2, label = '$f(w,x_i)=w_0 + w_1x_{i1} + w_2x_{i2}$') plt.plot(df[df['Decision'] == 'Approved']['Salary'], df[df['Decision'] == 'Approved']['Payment'], 'o', color ='green', markersize = 12, label = 'Decision - Loan approved') plt.plot(df[df['Decision'] == 'Refusal']['Salary'], df[df['Decision'] == 'Refusal']['Payment'], 's', color = 'red', markersize = 12, label = 'Decision - Loan refusal') plt.xlabel('Salary', size = 16) plt.ylabel('Payment', size = 16) plt.legend(prop = {'size': 14}) plt.show()
Entonces, nuestra línea, construida de acuerdo con la función
f(w,xi)=w0+w1xi1+w2xi2 , separa a los prestatarios "malos" de los "buenos". Los prestatarios cuyos deseos no coinciden con las oportunidades están por encima de la línea directa (Lesha), aquellos que pueden pagar el préstamo de acuerdo con los parámetros de nuestro modelo están bajo la línea directa (Vasya y Fedya). De lo contrario, podemos decir esto: nuestra línea divide a los prestatarios en dos clases. Los denotamos de la siguiente manera: a la clase
+1 clasificar a aquellos prestatarios que probablemente reembolsen el préstamo a la clase
−1 o
0 asignaremos a los prestatarios que probablemente no podrán pagar el préstamo.
Resuma las conclusiones de este simple ejemplo. Toma un punto
M(x1,x2) y, sustituyendo las coordenadas del punto en la ecuación correspondiente de la línea
f(w,xi)=w0+w1xi1+w2xi2 , considere tres opciones:
- Si el punto está debajo de la línea, y lo asignamos a la clase +1 , entonces el valor de la función f(w,xi)=w0+w1xi1+w2xi2 será positivo de 0 antes + infty . Por lo tanto, podemos suponer que la probabilidad de reembolso del préstamo está dentro de (0.5,1] . Cuanto mayor sea el valor de la función, mayor será la probabilidad.
- Si el punto está por encima de la línea y lo relacionamos con la clase −1 o 0 , entonces el valor de la función será negativo de 0 antes − infty . Luego asumiremos que la probabilidad de pago de la deuda está dentro de [0,0.5) y, cuanto mayor sea el valor del módulo de función, mayor será nuestra confianza.
- El punto está en una línea recta, en el límite entre dos clases. En este caso, el valor de la función f(w,xi)=w0+w1xi1+w2xi2 será igual 0 y la probabilidad de reembolso del préstamo es igual a 0.5 .
Ahora, imagine que no tenemos dos factores, sino decenas, prestatarios no tres, sino miles. Luego, en lugar de una línea recta, tendremos un plano
m-dimensional y coeficientes
w no se nos tomará del techo, sino que se retirará de acuerdo con todas las reglas, sino sobre la base de los datos acumulados sobre prestatarios que devolvieron o no devolvieron el préstamo. Y realmente, fíjate, ahora estamos seleccionando prestatarios con índices ya conocidos
w . De hecho, la tarea del modelo de regresión logística es precisamente determinar los parámetros.
w en el cual el valor de la función de pérdida
La pérdida logística tenderá a un mínimo. Pero cómo se calcula el vector
vecw , todavía lo descubrimos en la quinta sección del artículo. Mientras tanto, regresamos a la tierra prometida, a nuestro banquero y sus tres clientes.
Gracias a la función
f(w,xi)=w0+w1xi1+w2xi2 sabemos a quién se le puede otorgar un préstamo y a quién se le debe negar. Pero no puede acudir al director con esa información, porque querían obtener la probabilidad de reembolso del préstamo de cada prestatario de nosotros. Que hacer La respuesta es simple: necesitamos transformar de alguna manera la función
f(w,xi)=w0+w1xi1+w2xi2 cuyos valores se encuentran en el rango
(− infty,+ infty) en una función cuyos valores estarán en el rango
[0,1] . Y tal función existe, se llama
función de respuesta logística o conversión de logit inverso . Cumplir:
sigma( vecwT vecxi)= frac11+e− vecwT vecxi
Echemos un vistazo a los pasos para obtener
la función de respuesta logística . Tenga en cuenta que avanzaremos en la dirección opuesta, es decir, suponemos que conocemos el valor de la probabilidad, que se encuentra en el rango de
0 antes
1 y luego "giraremos" este valor en todo el rango de números desde
− infty antes
+ infty .
03. Salida de la función de respuesta logística
Paso 1. Transfiera los valores de probabilidad al rango [0,+ infty)
En el momento de la transformación de la función.
f(w,xi)=w0+w1xi1+w2xi2 a
la función de respuesta logística sigma( vecwT vecxi)= frac11+e vecwT vecxi dejaremos en paz a nuestro analista de crédito y, en cambio, revisaremos las casas de apuestas. No, por supuesto, no haremos apuestas, lo único que nos interesa es el significado de la expresión, por ejemplo, una posibilidad de 4 a 1. Las probabilidades familiares para todos los jugadores de apuestas son la proporción de "éxitos" a "fracasos". En términos de probabilidades, las probabilidades son la probabilidad de que ocurra un evento dividido por la probabilidad de que el evento no ocurra. Escribimos la fórmula para la posibilidad de un evento.
(cuotas+) :
odds+= fracp+1−p+
donde
p+ - probabilidad de ocurrencia de un evento,
(1−p+) - probabilidad de ocurrencia de evento NOT
Por ejemplo, si la probabilidad de que un caballo joven, fuerte y alegre, apodado "Veterok" venza en las carreras, una anciana vieja y flácida apodada "Matilda" es igual a
0.8 , entonces las posibilidades de éxito de Veterka serán
4 a
1(0.8/(1−0.8)) y viceversa, conociendo las posibilidades, no será difícil para nosotros calcular la probabilidad
p+ :
fracp+1−p+=4 mkern15mu Longrightarrow mkern15mup+=4(1−p+) mkern15mu Longrightarrow mkern15mu5p+=4 mkern15mu Longrightarrow mkern15mup+=0.8Por lo tanto, hemos aprendido a "traducir" la probabilidad en probabilidades que toman valores de
0 antes
+ infty . Vamos a dar un paso más y aprender a "traducir" la probabilidad a la recta numérica entera de
− infty antes
+ infty .
Paso 2. Traducimos los valores de probabilidad al rango (− infty,+ infty)
Este paso es muy simple: prologamos las probabilidades según el número de Euler
e y obtener:
f(w,xi)= vecwT vecx=ln(probabilidades+)
Ahora sabemos que si
p+=0.8 luego calcule el valor
f(w,xi) será muy simple y, además, debería ser positivo:
f(w,xi)=ln(probabilidades+)=ln(0.8/0.2)=ln(4) aprox+1.38629 . Así es
En aras de la curiosidad, comprobamos que si
p+=0.2 entonces esperamos ver un valor negativo
f(w,xi) . Comprobamos:
f(w,xi)=ln(0.2/0.8)=ln(0.25) aprox−1.38629 . De acuerdo
Ahora sabemos cómo traducir el valor de probabilidad de
0 antes
1 en la recta numérica entera de
− infty antes
+ infty . En el siguiente paso, haremos lo contrario.
Mientras tanto, notamos que de acuerdo con las reglas del logaritmo, conocer el valor de la función
f(w,xi) , puedes calcular las probabilidades:
odds+=ef(w,xi)=e vecwT vecx
Este método para determinar las posibilidades será útil en el siguiente paso.
Paso 3. Derivamos una fórmula para determinar p+
Entonces aprendimos, sabiendo
p+ encontrar valores de funciones
f(w,xi) . Sin embargo, de hecho, necesitamos todo exactamente lo contrario: conocer el valor
f(w,xi) encontrar
p+ . Para hacer esto, recurrimos a un concepto como la función inversa de las oportunidades, de acuerdo con la cual:
p+= fracodds+1+odds+
En el artículo no derivaremos la fórmula anterior, sino que verificaremos los números del ejemplo anterior. Sabemos que con probabilidades de 4 a 1 (
cuotas+=$ ), la probabilidad de que ocurra un evento es 0.8 (
p+=0.8 ) Hagamos una sustitución:
p+= frac41+4=0.8 . Esto coincide con nuestros cálculos realizados anteriormente. Seguimos adelante.
En el último paso, dedujimos que
odds+=e vecwT vecx , lo que significa que puede realizar una sustitución en la función inversa de las probabilidades. Obtenemos:
p+= frace vecwT vecx1+e vecwT vecx
Divide tanto el numerador como el denominador entre
e vecwT vecx entonces:
p+= frac11+e− vecwT vecx= sigma( vecwT vecx)
Para cada bombero, para asegurarnos de que no hemos cometido un error en ningún lado, haremos un pequeño cheque más. En el paso 2, estamos para
p+=0.8 determinado que
f(w,xi) aprox+1.38629 . Luego, sustituyendo el valor
f(w,xi) en la función de respuesta logística, esperamos obtener
p+=0.8 . Sustituir y obtener:
p+= frac11+e−1.38629=0.8Felicitaciones, querido lector, acabamos de desarrollar y probar la función de respuesta logística. Veamos el gráfico de funciones.
Gráfico 3 "Función de respuesta logística"

Código para trazar import math def logit (f): return 1/(1+math.exp(-f)) f = np.arange(-7,7,0.05) p = [] for i in f: p.append(logit(i)) fig, axes = plt.subplots(figsize = (14,6), dpi = 80) plt.plot(f, p, color = 'grey', label = '$ 1 / (1+e^{-w^Tx_i})$') plt.xlabel('$f(w,x_i) = w^Tx_i$', size = 16) plt.ylabel('$p_{i+}$', size = 16) plt.legend(prop = {'size': 14}) plt.show()
En la literatura, también puede encontrar el nombre de esta función como una
función sigmoidea . El gráfico muestra claramente que el cambio principal en la probabilidad de pertenencia de un objeto a una clase ocurre en un rango relativamente pequeño
f(w,xi) en algún lugar de
−4 antes
+4 .
Propongo volver a nuestro analista de crédito y ayudarlo a calcular la probabilidad de reembolso de los préstamos, de lo contrario corre el riesgo de quedarse sin un bono :)
Cuadro 2 "Prestatarios potenciales"
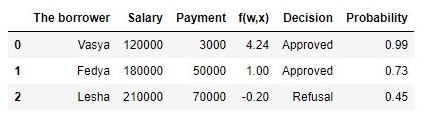
Código para generar la tabla proba = [] for i in df['f(w,x)']: proba.append(round(logit(i),2)) df['Probability'] = proba df[['The borrower', 'Salary', 'Payment', 'f(w,x)', 'Decision', 'Probability']]
Entonces, determinamos la probabilidad de reembolso del préstamo. En general, esto parece ser cierto.
De hecho, la probabilidad de que Vasya con un salario de 120,000 pueda dar 3.000 mensualmente al banco es cercana al 100%. Por cierto, debemos entender que un banco puede otorgar un préstamo a Lesha si la política del banco establece, por ejemplo, prestar a clientes con una probabilidad de reembolso de un préstamo de más, digamos, 0.3. Solo en este caso, el banco formará una reserva más grande para posibles pérdidas.
También se debe tener en cuenta que la proporción de salario a pago de al menos 3 y con un margen de 5.000 se tomó del techo. Por lo tanto, no podríamos usar el vector de peso en su forma original
vecw=(−5000,1,−3) . Necesitábamos reducir en gran medida los coeficientes, y en este caso dividimos cada coeficiente por 25,000, es decir, ajustamos el resultado. Pero esto se hizo a propósito para simplificar la comprensión del material en la etapa inicial. En la vida, no necesitamos inventar y ajustar los coeficientes, sino encontrarlos. Solo en las siguientes secciones del artículo derivaremos las ecuaciones con las que se seleccionan los parámetros
vecw .
04. Método de mínimos cuadrados para determinar el vector de pesos vecw en la función de respuesta logística
Ya conocemos un método para seleccionar un vector de peso.
vecw como
el método de mínimos cuadrados (OLS) y, de hecho, ¿por qué no lo usamos en problemas de clasificación binaria? De hecho, nada impide el uso de las
empresas multinacionales , solo este método en problemas de clasificación proporciona resultados menos precisos que la
pérdida logística . Hay una justificación teórica para esto. Comencemos mirando un ejemplo simple.
Supongamos que nuestros modelos (usando
MSE y
Pérdida logística ) ya han comenzado la selección del vector de peso
vecw y detuvimos el cálculo en algún momento. No importa, en el medio, al final o al principio, lo principal es que ya tenemos algunos valores del vector de pesos y supongamos, en este paso, el vector de pesos
vecw para ambos modelos no tienen diferencias. Luego tomamos los pesos obtenidos y los sustituimos en
la función de respuesta logística (
frac11+e− vecwT vecx ) para algún objeto que pertenece a la clase
+1 . Investigaremos dos casos en los que, de acuerdo con el vector de pesos seleccionado, nuestro modelo esté muy equivocado y viceversa: el modelo confía firmemente en que el objeto pertenece a la clase
+1 . Veamos qué multas se "emitirán" cuando se usen
MNCs y
Logistic Loss .
Código para calcular multas dependiendo de la función de pérdida utilizada El caso con un error grave : el modelo clasifica el objeto
+1 con una probabilidad de 0.01
La penalización cuando se usa
OLS es:
MSE=(y−p+)=(1−0.01)2=0.9801La penalización cuando se utiliza la
pérdida logística es:
LogLoss=loge(1+e−yf(w,x))=loge(1+e−1(−4.595...)) aprox4.605Caso con certeza firme : el modelo clasifica el objeto
+1 con una probabilidad de 0.99
La penalización cuando se usa
OLS es:
MSE=(1−0.99)2=$0.000La penalización cuando se utiliza la
pérdida logística es:
LogLoss=loge(1+e−4.595...) aproximadamente0.01Este ejemplo ilustra bien que con un error grave, la función de pérdida de
pérdida de registro multa al modelo significativamente más que
MSE . Ahora comprendamos cuáles son los requisitos previos teóricos para usar la función de pérdida de
pérdida de registro en problemas de clasificación.
05. Método de máxima credibilidad y regresión logística
Como se prometió al principio, el artículo abunda en ejemplos simples. En el estudio, otro ejemplo y antiguos invitados son los prestatarios del banco: Vasya, Fedya y Lesha.
Por cada bombero, antes de desarrollar un ejemplo, permíteme recordarte que en la vida estamos tratando con una muestra de entrenamiento de miles o millones de objetos con decenas o cientos de signos. Sin embargo, aquí se toman los números para que quepan fácilmente en la cabeza de un datasintest novato.
Regresamos por ejemplo. Imagine que el director del banco decidió otorgar un préstamo a todos los necesitados, a pesar de que el algoritmo sugirió no otorgarlo a Lesha. Y así pasó el tiempo suficiente y nos dimos cuenta de cuál de los tres héroes reembolsó el préstamo y quién no. Lo que se esperaba: Vasya y Fedya pagaron el préstamo, pero Alex no. Ahora imaginemos que este resultado será una nueva muestra de capacitación para nosotros y, al mismo tiempo, todos los datos sobre los factores que afectan la probabilidad de reembolso del préstamo (salario del prestatario, monto del pago mensual) parecen haber desaparecido. Entonces, intuitivamente, podemos suponer que cada tercer prestatario no devuelve un préstamo al banco, o en otras palabras, la probabilidad de que el próximo prestatario devuelva un préstamo
p= frac23 . Existe evidencia teórica de esta suposición intuitiva y se basa en el
método de máxima verosimilitud , a menudo referido en la literatura como
el principio de máxima verosimilitud .
Primero, familiarícese con el aparato conceptual.
La probabilidad de una
muestra es la probabilidad de obtener tal muestra, de obtener precisamente tales observaciones / resultados, es decir El producto de las probabilidades de obtener cada uno de los resultados de la muestra (por ejemplo, el préstamo de Vasya, Feday y Lesha al mismo tiempo se reembolsó o no).
La función de probabilidad asocia la probabilidad de una muestra con los valores de los parámetros de distribución.
En nuestro caso, la muestra de entrenamiento es un esquema generalizado de Bernoulli en el que una variable aleatoria toma solo dos valores:
1 o
0 . Por lo tanto, la probabilidad de la muestra se puede escribir en función de la probabilidad del parámetro
p como sigue:
P( mkern5mu vecy mkern5mu| mkern5mup)= prod limits3i=1pyi(1−p)(1−yi) mkern5mu= mkern5mup1(1−p)1−1 centerdotp1(1−p)1−1 centerdotp0(1−p)1−0 mkern5mu== mkern5mup centerdotp centerdot(1−p) mkern5mu= mkern5mup2(1−p)El registro anterior se puede interpretar de la siguiente manera. La probabilidad conjunta de que Vasya y Fedya reembolsen el préstamo es igual a
p centerdotp=p2 , la probabilidad de que Alex NO reembolse el préstamo es
1−p (dado que NO fue el reembolso del préstamo), por lo tanto, la probabilidad conjunta de los tres eventos es
p2(1−p) .
El método de
máxima verosimilitud es un método para estimar un parámetro desconocido al maximizar
la función de verosimilitud .
En nuestro caso, necesitamos encontrar ese valor p en que P(→y|p)=p2(1−p)alcanza un maximo.¿De dónde viene la idea: buscar el valor de un parámetro desconocido en el que la función de probabilidad alcanza un máximo? Los orígenes de la idea se derivan de la noción de que el muestreo es la única fuente de conocimiento disponible para nosotros sobre la población en general. Todo lo que sabemos sobre la población se presenta en la muestra. Por lo tanto, todo lo que podemos decir es que la muestra es el reflejo más preciso de la población que tenemos disponible. Por lo tanto, necesitamos encontrar un parámetro en el que la muestra disponible se convierta en la más probable.Obviamente, estamos lidiando con un problema de optimización en el que se requiere encontrar el punto extremo de una función. Para encontrar el punto extremo, es necesario considerar una condición de primer orden, es decir, equiparar la derivada de la función a cero y resolver la ecuación con respecto al parámetro deseado. Sin embargo, la búsqueda de la derivada de un producto de una gran cantidad de factores puede ser larga, por lo que existe una técnica especial para evitar esto: la transición al logaritmo de la función de probabilidad . ¿Por qué es posible tal transición? Prestamos atención al hecho de que no estamos buscando el extremo de la función en síP(→y|p) y el punto extremo, es decir, el valor del parámetro desconocido p en que P(→y|p)alcanza un maximo. Tras la transición al logaritmo, el punto extremo no cambia (aunque el extremo en sí será diferente), ya que el logaritmo es una función monotónica.De acuerdo con lo anterior, continuemos desarrollando nuestro ejemplo de préstamos con Vasya, Fedi y Lesha. Primero, pasemos al logaritmo de la función de probabilidad :logP(→y|p)=logp2(1−p)=2logp+log(1−p)Ahora podemos diferenciar fácilmente una expresión por p :
∂logP(→y|p)∂p=∂∂p(2logp+log(1−p))=2p−11−pY finalmente, considere la condición de primer orden: equiparamos la derivada de la función a cero:2p−11−p=0⟹2p=11−p⟹2(1−p)=p⟹p=23Por lo tanto, nuestra evaluación intuitiva de la probabilidad de reembolso del préstamo p=23fue teóricamente justificado.Genial, pero ¿qué hacemos ahora con esta información? Si suponemos que cada tercer prestatario no devuelve dinero al banco, este último inevitablemente irá a la quiebra. Y así es, pero solo cuando se evalúa la probabilidad de reembolso de un préstamo igual a23No tomamos en cuenta los factores que afectan el reembolso del préstamo: el salario del prestatario y el monto del pago mensual. Recuerde que antes calculamos la probabilidad de reembolso del préstamo por cada cliente, teniendo en cuenta estos mismos factores. Es lógico que las probabilidades que tenemos sean diferentes de la constante igual a23 .
Determinemos la probabilidad de las muestras:Código para calcular la probabilidad de muestras from functools import reduce def likelihood(y,p): line_true_proba = [] for i in range(len(y)): ltp_i = p[i]**y[i]*(1-p[i])**(1-y[i]) line_true_proba.append(ltp_i) likelihood = [] return reduce(lambda a, b: a*b, line_true_proba) y = [1.0,1.0,0.0] p_log_response = df['Probability'] const = 2.0/3.0 p_const = [const, const, const] print ' p=2/3:', round(likelihood(y,p_const),3) print '****************************************************************************************************' print ' p:', round(likelihood(y,p_log_response),3)
La probabilidad de muestreo a un valor constante p=23 :P(→y|p)=p2(1−p)=232(1−23)≈0.148La probabilidad de muestreo al calcular la probabilidad de reembolso del préstamo teniendo en cuenta factores →x :P(→y|p)=3∏i=1pyi(1−p)(1−yi)=p11(1−p1)1−1⋅p12(1−p2)1−1⋅p03(1−p3)1−0==p1⋅p2⋅(1−p3)=0.99⋅0.73⋅(1−0.45)≈0.397La probabilidad de la muestra con probabilidad calculada según los factores fue mayor que la probabilidad con un valor constante de probabilidad. ¿De qué está hablando esto? Esto sugiere que el conocimiento de los factores permitió seleccionar con mayor precisión la probabilidad de reembolso del préstamo para cada cliente. Por lo tanto, al emitir otro préstamo, será más correcto usar el modelo para evaluar la probabilidad de reembolso de la deuda propuesta al final de la tercera sección del artículo.Pero entonces, si necesitamos maximizar la función de probabilidad de la muestra, entonces, ¿por qué no utilizar un algoritmo que proporcione las probabilidades para Vasya, Fedi y Lesha, por ejemplo, igual a 0.99, 0.99 y 0.01, respectivamente. Quizás tal algoritmo se mostrará bien en la muestra de entrenamiento, ya que acercará el valor de la probabilidad de la muestra a1, pero, en primer lugar, un algoritmo de este tipo probablemente tendrá dificultades con la capacidad de generalización, y en segundo lugar, este algoritmo definitivamente no será lineal. Y si los métodos para tratar el reciclaje (capacidad de generalización igualmente débil) claramente no se incluyen en el plan de este artículo, entonces veamos el segundo párrafo con más detalle. Para hacer esto, solo responda una pregunta simple. ¿Puede la probabilidad de pagar un préstamo a Vasya y Feday ser la misma, teniendo en cuenta los factores que conocemos? Desde el punto de vista de la lógica del sonido, por supuesto que no, no puede. Entonces, Vasya dará el 2.5% de su salario por mes para pagar el préstamo, y Fedya, casi el 27.8%. También en el gráfico 2 “Clasificación de clientes” vemos que Vasya está mucho más lejos de la línea que separa clases que Fedya. Y finalmente, sabemos que la funciónf(w,x)=w0+w1x1+w2x2para Vasya y Fedi tiene diferentes significados: 4.24 para Vasya y 1.0 para Fedi. Ahora, si Fedya, por ejemplo, gana un orden de magnitud más o solicita un préstamo más pequeño, entonces las probabilidades de pagar el préstamo de Vasya y Fedi serían similares. En otras palabras, una relación lineal no puede ser engañada. Y si realmente calculamos las probabilidadesw , pero no los tomamos del techo, podríamos declarar con seguridad que nuestros valores w mejor le permite evaluar la probabilidad de reembolso del préstamo por cada prestatario, pero dado que acordamos considerar que la determinación de los coeficientes wse llevó a cabo de acuerdo con todas las reglas, luego lo consideraremos así: nuestros coeficientes nos permiten dar una mejor estimación de la probabilidad :)Sin embargo, estábamos distraídos. En esta sección, necesitamos entender cómo se determina el vector de pesos→w, que es necesario para evaluar la probabilidad de que un prestatario devuelva un préstamo.Resuma brevemente qué arsenal buscamos cuotasw :
1. Suponemos que la relación entre la variable objetivo (valor de pronóstico) y el factor que influye en el resultado es lineal. Por esta razón, se utiliza la función de regresión lineal del formulario.f(w,x)=→wTX cuya línea divide los objetos (clientes) en clases +1 y
−1 o
0(clientes que pueden pagar el préstamo y no pueden). En nuestro caso, la ecuación tiene la formaf(w,x)=w0+w1x1+w2x2 .
2. Usamos la función de transformación de registro inverso de la formap+=11+e−→wT→x=σ(→wT→x) para determinar la probabilidad de que un objeto pertenezca a una clase +1 .
3. Consideramos nuestra muestra de entrenamiento como la implementación de un esquema generalizado de Bernoulli , es decir, para cada objeto se genera una variable aleatoria, que es probablep (propio para cada objeto) toma el valor 1 y con probabilidad (1–p)- 0.4. Sabemos que necesitamos maximizar la función de probabilidad de la muestra , teniendo en cuenta los factores aceptados, para que la muestra existente sea la más probable. En otras palabras, necesitamos seleccionar los parámetros en los cuales la muestra será la más plausible. En nuestro caso, el parámetro seleccionado es la probabilidad de reembolso del préstamo.p , que a su vez depende de coeficientes desconocidos w .
Entonces necesitamos encontrar un vector de pesos →wen el cual la probabilidad de la muestra será máxima.5. Sabemos que para maximizar la función de probabilidad de una muestra, puede usar el método de máxima probabilidad . Y conocemos todos los trucos para trabajar con este método.Aquí hay una ruta múltiple :)Y ahora recuerde que al comienzo del artículo queríamos derivar dos tipos de la función de pérdida de pérdida logística , dependiendo de cómo se designen las clases de objetos. Sucedió que en problemas de clasificación con dos clases, las clases se denotan como+1 y
0 o
−1 .
Dependiendo de la designación, la salida tendrá una función de pérdida correspondiente.Caso 1. Clasificación de objetos en +1 y 0
Anteriormente, al determinar la probabilidad de una muestra en la que la probabilidad de reembolso de la deuda por parte del prestatario se calculó en función de factores y coeficientes específicos w , aplicamos la fórmula:P(→y|p)=3∏i=1pyi(1−p)(1−yi)De hecho piEs el valor de la función de respuesta logística. p+=11+e−→wT→x=σ(→wT→x) para un vector de peso dado →wEntonces nada nos impide escribir la función de probabilidad de la muestra de esta manera:P(→y|σ(→wTX))=n∏i=1σ(→wT→xi)yi(1−σ(→wT→xi)(1−yi)→max
Ocurre que a veces, para algunos analistas novatos, es difícil entender de inmediato cómo funciona esta función. Veamos 4 ejemplos cortos que aclararán todo:1. Siyi=+1 (es decir, de acuerdo con la muestra de entrenamiento, el objeto pertenece a la clase +1) y nuestro algoritmo σ(→wTX)) determina la probabilidad de clasificar un objeto +1 igual a 0.9, entonces esta parte de la probabilidad de la muestra se calculará de la siguiente manera:0.91⋅(1−0.9)(1−1)=0.91⋅0.10=0.92. Siyi=+1 y σ(→wTX))=0.1 , entonces el cálculo será así:0.11⋅(1−0.1)(1−1)=0.11⋅0.90=0.13. Siyi=0 y σ(→wTX))=0.1 , entonces el cálculo será así:0.10⋅(1−0.1)(1−0)=0.10⋅0.91=0.94. Siyi=0 y σ(→wTX))=0.9 , entonces el cálculo será así:0.90⋅(1−0.9)(1−0)=0.90⋅0.11=0.1Obviamente, la función de probabilidad se maximizará en los casos 1 y 3, o en el caso general, con valores correctamente adivinados de las probabilidades de clasificar un objeto como clase +1 .
Debido al hecho de que al determinar la probabilidad de clasificar un objeto como una clase +1 no sabemos solo los coeficientes w, luego los buscaremos. Como se mencionó anteriormente, este es un problema de optimización en el que primero necesitamos encontrar la derivada de la función de probabilidad con respecto al vector de pesow .
Sin embargo, tiene sentido simplificar la tarea primero: buscaremos la derivada del logaritmo de la función de probabilidad .Llog(X,→y,→w)=n∑i=1(−yilogeσ(→wT→xi)−(1−yi)loge(1−σ(→wT→xi)))→min
¿Por qué, después del logaritmo, en función del error logístico , cambiamos el signo con+ en
− .
Todo es simple, ya que es habitual minimizar el valor de una función en problemas de evaluación de la calidad del modelo, multiplicamos el lado derecho de la expresión por −y, en consecuencia, en lugar de maximizar, ahora minimizamos la función.En realidad, ahora, ante sus propios ojos, la función de pérdida: la pérdida logística para el conjunto de entrenamiento con dos clases se vio muy afectada .+1 y
0 .
Ahora, para encontrar los coeficientes, solo necesitamos encontrar la derivada de la función de error logístico y luego, utilizando métodos de optimización numérica, como el descenso de gradiente o el descenso de gradiente estocástico, seleccione los coeficientes más óptimosw .
Pero, dado el tamaño ya pequeño del artículo, se propone diferenciar de manera independiente o, tal vez, este será el tema para el próximo artículo con mucha aritmética sin ejemplos tan detallados.Caso 2. Clasificación de objetos en +1 y −1
El enfoque aquí será el mismo que con las clases. 1 y
0pero el camino en sí a la salida de la función de pérdida de pérdida logística será más recargado. Bajando Para la función de verosimilitud, utilizamos el operador "si ... entonces ..." . Es decir, sii el objeto pertenece a la clase +1 , luego para calcular la probabilidad de la muestra, usamos la probabilidad p si el objeto pertenece a la clase −1 , luego en el verosimilitud sustituto (1−p) .
Así es como se ve la función de probabilidad:P(→y|σ(→wTX))=n∏i=1σ(→wT→xi)[yi=+1](1−σ(→wT→xi)[yi=−1])→max
Escribiremos en los dedos cómo funciona esto. Considere 4 casos:1. Siyi=+1 y
σ(→wT→xi)=0.9 , luego en la verosimilitud de la muestra "ir" 0.92. Siyi=+1 y
σ(→wT→xi)=0.1 , luego en la verosimilitud de la muestra "ir" 0.13. Siyi=−1 y
σ(→wT→xi)=0.1 , luego en la verosimilitud de la muestra "ir" 1−0.1=0.94. Siyi=−1 y
σ(→wT→xi)=0.9 , luego en la verosimilitud de la muestra "ir" 1−0.9=0.1Obviamente, en los casos 1 y 3, cuando las probabilidades fueron determinadas correctamente por el algoritmo, la función de probabilidad se maximizará, eso es exactamente lo que queríamos obtener. Sin embargo, este enfoque es bastante engorroso, y consideraremos una grabación más compacta a continuación. Pero primero, el logaritmo de la probabilidad funciona con un cambio de signo, ya que ahora lo minimizaremos.Llog(X,→y,→w)=n∑i=1(−[yi=+1]logeσ(→wT→xi)−[yi=−1]loge(1−σ(→wT→xi)))→min
Sustituir en su lugar σ(→wT→xi) expresión 11+e−→wT→xi :
Llog(X,→y,→w)=n∑i=1(−[yi=+1]loge(11+e−→wT→xi)−[yi=−1]loge(1−11+e−→wT→xi))→min
Simplifique el término correcto debajo del logaritmo usando técnicas aritméticas simples y obtenga:Llog(X,→y,→w)=n∑i=1(−[yi=+1]loge(11+e−→wT→xi)−[yi=−1]loge(11+e→wT→xi))→min
Y ahora es el momento de deshacerse del operador "si ... entonces ..." . Tenga en cuenta que cuando un objetoyi pertenece a la clase +1 , luego en la expresión debajo del logaritmo, en el denominador, e elevado al poder −→wT→xi si el objeto pertenece a la clase −1 entonces $ e $ se eleva a una potencia +→wT→xi .
Por lo tanto, escribir un título se puede simplificar combinando ambos casos en uno: −yi→wT→xi .
Entonces la función de error logístico toma la forma:Llog(X,→y,→w)=n∑i=1−loge(11+e−yi→wT→xi)→min
De acuerdo con las reglas del logaritmo, voltea la fracción y saca el signo " − "(menos) por logaritmo, obtenemos:Llog(X,→y,→w)=n∑i=1loge(1+e−yi→wT→xi)→min
Aquí está la función de pérdida Pérdida logística , que se utiliza en el conjunto de entrenamiento con objetos relacionados con las clases:+1 y
−1 .
Bueno, en este punto me despido y terminamos el artículo.← El trabajo anterior del autor: "Traemos la ecuación de regresión lineal en forma de matriz"Materiales de apoyo
1. literatura
1) Análisis de regresión aplicado / N. Draper, G. Smith - 2ª ed. - M .: Finanzas y Estadística, 1986 (traducido del inglés)2) Teoría de la probabilidad y estadística matemática / V.E. Gmurman - 9a ed. - M .: Escuela Superior, 20033) Teoría de la probabilidad / N.I. Chernova - Novosibirsk: Universidad Estatal de Novosibirsk, 20074) Análisis de negocios: de los datos al conocimiento / Paklin N. B., Oreshkov V. I. - 2ª ed. - San Petersburgo: Peter, 20135) Ciencia de datos Ciencia de datos desde cero / Joel Grass - San Petersburgo: BHV Petersburgo, 20176) Estadísticas prácticas para especialistas en ciencia de datos / P. Bruce, E. Bruce - San Petersburgo: BHV Petersburgo, 20182. Conferencias, cursos (video)
1) La esencia del método de máxima verosimilitud, Boris Demeshev2) El método de máxima verosimilitud en el caso continuo, Boris Demeshev3) Regresión logística. Curso abierto ODS, Yury Kashnitsky4) Conferencia 4, Evgeny Sokolov (con 47 minutos de video)5) Regresión logística, Vyacheslav Vorontsov3. fuentes de Internet
1) Modelos lineales de clasificación y regresión2) Es fácil entender la regresión logística3) Función logística del error4) Pruebas independientes y fórmula de Bernoulli5) Balada del FMI6) Métodode máxima verosimilitud 7) Fórmulas y propiedades de los logaritmos8) ¿Por qué es el número? e ?9) clasificador lineal