En la víspera del inicio del curso "Matemáticas para la ciencia de datos". Curso avanzado ” realizamos un seminario web abierto sobre el tema“ Métodos de análisis de regresión en ciencia de datos ”. En él nos familiarizamos con el concepto de regresiones lineales, estudiamos dónde y cómo se pueden aplicar en la práctica, y también aprendimos qué temas y secciones de análisis matemático, álgebra lineal y teoría de probabilidad se utilizan en esta área. Profesor: Peter Lukyanchenko , profesor de la Escuela Superior de Economía, Jefe de Proyectos de Tecnología.
Si hablamos de matemáticas en el contexto de la ciencia de datos, podemos destacar los tres problemas resueltos con mayor frecuencia (aunque, por supuesto, hay más problemas):

Hablemos de estas tareas con más detalle:
- La tarea de análisis de regresión o identificación de dependencias (cuando tenemos un cierto conjunto de observaciones). En el gráfico anterior, puede ver que hay una determinada variable xy una determinada variable y, y observamos los valores de y para una x específica. Conocemos estos puntos y sus coordenadas, y también sabemos que x de alguna manera afecta a y, es decir, estas dos variables dependen unas de otras. Naturalmente, queremos calcular la ecuación de su dependencia; para esto utilizamos el modelo de regresión lineal de pares clásicos , cuando se supone que su dependencia puede describirse mediante una determinada línea recta. En consecuencia, los coeficientes de línea recta se seleccionan para minimizar el error en la descripción de los datos. Y solo de qué tipo de error (métrica de calidad) se seleccionará, el resultado real de construir una regresión lineal depende.
- Otra tarea del análisis de datos son los sistemas de recomendación . Esto es cuando decimos que hay, por ejemplo, tiendas en línea, tienen un cierto conjunto de productos y una persona realiza compras. Con base en esta información, es posible proporcionar una descripción de esta persona en el espacio vectorial y, una vez construido este espacio vectorial, construir una dependencia matemática de la probabilidad con la que esta persona comprará este o aquel producto, conociendo sus compras anteriores. En consecuencia, estamos hablando de clasificación cuando clasificamos a los compradores potenciales de acuerdo con los principios: "comprar-no comprar", "interesante-poco interesante", etc. Existen varios enfoques: basados en el usuario y basados en artículos.
- La tercera área es la visión por computadora . En el curso de esta tarea, estamos tratando de determinar dónde se encuentra el objeto de interés para nosotros. Esta es realmente una solución al problema de minimizar los errores seleccionando píxeles específicos que forman la imagen del objeto.
En los tres problemas, hay optimización, minimización de errores y la presencia de uno u otro modelo que describe la dependencia de las variables. Al mismo tiempo, dentro de cada uno se encuentra una representación de datos que se descompone en una descripción vectorial. En nuestro artículo, prestaremos especial atención a la sección que afecta a
los modelos de regresión .
Ya hemos mencionado que hay un cierto conjunto de pares de datos: X e Y. Sabemos qué valores toma Y con respecto a X. Si X es el tiempo, obtenemos un modelo de serie temporal en el que Y es, por ejemplo, el precio del petróleo. y al mismo tiempo, el tipo de cambio del rublo al dólar, y X es un cierto período de tiempo de 2014 a 2018:
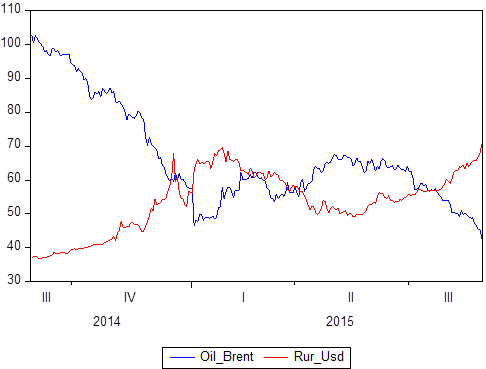
Si construye gráficamente, está claro que estas dos series de tiempo son interdependientes. Una vez definido el concepto de correlación, puede calcular el grado de su dependencia, y luego, si sabe que algunos valores están perfectamente correlacionados (la correlación es 1 o -1), puede usar esto para tareas de pronóstico o para tareas de descripción.
Considere la siguiente ilustración:
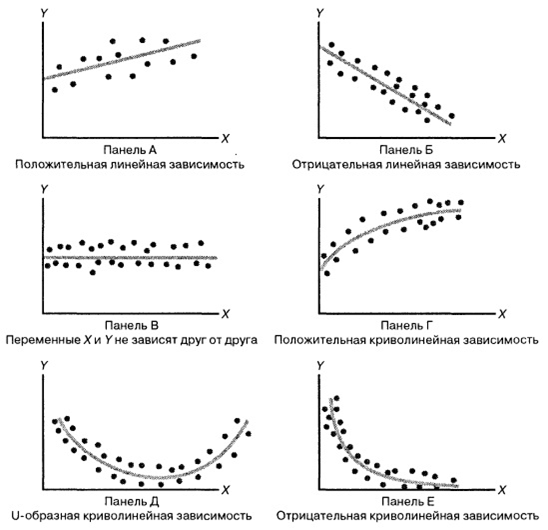
La parte más difícil en la formación de un modelo de regresión es
inicialmente poner alguna función específica en su memoria . Por ejemplo, para la Figura A es Y = kX + b, para B es Y = -kX + b, en la figura C el "juego" es igual a algún número, el gráfico de la figura D probablemente se basa en la raíz de " X ”, en la base de D, posiblemente una parábola, y en la base de E - una hipérbole.
Resulta que
elegimos algún modelo de dependencia de datos , y los tipos de dependencia entre variables aleatorias son diferentes. No todo es tan obvio, porque incluso en estos dibujos simples vemos varias dependencias. Al elegir una relación específica, podemos usar métodos de regresión para calibrar el modelo.
La calidad de sus pronósticos dependerá del modelo que elija . Si nos enfocamos en modelos de regresión lineal, entonces asumimos que hay un cierto conjunto de valores reales:

La figura muestra los 4 valores observados de X1, X2, X2, X4. Para cada una de las X, se conoce el valor Y (en nuestro caso, estos son los puntos: P1, P2, P3, P4). Estos son los puntos que realmente observamos en los datos. Por lo tanto, recibimos un determinado conjunto de datos. Y por alguna razón, decidimos que la regresión lineal describe mejor la relación entre la X y el jugador. Además, toda la pregunta es cómo construir la ecuación de una línea recta Y = b
1 + b
2 X, donde b
2 es el coeficiente de la pendiente, b
1 es el coeficiente de intersección. Toda la pregunta es qué b
2 y b
1 están mejor configurados para que esta línea recta describa la relación entre estas variables con la mayor precisión posible.
Los puntos R
1 , R
2 , R
3 , R
4 son los valores que nuestro modelo da a los valores de X. ¿Qué sucede? Los puntos P son puntos que realmente observamos (realmente recopilados), y los puntos R son puntos que observamos en nuestro modelo (los que produce). Lo que sigue es una lógica humana increíblemente simple: un
modelo se considerará cualitativo si y solo si los puntos R están lo más cerca posible de los puntos P.Si construimos la distancia entre estos puntos para la misma "X" (P
1 - R
1 , P
2 - R
2 , etc.), obtenemos lo que se llama errores de regresión lineal. Obtenemos las desviaciones en regresión lineal, y estas desviaciones se llaman U
1 , U
2 , U
3 ... U
n . Y estos errores pueden estar en más o menos (podríamos sobreestimar o subestimar). Para comparar estas desviaciones, deben analizarse. Aquí se usa un método muy grande y hermoso: cuadrar (cuadrar "mata" el signo). Y la suma de los cuadrados de todas las desviaciones en las estadísticas matemáticas se llama RSS (suma residual de cuadrados). Al minimizar RSS por b
1 y al minimizar RSS por b
2 , obtenemos coeficientes óptimos que en realidad se derivan
del método de mínimos cuadrados .
Después de construir la regresión, determinar los coeficientes óptimos b
1 y b
2 , y tenemos la ecuación de regresión, los problemas no terminan allí y el problema continúa desarrollándose. El hecho es que si la regresión misma está marcada en un gráfico, todos los valores que tenemos, así como los valores promedio de los "juegos", entonces la suma de los errores al cuadrado puede aclararse.
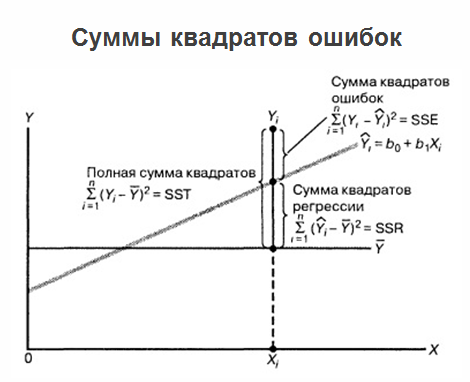
Al mismo tiempo, se considera útil mostrar errores de predicción de regresión con respecto a la variable X. Vea la figura a continuación:

Obtuvimos algún tipo de regresión y extrajimos los datos reales que son. Obtuvimos la distancia de cada valor real a la regresión. Y lo dibujamos en relación con el valor cero para los valores correspondientes de X. Y en la figura anterior vemos una imagen realmente mala: los
errores dependen de X. Cierta dependencia de correlación se expresa claramente: cuanto
más avanzamos a lo largo de la "X", mayor es la importancia de los errores . Esto es muy malo La presencia de correlación en este caso indica que tomamos por error el modelo de regresión, y había algún parámetro que "no pensamos" o simplemente perdimos de vista. Después de todo, si todas las variables se colocan dentro del modelo, los errores deberían ser completamente aleatorios y no deberían depender de qué factores son iguales.
Los errores deben tener la misma distribución de probabilidad , de lo contrario, sus predicciones serán erróneas. Si dibujó los errores de su modelo en un avión y se encontró con un triángulo divergente, es mejor comenzar todo desde cero y contar completamente el modelo.
Al analizar los errores, incluso puede comprender de inmediato dónde calcularon mal, qué tipo de error cometieron. Y aquí no podemos dejar de mencionar el teorema de Gauss-Markov:

El teorema determina las condiciones bajo las cuales las estimaciones obtenidas por el método de mínimos cuadrados son las mejores, consistentes y efectivas en la clase de estimaciones lineales insesgadas.
La conclusión se puede extraer de la siguiente manera: ahora entendemos que el
área de construcción de un modelo de regresión es, en cierto sentido, la culminación desde el punto de vista de las matemáticas , porque combina todas las secciones posibles a la vez, lo que puede ser útil en el análisis de datos, por ejemplo:
- álgebra lineal con métodos de representación de datos;
- análisis matemático con teoría de optimización y medios de análisis de funciones;
- teoría de probabilidad con medios para describir eventos y cantidades aleatorias y modelar la relación entre variables.
Colegas, sugiero lo mismo, sin limitarse a leer y ver todo el seminario web . El artículo no incluyó momentos relacionados con la programación lineal, la optimización en modelos de regresión y otros detalles que pueden serle útiles.