🗯️ ☔️ ❄️ सामान्य कानून के अनुसार वितरित एक बहुआयामी डेटा सरणी मॉडलिंग के लिए एल्गोरिदम 👉🏿 🌙 💅🏿

तैयार किए गए एल्गोरिदम को विकसित या शोध करते समय, अक्सर उनके काम की गुणवत्ता निर्धारित करने के लिए आवश्यक होता है। इस उद्देश्य के लिए वास्तविक स्रोतों से डेटा का उपयोग करना हमेशा संभव नहीं होता है, क्योंकि उनके गुण अक्सर अज्ञात होते हैं और इसलिए जांच किए गए एल्गोरिदम के परिणाम की भविष्यवाणी करना असंभव है। इस मामले में, डेटा मॉडलिंग प्रसिद्ध वितरण कानूनों में से एक के अनुसार लागू किया जाता है। जांच किए गए एल्गोरिदम को मॉडल डेटा पर लागू करते हुए, हम पहले से अनुमान लगा सकते हैं कि इसके निष्पादन का परिणाम क्या होगा। यदि यह संतोषजनक हो जाता है, तो आप इसे वास्तविक डेटा पर लागू करने का प्रयास कर सकते हैं। स्वाभाविक रूप से, यह केवल nonparametric एल्गोरिथम पर लागू होता है, अर्थात, डेटा वितरण के कानून से स्वतंत्र।

सबसे अधिक इस्तेमाल किया जाने वाला मॉडलिंग डेटा सामान्य कानून के अनुसार वितरित किया जाता है। दुर्भाग्य से, एमएस एक्सेल और आम सांख्यिकीय पैकेज (एसपीएसएस, स्टेटिस्टिका) मॉडलिंग को केवल एक आयामी सांख्यिकीय वितरण की अनुमति देते हैं। बेशक, एक बहुआयामी वितरण कई एक आयामी लोगों से बना हो सकता है, लेकिन केवल अगर चर स्वतंत्र हैं। यदि आपको एक दूसरे के आधार पर चर के साथ डेटा की जांच करने की आवश्यकता है, तो आपको एक कार्यक्रम लिखना होगा।

आमतौर पर संकेत मिलता है कि बहुआयामी सामान्य वितरण

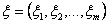
गणितीय अपेक्षाओं के एक वेक्टर द्वारा वर्णित है

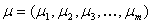
और सकारात्मक निश्चित सहसंयोजक मैट्रिक्स

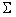
जहाँ

;
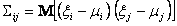
i = 1,2,3, ... m, j = 1,2,3, ..., m;
मीटर एक बहुआयामी सामान्य नमूने की सुविधाओं की संख्या है।

हालांकि, सहसंयोजक मैट्रिक्स के बजाय, सहसंबंध मैट्रिक्स का उपयोग करना अधिक सुविधाजनक है

और फैलाव वेक्टर

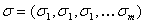
, सहसंबंध गुणांक, सहसंयोजक गुणांक के विपरीत, चर के बीच संबंध की डिग्री को दर्शाता है। सहसंबंध मैट्रिक्स का रूप है:

मैट्रिक्स गुणांक का रूपांतरण

मैट्रिक्स गुणांक के लिए

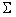
सूत्र के अनुसार होता है:

एक वेक्टर मॉडल करने के लिए

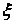
आप रैखिक वेक्टर परिवर्तन का उपयोग कर सकते हैं

जिनके घटक सामान्य रूप से शून्य और फैलाव के बराबर गणितीय अपेक्षा मापदंडों के साथ यादृच्छिक चर वितरित किए जाते हैं (अर्थात।

)। एक आयामी सामान्य यादृच्छिक चर को मॉडल करने के कई तरीके हैं, उदाहरण के लिए, बॉक्स-मुलर रूपांतरण: दो यादृच्छिक संख्याओं का उपयोग करना

और

अंतराल पर वितरित (0; 1), जिस पर दो नंबर एक साथ प्राप्त होते हैं, मापदंडों के साथ सामान्य कानून के अनुसार वितरित किए जाते हैं

परिवर्तन

में

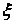
सूत्र द्वारा निर्मित:

इस परिवर्तन में

मैट्रिक्स से एक कम त्रिकोणीय मैट्रिक्स है

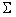
चोल्स्की अपघटन

प्रत्येक मैट्रिक्स तत्व

एक पुनरावर्ती प्रक्रिया का उपयोग करके निर्धारित:

जहां सूचकांक सीमा में भिन्न होते हैं

, और ऊपरी शून्य चैपल के साथ रकम शून्य के बराबर है (अर्थात, यदि

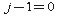
तो

।

)।

वर्णित परिवर्तन को C ++ में दो फ़ंक्शन के रूप में लागू किया जा सकता है: मुख्य फ़ंक्शन normal_model () जो एल्गोरिथ्म को लागू करता है और सहायक मैट्रिक्स_डेटमेटिन () जो मैट्रिक्स के निर्धारक को लौटाता है।

Normal_model () फ़ंक्शन परिणाम के साथ मैट्रिक्स के आयाम से आवश्यक चर और मूल्यों की संख्या निर्धारित करता है। सफलता के मामले में, असफलता के मामले में, सच है - झूठ।

//   ,    . //double MatrixMath [mq] -  .  //double MatrixDisp [mq] -   //vector<vector<double> > &correlation_matrix -   //vector<vector<double> > &MatrixRes -    bool normal_model (double MatrixMath[], double MatrixVar[], vector<vector<double> > &correlation_matrix, vector<vector<double> > &MatrixRes){ int mq =MatrixRes[0].size();//  int count=MatrixRes.size();//  double MatrixA[mq][mq]; //   A double MatrixN[count][mq]; //  ,       0, 1 int i,j,k; double suma, sumaa; double alfa1, alfa2; //.  ,    (0;1] vector<vector<double> > MatrixK(mq); //  K for (i=0;i<mq;i++){ MatrixK[i].resize(mq); } //     for (i=0; i<mq; i++){ for (j=0; j<mq; j++){ MatrixK[i][j]= correlation_matrix[i][j]* sqrt(MatrixVar[i]*MatrixVar[j]); } } if (matrix_determinant(MatrixK)<=0) return false; // .      ; //  A for (i=0; i<mq; i++){ for (j=0; j<=i; j++){ sumA=0; sumAA=0; for (k=0; k<j; k++){ sumA+= MatrixA[i][k] * MatrixA[j][k]; sumAA+= MatrixA[j][k] * MatrixA[j][k]; } MatrixA[i][j]=(MatrixK[i][j] - sumA)/ sqrt(MatrixK[j][j] - sumAA); } } //  ,       0, 1 srand(time(NULL)); for (i=0; i<count; i+=2){ for (j=0; j<mq; j++){ alfa1 = (double)rand()/(RAND_MAX+1.0); alfa2 = (double)rand()/(RAND_MAX+1.0); if (!alfa1 || !alfa2){ j--; }else{ MatrixN[i][j] = sqrt(-2*log(alfa1))*sin(2*M_PI*alfa2); if (i+1<count) MatrixN[i+1][j] = sqrt(-2*log(alfa1))*cos(2*M_PI*alfa2); } } } //   ,       0, 1      for (i=0; i<count; i++){ for (j=0; j<mq; j++){ MatrixRes[i][j]=MatrixMath[j]; for (k=0; k<mq; k++){ MatrixRes[i][j]+=MatrixA[j][k] * MatrixN[i][k]; } } } return true; } //    m  N x N double matrix_determinant (vector<vector<double> > & m){ double result=0; if (m.size()==1){ return m[0][0]; }else if(m.size()==2){ return m[0][0] * m[1][1] - m[0][1] * m[1][0]; }else if(m.size()==3){ return m[0][0] * m[1][1] * m[2][2] + m[0][1] * m[1][2] * m[2][0] + m[0][2] * m[1][0] * m[2][1] - m[2][0] * m[1][1] * m[0][2] - m[1][0] * m[0][1] * m[2][2] - m[0][0] * m[2][1] * m[1][2]; }else{ vector<vector<double> > m1(m.size()-1);// N-1 x N-1,     N-1 for (int i=0; i<m.size()-1; i++){ m1[i].resize(m.size()-1); } for (int i=0; i< m.size(); i++){ for (int j=1; j<m.size(); j++){ for (int k=0; k<m.size(); k++){ if (k<i){ m1[j-1][k] = m[j][k]; }else if(k>i){ m1[j-1][k-1] = m[j][k]; } } } result+= pow(-1,i) *m[0][i] * matrix_determinant(m1); } } return result; }

काम का परिणाम यहां पाया जा सकता है । फ़ंक्शन को फास्टकगी तंत्र के माध्यम से एक्सेस किया जाता है।

प्रयुक्त साहित्य:

मार्टीशेंको सी। एन।, मार्टिश्नो एन.एस., कुस्तोव डी.ए. बहुआयामी डेटा मॉडलिंग और कंप्यूटर प्रयोग। इंजीनियरिंग और प्रौद्योगिकी, 2007. - नंबर 2। एस। 47-52।
एर्मकोव एस.एम., मिखाइलोव जी.ए., सांख्यिकीय मॉडलिंग), मॉस्को: नाका, 1982।
वी। फेलर, प्रोबेबिलिटी थ्योरी का परिचय और इसके अनुप्रयोग, ट्रांस। अंग्रेजी से।, टी। 1-2, एम।, 1964-67।
रेनचर, एल्विन सी। (2002), मेथड्स ऑफ मल्टीवेरेट एनालिसिस, सेकंड एडिशन, जॉन विली एंड संस।

सामान्य कानून के अनुसार वितरित एक बहुआयामी डेटा सरणी मॉडलिंग के लिए एल्गोरिदम

More articles: