Nonlinear गतिशीलता और समय श्रृंखला विश्लेषण - पुनरावृत्ति भूखंड विधि की समीक्षा

सभी को नमस्कार। इस विषय में, मैं नॉनलाइनियर डायनामिक्स की एक अपेक्षाकृत नई और बल्कि शक्तिशाली विधि की समीक्षा करना चाहता हूं - समय श्रृंखला के विश्लेषण के लिए पुनरावृत्ति भूखंड विधि या आवेदन में पुनरावृत्ति विश्लेषण। और, इसके अलावा, वह मतलाब भाषा में एक छोटे कार्यक्रम का कोड साझा करेगा, जो नीचे वर्णित सब कुछ को लागू करता है।

तो चलिए शुरू करते हैं। ड्यूटी पर, मैं गैर-रेखीय गतिशीलता, वीडियो और छवि प्रसंस्करण से निपटता हूं, मैं यहां तक ​​कि गैर-रैखिक गतिशीलता के गैर-रैखिक हिस्से - रोटार के गैर-रैखिक दोलन कहूंगा। जैसा कि आप जानते हैं, एक कंपन संकेत समय श्रृंखला से अधिक कुछ नहीं है, जहां संकेत विचलन के आयाम का मूल्य है, ठीक है, उदाहरण के लिए, एक हवाई जहाज टरबाइन का रोटर। जैसा कि आप जानते हैं, इस रूप में न केवल रोटर कंपन का प्रतिनिधित्व किया जा सकता है। स्टॉक कोट्स में उतार-चढ़ाव, सूरज की गतिविधि और कई अन्य प्रक्रियाओं को समय में व्यवस्थित संख्याओं के एक साधारण वेक्टर द्वारा वर्णित किया जाता है। मैं और भी अधिक कहूंगा कि ये सभी प्रक्रियाएं एक महत्वपूर्ण कारक से एकजुट होती हैं - वे अरेखीय हैं, और कुछ अराजक भी हैं, जिसका अर्थ है कि अंतर-समीकरणों के रूप में अपनी गति के नियम को जानते हुए भी समय की एक बड़ी अवधि के लिए सिस्टम में राज्य की भविष्यवाणी करने में असमर्थता। और सबसे महत्वपूर्ण बात यह है कि ज्यादातर मामलों में हम किसी भी रूप में ये बहुत समीकरण नहीं लिख सकते हैं। और यहाँ प्रयोग और nonlinear गतिशीलता बचाव के लिए आते हैं।

नॉनलाइनर डायनेमिक्स

सेंसर से रीडिंग लेना (मुद्राओं के उद्धरण के साथ एक फ़ाइल डाउनलोड करना), हमारे पास एक-आयामी संकेत है, आमतौर पर आउटपुट में जटिल आकार। यदि संकेत आवधिक है तो यह अच्छा है। और अगर नहीं? अन्यथा, हम एक जटिल प्रणाली के साथ काम कर रहे हैं, जो, इसके अलावा, nonlinear और अराजक दोलनों के मोड में हो सकता है। इस मामले में, एक जटिल प्रणाली का मतलब है कि बड़ी संख्या में स्वतंत्रता के साथ एक प्रणाली का मतलब है। लेकिन हमें सेंसर से एक-आयामी संकेत मिलता है। इस प्रणाली की स्वतंत्रता की अन्य डिग्री के बारे में कैसे जानें?

इससे पहले कि हम मुख्य बिंदु पर आगे बढ़ें, यह नॉनलाइनियर डायनामिक्स का विश्लेषण करने के लिए एक और शक्तिशाली विधि का उल्लेख करने योग्य है, जो समय श्रृंखला के विश्लेषण के तरीकों पर आसानी से चले गए। यह स्वतंत्रता के केवल एक डिग्री से एक संकेत द्वारा सिस्टम प्रक्षेपवक्र की तथाकथित बहाली है। उदाहरण के लिए, एक गेंद एक धागे के चारों ओर एक चक्र में घूमती है, और यदि हम एक विमान में इस प्रक्रिया को देखते हैं, तो हम केवल एक अक्ष से एक संकेत को शूट कर सकते हैं, हमारे लिए गेंद आगे और पीछे चलेगी। और अब, यह पता चला है कि आप पूरी प्रणाली के एन-आयामी संकेत को पूरी तरह से बहाल कर सकते हैं। लेकिन पूर्ण में नहीं, बल्कि केवल सिस्टम के सामयिक गुणों के संरक्षण के साथ (दूसरे शब्दों में, इसकी ज्यामिति)। इस मामले में, यदि गेंद आवधिक प्रक्षेपवक्र के साथ चलती है, तो बहाल प्रक्षेपवक्र आवधिक होगा। विधि स्वयं एक सरल सूत्र पर आधारित है (द्वि-आयामी प्रणाली के मामले में):

Y (i) = X (t), Y1 (i) = X (t + n), जहां n समय की देरी है, और Y, Y1 पहले से बहाल संकेत है। टेकेन्स प्रमेय में यह साबित हुआ है। उदाहरण में, अंतरिक्ष द्वि-आयामी है, लेकिन वास्तव में यह एक मनमाने ढंग से बड़ी संख्या में आयामों का स्थान हो सकता है। अंतरिक्ष के आयाम का अनुमान लगाने की विधि इस विषय के विषय में शामिल नहीं है, मैं केवल उल्लेख करता हूं कि यह हो सकता है, उदाहरण के लिए, झूठे पड़ोसियों की विधि।

पुनरावृत्ति भूखंड विधि

तो, हमें उस प्रणाली का प्रक्षेपवक्र मिला जिसमें वास्तविक भौतिक प्रणाली के सामयिक गुणों को संग्रहीत किया जाता है, जो बहुत महत्वपूर्ण है। अब हम पैटर्न की पहचान करने के लिए उस पर छवि मान्यता विधियों का एक पूरा शस्त्रागार सेट कर सकते हैं। लेकिन उनमें से सभी, एक तरह से या किसी अन्य, की अपनी कंप्यूटिंग खामियां हैं या उन्हें लागू करना मुश्किल है। और 1987 में, एकमैन और सहकर्मियों ने एक नई विधि विकसित की, जिसका सार निम्नलिखित को उबालता है। ऊपर प्राप्त प्रक्षेपवक्र, जो कि आयाम N के वैक्टर का एक समूह है, को सूत्र का उपयोग करके दो-आयामी विमान पर मैप किया गया है:

R [i, j, m, e] = O (e [i], - || S [i] - S [j] ||), जहां i, j समतल पर एक बिंदु के सूचक हैं, m, एम्बेडिंग स्पेस का आयाम है, || ओ - हीविसाइड फंक्शन ||… || - आदर्श या दूरी (उदाहरण के लिए, यूक्लिडियन)। परिणामी और विज़ुअलाइज्ड मैट्रिक्स की उपस्थिति हमें सिस्टम की गतिशीलता का विचार देगी, जो मूल रूप से एक समय श्रृंखला के रूप में प्रस्तुत की जाती है। हम वुल्फ संख्याओं के साथ प्रयोग के रूप में उपरोक्त सभी का वर्णन करते हैं, जो सूर्य की गतिविधि का वर्णन करते हैं (इस श्रृंखला के बजाय, आप आसानी से मुद्रा उद्धरण ले सकते हैं)।

परिणाम

यह संकेत ही है:



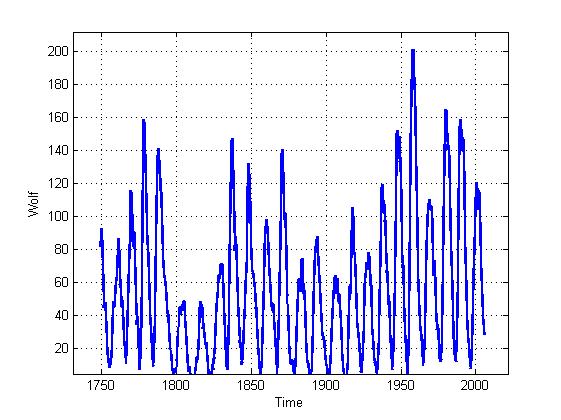
यह दो आयामी अंतरिक्ष में एक बहाल प्रक्षेपवक्र है (हम सादगी के लिए दो आयामी स्थान लेते हैं, हालांकि वास्तव में इसमें बड़ी संख्या में आयाम हैं, लेकिन जैसा कि अभ्यास से पता चलता है, यह गुणात्मक मूल्यांकन के लिए काफी पर्याप्त है)



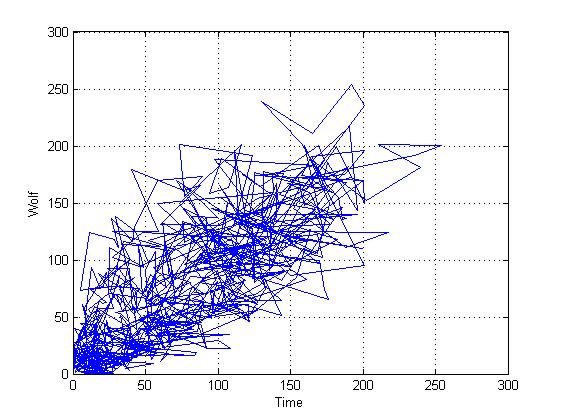
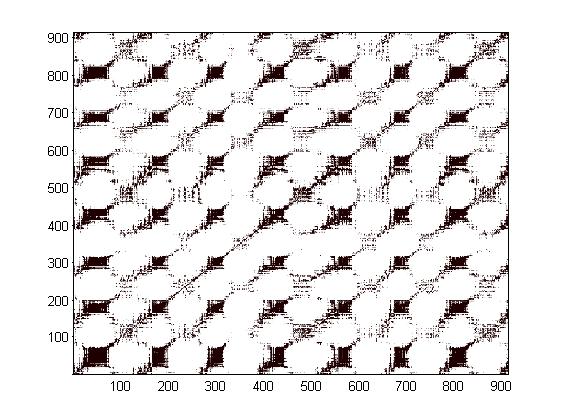
यह तथाकथित दूरी मैट्रिक्स है (आई-वें बिंदु से जम्मू-वें बिंदु तक की दूरी के अर्थ में)। अक्सर इन आरेखों में एक जटिल डिज़ाइन होता है जिसे डिज़ाइन में उपयोग (और उपयोग) किया जा सकता है।



ठीक है, वास्तव में पुनरावर्ती आरेख। विश्लेषण के सभी तरीकों का वर्णन करने के लिए, ऐसा आरेख पर्याप्त नहीं है और 400 पृष्ठ हैं। गुणात्मक विश्लेषण के अलावा, यह विधि मात्रात्मक संकेतकों को भी अनुमति देती है, जिसका उपयोग तंत्रिका नेटवर्क के मामले में सफलतापूर्वक किया जा सकता है। लेकिन सबसे महत्वपूर्ण बात यह है कि पहले से ही इस चित्र पर एक त्वरित नज़र डाली जा रही है, हम इसके बारे में बहुत कुछ कह सकते हैं। सबसे पहले, मुख्य विकर्ण के लंबवत बैंड की उपस्थिति प्रणाली में अराजक या स्टोकेस्टिक प्रक्रियाओं की उपस्थिति को इंगित करती है (बिल्कुल कहने के लिए, अतिरिक्त अध्ययन की आवश्यकता होती है)। काले डॉट्स के साथ असमान रूप से भरे हुए क्षेत्रों की उपस्थिति अस्थिर प्रक्रियाओं को इंगित करती है और आपको समय में इन प्रक्रियाओं की सीमाओं को सटीक रूप से निर्धारित करने की अनुमति देती है।

मतलाब कोड

clear; clc;
%
[X1,X2,X3,X4]=textread('data.txt','%f %f %f %f');
plot(X2,X4);grid;hold; ; ylabel('Wolf');xlabel('Time');
N = length(X1);
M = round(0.3*N);
M1 = N - M;
m = 2; %
t = 10; %
%
X(1,1) = 0;
X(1,2) = 0
j = 1;
%
for i=M1:(N - t)
X(j,1) = X3(i);
X(j,2) = X3(i + t);
j = j + 1;
end
figure;
plot(X(:,1),X(:,2));grid;hold; ; ylabel('Wolf');xlabel('Time');
N1 = length(X(:,1))
D1(1,1) = 0;
D2(1,1) = 0;
e = 30;
% RP -
for i = 1:N1
for j = 1:N1
D1(i,j)=sqrt((X(i,1)-X(j,1))^2+(X(i,2)-X(j,2))^2);
if D1(i,j) < e
D2(i,j) = 0;
else
D2(i,j) = 1;
end;
end;
end;
figure;
pcolor(D2) ;
shading interp;
colormap(pink);
figure;
pcolor(D1) ;
shading interp;
colormap(pink);
hold on

पुनश्च। यह सिर्फ एक प्राथमिक उदाहरण है, जो निश्चित रूप से, इस पद्धति की पूरी शक्ति को कवर नहीं करता है। सरलतम मामले में, प्रक्रिया को स्वचालित करने के लिए, आप विमान पर आंकड़े खोजने के लिए एल्गोरिदम का उपयोग कर सकते हैं। ऐसे सिस्टम विमान टरबाइन मॉनिटरिंग सिस्टम में प्रासंगिक हो सकते हैं, साथ ही विभिन्न वित्तीय प्रक्रियाओं के लिए मॉनिटरिंग सिस्टम भी हो सकते हैं। मैंने इस विषय के सबसे दिलचस्प हिस्से को नहीं छुआ - इन आरेखों के मात्रात्मक संकेतकों की गणना, जिसे मैं अगले विषयों में क्षतिपूर्ति करने की कोशिश करूंगा।

साहित्य

• जे.-पी. एकमान एन एस ऑलिफसन काम्फोर्स्ट और डी। रूएल, डायनामिकल सिस्टम्स के पुनरावृत्ति भूखंड
• www.recurrence-plot.tk
• en.wikipedia.org/wiki/Recurrence_plot