🤦 🌼 👡 نسيج الكم الزمكان: شبكة نسيج ❓ 🚵🏿 😚

كيف أزواج الكم غرزة الزمكان

الجزء الأول ، درس

براين سوينغل الفيزياء في كلية الدراسات العليا بمعهد ماساتشوستس للتكنولوجيا ، عندما قرر أن يأخذ فصلين في نظرية الأوتار لتحسين تعليمه - كما يتذكر ، على مبدأ "لماذا لا" - على الرغم من أنه لم يهتم في البداية بالمفاهيم الذي التقى به في هذه الدورة. ولكن غرق أعمق ، بدأ يلاحظ اتصالات غير متوقعة مع عمله الخاص ، حيث استخدم ما يسمى ب شبكات الموتر للتنبؤ بخصائص المواد الغريبة ونهج فيزياء الثقب الأسود والجاذبية الكمية ، مأخوذة من نظرية الأوتار. يقول: "أدركت أن شيئًا رائعًا يحدث".

ينشأ الموترون بشكل دوري بشكل غير متوقع في مجالات مختلفة من الفيزياء - وهي أشياء رياضية يمكن أن تمثل العديد من الأرقام في وقت واحد. على سبيل المثال ، ناقل السرعة هو أبسط موتر: فهو يتضمن كل من السرعة والاتجاه. يمكن استخدام الموترات الأكثر تعقيدًا المتصلة بالشبكة لتبسيط الحسابات للأنظمة المعقدة المكونة من العديد من الأجزاء المتفاعلة - بما في ذلك التفاعلات المعقدة لعدد كبير من الجسيمات دون الذرية التي تشكل المادة.

Swing هو واحد من عدد متزايد من الفيزيائيين الذين يرون قيمة تطبيق شبكات الموتر على علم الكونيات. من بين الفوائد الأخرى ، يمكن أن يساعد هذا في حل النقاش الجاري حول جوهر الزمكان. جون بريسكيليعتقد البروفيسور ريتشارد فاينمان من الفيزياء النظرية في KalTech أن العديد من الفيزيائيين اشتبهوا في وجود علاقة عميقة بين التشابك الكمي - العمل المخيف طويل المدى الذي جعل أينشتاين غاضبًا جدًا - وهندسة الزمكان على أصغر المقاييس. استمر هذا الأمر منذ أن وصف جون ويلر ، قبل ستين عامًا ، الزمان لأول مرة بأنه رغوة فقاعية. يقول بريسكيل: "إذا كنت تدرس الهندسة بمقاييس مماثلة لمقاييس بلانك" - في أقصر مسافة ممكنة - "فإنها تبدو أقل وأقل تشبه الزمكان". "هذه ليست هندسة على الإطلاق ، ولكن شيء آخر ، شيء ينشأ من أشياء أساسية أكثر."

يواصل الفيزيائيون النضال مع المشكلة المربكة لما قد تكون هذه المشكلة الأساسية ، لكنهم يشكون في أنها مرتبطة بالمعلومات الكمومية. يقول بريسكيل: "عندما نتحدث عن معلومات الترميز ، نعني أنه يمكنك تقسيم النظام إلى أجزاء وسيكون هناك مثل هذا الارتباط بينهما بحيث يمكنني أن أتعلم شيئًا عن أحد الأجزاء ، أشاهد الآخر". هذا هو جوهر الخلط.

غالبًا ما يتحدثون عن "نسيج" الزمكان ، وتؤدي هذه الاستعارة إلى مفهوم خياطة الخيوط الفردية معًا لتشكيل كل سلسة. هذه الخيوط هي في الأساس كمية. يقول سوينغل ، الذي يعمل حاليًا على البحث في جامعة ستانفورد: "إن التشابك هو نسيج الزمكان". - هذا هو الخيط الذي يربط النظام بأكمله معًا ، مما يضمن الفرق بين الخصائص العامة وخصائص الكيانات الفردية. ولكن من أجل رؤية السلوك التعاوني المثير للاهتمام ، عليك أن تفهم كيف يتم توزيع التشابك ".

توفر شبكات Tensor أداة رياضية يمكنها القيام بذلك. من وجهة النظر هذه ، ينشأ الزمكان من مجموعات من العقد لشبكة معقدة متصلة ببعضها البعضحيث تتناسب قطع صغيرة من المعلومات الكمية معًا مثل Lego. التشابك هو الغراء الذي يربط الشبكة. لفهم الزمكان ، من الضروري أولاً النظر في التشابك من المواضع الهندسية ، لأن هذه هي الطريقة التي يتم بها ترميز المعلومات في عدد كبير من عقد النظام المتفاعل.

العديد من الهيئات ، شبكة واحدة

إن نمذجة نظام كمومي معقد ليست مزحة. حتى النظام الكلاسيكي الذي يحتوي على أكثر من جزأين متفاعلين معقد تمامًا للنمذجة. عندما نشر إسحاق نيوتن كتابه Principia [المبادئ الرياضية للفلسفة الطبيعية] في عام 1687 ، كان أحد مواضيع الكتاب هو "مشكلة الأجسام الثلاثة". إن مهمة حساب حركة جسمين ، على سبيل المثال ، الشمس والأرض ، مع الأخذ في الاعتبار انجذابهما المتبادل ، بسيطة نسبيًا. ولكن إذا قمت بإضافة جسم ثالث إليه - على سبيل المثال ، القمر - فإنه يتحول من مهمة بسيطة مع حل دقيق إلى فوضوي ، حيث تتطلب التنبؤات طويلة المدى أنظمة حوسبة قوية لمحاكاة التطور التقريبي للنظام. وكلما زاد عدد الكائنات في النظام ، زادت الحسابات تعقيدًا ، وزاد تعقيدها بشكل خطي تقريبًا - على الأقل في الفيزياء الكلاسيكية.

تخيل الآن نظامًا كميًا بمليارات الذرات ، يتفاعل كل منها مع الآخرين وفقًا للمعادلات الكمية المعقدة. على هذا المقياس ، يبدو أن التعقيد ينمو بشكل كبير مع عدد الجسيمات في النظام ، لذلك لن ينجح نهج القوة الغاشمة في الحوسبة.

تخيل الكتلة الذهبية. وتتكون من مليارات الذرات ، وتتفاعل جميعها مع بعضها البعض. من هذه التفاعلات ، تتبع الخصائص الكلاسيكية المختلفة للمعدن - اللون أو القوة أو الموصلية. يقول سوينغل: "الذرات هي أشياء صغيرة جدًا تطيع ميكانيكا الكم ، وعندما تضعها معًا ، تحدث أشياء جديدة ومذهلة". ولكن على هذا النطاق ، تبدأ قواعد ميكانيكا الكم في العمل. يحتاج الفيزيائيون لحساب الدالة الموجية لهذه الكتلة بدقة ، والتي تصف حالة النظام. وهذه الوظيفة هيدرا متعددة الرؤوس من التعقيد الأسي.

حتى لو لم يكن هناك سوى مئة ذرة في الكتلة وكان لكل منها دوران كمّي يأخذ إحدى حالتين ، لأعلى أو لأسفل ، فإن العدد الإجمالي للحالات المحتملة سيكون بالفعل ^2،100مليون تريليون تريليون. ومع إضافة كل ذرة ، تزداد المهمة سوءًا بشكل كبير. (ويزداد الأمر سوءًا عندما تحاول وصف شيء آخر غير الدوران ، كما يجب أن يفعل أي نموذج واقعي). يقول سوينجل: "إذا أخذت الكون المرئي بالكامل وقمت بملئه بأفضل محركات الأقراص المتاحة ، وأفضل محركات الأقراص الثابتة ، يمكنك تخزين 300 دورة فقط عليها". - هناك معلومات ، لكنها لا تتوافق جميعها مع الفيزياء. لم يسبق لأحد أن قاس هذه الأرقام ".

تسمح شبكات Tensor للفيزيائيين بضغط جميع المعلومات الموجودة في دالة الموجة والتركيز فقط على تلك الخصائص التي يمكن قياسها تجريبيًا: مدى قوة المادة التي تنكسر الضوء ، أو مدى امتصاصها للصوت ، أو كيفية توصيلها بالكهرباء. الموتر هو صندوق أسود يأخذ مجموعة من الأرقام ويعطي مجموعة أخرى. لذلك ، يمكنك توصيل دالة موجية بسيطة - على سبيل المثال ، العديد من الإلكترونات التي لا تتفاعل مع بعضها البعض في حالة بأقل طاقة - ومعالجتها مع الموترين مرارًا وتكرارًا حتى تنتج العملية دالة موجية لنظام كبير ومعقد ، مثل تفاعل المليارات في الكتلة الذهبية للذرات. والنتيجة هي رسم تخطيطي بسيط يمثل هذه الكتلة المعقدة - الابتكار ،قابلة للمقارنة مع المخططات التي طورها Feynman في منتصف القرن العشرين والتي بسطت تمثيل تفاعلات الجسيمات. وشبكة الموتر لها هندستها الخاصة ، وكذلك الزمكان.

يكمن مفتاح التبسيط في مبدأ "المحلية". يتفاعل كل إلكترون فردي فقط مع أقرب الإلكترونات. إن تشابك كل إلكترون مع جيرانه يعطي مجموعة من "عقد" الشبكة. هذه العقد عبارة عن موترات وتشابك بينهما. كل هذه العقد المترابطة تشكل الشبكة. تصبح الحسابات المعقدة أسهل للتصور. في بعض الأحيان يتعلق الأمر بمهمة حساب أبسط.

هناك العديد من الأنواع المختلفة لشبكات الموتر ، ولكن من بين الأكثر فائدة هناك واحد معروف بالاختصار MERA (anzats renormalization of multiscale clangment). مبدأ عملها كما يلي: تخيل خطًا واحدًا من الإلكترونات. استبدل ثمانية إلكترونات مختلفة - تشير إليها بواسطة A و B و C و D و E و F و G و H - بالوحدات الأساسية للمعلومات الكمية (qubits) وتشابك كل منها مع جار لتشكيل روابط. يتم الخلط بين A و B و C مع D وما إلى ذلك. ينتج عن هذا شبكة ذات مستوى أعلى. ثم قم بخلط AB مع CD و EF مع GH للانتقال إلى طبقة أخرى من الشبكة. وأخيرًا ، يتم الخلط بين ABCD و EFGH لتشكيل أعلى مستوى. كتب رومان أوروس في عمله في العام الماضي: "يمكننا القول ، إلى حد ما ، أن التشابك يُستخدم لبناء الوظيفة الموجية لكثير من الأجساد".Román Orús ] ، فيزيائي من الجامعة. يوهانس جوتنبرج (ألمانيا).

لماذا يعتبر بعض الفيزيائيين متفائلين للغاية بشأن إمكانات شبكات الموتر - خاصة MERA - التي يمكن أن تقودهم إلى الجاذبية الكمية؟ لأن الشبكات تُظهر كيف يمكن أن تنشأ بنية هندسية بسيطة من التفاعلات المعقدة بين العديد من الكائنات. وتأمل Swingle مع أشخاص متشابهين في التفكير أن تكون هذه الهندسة الجديدة قابلة للاستخدام ، مما يوضح كيف تشرح الآلية التي يتم من خلالها تحويل الأجزاء الفردية من المعلومات الكمية إلى زمان سلس ومستمر.

حدود الزمكان

عند تطوير شبكات الموتر ، اكتشف خبراء في فيزياء المادة المكثفة عن طريق الخطأ بُعدًا إضافيًا: تؤدي هذه التقنية إلى ظهور أنظمة ثنائية الأبعاد في بُعد واحد. وأزال خبراء في نظرية الجاذبية بعدًا واحدًا - الانتقال من ثلاثة إلى اثنين - تطوير ما يسمى مبدأ التصوير المجسم. يمكن أن يجتمع هذان المفهومان معًا ويخلقان رؤية أكثر تعقيدًا للزمكان.

في سبعينيات القرن الماضي ، أظهر الفيزيائي جاكوب بيكنشتاين أن المعلومات حول الثقب الأسود من الداخل مشفرة على سطحه الثنائي الأبعاد المسطح (على الحدود) ، وليس في حجمه ثلاثي الأبعاد. بعد عشرين عامًا ، قام ليونارد ساسكيند وجيرارد تي هوفت [ليونارد ساسكيند وجيرارد تي هوفت] بتوسيع هذا المفهوم ليشمل الكون بأكمله ، معادلًا ذلك إلى صورة ثلاثية الأبعاد: ينشأ كوننا ثلاثي الأبعاد بكل روعته من "شفرة مصدر ثنائية الأبعاد". في عام 1997 ، وجد خوان مالداسينا مثالًا ملموسًا على عمل صورة ثلاثية الأبعاد ، مما يدل على أن نموذج اللعبة لوصف المساحة المسطحة دون الجاذبية يعادل وصف مساحة على شكل سرج مع الجاذبية. هذه العلاقة بين الفيزياء تسمى "الازدواجية".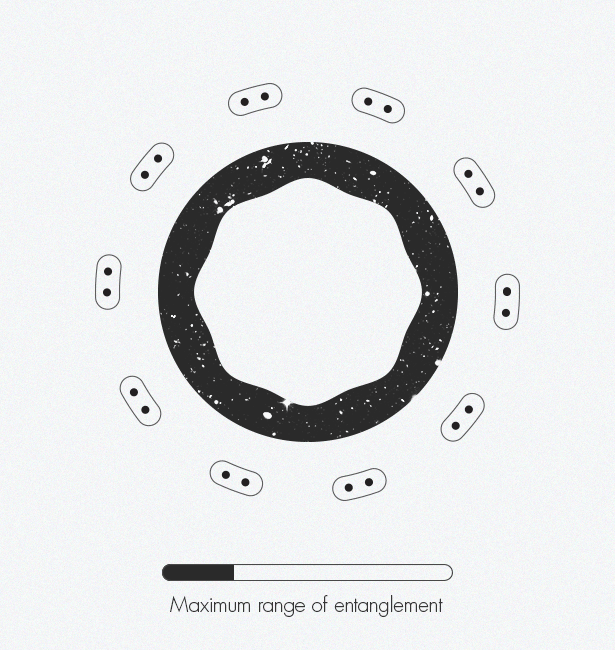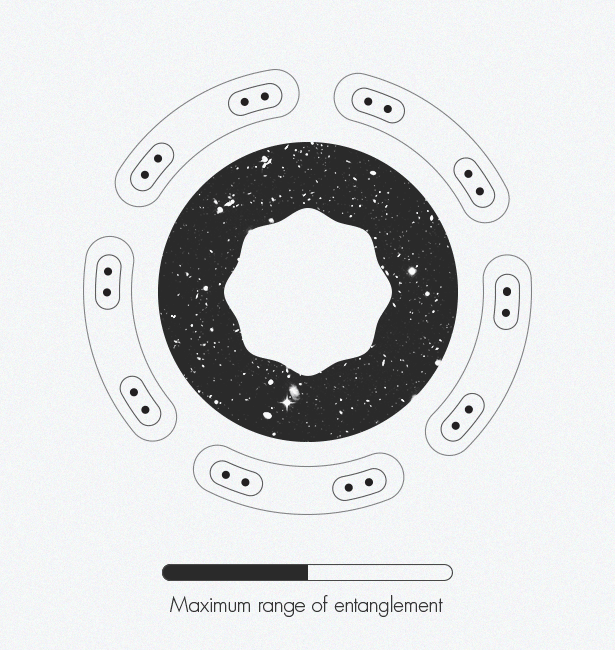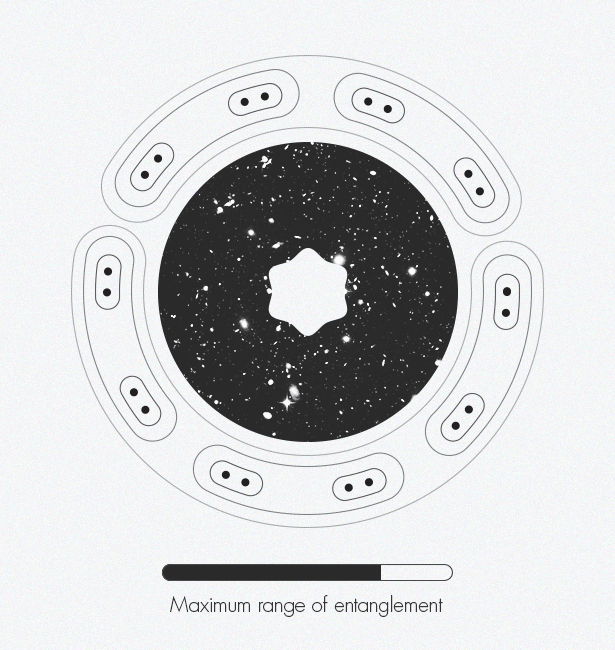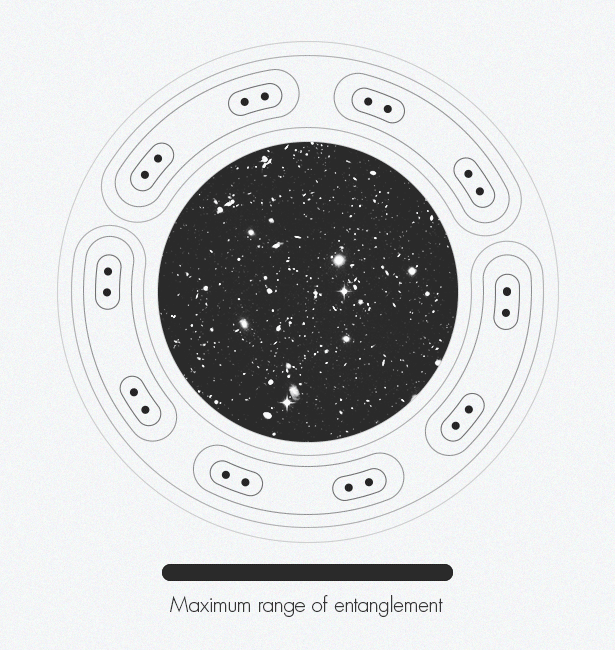

مارك فان رامسدونك [ مارك فان رامسدونك] يمثل كيف يؤدي التشابك تدريجياً إلى الزمكان. على طول حواف الشكل ، تبدأ جزيئات النقاط الفردية في التشابك مع بعضها البعض. تتشابك هذه الأزواج المتشابكة مع أزواج أخرى. مع تزايد تشابك الأزواج ، تظهر بنية الزمكان.

يقارن مارك فان رامسدونك ، أخصائي نظرية الأوتار في جامعة كولومبيا البريطانية (فانكوفر) ، هذا المبدأ المجسم بشريحة كمبيوتر ثنائية الأبعاد تحتوي على كود لإنشاء عالم افتراضي ثلاثي الأبعاد في لعبة الكمبيوتر. نحن نعيش داخل الفضاء ثلاثي الأبعاد للعبة. بمعنى ما ، فضاءنا وهمي وهو فقط صورة سريعة الزوال معلقة في الهواء. لكن فان رامسدونك يؤكد أنه "لا يزال هناك نوع من الكيان المادي في الكمبيوتر الذي يخزن جميع المعلومات".

تم قبول الفكرة على نطاق واسع بين الفيزيائيين النظريين ، لكنهم لا يزالون يعانون من كيفية تخزين الأبعاد الأصغر للمعلومات حول الهندسة الزمانية. المصيد هو أن رقاقة الكمبيوتر المجازية الخاصة بنا يجب أن تكون نوعًا ما من أجهزة الكمبيوتر الكمومية ، حيث يتم استبدال الأصفار المعتادة والأخرى بالكيلوبتات ، القادرة على تمثيل جميع الحالات المحتملة في وقت واحد من صفر إلى واحد. يجب أن تكون هذه الكيوبتات متشابكة - بحيث يتم تحديد حالة كيوبت واحدة من قبل دولة جارتها - قبل أن يتم تشفير عالم واقعي ثلاثي الأبعاد.

وبالمثل ، يبدو أن التشابك سمة أساسية في الزمكان. توصل عالمان إلى هذا الاستنتاج في عام 2006: Shinsei Ryu [جامعة إلينوي] و Tadashi Takayanagi (جامعة كيوتو) الذين تقاسموا جائزة New Horizons of Physics في عام 2015. يوضح Van Raamsdonk أن "الفكرة هي أن طريقة تشفير هندسة الزمكان ترتبط ارتباطًا وثيقًا بكيفية تشابك أجزاء مختلفة من هذه الشريحة مع بعضها البعض".

مستوحى من عملهم ، وكذلك عمل مالداسينا الذي أعقب ذلك ، في عام 2010 ، اقترح فان راامسدونك تجربة فكرية تظهر الدور الحاسم للتشابك في تكوين الزمكان. بحث في ما سيحدث إذا قسمت شريحة الكمبيوتر إلى النصف ، ثم أزل التشابك بين الكوبت في النصفين. وجد أن الزمكان يبدأ في الانهيار بنفس الطريقة التي يؤدي بها تمديد قطعة من العلكة من نهاياتها إلى فجوة في الوسط. يقسم تقسيم هذه الشريحة إلى قطع أصغر وأصغر مساحة الوقت حتى تبقى فقط قطع منفصلة وغير متصلة. يقول فان راامسدونك: "إذا أزلت الارتباك ، فسوف ينهار الزمكان". وبالمثل ، "إذا كنت ترغب في بناء الزمكان ،عليك الخلط بين الكوبتات بطريقة معينة ".

اجمع بين هذه الأفكار وعمل Swingle ، وربط البنية الزمانية المعقدة والمبدأ الهولوغرافي بشبكات الموتر وقطعة أخرى من اللغز تناسبها في مكانها. ينشأ الزمكان المنحني بشكل طبيعي من التشابك في شبكات الموتر من خلال التصوير المجسم. يقول فان راامسدونك: "الزمكان هو التمثيل الهندسي لهذه المعلومات الكمية".

وكيف تبدو هذه الهندسة؟ في حالة الزمكان على شكل سرج في Maldasena ، يبدو وكأنه أحد الرسوم "الحد - الدائرة" التي رسمها Escher من 1950-1960. لطالما اهتم إيشر بالترتيب والتناظر ، بما في ذلك هذه المفاهيم الرياضية في عمله منذ عام 1936 ، عندما زار مجموعة الحمراء والحديقة المعمارية في إسبانيا ووجد الإلهام في تكرار الأنماط المتجانبة هناك ، وهي نموذجية للهندسة المعمارية المغربية ، والمعروفة باسم الفسيفساء.

توضح نقوشها على الشجرة "دائرة - حدود" الهندسة الزائدية: تشويه الفضاء مع انحناء سلبي على سطح ثنائي الأبعاد للقرص يشبه تسطيح الكرة الأرضية إلى خريطة ثنائية الأبعاد للأرض ، يشوه شكل القارات. على سبيل المثال ، " الحد - الدائرة الرابعة"(الجحيم والجنة) يشبه الكثير من شخصيات الملائكة والشياطين المتكررة. في الفضاء الزائدي سيكون حجم جميع الأشكال هو نفسه ، ولكن في التمثيلات ثنائية الأبعاد لإيسر ، تبدو الأشكال عند الحافة أصغر مما هي عليه في المركز. مخطط الشبكة الموتر يشبه إلى حد كبير حد" السلسلة " - دائرة "، تمثيل مرئي للروابط العميقة التي وجدها Swing أثناء حضور نفس فئات نظرية الأوتار.

اليوم ، يقتصر تحليل الموتر على نمذجة الزمكان (كما هو الحال في Maldasena) ، التي لا تصف الكون الذي نعيش فيه - ليس لها شكل سرج ، ويتسارع توسعه. يمكن للفيزيائيين الترجمة بين النماذج فقط في حالات خاصة منفصلة. من الناحية المثالية ، يحتاجون إلى "قاموس" عالمي. وهم يرغبون في اشتقاق هذا القاموس مباشرة ، دون استخدام تقريب. يقول بريسكيل: "كنا في وضع مضحك مع هذه الثنائيات لأن الجميع يتفقون على أنها مهمة جدًا ، ولكن لا أحد يعرف كيف يخرجها". "ربما يجعل نهج شبكات الموتر المزيد من التقدم ممكنًا. أعتقد أن علامة التقدم ستكون إذا استطعنا القول ، حتى لو كانت في حالة نموذج لعبة: "آها! ها هو ، ختام القاموس! " سيكون تلميحا خطيرا أننا صادفنا شيئا مهما ".

على مدار العام الماضي ، عمل Swingle و van Raamsdonk معًا لتعزيز عملهما في منطقة تمتد من التمثيل الثابت للزمكان إلى ديناميكي. إنهم مهتمون بكيفية تغير الزمكان مع الوقت وكيف ينحني استجابة لهذه التغييرات. تمكنوا حتى الآن من اشتقاق معادلات أينشتاين ، على وجه التحديد ، مبدأ التكافؤ. هذا يثبت أن ديناميات الزمكان ، مثل هندستها ، تقوم على كيوبتات معقدة. البداية واعدة.

السؤال: ما هو الزمكان؟ يقول فان رامسدونك: يبدو فلسفيًا تمامًا. "في الواقع ، للعثور على إجابة محددة وملموسة تسمح لك بحساب الوقت - سيكون أمرًا رائعًا."

نسيج الكم الزمكان: شبكة نسيج

كيف أزواج الكم غرزة الزمكان

العديد من الهيئات ، شبكة واحدة

حدود الزمكان

More articles: