تريد لغز لاعب الشطرنج المبتدئ؟اطلب منه أن يقضي مع حصان وفيل.هل تريد لغز مبرمج مبتدئ؟اطلب منه حساب الحصيرة مع حصان وفيل. تثير مشاكل الشطرنج خيال المبرمج ،ولهذا السبب في العرض العملي للاندماجيات، اخترت أصعب مشكلة شطرنج من دورة "كش ملك إلى الملك الوحيد".
تثير مشاكل الشطرنج خيال المبرمج ،ولهذا السبب في العرض العملي للاندماجيات، اخترت أصعب مشكلة شطرنج من دورة "كش ملك إلى الملك الوحيد".تحديد الهدف
الهدف من المشروع هو إنشاء قاعدة حل ، أي قائمة بالحركات الصحيحة لجميع المواقع الممكنة للملك الأبيض والفيل والخيول والملك الأسود على رقعة الشطرنج.في هذا المنشور ، سأخبرك كيف قمت بحل هذه المشكلة ، وما هي الصعوبات التي واجهتها ، وسأوضح أيضًا ما حدث في النهاية. التقنيات المستخدمة: C # ، JavaScript ، PHP ، HTML ، CSS.لكوني لاعب شطرنج متواضع للغاية ، لم أتعلم أبدًا كيف أتحدث بسرعة مع حصان وفيل. لذلك ، قررت تعويض هذا القصور بمهاراتي في البرمجة ، وفرز جميع المواقف الممكنة والعثور على الخطوة الصحيحة لكل منها.قبل كتابة سطر واحد على الأقل من التعليمات البرمجية ، قمت بوضع خطة "نابليون" لكيفية القيام بذلك لعدة أسابيع. كنت أرغب حقًا في البدء في حل هذه المشكلة من النهاية ، من خلال الفرز عبر جميع التركيبات غير اللامعة. ثم افعل ذلك خطوة إلى الوراء حتى يتم استنفاد جميع الخيارات الممكنة.كم عدد الخيارات المتاحة؟
هناك 64 خلية على رقعة الشطرنج. لدينا أربعة أرقام.عدد التركيبات الممكنة هو 64 * 64 * 64 * 64 = 16777216.يمكنك ترك فيل أبيض الصدر فقط.سيتم تخفيض عدد الخيارات إلى النصف: 64 * 32 * 64 * 64 = 8،388،608.الكثير من المواقف ستكون في قاعدة البيانات الخاصة بنا للحلول.في الواقع ، هناك مجموعات أقل: قطعتان لا يمكنهما الوقوف على مربع واحد ، لا يمكن للملوك الوقوف على المربعات المجاورة ، لا يمكن أن يكون الملك الأسود تحت الشيك ، وما إلى ذلك. واستشرافا للمستقبل ، سأقول أن قاعدة بيانات الحلول اتضح أنها تركيبات 5،609،790 ، سيتم ملء الصفيف بنسبة 67٪.ومع ذلك ، لتبسيط الخوارزمية وتسريع الوصول إلى بيانات قاعدة البيانات ، قررت عدم "إضاعة الوقت عليها" وإنشاء صفيف رباعي الأبعاد لجميع التركيبات.يتم تعريف البنية التالية لتخزين كل تركيبة: struct Combo
{
public Coord whiteKing;
public Coord whiteBishop;
public Coord whiteKnight;
public Coord blackKing;
}
في الداخل ، يتم استخدام هيكل إحداثي آخر لتسجيل إحداثيات الشكل ، مع القدرة على حساب الفهرس من 0 إلى 63 ، بالإضافة إلى عامل مقارنة زائد الحمل. public struct Coord
{
public byte x;
public byte y;
public int index
{
get { return x + y * 8; }
set { x = (byte) (value % 8);
y = (byte) (value / 8); }
}
public static bool operator == (Coord a, Coord b)
{
return a.x == b.x && a.y == b.y;
}
}
تبين أن هذه البنية مريحة للغاية لتمريرها كحجة إلى وظائف مساعدة مختلفة ، على سبيل المثال: bool isCheck (Combo combo);
bool isCheckmate (Combo combo);
bool isCheckByBishop (Combo combo);
ومع ذلك ، لتسجيل نتيجة قاعدة قرارات هذا الهيكل ليست كافية ، ما زلنا بحاجة ...الصندوق الأبيض
سيكون الهدف من برنامجنا هو إنشاء "مربع أبيض" ، حيث سيتم إضافة جميع المواقف التي تكون فيها "الحركة بيضاء" ، والتي يُعرف عنها أي خطوة يجب اتخاذها ، ومن خلال عدد التحركات التي سيتم ضمانها لشريك.جزء لا يتجزأ من "الصندوق الأبيض" هو الهيكل التالي: struct WhitesMove
{
public Combo combo;
public byte moves;
public Coord moveFrom;
public Coord moveTo;
}
أسهل طريقة لتنظيم "الصندوق الأبيض" هي فتح مصفوفة رباعية الأبعاد. يتوافق كل بُعد من أبعاد هذه المصفوفة مع الموقع المحتمل لكل شكل: WhitesMove [ , , , ] box = new WhitesMove [64, 32, 64, 64];
البعد الأول هو إحداثيات الملك الأبيض.البعد الثاني هو إحداثيات الفيل الأبيض / 2.البعد الثالث هو إحداثيات الحصان الأبيض.البعد الرابع هو إحداثيات الملك الأسود.الشيء الرئيسي هو عدم الخلط بين طلبهم :) سيتحول المصفوفة إلى تفريغها بنسبة 33 ٪ ، ولكنها مريحة جدًا في المعالجة. في هذا الصفيف سيتم تخزين 8388608 إدخالات لحل المجموعات.بالمناسبة ، قبل البدء في كتابة جميع خوارزميات البحث ، قمت بإنشاء مشروع فارغ وقمت بتهيئة هذه المصفوفة رباعية الأبعاد ، للتأكد من وجود ذاكرة كافية ولن يكون من الضروري اختراع شيء إضافي. على ما يبدو ، فإن تجربة المشاركة في الألعاب الأولمبية لعلوم الكمبيوتر في الألفية الماضية ، حيث لا يمكن أن يتجاوز حجم الهيكل 64 كيلو بايت ، أثر على Turbo Pascal 7.0.فكرة الخوارزمية
صف بإيجاز الفكرة الرئيسية لحل هذه المشكلة. وهو يعتمد على خوارزمية بحث واسعة النطاق ، والتي كان لا بد من تعديلها قليلاً ، حيث يلعب شخصان الشطرنج وتتحرك الحركات بدورها. لذلك ، بدلاً من سطر واحد ، نحتاج إلى خطين - "أسود" و "أبيض". Queue<BlacksMove> blackQueue = new Queue<BlacksMove>();
Queue<WhitesMove> whiteQueue = new Queue<WhitesMove>();
مع هيكل WhitesMove التقينا بالفعل. إن بنية BlacksMove أبسط قليلاً ، حيث لا توجد حاجة لتخزين تحرك Black الأخير فيه.struct BlacksMove
{
public Combo combo;
public byte moves;
}
أولاً ، في "الخط الأسود" ، سنضع جميع المواضع غير اللامعة التي تكون فيها الحركة سوداء. ثم من كل موقف من هذا القبيل ، سنقوم بحركة عكسية للأبيض ونشكل "خطًا أبيض" - قائمة بالمواقع التي يتحرك فيها الأبيض.يجب تكرار هذه الخطوات حتى يتم استنفاد جميع التركيبات الممكنة.الخوارزمية الرئيسية في شكل كود زائف: " ", " ", " "
" "
{
" "
" "
" "
" "
" "
" "
" "
" "
" "
} " "
" "
موقف غير لامع
يبدأ إنشاء قاعدة التحركات الصحيحة بالبحث عن جميع المجموعات غير اللامعة. جعل استخدام العدادات من الممكن وصف هذه العملية بشكل فعال. foreach (Combo combo in AllCheckmates())
{
BlacksMove checkmate = new BlacksMove { combo = combo, moves = 0 };
blackQueue.Enqueue(checkmate);
}
تم العثور على 232 موضع غير لامع. دعني أذكرك بأننا اقتصرنا على فيل أبيض اللون فقط.بعضها غريب نوعًا ما و "غير متعاون" و "متعاون" ، هذا عندما صعد الملك الأسود نفسه تحت الحصيرة. يدرك لاعبو الشطرنج جيدًا أنه يجب وضع حصيرة مع حصان وفيل أبيض في زاوية بيضاء. في الركن الأسود ، يكون كش ملك ممكنًا فقط إذا كان الأسود سيلعب على طول. لقد نشرت صورة خاصة مع مثل هذا الزائفة الآلية في بداية المقال من أجل إثارة انتباه لاعبي الشطرنج الحقيقيين :)
يدرك لاعبو الشطرنج جيدًا أنه يجب وضع حصيرة مع حصان وفيل أبيض في زاوية بيضاء. في الركن الأسود ، يكون كش ملك ممكنًا فقط إذا كان الأسود سيلعب على طول. لقد نشرت صورة خاصة مع مثل هذا الزائفة الآلية في بداية المقال من أجل إثارة انتباه لاعبي الشطرنج الحقيقيين :)حصيرة في خطوة واحدة
الخطوة التالية هي عكس الأبيض. هذا هو ، لكل موقف غير لامع موجود ، قم بكل التحركات البيضاء الممكنة .كيفية القيام بحركة عكسية؟ بالنظر إلى أنه لم يتم توفير التقاط في مواقفنا ، فإن الخوارزمية بسيطة للغاية - قم بأي تحرك بواسطة White ، وبعد ذلك لن يكون هناك فحص للملك الأسود.يمكن بالفعل وضع جميع المواقف الموجودة بهذه الطريقة في "الصندوق الأبيض" ، مما يشير إلى وجود حركة واحدة قبل الحصيرة ، ونوع الحركة للقيام بذلك. على طول الطريق ، نضع المجموعات الموجودة في "الخط الأسود".إليك ما يبدو عليه هذا الجزء من الخوارزمية:
while (blackQueue.Count > 0)
{
BlacksMove black = blackQueue.Dequeue();
foreach (WhitesMove white in AllWhiteBackMoves(black))
if (!isCheck(white.combo))
if (!whiteBox.Exists(white.combo))
{
whiteBox.Put (white);
whiteQueue.Enqueue(white);
}
}
بالمناسبة ، حول العائدyield- , , :
IEnumerable<WhitesMove> AllWhiteBackMoves(BlacksMove black)
{
foreach (WhitesMove white in AllWhiteKingMoves(black))
yield return white;
foreach (WhitesMove white in AllWhiteBishopMoves(black))
yield return white;
foreach (WhitesMove white in AllWhiteKnightMoves(black))
yield return white;
}
تم العثور على ما مجموعه 920 من هذه المواقف ، وهنا الأكثر إثارة للاهتمام: حركةالحصان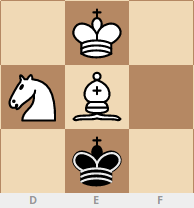

 :
: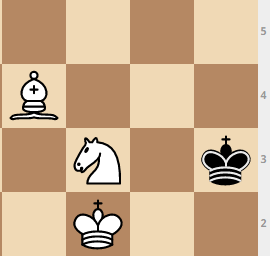
 حركة الفيل : حركة الملك:
حركة الفيل : حركة الملك: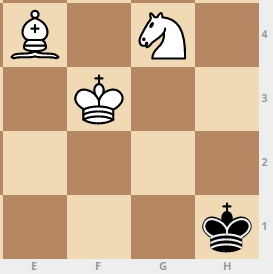
حصيرة في حركات ونصف
الخطوة التالية هي عكس الأسود. مع هذه الخوارزمية قضيت أطول وقت ، تم ارتكاب الكثير من الأخطاء قبل أن يعمل كل شيء بشكل صحيح.للوهلة الأولى ، كل شيء مشابه للإصدار السابق: لكل موقع من "الخط الأبيض" من الضروري فرز جميع التحركات المحتملة للملك الأسود. وأضف جميع التركيبات الموجودة إلى "الخط الأسود" - بعد كل شيء ، هذا هو كش ملك في حركات ونصف ، حيث يمكنك بعد ذلك القيام بحركة عكسية للأبيض مرة أخرى - سيكون هناك كش ملك في حركتين - والاستمرار حتى تتم مراجعة جميع الخيارات.كان هذا هو الخطأ. مع أي تحرك محتمل ، يحصل الأسود على رفيق "تعاوني" في حركات ونصف ، ولكن في الواقع لن يخوض الملك بالضرورة تحت كش ملك. أشار ديميتري غرين إلي هذا الخطأ ، الذي حضر جميع ندواتي على الإنترنت حول إنشاء هذا البرنامج ، وأشكره على حدة.الخوارزمية الصحيحة هي كما يلي: لكل موضع N بعد الحركة العكسية للملك الأسود ، تحتاج إلى المرور بكل الحركات المباشرة الممكنة للتأكد من أنها تؤدي جميعها إلى مواقف مألوفة من "المربع الأبيض" ، أي تؤدي إلى الحصيرة. وبعد ذلك فقط يمكن إضافة الموضع N إلى "الخط الأسود". وإذا تمكن الملك الأسود من "الابتعاد" عن الموضع N ، فإننا نتخطى هذا الخيار. سوف تجتمع في التكرارات اللاحقة ، عندما تكون هناك مواقف مألوفة أكثر.إليك ما يبدو عليه هذا الجزء من الخوارزمية:
while (whiteQueue.Count > 0)
{
WhitesMove white = whiteQueue.Dequeue();
Combo whiteFigures = white.combo;
foreach (BlacksMove black in AllBlackBackMoves(white))
{
bool solved = true;
foreach (Coord blackKing in AllKingMoves(black.combo.blackKing))
{
whiteFigures.blackKing = blackKing;
if (isCheck(whiteFigures))
continue;
if (box.Exists(whiteFigures))
continue;
solved = false;
break;
}
if (solved)
blackQueue.Enqueue(black);
}
}
في المجموع ، تم العثور على 156 مجموعة من "حصيرة ونصف التحركات".التكرار في منتصف الطريق
يجب أن يتم تكرار الخوارزميات الموصوفة لإنشاء نصف تمرير. من "الخط الأسود" نشكل "الخط الأبيض" ، والعكس صحيح - من الخط "الأبيض" نشكل "الخط الأسود". وهكذا حتى يتم استنفاد جميع المواقف الجديدة. يتم ملء "الصندوق الأبيض" في مرحلة تكوين "الخط الأبيض" ، حيث يضع المواضع التي يتحرك فيها الأبيض.عملت الخوارزمية الجاهزة لتعداد جميع الخيارات في مكان ما خلال 12 دقيقة وتوقفت عند الخطوة 33. هذا هو عدد الحركات القصوى اللازمة لتزاوج الملك الأسود مع حصان وفيل من أي موقع.بالمناسبة ، لم يكن هناك الكثير من هذه المواقف "الأكثر صعوبة" ، فقط 156 ، وهنا أحدها:
لن يكون ماتا!
هناك العديد من المواقف ، حتى بعد تحرك وايت ، يمكن للملك الأسود أن يأكل فارسًا أو أسقفًا ويحصل على التعادل. هناك أيضا خيارات الجمود. فيما يلي بعض العناصر الأكثر إثارة للاهتمام.
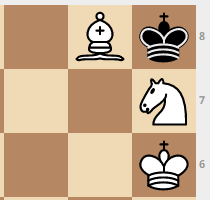


كيفية تخزين قاعدة بيانات الحل
كيفية تخزين قاعدة الحل التي تم العثور عليها؟الطريقة الأسهل والخطأ هي استخدام التسلسل. استغرق الصفيف المتسلسل رباعي الأبعاد للهيكل 1.7 غيغابايت (!) من مساحة القرص. استغرقت عملية التسلسل حوالي ست دقائق ، واستغرقت عملية إزالة التسلسل نفسها.هذا الخيار ، بالطبع ، غير مناسب. بالإضافة إلى ذلك ، في الممارسة العملية ليست هناك حاجة لاستخدام كامل مجموعة الأبعاد الأربعة. يلزم إدخال واحد فقط لبند معين.أوريكا! لتوفير مساحة ، لا يزال بإمكانك التخلص من تخزين إحداثيات الأشكال لكل تركيبة. عندما يكون لدينا صفيف رباعي الأبعاد ، يتم تحديد موضع كل شكل على اللوحة بشكل فريد من خلال فهرسه في الصفيف.تقرر تخزين قاعدة البيانات الكاملة للحلول في ملف واحد - كمسح خطي على صفيف رباعي الأبعاد. بالنسبة لأي موضع محتمل ، يتم حساب العنوان الذي يتم تسجيل الإجابة الصحيحة عنده.كيف نسجل الإجابة التي نحتاجها بأكبر قدر ممكن؟ لا يلزم تخزين موضع الأرقام ، لذلك تبقى ثلاثة أرقام فقط - عدد التحركات إلى الحصيرة ، وماذا تذهب وأين تذهب. هذه هي الطريقة التي يتم بها تحديد الخطوة الصحيحة للأبيض بشكل فريد.6 بت عدد التحركات إلى الحصيرة عدد صحيح من 0 إلى 33.2بت. ما يمشي الرقم - ثلاثة خيارات ممكنة ، ملك أو فيل أو حصان.6 بت أين تذهب القطعة - فهرس المجال على السبورة من 0 إلى 63.لذا ، لكل سجل قرار ، يكفي وحدتي بايت:1 بايت - عدد التحركات إلى الحصيرة ، أو 0 إذا كان الموضع غير مألوف.2 بايت - FFNNNNNNFF - رقم الشكل الذي سيتم السير فيه (1 - الملك ، 2 - الفيل ، 3 - الحصان)NNNNNN - إحداثيات الخلية - إلى أين تذهب (من 0 إلى 63).لذلك ، يأخذ ملف قاعدة بيانات الحل 64 * 32 * 64 * 64 كلمة = 16 ميغابايت بالضبط. يتم تعيين موضع الأشكال من إحداثيات كل كلمة ، في البايت الأول - عدد التحركات إلى الحصيرة (أو 0 إذا لم يكن هناك حل) ، تخزن الخطوة الثانية النقل الصحيح.سيكون من الممكن تقليل حجم الملف إلى النصف إذا لم تقم بتخزين عدد الحركات إلى الحصيرة ، ولكن لن يكون من المثير للاهتمام اللعب بهذه الطريقة.إحداثيات الفيل الأبيض المربع الأسود
حان الوقت للدفع مقابل التحسين. من الضروري تنفيذ خوارزمية إعادة حساب إحداثيات للمجموعات مع فيل "أبيض وأسود".تم ذلك على النحو التالي. إذا وقعت إحداثيات الفيل على حقل أسود ، فيجب عندئذٍ "قلب" إحداثيات جميع الأشكال الموجودة على اللوحة. في هذه الحالة ، تظل إحداثيات Y بدون تغيير ، وتتغير X إلى 7-X. عرض مرئي لقلب إحداثيات ، انظر الشكل. إذا كان الفيل يقف على قفص أبيض ، فأنت بحاجة أولاً إلى "قلب" إحداثيات جميع الأشكال. ثم ابحث عن موضع في قاعدة بيانات الحلول. ومرة أخرى "اقلب" إحداثيات الحركة الصحيحة من هناك.
إذا كان الفيل يقف على قفص أبيض ، فأنت بحاجة أولاً إلى "قلب" إحداثيات جميع الأشكال. ثم ابحث عن موضع في قاعدة بيانات الحلول. ومرة أخرى "اقلب" إحداثيات الحركة الصحيحة من هناك.تصور قاعدة الحل
لذا ، تم حل المشكلة!تم إنشاء قاعدة القرار.ولكن كيف تثبت ذلك؟الطريقة الأكثر وضوحًا هي استخدام تقنيات الويب بحيث يمكنك فقط إعطاء رابط لمثال عملي. في "صيغة المبرمج" الخاصة بي ، تم بالفعل إنشاء دورة الصور " Nano-Chess " ، حيث تم استخدام تقنيات الشطرنج التفاعلية للعب بدون قواعد لشخصين باستخدام تقنيات HTML و CSS و JavaScript و PHP. تم أخذ هذا البرنامج النصي كأساس.لقد تركت أربع قطع فقط ، وأزلت إمكانية الالتقاط ، وأضفت وظائف PHP لقراءة التحركات الصحيحة من قاعدة الحلول ، و "تنفس الهواء" من خلال JavaScript.على الصفحة www.videosharp.info/chess يمكنك تجربة قاعدة بيانات الحلول. لكل موقف ، يتم حساب التحركات لكل من الأبيض والأسود.للأبيض - أفضل خطوة تؤدي إلى كش ملك.للأسود - عدد التحركات إلى الحصيرة لأي حركة محتملة.يمكنك القيام بأي حركة للأشكال باستخدام الماوس ، وليس بالضرورة وفقًا للقواعد.سيحسب البرنامج النصي خيار أي موضع ، أو يكتب أنه لا توجد خيارات.من المثير للاهتمام اللعب أو تنفيذ التحركات المقترحة أو تحريك القطع حسب تقديرك.
لكل موقف ، يتم حساب التحركات لكل من الأبيض والأسود.للأبيض - أفضل خطوة تؤدي إلى كش ملك.للأسود - عدد التحركات إلى الحصيرة لأي حركة محتملة.يمكنك القيام بأي حركة للأشكال باستخدام الماوس ، وليس بالضرورة وفقًا للقواعد.سيحسب البرنامج النصي خيار أي موضع ، أو يكتب أنه لا توجد خيارات.من المثير للاهتمام اللعب أو تنفيذ التحركات المقترحة أو تحريك القطع حسب تقديرك.الخلاصة
تم عمل رائع ومثير للاهتمام لحل مشكلة الشطرنج.إذا كنت تريد التكرار بهذه الطريقة ، يمكنك مشاهدة مقاطع فيديو حول إنشاء هذا البرنامج من البداية إلى النتيجة مع شرح مفصل ومهام مستقلة.حظا سعيدا!