كيفية قطع الكعكة بشكل عادل
طور علماء الكمبيوتر خوارزمية دائرية عادلة لأي عدد من الناس
اكتشف عالما شابان ، خبراء في مجال علوم الكمبيوتر ، كيفية مشاركة الكعكة بصدق بين أي عدد من الأشخاص ، وحل المشكلة التي يعاني منها علماء الرياضيات منذ عقود. فاجأ عملهم العديد من الباحثين الذين اعتبروا أن هذا الفصل مستحيل من حيث المبدأ.مشاركة فطيرة هي استعارة لمجموعة واسعة من المهام الواقعية ، بما في ذلك تقسيم كائن مستمر معين ، سواء كان كعكة أو قطعة أرض ، بين الأشخاص الذين يقدرون خصائصه بشكل مختلف. واحد يحب طلاء الشوكولاتة ، والآخر يريد زهور كريم. منذ العصور التوراتية ، عرفت الخوارزمية بتقسيم مثل هذا الشيء بين شخصين ، بحيث لا يحسد أحدهما الآخر: يقسم أحدهم الكعكة إلى قسمين متساويين ، والآخر يختار أحدهما. في سفر التكوين ، استخدم إبراهيم (المعروف آنذاك باسم أبرام) ولوط هذه الطريقة لتقسيم الأرض ، عندما اخترع إبراهيم انفصالًا ، واختار لوط بين الأردن وكنعان.في الستينيات ، توصل علماء الرياضيات إلى خوارزمية لمثل هذه الكعكة المنقسمة "بدون حسد" لثلاثة أشخاص. ولكن حتى الآن، كان الحل الأفضل للمشكلة لكثير من الناس أكثر من ثلاثة الإجراءات، التي أنشئت في عام 1995 في العلوم السياسية ستيفن برامز [ستيفين برامز] من جامعة نيويورك وعالم الرياضيات آلان تايلور [آلان تايلور] من كلية الاتحاد. لقد كفلت مشاركة "عادلة" للكيك ، ولكن بشرط واحد - كان الإجراء "غير محدود" ، أي أن عدد الخطوات المطلوبة للمشاركة سيكون تعسفيًا.كانت خوارزمية برامز-تيلور تسمى مرة اختراق ، ولكن "في رأيي ، كان عيبًا غير محدود ،" يقول أرييل بروكاتشيا[أرييل بروكاتشيا] ، عالم كمبيوتر في جامعة كارنيجي ميلون ، أحد مبدعي Spliddit ، وهي أداة مجانية عبر الإنترنت للمشاركة العادلة في المهام ، من واجبات الأسرة إلى رسوم الإيجار المشتركة.على مدى الخمسين عامًا الماضية ، أقنع العديد من علماء الرياضيات وعلماء الكمبيوتر ، بما في ذلك Procaccia ، أنفسهم بأنه لا توجد خوارزمية عادلة محدودة لتقسيم الكعكة إلى أجزاء n.يقول والتر سترومكفيست: "كانت هذه المهمة هي التي قادتني إلى منطقة الانقسامات العادلة"[والتر سترومكويست] ، أستاذ الرياضيات في كلية برين مافر في ولاية بنسلفانيا ، والذي حقق نتائج جيدة في مشكلة مشاركة الكعكة في عام 1980. "طوال حياتي اعتقدت أنني سأعود إلى هذه المهمة في وقت فراغي وأثبت أن مثل هذا التمديد للنتيجة مستحيل من حيث المبدأ" .لكن في أبريل ، دحض متخصصان في علوم الكمبيوتر هذه التوقعات من خلال نشر خوارزمية للمشاركة العادلة للكعكة مع وقت التشغيل اعتمادًا على عدد المشاركين في المشاركة ، وليس على تفضيلاتهم الشخصية. قدم أحد العلماء ، سيمون ماكنزي ، 27 عامًا ، دكتوراه من كارنيجي ميلون ، عمله في 10 أكتوبر في أساسيات علوم الكمبيوتر IEEE السنوية السابعة والخمسين.الخوارزمية معقدة للغاية. قد يتطلب قسم الكيك بين المشاركين n حتى nن ن ن ن ن الخطوات، مع حوالي نفس العدد من الأبواب. حتى بالنسبة لعدد قليل من المشاركين ، يتجاوز هذا العدد عدد الذرات في الكون. لكن الباحثين لديهم بالفعل أفكار لتبسيط وتسريع الخوارزمية ، وفقًا لعضو الفريق الثاني ، حارس عزيز ، المتخصص في علوم الكمبيوتر البالغ من العمر 35 عامًا في جامعة نيو ساوث ويلز ، والذي يعمل في مجموعة أبحاث البيانات الأسترالية Data61. يرىالخبراء الذين يدرسون نظرية التقسيم العادل ، وفقًا لـ Procaccia ، أن هذه "بالتأكيد أفضل نتيجة لعقود".قطع من الكيك
تعتمد خوارزمية عزيز وماكينزي على إجراء أنيق تم اختراعه بشكل مستقل من قبل علماء الرياضيات جون سيلفريدج وجون كونواي في الستينيات ، والذي يسمح لك بتقسيم كعكة إلى ثلاثة إلى حد ما.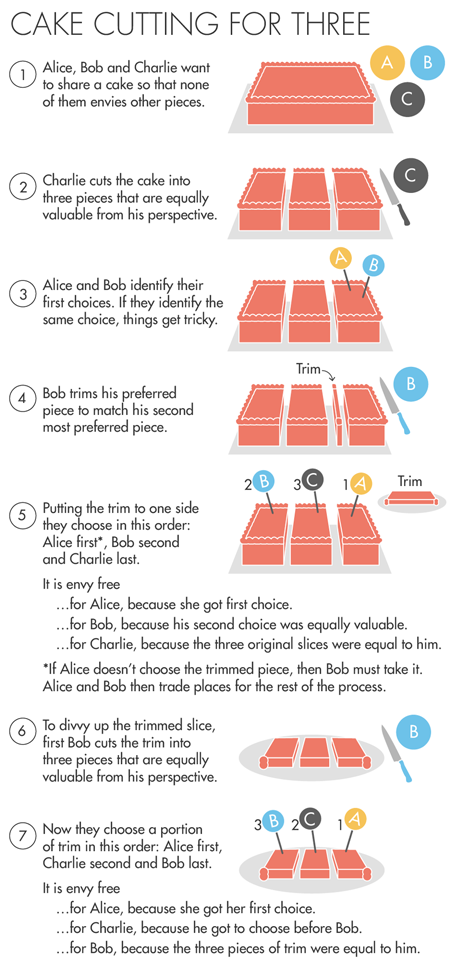
إذا أرادت أليس وبوب وتشارلي (أ ، ب ، ج) تقسيم الكعكة ، تبدأ الخوارزمية بتقسيم تشارلي الكعكة إلى ثلاث قطع تبدو متشابهة بالنسبة له. تختار أليس وبوب القطع التي تعجبهما. إذا اختاروا قطعًا مختلفة - فويلا ، يحصل الجميع على ما يريدون.إذا اختار أليس وبوب قطعة واحدة ، فسيقوم بوب بقطع جزء صغير من هذه القطعة بحيث تصبح القطعة متكافئة ، من وجهة نظره ، إلى قطعة أخرى من الكعكة - تلك التي سيختارها بوب في المركز الثاني. تم تأجيل بقايا القطع. الآن يجب أن تختار أليس أفضل قطعة لنفسها من الثلاثة المتبقية ، ثم تختار بوب - بشرط أن يأخذ قطعة القطع من قبله ، إذا لم تحدد أليس ذلك. تشارلي يحصل على القطعة الثالثة.ونتيجة لذلك ، لا أحد يحسد أحدا. اختار أليس الأول. تلقى بوب واحدة من قطعتين له نفس القيمة. حصل تشارلي على واحدة من القطع الأصلية الثلاث التي قطعها بنفسه.فقط قطع صغيرة باقية. ولكن يمكن تقسيمها دون بدء الخوارزمية أولاً ودون الوقوع في دائرة لا نهاية لها من الختان والاختيارات ، حيث أن تشارلي راضٍ على أي حال عن قطعته - وحتى لو كان الشخص الذي حصل على القطعة سيحصل على الباقي بالكامل في الملحق بها ، لأنه لن يبدو تشارلي غير شريف ، لأن القطعة المقطوعة والباقي سيعطي قطعة من الكعكة تعادل قطعتها - بعد كل شيء ، قام بقطع هذه القطع من البداية. يصف عزيز وماكينزي موقف تشارلي بأنه "مهيمن".الآن ، على سبيل المثال ، إذا حصلت Alice على قطعة القطع ، يقوم Bob بتقطيع القطع إلى ثلاثة أجزاء ، أي ما يعادل وجهة نظره ، تختار Alice واحدة من هذه القطع لنفسها ، ثم تختار Charlie ، ثم Bob. الجميع سعداء: اختارت أليس أولاً ، وحصلت تشارلي على قطعة أفضل من بوب (ولا يهتم بالكم الذي استهلكته أليس) ، ومن وجهة نظر بوب ، فإن القطع الثلاث متساوية.استخدم برامز وتايلور خاصية "الهيمنة" (ولكن باسم مختلف) لتطوير خوارزمية عام 1995 ، لكنهما لم ينهيا فكرتهما حتى ظهرت خوارزمية محدودة. في السنوات ال 20 المقبلة ، لم يحقق أحد أفضل النتائج. يقول بروكاشيا: "وليس بسبب قلة المحاولات".مقسمات كعكة غير مهنية
عندما قرر عزيز وماكينزي (A&M) تولي هذه المهمة قبل عامين ، كانا جديدين في مهمة مشاركة الكعكة. قال عزيز: "لم تكن لدينا خبرة مثل الأشخاص الذين عملوا بشكل مكثف عليها". "على الرغم من أن هذا عادة ما يكون عيبًا ، إلا أنه في حالتنا كان ميزة ، لأننا فكرنا بشكل مختلف."بدأ A&M بدراسة مهمة التقسيم إلى ثلاثة مشاركين من البداية ، ونتيجة للتحليل ، تم التوصل إلى خوارزمية عادلة محدودة لأربعة مشاركين ، نشروها العام الماضي.لم يتمكنوا من إظهار كيفية توسيع الخوارزمية الخاصة بهم على الفور إلى عدد من المشاركين أكبر من أربعة ، لكنهم أخذوا هذه المهمة بحماس. يقول عزيز: "بعد إرسال العمل فيما يتعلق بأربعة مشاركين ، أردنا حقًا مواصلة العمل بسرعة حتى يقوم شخص أكثر خبرة بتعميمه بشكل ذكي على حالة المشاركين". وبعد حوالي عام ، كان بحثهم ناجحًا.مثل خوارزمية Selfridge-Conway ، يقدم بروتوكول AiM باستمرار مشاركين مختلفين لقطع الكعكة إلى أجزاء متساوية ، وآخرون لقطع واختيار قطع الكعكة. ولكن هناك خطوات أخرى في الخوارزمية ، على سبيل المثال ، التبادل الدوري لقطع الكعك بطريقة خاصة ، من أجل زيادة عدد العلاقات السائدة بين المشاركين.تسمح هذه العلاقات لشركة A&M بتقليل تعقيد المهمة. إذا ، على سبيل المثال ، سيطر ثلاثة مشاركين على البقية ، فيمكن بالفعل إرسالهم لتناول قطع الكعكة الخاصة بهم - سيكونون سعداء بغض النظر عن من يحصل على بقايا الطعام. بعد ذلك ، يبقى عدد أقل من المشاركين ، وبعد عدد محدود من هذه الخطوات ، يشعر الجميع بالرضا ويتم تقسيم الكعكة بأكملها.يقول بروكاتشيا: "بالنظر إلى مدى تعقيد الخوارزمية ، فإنه ليس من المستغرب أن يستغرق تطويرها وقتًا طويلاً". ولكن حاييم نعتقد بالفعل أنها يمكن تبسيط الخوارزمية، بحيث أنها لا تتطلب تبادل القطع ومرت للتو ن ن ن الخطوات. وبحسب عزيز ، فإنهم يعملون بالفعل على هذه النتائج.يحذر برامز من أنه حتى الخوارزمية الأبسط لن يكون لها تطبيق عملي - بعد كل شيء ، فإن قطع الكعكة التي يتلقاها المشاركون ستشمل العديد من الفتات الصغيرة من أجزاء مختلفة من الكعكة. هذا النهج غير مفيد بشكل خاص إذا كنت تقسم الأرض ، على سبيل المثال.ولكن بالنسبة لعلماء الرياضيات والكمبيوتر الذين يدرسون المشكلة ، فإن النتيجة الجديدة "تعيد تعيين الموضوع بأكمله" ، كما يقول سترومكفيست.الآن بعد أن عرف الباحثون أن الكعكة يمكن تقسيمها في عدد محدود من الخطوات ، فإن الخطوة التالية ، وفقًا لـ Procaccia ، هي فهم الفجوة الكبيرة بين الحد الأعلى لعدد الخطوات بطريقة AiM والحد الأدنى لعدد الخطوات اللازمة لذلك. أثبتت Procaccia بالفعل في وقت سابق أن خوارزمية الفصل العادل للكعكة لا يمكن أن تمر في أقل من n2 الخطوات - ولكن هذا عدد صغير من الخطوات بالمقارنة مع ن ن ن ن ن ن وحتى ن ن ن .يقول عزيز إن على الباحثين الآن معرفة كيفية تضييق هذه الفجوة. "أعتقد أنه يمكن إحراز تقدم في كلا الاتجاهين."Source: https://habr.com/ru/post/ar398683/
All Articles