لن أكذب ، إنني أتطلع حقًا إلى فيلم Spider-Man: Homecoming [Spider-Man: Homecoming]. في هذه الأثناء ، سيكون المنفذ الوحيد بالنسبة لي هو القيام بفيزياء الرجل العنكبوت. وسأعتني بجناحه العنكبوتي الجديد الذي شوهد في المقطع الدعائي الأخير.بالنسبة للمعجبين ، ألاحظ أن بعض القصص المصورة الأصلية عن الرجل العنكبوت أظهرت حقًا كيف يستخدمها ، على الرغم من أنه لم يستخدمها دائمًا للطيران.التخطيط الفيزيائي
ماذا يحدث بعد أن قفز الرجل العنكبوت من مبنى؟ يمكنني محاكاة حركته بقبول أن ثلاث قوى تعمل عليه - الجاذبية ، ومقاومة الهواء ، والرفع. بإذنكم ، سأصف كل واحد منهم.• الجاذبية - قوة نزولية ثابتة تتناسب مع كتلة الطوارئ (على الأقل على سطح الأرض).• المقاومة. تخيل أنك تسحب شيئًا عبر بحر عملاق من كرات كرة الطاولة. استبدل الكرات بالهواء - وستكون هي نفسها تقريبًا. تزداد المقاومة مع السرعة.• قوة الرفع. مرة أخرى ، تخيل التصادمات مع الكرات ، ولكن تلك التي بعدها ترتد الكرات. باستبدال الكرات بالهواء ، سوف تتلقى رفعًا اعتمادًا على زاوية الهجوم والسطح والسرعة.هنا رسم جميل لقوى شخص يخطط لأجنحة الطوارئ. نعم ، بينما نمثلها بمثلث.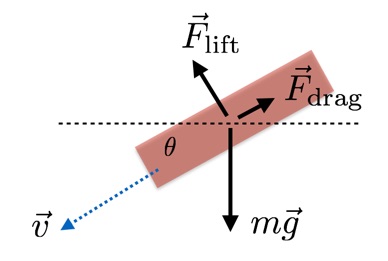 في نموذجنا البسيط ، تكون قوة الرفع متعامدة على السرعة ، ويتم توجيه المقاومة في الاتجاه المعاكس. لمحاكاة حركة الطوارئ بالأجنحة ، أحتاج إلى صيغة لكليهما.
في نموذجنا البسيط ، تكون قوة الرفع متعامدة على السرعة ، ويتم توجيه المقاومة في الاتجاه المعاكس. لمحاكاة حركة الطوارئ بالأجنحة ، أحتاج إلى صيغة لكليهما.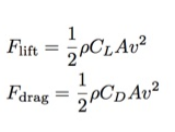 هذه هي قيم القوى التي تهمنا. وهما متشابهان ، باستثناء C L (معامل الرفع) و C D (معامل السحب). في كلتا الحالتين ، ρ هي كثافة الهواء (1.2 كجم / م 3 ) ، و v هي السرعة.ما هو A؟ هذه هي المنطقة المستعرضة للشخص (الطوارئ في حالتنا). من الناحية النظرية ، يجب أن تختلف المقاومة A وقوة الرفع ، اعتمادًا على زاوية الهجوم. لكنني لا أعرف دائمًا ما أفعله بالضبط - لهذا السبب راجعت مصادر مختلفة ، ومقال عام 2011 " مسار سقوط باتمان"من المجلة الفيزيائية Journal of Physics Special Topics. استخدم فيها المؤلفون نفس المنطقة للمقاومة والرفع ، لذلك سأفعل نفس الشيء.
هذه هي قيم القوى التي تهمنا. وهما متشابهان ، باستثناء C L (معامل الرفع) و C D (معامل السحب). في كلتا الحالتين ، ρ هي كثافة الهواء (1.2 كجم / م 3 ) ، و v هي السرعة.ما هو A؟ هذه هي المنطقة المستعرضة للشخص (الطوارئ في حالتنا). من الناحية النظرية ، يجب أن تختلف المقاومة A وقوة الرفع ، اعتمادًا على زاوية الهجوم. لكنني لا أعرف دائمًا ما أفعله بالضبط - لهذا السبب راجعت مصادر مختلفة ، ومقال عام 2011 " مسار سقوط باتمان"من المجلة الفيزيائية Journal of Physics Special Topics. استخدم فيها المؤلفون نفس المنطقة للمقاومة والرفع ، لذلك سأفعل نفس الشيء.نمذجة المسار
إذا قفزت حالة الطوارئ من مبنى ، إلى أي مدى يمكن أن تتحرك في السقوط؟ ما الفرق الذي ستعطيه له أجنحة العنكبوت؟ إن نمذجة حالة الطوارئ ليست بهذه البساطة ، لأن المقاومة والرفع يعتمدان على السرعة. لا يمكن حساب هذا المسار إلا باستخدام نموذج رقمي يتم فيه تقسيم الحركة إلى خطوات صغيرة.فلنقم بالتقريب. أولاً ، نحسب مساحة سطح الطوارئ. تقريبًا ، حصلت على: ما يعطينا مساحة حوالي 0.651 م 2 مع أجنحة و 0.513 م 2 بدونها. قيم أخرى:• معامل الرفع = 1.45 (القيمة مأخوذة من عمل باتمان)• معامل المقاومة = 0.4 (من نفس المكان)• الوزن = 64 كجم• السرعة الأولية = 8 م / ث (أفقيًا)• وافتراض واحد آخر: زاوية هجوم ثابتة ، فيما يتعلق بمعاملي السحب والرفع لا يتغيران.دون تردد ، قفزت إلى عالم النماذج العددية. تركت تعليقات في الشفرة بحيث يمكنك إعادة تشكيلها لاستخدامها في الواجبات المنزلية.
ما يعطينا مساحة حوالي 0.651 م 2 مع أجنحة و 0.513 م 2 بدونها. قيم أخرى:• معامل الرفع = 1.45 (القيمة مأخوذة من عمل باتمان)• معامل المقاومة = 0.4 (من نفس المكان)• الوزن = 64 كجم• السرعة الأولية = 8 م / ث (أفقيًا)• وافتراض واحد آخر: زاوية هجوم ثابتة ، فيما يتعلق بمعاملي السحب والرفع لا يتغيران.دون تردد ، قفزت إلى عالم النماذج العددية. تركت تعليقات في الشفرة بحيث يمكنك إعادة تشكيلها لاستخدامها في الواجبات المنزلية.GlowScript 2.1 VPython
A1=0.651
A2=0.513
g=vector(0,-9.8,0)
m=64
CL=1.45
CD=0.4
rho=1.2
v0=8
p=vector(v0,0,0)*m
p2=p
t=0
dt=0.01
h=40
r=vector(0,h,0)
r2=r
f1=series(color=color.red)
f2=series(color=color.blue)
while r.y>0:
v=p/m
v2=p2/m
Fd=-.5*rho*A1*CD*(mag(v)**2)*norm(v)
Fd2=-.5*rho*A2*CD*(mag(v2)**2)*norm(v2)
FL=-.5*rho*A1*CL*(mag(v)**2)*cross(norm(v),vector(0,0,1))
FL2=-.5*rho*A2*CL*(mag(v2)**2)*cross(norm(v2),vector(0,0,1))
F=m*g+Fd+FL
F2=m*g+Fd2+FL2
p=p+F*dt
p2=p2+F2*dt
r=r+p*dt/m
r2=r2+p2*dt/m
t=t+dt
f1.plot(r.x,r.y)
f2.plot(r2.x,r2.y)
print("Glide Ratio 1 = ",-p.x/p.y)
print("Glide Ratio 2 = ", -p2.x/p2.y)
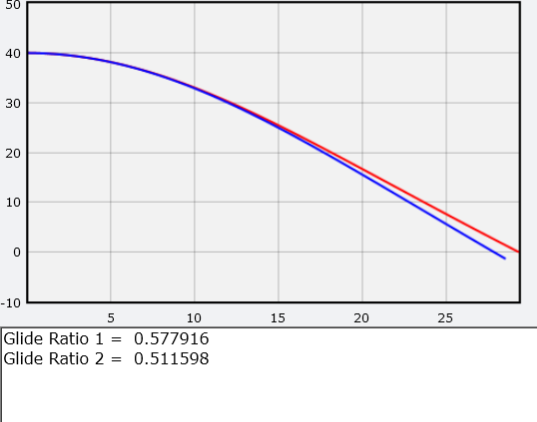 في نموذجي ، يمثل الخط الأحمر مسار الطوارئ بالأجنحة ، والخط الأزرق بدون أجنحة. أستمد أيضًا قيمة الجودة الديناميكية الهوائية. نظرًا لأنه في النهاية يتحرك بسرعة ثابتة ، فإن هذه النسبة ستكون ببساطة مساوية لنسبة مكون x في الزخم مقسومًا على مكون y.الواجب المنزلياستخدم هذا النموذج العددي للإجابة على الأسئلة التالية . لا تقلق ، لن تكسر أي شيء. إذا قمت بشيء ما باستخدام الرمز ، فما عليك سوى إعادة التشغيل والبدء من جديد.• وفقًا لويكيبيديا، بالنسبة للقفز المظلي الذي يرتدي بدلة مجنحة ، فإن جودة الديناميكية الهوائية (نسبة الرفع إلى السحب) تبلغ قيمتها 2.5: 1 (أي أن برنامجنا سوف يستنتج الرقم 2.5). هل يمكنك تصحيح الكود بحيث ينتج البرنامج مثل هذه القيمة؟ تلميح: قم بتغيير مساحة السطح والسرعة الأولية.• ماذا لو سقطت حالة الطوارئ عموديا؟ ما هي السرعة القصوى التي ستكسبها مع الأجنحة وبدونها؟• ما مدى سرعة تحرك الطوارئ أفقيًا بحيث تطير لأعلى بدلاً من النزول عند بدء الرحلة؟• هل يمكن أن تقفز الطوارئ ، وتهدف إلى الأسفل ، من أجل اكتساب المزيد من السرعة والذهاب لبعض الوقت في رحلة أفقية؟• هل يمكنك بناء نموذج محسن يأخذ في الاعتبار زاوية الهجوم؟ ربما يمكنك ذلك ، ولكن يبدو لي أن الطيران بسرعة منخفضة موضوع معقد إلى حد ما.
في نموذجي ، يمثل الخط الأحمر مسار الطوارئ بالأجنحة ، والخط الأزرق بدون أجنحة. أستمد أيضًا قيمة الجودة الديناميكية الهوائية. نظرًا لأنه في النهاية يتحرك بسرعة ثابتة ، فإن هذه النسبة ستكون ببساطة مساوية لنسبة مكون x في الزخم مقسومًا على مكون y.الواجب المنزلياستخدم هذا النموذج العددي للإجابة على الأسئلة التالية . لا تقلق ، لن تكسر أي شيء. إذا قمت بشيء ما باستخدام الرمز ، فما عليك سوى إعادة التشغيل والبدء من جديد.• وفقًا لويكيبيديا، بالنسبة للقفز المظلي الذي يرتدي بدلة مجنحة ، فإن جودة الديناميكية الهوائية (نسبة الرفع إلى السحب) تبلغ قيمتها 2.5: 1 (أي أن برنامجنا سوف يستنتج الرقم 2.5). هل يمكنك تصحيح الكود بحيث ينتج البرنامج مثل هذه القيمة؟ تلميح: قم بتغيير مساحة السطح والسرعة الأولية.• ماذا لو سقطت حالة الطوارئ عموديا؟ ما هي السرعة القصوى التي ستكسبها مع الأجنحة وبدونها؟• ما مدى سرعة تحرك الطوارئ أفقيًا بحيث تطير لأعلى بدلاً من النزول عند بدء الرحلة؟• هل يمكن أن تقفز الطوارئ ، وتهدف إلى الأسفل ، من أجل اكتساب المزيد من السرعة والذهاب لبعض الوقت في رحلة أفقية؟• هل يمكنك بناء نموذج محسن يأخذ في الاعتبار زاوية الهجوم؟ ربما يمكنك ذلك ، ولكن يبدو لي أن الطيران بسرعة منخفضة موضوع معقد إلى حد ما.