 إذا ذهبنا إلى تاريخ دراسة مسارات الطيران من الأرض إلى القمر ، فأنت بحاجة إلى العودة قبل قرن ونصف ، في عام 1865 ، عندما تم نشر رواية جول فيرن الجديدة "من الأرض إلى القمر بطريقة مباشرة في 97 ساعة و 20 دقيقة". بالطبع ، كان هذا بعيدًا عن الكتاب الأول الذي وصف مثل هذه الرحلة ، لكنها كانت الرواية الأولى التي قرر المؤلف فيها تناول وصف السفر من وجهة نظر علمية.علاوة على ذلك ، يتم الآن فهم مستوى إعداد هذا النص جيدًا بشكل خاص ، نظرًا لأنه للمرة الأولى لم يتم عرض السفر إلى الفضاء فحسب ، ولكن تم تحليل جميع الفروق الدقيقة ، أحيانًا صغيرة جدًا ، بالتفصيل. الآن يحبون أن ينتقدوا الرواية عن تلك الأخطاء التي ارتكبها المؤلف. ولكن مع هذا الحجم الكبير من العمل ، سيكون من المفاجئ إذا لم تكن هناك أخطاء على الإطلاق! والآن ليست أخطائه هي التي تدهشه أكثر ، ولكن ما كان على حق بشأنه. على سبيل المثال ، فكرة أنظمة تنقية الأكسجين على كل من قشرة كولومبيادا ومركبة سويوز الفضائية متشابهة جدًا. فقط جول فيرن لديه هيدروكسيد الصوديوم ، والآن يستخدم هيدروكسيد الليثيوم.
إذا ذهبنا إلى تاريخ دراسة مسارات الطيران من الأرض إلى القمر ، فأنت بحاجة إلى العودة قبل قرن ونصف ، في عام 1865 ، عندما تم نشر رواية جول فيرن الجديدة "من الأرض إلى القمر بطريقة مباشرة في 97 ساعة و 20 دقيقة". بالطبع ، كان هذا بعيدًا عن الكتاب الأول الذي وصف مثل هذه الرحلة ، لكنها كانت الرواية الأولى التي قرر المؤلف فيها تناول وصف السفر من وجهة نظر علمية.علاوة على ذلك ، يتم الآن فهم مستوى إعداد هذا النص جيدًا بشكل خاص ، نظرًا لأنه للمرة الأولى لم يتم عرض السفر إلى الفضاء فحسب ، ولكن تم تحليل جميع الفروق الدقيقة ، أحيانًا صغيرة جدًا ، بالتفصيل. الآن يحبون أن ينتقدوا الرواية عن تلك الأخطاء التي ارتكبها المؤلف. ولكن مع هذا الحجم الكبير من العمل ، سيكون من المفاجئ إذا لم تكن هناك أخطاء على الإطلاق! والآن ليست أخطائه هي التي تدهشه أكثر ، ولكن ما كان على حق بشأنه. على سبيل المثال ، فكرة أنظمة تنقية الأكسجين على كل من قشرة كولومبيادا ومركبة سويوز الفضائية متشابهة جدًا. فقط جول فيرن لديه هيدروكسيد الصوديوم ، والآن يستخدم هيدروكسيد الليثيوم. والأكثر إثارة للاهتمام هي اللحظات التي كان فيها على حق ، على الرغم من الافتراضات غير الصحيحة. على سبيل المثال ، انتقده بيرلمان لإعطائه بيانات خاطئة عن وقت الرحلة من الأرض إلى القمر وجعلها باسم الرواية. أجرى عالم الرياضيات حسابات أكثر دقة بالطريقة المحددة ، بعد أن حصل على رقم ترتيب ستة أيام ، يومين أكثر من الرواية. وحساباته ، في إطار هذه الطريقة ، كانت صحيحة بالفعل. في غضون أربعة أيام فقط ، من الممكن حقًا الطيران إلى القمر (في الواقع ، وصلت العديد من الأجهزة إلى القمر في هذا الوقت تقريبًا) ، ولكن في ستة أيام من المستحيل بالفعل. تم اختيار طريقة الحساب من قبل كاتب الخيال العلمي بشكل غير صحيح ، ولكن تبين أن الرقم صحيح!ومع ذلك ، على سبيل المثال ، بعد وقت قصير من إصدار رواية "حول القمر" ، شكك الكثيرون في إمكانية مثل هذا المسار لطيار قريب من القمر تحت تأثير قوى الجاذبية فقط. فقط في بداية القرن العشرين ، عند تقييم المدارات في أنظمة النجوم الثنائية ، كانت إمكانية وجود مثل هذه المدارات تظهر حقًا. إليكم ما كتبته المجلة الإنجليزية "المعرفة" في بداية القرن العشرين في مقال "علم الفلك لجول فيرن":«, . , . . , . , , . , , , . . . . , . , , , ».وبعبارة أخرى ، لم تكن المهام التي حاول Jules Verne حلها في ذلك الوقت في طليعة العلم فحسب - بل غالبًا ما كانت تطرح أسئلة لم يتمكن العلم بعد ذلك من الإجابة عليها.ومع ذلك ، يجب ألا ينسى المرء أنه لم يفعل كل هذا بمفرده. عند كتابة جميع كتبه ، حاول المؤلف التوجه إلى المتخصصين في أي مجال. وفقًا لمذكراته ، فإن حسابات الرحلة من الأرض إلى القمر قام بها ابن عمه هنري جارس (1815-1871) ، مدرس رياضيات في ثانوية نابليون (الآن ليسيوم هنري الرابع). بالمناسبة ، يمكنك هنا رؤية كتابه باللغة الفرنسية ، المخصص لكوزموجرافيا Leçons nouvelles de Cosmographie (1854). وكانت حساباته دقيقة للغاية. على سبيل المثال ، هنا ، وفقًا للبيانات الواردة في الكتاب ، قمت بحساب تاريخ البدء الدقيق لطاقم كولومبيادا.
والأكثر إثارة للاهتمام هي اللحظات التي كان فيها على حق ، على الرغم من الافتراضات غير الصحيحة. على سبيل المثال ، انتقده بيرلمان لإعطائه بيانات خاطئة عن وقت الرحلة من الأرض إلى القمر وجعلها باسم الرواية. أجرى عالم الرياضيات حسابات أكثر دقة بالطريقة المحددة ، بعد أن حصل على رقم ترتيب ستة أيام ، يومين أكثر من الرواية. وحساباته ، في إطار هذه الطريقة ، كانت صحيحة بالفعل. في غضون أربعة أيام فقط ، من الممكن حقًا الطيران إلى القمر (في الواقع ، وصلت العديد من الأجهزة إلى القمر في هذا الوقت تقريبًا) ، ولكن في ستة أيام من المستحيل بالفعل. تم اختيار طريقة الحساب من قبل كاتب الخيال العلمي بشكل غير صحيح ، ولكن تبين أن الرقم صحيح!ومع ذلك ، على سبيل المثال ، بعد وقت قصير من إصدار رواية "حول القمر" ، شكك الكثيرون في إمكانية مثل هذا المسار لطيار قريب من القمر تحت تأثير قوى الجاذبية فقط. فقط في بداية القرن العشرين ، عند تقييم المدارات في أنظمة النجوم الثنائية ، كانت إمكانية وجود مثل هذه المدارات تظهر حقًا. إليكم ما كتبته المجلة الإنجليزية "المعرفة" في بداية القرن العشرين في مقال "علم الفلك لجول فيرن":«, . , . . , . , , . , , , . . . . , . , , , ».وبعبارة أخرى ، لم تكن المهام التي حاول Jules Verne حلها في ذلك الوقت في طليعة العلم فحسب - بل غالبًا ما كانت تطرح أسئلة لم يتمكن العلم بعد ذلك من الإجابة عليها.ومع ذلك ، يجب ألا ينسى المرء أنه لم يفعل كل هذا بمفرده. عند كتابة جميع كتبه ، حاول المؤلف التوجه إلى المتخصصين في أي مجال. وفقًا لمذكراته ، فإن حسابات الرحلة من الأرض إلى القمر قام بها ابن عمه هنري جارس (1815-1871) ، مدرس رياضيات في ثانوية نابليون (الآن ليسيوم هنري الرابع). بالمناسبة ، يمكنك هنا رؤية كتابه باللغة الفرنسية ، المخصص لكوزموجرافيا Leçons nouvelles de Cosmographie (1854). وكانت حساباته دقيقة للغاية. على سبيل المثال ، هنا ، وفقًا للبيانات الواردة في الكتاب ، قمت بحساب تاريخ البدء الدقيق لطاقم كولومبيادا.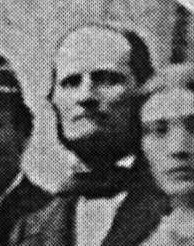 Henri Garcet (1815–1871)ومع ذلك ، ربما لم نكن لنتعرف على حساباته لو لم يكن جولز فيرن قد وضعها في بداية كتاب "حول القمر" ، باستخدامهم في محادثة طاقم قذيفة كولومبيادا. يكتبون أن قراء صحيفة "مناظرات" المؤرخة في 7 نوفمبر 1869 قد دهشوا حرفيا لرؤية الحسابات الرياضية المعقدة - بدأ نشر الرواية في هذه الصحيفة.هكذا تم وصف النموذج الرياضي للرحلة من خلال شفتي ميشال اردان وباربيكان:"هل تعلم يا باربيكان ، ما الذي كنت أفكر فيه طوال الليل؟"
Henri Garcet (1815–1871)ومع ذلك ، ربما لم نكن لنتعرف على حساباته لو لم يكن جولز فيرن قد وضعها في بداية كتاب "حول القمر" ، باستخدامهم في محادثة طاقم قذيفة كولومبيادا. يكتبون أن قراء صحيفة "مناظرات" المؤرخة في 7 نوفمبر 1869 قد دهشوا حرفيا لرؤية الحسابات الرياضية المعقدة - بدأ نشر الرواية في هذه الصحيفة.هكذا تم وصف النموذج الرياضي للرحلة من خلال شفتي ميشال اردان وباربيكان:"هل تعلم يا باربيكان ، ما الذي كنت أفكر فيه طوال الليل؟"
- ماذا عن؟ سأل الرئيس.
— . , , , . : , , , .
— , — , — , , , , , .
— , , — .- - ?
— .
— ?
…
"نعم يا صديقي العزيز". مع مراعاة جميع الظروف المعروفة للمشكلة:
المسافة من مركز الأرض إلى مركز القمر ، ونصف قطر الأرض ، وكتلة الأرض ، وكتلة القمر ، يمكنني تحديد السرعة الأولية لمقذفتنا بدقة ، وفي نفس الوقت باستخدام أبسط صيغة.
- ما هي الصيغة؟
- ولكن ترى. لكن فقط لن أشطب المنحنى الذي وصفته قوقعتنا بين القمر والأرض ، نظرًا لحركتها النسبية حول الشمس. لنفترض أن كلا الكوكبين بلا حراك. هذا سيكون كافيا
- لماذا؟
- لأن هذه هي الطريقة التي يتم بها حل المهام المسماة "المهام الثلاثية الجسم" ، فإن الطريقة المتكاملة لحل هذه المشاكل لم يتم تطويرها بشكل كافٍ بعد.بعد فترة ، تم تقديم الصيغة أيضًا ، والتي تم تقديمها للقراء:حيث r هو نصف قطر الأرض ، هي المسافة بين مركزي الأرض والقمر ، x هي مسافة القلب عن الأرض. V 0 هي السرعة الأولية للنواة. V هي السرعة على مسافة س.وبدت الرحلة على هذا النحوهنا أود أن أشير إلى أن هذه الصيغة مع البيانات الأولية المشار إليها صحيحة بالفعل. وهو يعرض بدقة تأثير الجاذبية للأرض والقمر على الجهاز في أي وقت. من السهل جدًا اشتقاق قانون الحفاظ على الطاقة.اشتقاق صيغة Verne-Garce
mv2 / 2 – γMm/R – γMm/R =const
m M,M – , ,
γ – , R - , R-
. .
mv2 / 2 – γMm/x– γMm/(D-x) =mv02 / 2 – γMm/r – γMm/(d-r)
m,
v2 / 2 –v02 / 2=γM/x+ γM/(D-x)– γM/r – γM/(d-r)
1/2*(v2-v02 )=γM(1/-1/r+M/M*1/(d-x)-M/M*1/(d-r))
1/2*(v2-v02 )=γM/r(r/-1+M/M(r/(d-x)-r/(d-r))
mg=mγM/r2 γM=g*r2
1/2*(v2-v02 )=gr(r/-1+M/M(r/(d-x)-r/(d-r))
إذن ما هي الصفقة؟ المشكلة هي أنه لا يأخذ في الاعتبار ديناميكيات النظام. يدور القمر حول الأرض بسرعة حوالي 1 كم / ثانية. هذه هي بالتحديد مشكلة هذه المشكلة. ونتيجة لذلك ، عند محاولة الطيران وفقًا للمخطط أعلاه ، عندما تطير المحطة إلى نقطة محايدة بين الأرض والقمر ، فلن يتم التقاطها على الإطلاق بواسطة حقل القمر ، نظرًا لأن هذا الأخير سيطير بعيدًا عن المقذوف بسرعة كيلومتر واحد في الثانية ، وستبدأ القذيفة في السقوط على الأرض. ولكن بعد ذلك كان هناك أمل في أن يتم التقاط الجهاز بواسطة القمر ، ومع ذلك ، فإن مخططًا مشابهًا لتقريب أول يوضح بدقة ديناميكيات الرحلة. مع اليد الخفيفة لجول فيرن ، سرعان ما أصبحت طريقة مماثلة لحساب الرحلة شائعة جدًا. بدأ استخدامه ليس فقط في كتب الفن ، ولكن أيضًا في الأعمال العلمية الجادة.وتجدر الإشارة إلى أن علماء الفلك فهموا بعد ذلك أهمية أخذ الديناميات في الاعتبار. نعم ، والمعادلات التفاضلية التي تأخذ في الاعتبار كلا من الجاذبية والديناميكيات ، يمكن بسهولة تكوينها. فقط لا يمكن العثور على حل بسيط. في الواقع ، كما هو مفهوم الآن جيدًا ، لا تحتوي مشكلة الأجسام الثلاثة على حل تحليلي عام.يمكن حل المشكلة عدديًا فقط ، مما يعني عددًا كبيرًا جدًا من الحسابات الروتينية ، والتي يمكن أن تقضي أشهرًا أو حتى سنوات من الحياة. في وقت نشر الرواية ، تم حل مشكلة مماثلة عدديًا مرتين فقط. علاوة على ذلك ، كانت المحاولة الأولى أكثر من مائة عام قبل نشر الرواية ، في 1759.من المعروف أن إدموند هالي ، الذي قام بتجميع كتالوج للمذنبات ، لاحظ أن العديد من المذنبات التي ظهرت في السماء في أوقات مختلفة لها معلمات متشابهة جدًا. بعد التحقق منها ، قرر أنه يمكن أن يكون نفس المذنب. ثم سيتم استدعاؤها باسمه. ظهر المذنب هالي في السماء في 1531 و 1607 و 1682. أي أن فترة التداول كانت 75-76 سنة ، وتنبأ العالم بالمظهر التالي لعام 1758. وكل شيء سيكون رائعًا ، إن لم يكن لـ "واحد": في الوقت المقدر ، لم يظهر المذنب في السماء أبدًا.ثم قرر عالم الرياضيات الفرنسي كليو حساب مسارها بأكبر قدر ممكن من الدقة. بما في ذلك ، مع مراعاة الاضطرابات في مسارها بسبب جاذبية المشتري وزحل. لقد كان عملًا متعبًا وطويلًا للغاية ، على الرغم من أنه لم يقم بهذا العمل بمفرده: فقد ساعده عالم الفلك ج. لالاند وعالم الرياضيات مدام ليبوت. اتضح أن الفرق مع التقديرات السابقة لفترة ثورة المذنب هو 618 يومًا ، وسيصل إلى الحضيض في 13 أبريل 1759. مع خطأ محتمل لمدة شهر. تبين أن التقييم كان دقيقًا جدًا: تجاوز المذنب مرحلة الحضيض في 12 مارس. كان انتصارًا لعلماء الرياضيات وتأكيدًا جيدًا لقوانين نيوتن.حول هذا الحساب ، كتب لالاند لاحقًا:حسبنا ستة أشهر من الصباح حتى الليل ، وأحيانًا دون النظر حتى من الطعام ، وكانت النتيجة أنني أزعجت صحتي لبقية أيام حياتي. كانت المساعدة التي قدمتها مدام ليبوت إلى درجة أنه بدونها لن نتجرأ أبدًا على القيام بهذا العمل الضخم ، الذي تألف من حساب مسافة المذنب من كوكبين - المشتري وزحل - لكل درجة من الكرة السماوية لمدة 150 عامًا. "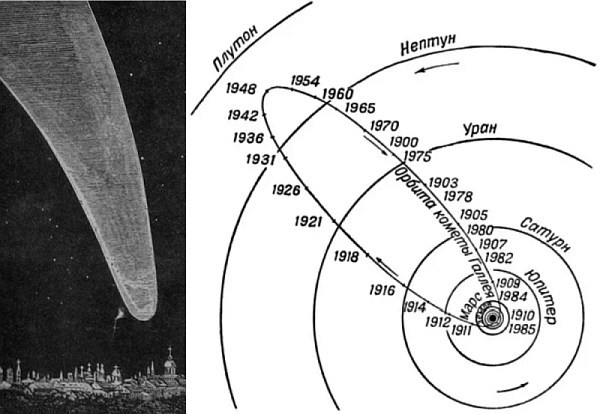 يمكنك رؤية مسار مذنب هالي بالنسبة إلى المدارات الكواكب فيالمرة الثانية التي استخدمت فيها طريقة مشابهة عام 1829 ، مرة أخرى عند حساب مسار مذنب هالي. أعطت التقديرات تاريخ عودة المذنب إلى الشمس في 15 نوفمبر 1835. عاد المذنب في 16 نوفمبر ، متأخرا بيوم واحد فقط.ونتيجة لذلك ، أثبتت طريقة رقمية مماثلة دقتها. ولكن من القصة المذكورة أعلاه ، يمكنك أن ترى بوضوح كم كان العمل الشاق المطلوب مملاً. استغرق ستة أشهر من عمل ثلاثة علماء رياضيات لحساب مسار واحد فقط مع معلمات أولية معروفة! ولكن لحساب مسارات رحلة طيران من الأرض إلى القمر ، كان من الضروري تقييم العشرات ، إن لم يكن المئات من المسارات ، مع معلمات أولية مختلفة. خلاف ذلك ، من المستحيل ، على سبيل المثال ، الحصول على السرعة الدقيقة ، وتاريخ الإطلاق ، وخصائص المسار ، والأخطاء المحتملة ، ومعلمات الطيران للمحطة بالقرب من القمر ، وما إلى ذلك. قد يستغرق ذلك سنوات من العمر. أي أن هذا الحل اعتبر صعبًا للغاية. خاصة بالنسبة لمهمة ليس لها معنى عملي كبير.في الوقت نفسه ، كانت هناك أيضًا ثقة في أنه يمكن العثور على حل تحليلي لمشكلة الأجسام الثلاثة. السماح ، على الأقل في تقدير تقريبي ، بتقييم معلمات الرحلة.وبدا أن الطريقة التي اقترحها جول فيرن تعطي إجابة على هذا السؤال. بعد كل شيء ، من الناحية الرياضية ، في إطار الافتراضات الأولية ، كان لا تشوبه شائبة. نعم ، لم يأخذ في الاعتبار الديناميكيات ، ولكن بعد ذلك توقع الكثيرون أن هذا الافتراض كان طبيعيًا ، وسيبدو المسار الحقيقي للقذيفة من الأرض إلى القمر شيئًا مثل هذا.الحساب من كتاب "سفن الفضاء". (الاتصالات بين الكواكب في أوهام الروائيين) "1928، والجمال الرياضي ، إلى جانب الشعبية العظيمة للرواية ، لعب نكتة قاسية: باستخدام هذه الطريقة ، عمليا جميع رواد استكشاف الفضاء - جودارد ، ستيرنفلد ، أوبرت ، ماكس فالي والعديد من الآخرين - تم تقييم الرحلة . في بعض الأحيان ، نادرًا جدًا ، لم يقدروا أيضًا رحلة طيران مباشرة ، ولكن بواسطة القطع الناقص للقمر الصناعي للأرض. ولكن هذه الطريقة لها أيضًا عيوبها. على سبيل المثال ، لسبب ما كان الكثيرون على يقين من أنه للوصول إلى القمر كان كافياً أن يقع في مجال عمله. علاوة على ذلك ، كما يقولون ، يجب أن يقوم جاذبية القمر بالباقي. على الرغم من أنه ، كما قيل أعلاه ، فقد ثبت بالفعل إمكانية التحليق في مشكلة الأجسام الثلاثة.من الأمثلة الجيدة على ذلك مقال فيرنر فون براون في الجريدة الأسبوعية في 18 أكتوبر 1952 ، حيث وصف فون براون كيف ، في رأيه ، كيف ستبدو البعثة إلى القمر.
يمكنك رؤية مسار مذنب هالي بالنسبة إلى المدارات الكواكب فيالمرة الثانية التي استخدمت فيها طريقة مشابهة عام 1829 ، مرة أخرى عند حساب مسار مذنب هالي. أعطت التقديرات تاريخ عودة المذنب إلى الشمس في 15 نوفمبر 1835. عاد المذنب في 16 نوفمبر ، متأخرا بيوم واحد فقط.ونتيجة لذلك ، أثبتت طريقة رقمية مماثلة دقتها. ولكن من القصة المذكورة أعلاه ، يمكنك أن ترى بوضوح كم كان العمل الشاق المطلوب مملاً. استغرق ستة أشهر من عمل ثلاثة علماء رياضيات لحساب مسار واحد فقط مع معلمات أولية معروفة! ولكن لحساب مسارات رحلة طيران من الأرض إلى القمر ، كان من الضروري تقييم العشرات ، إن لم يكن المئات من المسارات ، مع معلمات أولية مختلفة. خلاف ذلك ، من المستحيل ، على سبيل المثال ، الحصول على السرعة الدقيقة ، وتاريخ الإطلاق ، وخصائص المسار ، والأخطاء المحتملة ، ومعلمات الطيران للمحطة بالقرب من القمر ، وما إلى ذلك. قد يستغرق ذلك سنوات من العمر. أي أن هذا الحل اعتبر صعبًا للغاية. خاصة بالنسبة لمهمة ليس لها معنى عملي كبير.في الوقت نفسه ، كانت هناك أيضًا ثقة في أنه يمكن العثور على حل تحليلي لمشكلة الأجسام الثلاثة. السماح ، على الأقل في تقدير تقريبي ، بتقييم معلمات الرحلة.وبدا أن الطريقة التي اقترحها جول فيرن تعطي إجابة على هذا السؤال. بعد كل شيء ، من الناحية الرياضية ، في إطار الافتراضات الأولية ، كان لا تشوبه شائبة. نعم ، لم يأخذ في الاعتبار الديناميكيات ، ولكن بعد ذلك توقع الكثيرون أن هذا الافتراض كان طبيعيًا ، وسيبدو المسار الحقيقي للقذيفة من الأرض إلى القمر شيئًا مثل هذا.الحساب من كتاب "سفن الفضاء". (الاتصالات بين الكواكب في أوهام الروائيين) "1928، والجمال الرياضي ، إلى جانب الشعبية العظيمة للرواية ، لعب نكتة قاسية: باستخدام هذه الطريقة ، عمليا جميع رواد استكشاف الفضاء - جودارد ، ستيرنفلد ، أوبرت ، ماكس فالي والعديد من الآخرين - تم تقييم الرحلة . في بعض الأحيان ، نادرًا جدًا ، لم يقدروا أيضًا رحلة طيران مباشرة ، ولكن بواسطة القطع الناقص للقمر الصناعي للأرض. ولكن هذه الطريقة لها أيضًا عيوبها. على سبيل المثال ، لسبب ما كان الكثيرون على يقين من أنه للوصول إلى القمر كان كافياً أن يقع في مجال عمله. علاوة على ذلك ، كما يقولون ، يجب أن يقوم جاذبية القمر بالباقي. على الرغم من أنه ، كما قيل أعلاه ، فقد ثبت بالفعل إمكانية التحليق في مشكلة الأجسام الثلاثة.من الأمثلة الجيدة على ذلك مقال فيرنر فون براون في الجريدة الأسبوعية في 18 أكتوبر 1952 ، حيث وصف فون براون كيف ، في رأيه ، كيف ستبدو البعثة إلى القمر.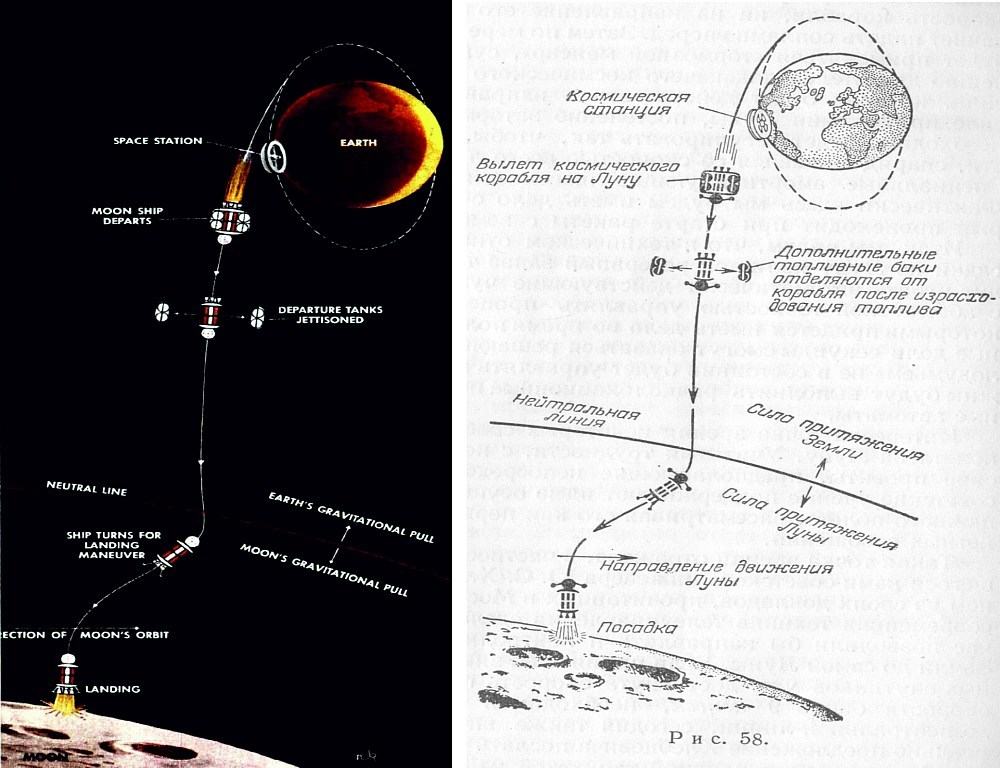
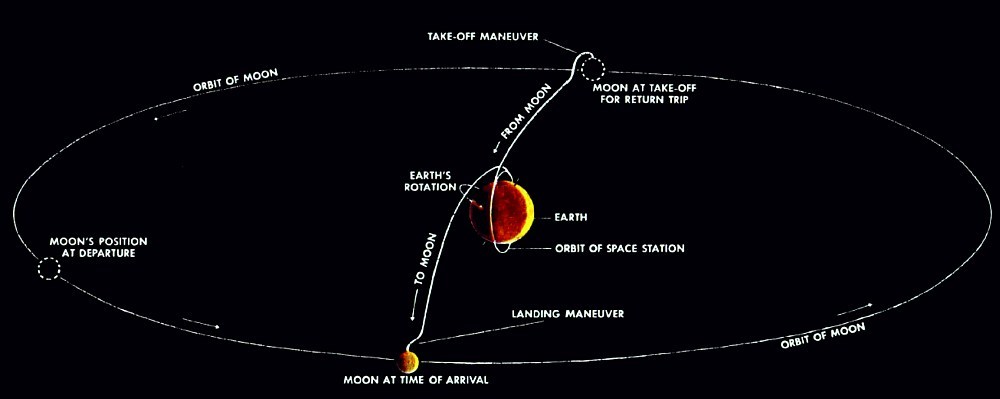 يمكن تنزيل المقالة نفسها هنا.من الرسم التوضيحي ، من الواضح أنه من الواضح أنه مخطط جول فيرن الذي يتم تقديمه هناك: أولاً ، الوصول إلى منطقة محايدة بين الأرض والقمر ، ومن ثم الوقوع على القمر تحت تأثير جاذبيتها. تم استبدال المدفع بصاروخ منذ فترة طويلة ، لكن المبدأ الأساسي لم يتغير. على الرغم من مرور حوالي مائة عام على نشر الرواية.ولكن سرعان ما بدأ نهج الرحلات من الأرض إلى القمر يتغير. بما في ذلك بفضل تطوير أجهزة الكمبيوتر الإلكترونية.استمرار التالي .
يمكن تنزيل المقالة نفسها هنا.من الرسم التوضيحي ، من الواضح أنه من الواضح أنه مخطط جول فيرن الذي يتم تقديمه هناك: أولاً ، الوصول إلى منطقة محايدة بين الأرض والقمر ، ومن ثم الوقوع على القمر تحت تأثير جاذبيتها. تم استبدال المدفع بصاروخ منذ فترة طويلة ، لكن المبدأ الأساسي لم يتغير. على الرغم من مرور حوالي مائة عام على نشر الرواية.ولكن سرعان ما بدأ نهج الرحلات من الأرض إلى القمر يتغير. بما في ذلك بفضل تطوير أجهزة الكمبيوتر الإلكترونية.استمرار التالي .