في شهر نوفمبر ، حيرت مجلة Quanta قراءها بأسئلة حول رسم الأشكال من الأشياء المسطحة المتطابقة (مثل العملات المعدنية أو الدومينو). تقدم هذه المقالة أسئلة وأجوبة مفصلة لهم.السؤال 1
, , . . . , , ? n ?
جسديًا ، تتطلب المهمة موازنة عزم الدوران على جانبي حافة الطاولة. عزم كل جانب هو نتاج كتلة هذا الجانب والمسافة من مركز الكتلة إلى الحافة. عندما يكون مركز كتلة الشكل بأكمله فوق الحافة ، تعمل نفس اللحظة على كلا الجانبين ، ويكون عزم دوران النظام الإجمالي صفرًا. بالنسبة للعنصر المركب ، يمكن العثور على عزم الدوران الإجمالي لأي وجه عن طريق إضافة عزم الدوران لجميع المكونات. لذلك ، يمكننا تقسيم المهمة الأصلية والتحكم فيها ، مع مراعاة التغييرات التي تحدث فقط عند إضافة كتلة جديدة إلى مكدس موجود ، وهو ما يشبه الاستقراء الرياضي (دعنا نسميها الاستقراء المادي).ضع في اعتبارك مجموعة من كتل n-1 ، يزن كل منها وحدة واحدة من الوزن ويبلغ طولها وحدة واحدة من الطول. المكدس متوازن عند حافة الطاولة. تخيل أن خط الرؤية موجه على طول حافة الطاولة ، والطاولة على اليسار - أي أن النهايات المعلقة من الكتل تبرز إلى اليمين. بما أن المكدس متوازن عند الحافة ، فإن مركز الكتلة يقع مباشرة فوق الحافة ، وعزمه صفر. تخيل الآن أننا قمنا برفع المكدس بالكامل عموديًا ، ووضعنا كتلة أخرى تحته بحيث تكون الحافة اليمنى متدفقة مع حافة الطاولة. من الناحية العملية ، قد يكون هذا صعبًا ، ولكن في تجربة فكرية يكون الأمر بسيطًا.أضفنا بعض الثبات إلى المكدس بإضافة الكتلة n من الأسفل ، لأن مركز كتلة المكدس بأكمله تحول قليلاً إلى اليسار. تدل على هذا الإزاحة س. كتل n تزن وحدات n ، ولها عزم دوران مشترك x * n حول حافة الطاولة ، موجه إلى اليسار. تذكر أن مجموعة كتل n-1 لها لحظة صفرية إجمالية. أضفنا فقط لحظة الكتلة الجديدة - بكتلة وحدة واحدة من الكتلة ومسافة إلى مركز الكتلة من حافة الطاولة بنصف وحدة طول.اتضح أن x * n = 1/2 ، مما يعني x = 1 / 2n ، حيث x هي المسافة إلى مركز الكتلة الجديد من حافة الجدول.هذا يعني أنه إذا قمت بتحريك مجموعة الكتل n بالكامل إلى اليمين بمقدار 1/2 في الطول ، فستكون متوازنة تمامًا عند الحافة - وهذا هو أقصى تحول ممكن. لإكمال بناء الحث ، نلاحظ أن الحد الأقصى للكتلة الأولى من حافة الجدول هو 1/2 وحدة طول.لذلك ، بالنسبة إلى خمس كتل ، نستبدل في الصيغة n لكل مستوى من 1 إلى 5 للحصول على الحد الأقصى من التراكب:x=1/2+1/4+1/6+1/8+1/10=137/120=1,141(6)
يمكن ملاحظة أنه إذا بدأت من الأعلى ثم أضفت كتلًا لأسفل ، فستكون كل نقلة نصف التبادلي لعدد الكتل المتاحة. تُعرف هذه التسلسلات من الأرقام المعكوسة باسم السلسلة التوافقية. تتباعد هذه السلسلة ببطء ، وبما أن n تميل إلى اللانهاية ، فإنها تميل أيضًا إلى اللانهاية.يتم الحصول على صيغة المجموع العام للكتل n عن طريق جمع جميع أعضاء السلسلة. اتضح نصف المصطلح التوافقي التاسع ، والذي يمكن كتابته على النحو التالي:السؤال 2
تخيل أن لديك نفس الكتل الخمس ، وتريد وضع بعض الزخارف على أعلىها ، في نقطة تبلغ ربع طول الكتلة من الطرف المعلق. تزن جميع الكتل وحدة واحدة من الوزن ، وتزن المجوهرات خمس الكتلة. ما هو الحد الأقصى لطول البروز الآن؟ كيف يغير هذا الصيغة الأساسية؟
أولاً ، ضع في اعتبارك الكتلة الأولى مع الزخرفة الواضحة عليها ، والاستلقاء بحيث تكون الحافة اليمنى متدفقة مع حافة الطاولة. يبلغ مركز كتلة الكتلة بدون زخرفة نصف وحدة طول من حافة الطاولة. ستنقل الزخرفة إلى اليمين ، على سبيل المثال ، بعلامة x. كتلة الزخرفة هي 1/5 ، وستكون المسافة من المركز الجديد للكتلة 1/4. نحن نساوي اللحظات ونحصل على س = 1/5 * (1/4 س) ، وبالتالي ، س = 1/24. بسبب الزخرفة ، من الضروري تحريك الكتلة الأولى إلى اليسار بمقدار 1/24 من الطول ، بحيث يكون الحد الأقصى للتراكب الآن 11/24 بدلاً من 1/2.بالنسبة للكتل اللاحقة ، يمكن استخدام نفس الحث كما في السؤال الأول. نحصل على المعادلة x (n + 1/5) = 1/2 ، والتي يتم تبسيطها لكتل n إلى 1/2 (n + 1/5). هذا يعطينا التسلسل 1/24 + 5/12 + 5/22 + 5/32 + 5/42 ... ، مما يؤدي إلى الحد الأقصى من المتراكمة 1،057 لشكل من خمسة مستويات. لاحظ أن عبء الكتلة الأولى لا يتناسب مع المخطط العام بسبب الوزن الإضافي للزخرفة. ومع ذلك ، يظهر تسلسل توافقي بسيط يمكن من خلاله حساب الكمية النهائية بسهولة.السؤال 3
, , . . . , . , , . , ?
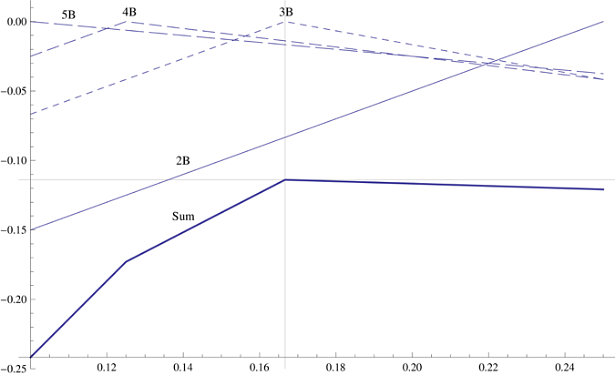
نظرًا لأن احتمال وجود كتلتين إلى خمس كتل هو نفسه ، فأنت بحاجة إلى زيادة المبلغ الذي يشير إلى الحد الأقصى من التراكب لهذه الحالات الأربع. بالنسبة لمكدس مكون من 2-5 كتل ، يوجد الموضع الأمثل للكتلة الأولى ، مما يمنح أقصى عبء للمكدس بأكمله. إذا قمت ببناء أكبر عبء على الرسم البياني لكل من الأحجام الأربعة المحتملة للمكدس التالي ، فستحصل على رسمين بيانيين خطيين ورسامين بيانيين على شكل حرف V مقلوب. تشير رؤوسهم إلى موضع البدء الأمثل للكتلة الأولية للمكدسات المكونة من 3-4 كتل. تلخيص الرسوم البيانية ، نحصل على الرسم البياني الإجمالي المتدلي ، والذي يغير الاتجاه بشكل كبير في كل من المواضع المثلى الأربعة. اتضح أن أفضل عبء عام يتم تحقيقه في الموضع الأمثل للكتل الثلاث ، وبعد ذلك ينخفض الرسم البياني. لذلك ، تحتاج إلى وضع الكتلة الأصلية تحت الافتراضأنه سيتم إعطاؤك ثلاث كتل إضافية ، وستكون البروز 1/6 وحدات طول.