قبل 70 عامًا ، في 16 ديسمبر 1947 ، في مختبرات Bell Labs ، أنشأ جون باردين ووالتر براتين ، تحت إشراف وليام شوكلي ، أول ترانزستور ثنائي القطب التشغيلي. في 23 ديسمبر ، أظهر براتين لزملائه أول مكبر للصوت الترانزستور. لذلك ، غالبًا ما يسمى هذا اليوم بيوم الترانزستور . ليست هناك حاجة للحديث عن أهمية هذا الحدث. يعتبر الترانزستور أحد أهم الاختراعات في القرن العشرين ، والتي بدونها ستظل أجهزة الكمبيوتر تعمل على المصابيح والمرحلات ، وتحتل مباني كاملة. حصل شوكلي وباردين وبراتين على جائزة نوبل في الفيزياء لعملهم في عام 1956. على مر السنين ، تم تصغير الترانزستور إلى عدد قليل من الذرات. يحتوي كل معالج على مليارات الترانزستورات ، لذلك يمكن تسمية الترانزستور بأكبر جهاز تم إنشاؤه من قبل البشرية.ولكن ما هو نوع العمل الذي يقوم به الترانزستور لنا؟ دعنا نذهب في رحلة ذهنية: سنتتبع المسار من بعض أطراف الأصابع عالية المستوى إلى عيد ميلادنا - الترانزستور.ما يجب أن تتخذ كنقطة انطلاق؟ حسنًا ، على الأقل ارسم زر حبركت.
ليست هناك حاجة للحديث عن أهمية هذا الحدث. يعتبر الترانزستور أحد أهم الاختراعات في القرن العشرين ، والتي بدونها ستظل أجهزة الكمبيوتر تعمل على المصابيح والمرحلات ، وتحتل مباني كاملة. حصل شوكلي وباردين وبراتين على جائزة نوبل في الفيزياء لعملهم في عام 1956. على مر السنين ، تم تصغير الترانزستور إلى عدد قليل من الذرات. يحتوي كل معالج على مليارات الترانزستورات ، لذلك يمكن تسمية الترانزستور بأكبر جهاز تم إنشاؤه من قبل البشرية.ولكن ما هو نوع العمل الذي يقوم به الترانزستور لنا؟ دعنا نذهب في رحلة ذهنية: سنتتبع المسار من بعض أطراف الأصابع عالية المستوى إلى عيد ميلادنا - الترانزستور.ما يجب أن تتخذ كنقطة انطلاق؟ حسنًا ، على الأقل ارسم زر حبركت.HTML و CSS
يتكون الزر من بكسل الخلفية والنص والحدود. في الكود ، تم تعيينه بواسطة علامة <a> ، التي يتم تطبيق قواعد تخطيط CSS عليها. على سبيل المثال ، يتم تطبيق قاعدة CSS على حد على الزوايا المستديرة:border-radius: 3px;
 وبالتالي ، يتكون الحد من أربعة أجزاء وأربعة أقواس ("أرباع" دائرة).
وبالتالي ، يتكون الحد من أربعة أجزاء وأربعة أقواس ("أرباع" دائرة).متصفح
للبحث ، أخذت فايرفوكس المفضلة لدي. قبل أن يبدأ FF في رسم زرنا ، يحتاج إلى القيام بالكثير من العمل على التحليل وحساب موضع العناصر:- تنزيل HTML عبر شبكة ، تحليل ، إنشاء شجرة DOM
- قم بالتنزيل عبر شبكة CSS ، قم بإجراء تحليل معجمي ، تحليل
- ربط القواعد بناءً على الأولوية والوراثة لعناصر الصفحة
- لجميع العقد DOM المرئية ، قم بتكوين شجرة مناطقها المستطيلة - الإطارات.
- للإطارات ، احسب الأبعاد والموقع (انظر الفيديو )
- قم بتكوين طبقات من الإطارات مع مراعاة فهرس z ونوع المحتوى (<canvas> ، SVG ، <video>).
- إنشاء قائمة رسم بالترتيب: لون الخلفية ، صورة الخلفية ، الحدود ، الأحفاد ، المخطط التفصيلي.
لن نتناول هذه الخطوات بالتفصيل. بعد ذلك يأتي الرسم الفعلي للعناصر الضرورية.ملف nsCSSRenderingBorders.cpp مسؤول عن رسم الحدود . والوظيفة العامة لرسم الحدود تسمى (من كان يظن): DrawBorders () . تحدد الوظيفة طريقة العرض المثلى لمختلف المواقف. لدينا حالة بسيطة نسبيًا: هناك نصف قطر حد ، ولكن الحدود من جميع الجوانب صلبة ومن نفس اللون.إذا لديناif (allBordersSame &&
mCompositeColors[0] == nullptr &&
mBorderStyles[0] == NS_STYLE_BORDER_STYLE_SOLID &&
!mAvoidStroke &&
!mNoBorderRadius)
{
gfxRect outerRect = ThebesRect(mOuterRect);
RoundedRect borderInnerRect(outerRect, mBorderRadii);
borderInnerRect.Deflate(mBorderWidths[eSideTop],
mBorderWidths[eSideBottom],
mBorderWidths[eSideLeft],
mBorderWidths[eSideRight]);
RefPtr<PathBuilder> builder = mDrawTarget->CreatePathBuilder();
AppendRoundedRectToPath(builder, mOuterRect, mBorderRadii, true);
AppendRoundedRectToPath(builder, ToRect(borderInnerRect.rect), borderInnerRect.corners, false);
RefPtr<Path> path = builder->Finish();
mDrawTarget->Fill(path, color);
return;
}
هناك خيارات أكثر تعقيدًا ، مثل الإرساء في زوايا ذات نصف قطر حد لأنواع مختلفة من الحدود المنقطة والمتقطعة ، راجع DrawDashedOrDottedCorner () . هناك في التعليمات البرمجية بالكاملولكن مرة أخرى إلى لو لدينا. نتعلم من التعليق أنه في هذه الحالة يتم رسم الحدود باستخدام مستطيلين - داخلي وخارجي ، ثم يتم ملء المسار (المسار) باللون المطلوب.AppendRoundedRectToPath(builder, mOuterRect, mBorderRadii, true);
AppendRoundedRectToPath(builder, ToRect(borderInnerRect.rect), borderInnerRect.corners, false);
RefPtr<Path> path = builder->Finish();
mDrawTarget->Fill(path, color);
انتقل إلى AppendRoundedRectToPath () في gfx / 2d / PathHelpers.cpp.نتعلم من التعليق على الوظيفة أن الزوايا مرسومة عند أربع نقاط تحكم بواسطة منحنيات بيزييه . غالبًا ما تُستخدم منحنيات Bezier في رسومات الكمبيوتر ، بما في ذلك لرسم أقواس الدوائر والعلامات الحذف. بينما نتعلم أكثر من التعليق ، هناك العديد من الخيارات لاختيار نقاط التحكم لبناء منحنى. في هذه الحالة ، نحتاج إلى أن النقاط 0 و 3 تنتمي إلى جانبي المستطيل ، والنقاط 0 ، 1 و C تقع على خط مستقيم واحد ، والنقاط 3 و 2 و C من جهة أخرى. انظر الشكل: يبقى لنا أن نحسب نسبة أطوال المقاطع 01 / 0C و 32 / 3C. هنا يستخدم المؤلفون حسابات تقريبية ويحصلون على ثابت ألفا السحري:
يبقى لنا أن نحسب نسبة أطوال المقاطع 01 / 0C و 32 / 3C. هنا يستخدم المؤلفون حسابات تقريبية ويحصلون على ثابت ألفا السحري:const Float alpha = Float(0.55191497064665766025);
لسوء الحظ ، فإن المقالات التي تحتوي على خوارزمية اختيار نقطة التحقق المشار إليها بواسطة التعليق ليست في المجال العام. ولكن بشكل عام ، تجدر الإشارة إلى أنه في رسومات الكمبيوتر ، غالبًا ما تستخدم الخوارزميات تقريبًا لتحسين الأداء. على سبيل المثال ، تسمح لك خوارزمية Brezenham برسم أجزاء ودوائر ليس "في الجبهة" - عن طريق حل المعادلات y = f (x) ، ولكن مع المزيد من العمليات الصحيحة الماكرة. نفس الشيء مع التعبئة ، إلخ.علاوة على ذلك ، في الدورة ، ننتقل من الزاوية إلى الزاوية ، نستخدم ألفا لحساب إحداثيات نقاط التحكم ، وأخيرًا ، استدعاء وظائف رسم خط الحدود وقوس الزاوية:aPathBuilder->LineTo(p0);
aPathBuilder->BezierTo(p1, p2, p3);
كود AppendRoundedRectToPath () الكاملvoid
AppendRoundedRectToPath(PathBuilder* aPathBuilder,
const Rect& aRect,
const RectCornerRadii& aRadii,
bool aDrawClockwise)
{
const Float alpha = Float(0.55191497064665766025);
typedef struct { Float a, b; } twoFloats;
twoFloats cwCornerMults[4] = { { -1, 0 },
{ 0, -1 },
{ +1, 0 },
{ 0, +1 } };
twoFloats ccwCornerMults[4] = { { +1, 0 },
{ 0, -1 },
{ -1, 0 },
{ 0, +1 } };
twoFloats *cornerMults = aDrawClockwise ? cwCornerMults : ccwCornerMults;
Point cornerCoords[] = { aRect.TopLeft(), aRect.TopRight(),
aRect.BottomRight(), aRect.BottomLeft() };
Point pc, p0, p1, p2, p3;
if (aDrawClockwise) {
aPathBuilder->MoveTo(Point(aRect.X() + aRadii[RectCorner::TopLeft].width,
aRect.Y()));
} else {
aPathBuilder->MoveTo(Point(aRect.X() + aRect.Width() - aRadii[RectCorner::TopRight].width,
aRect.Y()));
}
for (int i = 0; i < 4; ++i) {
int c = aDrawClockwise ? ((i+1) % 4) : ((4-i) % 4);
int i2 = (i+2) % 4;
int i3 = (i+3) % 4;
pc = cornerCoords[c];
if (aRadii[c].width > 0.0 && aRadii[c].height > 0.0) {
p0.x = pc.x + cornerMults[i].a * aRadii[c].width;
p0.y = pc.y + cornerMults[i].b * aRadii[c].height;
p3.x = pc.x + cornerMults[i3].a * aRadii[c].width;
p3.y = pc.y + cornerMults[i3].b * aRadii[c].height;
p1.x = p0.x + alpha * cornerMults[i2].a * aRadii[c].width;
p1.y = p0.y + alpha * cornerMults[i2].b * aRadii[c].height;
p2.x = p3.x - alpha * cornerMults[i3].a * aRadii[c].width;
p2.y = p3.y - alpha * cornerMults[i3].b * aRadii[c].height;
aPathBuilder->LineTo(p0);
aPathBuilder->BezierTo(p1, p2, p3);
} else {
aPathBuilder->LineTo(pc);
}
}
aPathBuilder->Close();
}
ولكن كل هذا يتوقف على الواجهة الخلفية للرسومات ثنائية الأبعاد التي تستخدمها Mozilla.محرك الرسومات
تستخدم Gecko مكتبة Moz2D المستقلة عن المنصة ، والتي بدورها يمكنها استخدام إحدى الخلفيات: القاهرة ، سكايا ، Direct2D ، كوارتز و NV Path. على سبيل المثال ، تتوفر Direct2D والقاهرة وسكيا لنظام التشغيل Windows. Skia هي أيضًا الواجهة الخلفية لـ Chromium. يمكنك تغيير الواجهة الخلفية حول: config. بدورها ، يمكن للواجهة الخلفية قراءة كل شيء على وحدة المعالجة المركزية ، أو يمكنهم استخدام تسريع أجهزة GPU إلى حد ما. على سبيل المثال ، تمتلك Skia الواجهة الخلفية OpenGL الخاصة بها - Ganesh.رمز Direct2D مغلق ، لذا من الأفضل تشغيل Skia ومعرفة ما يفعله. يتم استدعاء وظيفة رسم منحنى مكعب SkPath :: cubicTo. لبناء منحنى ، يتم تقسيمه بواسطة خوارزمية de Castelljo إلى عدد من الأجزاء المستقيمة ، والتي يتم رسمها بالفعل (انظر core / SkGeometry.cpp).كود الجهاز
لنكون صادقين ، لم أتمكن من فهم الأجزاء الداخلية لـ Skia بشكل كامل ، لذلك عدت خطوة إلى الوراء - إلى AppendRoundedRectToPath () ، حيث يتم تنفيذ جميع العمليات على الأعداد الصحيحة - والتي يمكن أن تكون أبسط؟بعد فتح الكود المفكك ، يجب أن نجد عملية الإضافة فيه....
142B1863 00 00 add byte ptr [eax],al
142B1865 00 8D 43 FF 0F 84 add byte ptr [ebp-7BF000BDh],cl
142B186B 67 01 00 add dword ptr [bx+si],eax
142B186E 00 99 0F 57 C9 F7 add byte ptr [ecx-836A8F1h],bl
142B1874 F9 stc
142B1875 8B C3 mov eax,ebx
142B1877 8B CA mov ecx,edx
142B1879 99 cdq
142B187A F7 7C 24 28 idiv eax,dword ptr [esp+28h]
...
أجل! حتى شخص بعيد عن ASM بقدر ما أستطيع أن أخمن بسهولة أن عملية ADD هي المسؤولة عن الإضافة. خذ العملية الأولى:142B1863 00 00 add byte ptr [eax],al0x142B1863 - العنوان في ذاكرة الوصول العشوائي0x00 - كود التشغيل - كود تعليمات المعالج. تم تجميع Mozilla تحت x86 ، وفتح جدول تعليمات x86 ، سنرى أن الرمز 00 يعني عملية إضافة 8 بت مع وسائل الاستذكار ADD. يمكن أن يكون المعامل الأول عبارة عن سجل أو خلية ذاكرة وصول عشوائي ، والثاني يمكن أن يكون تسجيلًا. يضاف المعامل الأول إلى الثاني ، وتكتب النتيجة إلى الأول. سأوضح ، فقط في حالة ، أن التسجيل عبارة عن ذاكرة RAM فائقة السرعة داخل المعالج ، على سبيل المثال ، لتخزين نتائج الحساب المتوسطة.البايت الثاني هو أيضًا 0x00 ويسمى MOD-REG-R / M. بتاتها تحدد المعاملات وطريقة العنونة. يعني MOD = 00b بالاشتراك مع R / M = 000b أنه يتم استخدام العنونة غير المباشرةREG = 000b يعني أن سجل AL يستخدم (الجزء السفلي من 8 بت من سجل EAX)[eax] - يشير إلى أن الإضافة تتم باستخدام خلية ذاكرة الوصول العشوائي ، عنوانه في سجل EAX ،كيف يعالج المعالج الأمر ADD؟
يعني MOD = 00b بالاشتراك مع R / M = 000b أنه يتم استخدام العنونة غير المباشرةREG = 000b يعني أن سجل AL يستخدم (الجزء السفلي من 8 بت من سجل EAX)[eax] - يشير إلى أن الإضافة تتم باستخدام خلية ذاكرة الوصول العشوائي ، عنوانه في سجل EAX ،كيف يعالج المعالج الأمر ADD؟وحدة المعالجة المركزية
استنادًا إلى وصف العمارة المصغرة Skylake ، قمت بتجميع قائمة (مبسطة للغاية) من الخطوات:- يتم جلب تعليمات X86 من ذاكرة التخزين المؤقت لتعليمات 32 كيلوبايت L1 إلى مخزن مؤقت للترميز 16 بايت
- يتم تنظيم الأوامر التي تم ترميزها مسبقًا في قائمة انتظار التعليمات (2x25 في الحجم) والدخول إلى أجهزة فك التشفير
- x86 1-4 (µOPs). ADD 1 µOP ALU (- ) 2 µOP AGU ( ) (., ). 86 .
- Allocation Queue (IDQ). , Loop Stream Detector — .
- : , . . .
- يذهب Microoperation إلى مدير الجدولة الموحدة ، الذي يقرر في أي نقطة وفي أي منفذ لإرسال العمليات للتنفيذ خارج ترتيب الاستلام. خلف كل منفذ يوجد مشغل. سوف تذهب عملياتنا الدقيقة إلى ALU و AGU.
 جوهر SkyLake. صورة من en.wikichip.org .أكرر ، هذا هو وصفي المبسط للغاية ولا يدعي أنه دقيق وكامل. لمزيد من المرجع ، أوصي بقراءة ما بعد الرحلة من خلال معالج المعالج الحاسوبي والمقالة المعالجات من عائلة Intel Core i7
جوهر SkyLake. صورة من en.wikichip.org .أكرر ، هذا هو وصفي المبسط للغاية ولا يدعي أنه دقيق وكامل. لمزيد من المرجع ، أوصي بقراءة ما بعد الرحلة من خلال معالج المعالج الحاسوبي والمقالة المعالجات من عائلة Intel Core i7ALU
الآن سيكون من المثير للاهتمام معرفة ما يحدث في ALU: كيف يتم جمع الأرقام؟ لسوء الحظ ، فإن المعلومات المتعلقة بالتنفيذ المحدد للهندسة المعمارية الدقيقة و ALU هي سر تجاري لشركة Intel ، لذلك ننتقل إلى النظرية لاحقًا.جهاز لإضافة بتين ثنائيتين (أي قليلا) يسمى adder . الإخراج هو المجموع وتحمل بت. المصدر: ويكيبيديامنذ في الحياة الواقعية ، نحتاج إلى إضافة أرقام تتكون من عدة أرقام ، كما يجب على المُقبل قبول البت الحامل من الرقم السابق كمدخل. ويسمى هذا الأفعام بالكامل .
المصدر: ويكيبيديامنذ في الحياة الواقعية ، نحتاج إلى إضافة أرقام تتكون من عدة أرقام ، كما يجب على المُقبل قبول البت الحامل من الرقم السابق كمدخل. ويسمى هذا الأفعام بالكامل .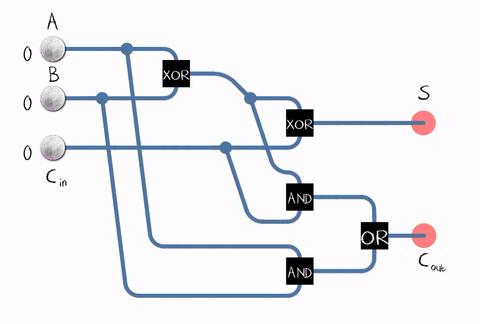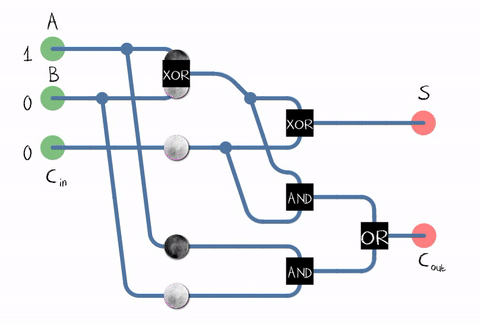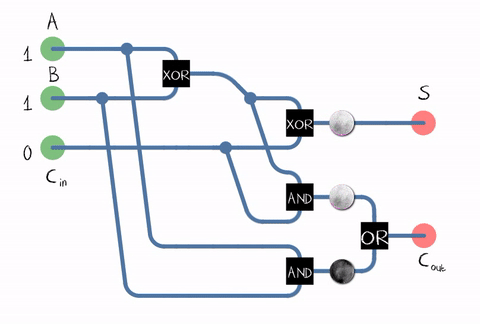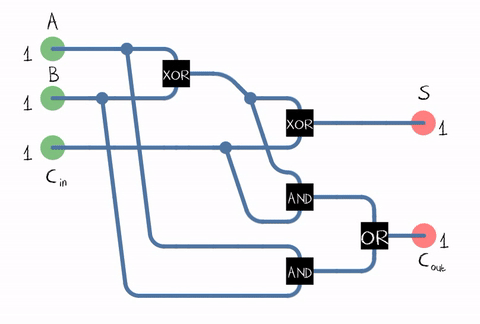 المصدر: ويكيبيدياكما يتضح من الشكل ، فإن المُصنّع يتألف من عناصر منطقية: XOR و AND و OR. وكل عنصر منطقييمكن تنفيذها باستخدام ترانزستورات متعددة. أو حتى تتابع .
المصدر: ويكيبيدياكما يتضح من الشكل ، فإن المُصنّع يتألف من عناصر منطقية: XOR و AND و OR. وكل عنصر منطقييمكن تنفيذها باستخدام ترانزستورات متعددة. أو حتى تتابع . مثال على تنفيذ مُعلِن كامل على ترانزستورات CMOS . المصدرلذلك وصلنا إلى الترانزستور! على الرغم من ، بالطبع ، لا تعمل وحدات ALU فقط على الترانزستورات ، ولكن أيضًا وحدات المعالج الأخرى ، ولكن يتم استخدام معظم الترانزستورات في ذاكرة التخزين المؤقت كخلاياها.في الواقع ، يمكن بناء دارة الأديم في معالجنا بشكل مختلف وتكون أكثر تعقيدًا. على سبيل المثال ، كانت Intel 8008 قبل 45 عامًا قادرة على حساب جميع بتات الحمل مقدمًا من أجل إجراء الإضافة بالتوازي (ما يسمى بـ adder مع حمل متوازي). من يهتم ، اقرأ منشور المدونة المثير للاهتمام حول الهندسة العكسية ALU Intel 8008 في المدونةكين شريف. على سبيل المثال يتم استخدام العديد من التحسينات: على سبيل المثال ، الضرب مفيد أيضًا لعدم القيام به "وجها لوجه".
مثال على تنفيذ مُعلِن كامل على ترانزستورات CMOS . المصدرلذلك وصلنا إلى الترانزستور! على الرغم من ، بالطبع ، لا تعمل وحدات ALU فقط على الترانزستورات ، ولكن أيضًا وحدات المعالج الأخرى ، ولكن يتم استخدام معظم الترانزستورات في ذاكرة التخزين المؤقت كخلاياها.في الواقع ، يمكن بناء دارة الأديم في معالجنا بشكل مختلف وتكون أكثر تعقيدًا. على سبيل المثال ، كانت Intel 8008 قبل 45 عامًا قادرة على حساب جميع بتات الحمل مقدمًا من أجل إجراء الإضافة بالتوازي (ما يسمى بـ adder مع حمل متوازي). من يهتم ، اقرأ منشور المدونة المثير للاهتمام حول الهندسة العكسية ALU Intel 8008 في المدونةكين شريف. على سبيل المثال يتم استخدام العديد من التحسينات: على سبيل المثال ، الضرب مفيد أيضًا لعدم القيام به "وجها لوجه".الاستنتاجات: ماذا تعلمنا؟
- الأمر معقد
- يظهر بوضوح: لحل مشكلة التعقيد المفرط ، يستخدم المهندسون تقسيم النظم المعقدة إلى مستويات (طبقات).
- توفر البنى متعددة المستويات إمكانية النقل: على سبيل المثال ، يمكن تشغيل Firefox على أنظمة تشغيل مختلفة وعلى أجهزة مختلفة.
- التفاعل بين المستويات يرجع إلى انفتاح المواصفات للواجهات والخدمات وتنسيقات البيانات ، على سبيل المثال HTML و CSS ، C ++ ، مجموعة من أوامر x86 ، إلخ.
- بطل اليوم يعمل في القاع - الترانزستور .
ملاحظة أنا هاوٍ (مطور ويب) ، وأعرف بنية C ++ و ASM و BT قليلاً - من دورة المعهد ، يمكنني أن أفسد شيئًا. لا تتردد في إرسال التعليقات.