مقدمة

تمت كتابة هذا المنشور تحت انطباع هذا المنشور الممتاز من هبر ، حيث يشرح المؤلف بصريًا ، باستخدام النماذج ثنائية الأبعاد التي يرسمها برنامجه ، كيفية عمل النظرية النسبية الخاصة.

أنا أعمل في مجال تكنولوجيا المعلومات ، وبالتعليم - فيزيائي نظري. لفترة طويلة ، كنت مغرمًا بتعميم العلوم ، والفيزياء النظرية على وجه الخصوص. سأحاول ، على غرار المنشور المذكور أعلاه حول النظرية النسبية الخاصة ، أن أشرح بمثال معدة خصيصًا لكيفية عمل ميكانيكا الكم.

النموذج الذي أفكر فيه ليس بأي حال من الأحوال جديدا. قبل أكثر من ستة أشهر ، نشر كريس كانتويل على YouTube إعلانًا عن لعبة جديدة: الشطرنج الكمي (قد يعرف الكثير عن هذا من هذا الفيديو الفيروسي ).

في الآونة الأخيرة ، تم إصدار اللعبة على Steam ، وتكلف 249 روبل. هناك تطبيق آخر - تطبيق مجاني لنظام iOS (لا أعرف ما إذا كان موجودًا على Google Play). ومع ذلك ، في عملية اللعب مع الأصدقاء ، اكتشفت تجريبيًا أن هذا غير صحيح من وجهة نظر ميكانيكا الكم. يمكن أن يسمى هذا التنفيذ الشطرنج الإحصائي بدلاً من الشطرنج الكمومي.

لذلك قررت أن أكتب التنفيذ مع التعقيدات والتراكبات. في تنفيذي ، حاولت تصحيح أوجه القصور هذه ، في رأيي ، موجودة في إصدار Steam (على سبيل المثال ، يمكن أن تتحرك بيادقي أيضًا بحركات كمية ، مثل جميع القطع الأخرى). كل شيء واضح حول تطبيق iOS: يجب أن يكون أي تنفيذ للشطرنج الكمومي كمًا حقيقيًا ، أي ليس فقط أن تكون احتمالية ، ولكن لدعم آثار ميكانيكا الكم مثل التداخل والتشابك ، إلخ.

نسخة ألفا مستضافة على http://truly-quantum-chess.sloppy.zone . هناك يمكنك اللعب مع نفسك ، "اللعب" للاعبين بدورهما ؛ أو العب مباراة كاملة مع صديق. تتم طريقة اللعب مباشرة في المتصفح ، ولا تحتاج إلى تنزيل أي شيء وتثبيته.

تنويه: أنا لا أدعي أن أكون وصفا كاملا لقوانين فيزياء الكم. لكن في المنشور لن تكون هناك صيغة واحدة: الصور فقط ، فقط المتشددين.

تراكب

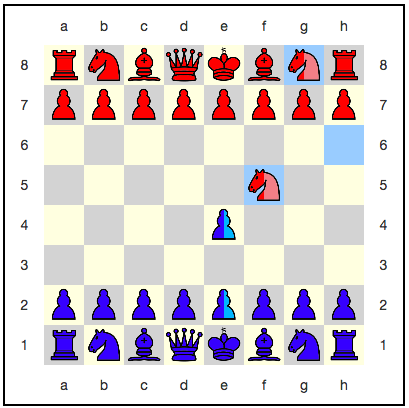
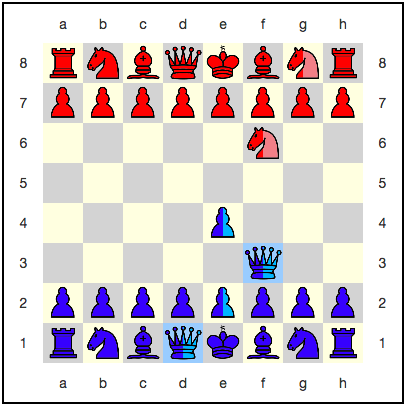
على أية حال ، ما هي هذه الشطرنج الكمومية؟ اختلافهم الرئيسي عن الشطرنج التقليدي هو أن اللعبة تلعب على تراكب ألواح الشطرنج . بعبارات بسيطة - على العديد من المجالس في نفس الوقت.

يبدو شيء مثل هذا:

البيدق الأزرق في تراكب: يحتل الموقعين c2 و c4 في نفس الوقت .
وينطبق الشيء نفسه على الحصان الأحمر: إنه في تراكب المواضع g8 و e3 .

ماذا يعني هذا حقا؟

القارئ ، الذي ينتظر توضيحا حول معنى التراكب ، يجب أن أخيب الآمال: ببساطة لا يوجد تفسير.

التراكبات هي ببساطة تراكبات. هم حقا موجودون في الطبيعة. لا نلاحظها تقريبًا في الحياة اليومية بسبب عدم الترابط - التفاعل مع بيئة فوضوية ، ونتيجة لذلك تنهار التراكبات بسرعة.

ومع ذلك ، لا شيء يمنعنا بشكل أساسي من توفير الظروف التي ستبقى في ظلها التراكب لفترة طويلة. هذه هي بالضبط المهمة التي تواجه ، على سبيل المثال ، المهندسين الذين يعملون على جهاز كمبيوتر الكم.

الاحتمالات

هناك تفسير آخر للتراكب. يمكننا القول أن البيدق الأزرق ليس على مربعين c2 و c4 في نفس الوقت ، ولكن في أحد هذه المربعات. نحن فقط لا نعرف أيهما. علاوة على ذلك ، فإن احتمال التواجد على كل خلية هو 50 ٪ (كما هو موضح بشريط أفقي يقسم كل نصف البيدق إلى النصف).

اتضح ذلك في الواقع

• التفسير الأول (بيدق على e2 و e4 في نفس الوقت) يكون أكثر دقة عندما لا يتفاعل النظام مع جهاز القياس. حول ما يجب اعتباره جهاز قياس على رقعة الشطرنج ، سنذهب أبعد من ذلك في قسم الانهيار.
• التفسير الثاني (بيدق على e2 أو e4 ، نحن لا نعرف أين) أكثر دقة في وقت التفاعل مع البيئة ، على سبيل المثال ، مع جهاز قياس.

على الرغم من عدم وجود تفاعل ، فإن كلا الخيارين (بيدق على e2 و e4 ) موجودان بمفردهما . يتم لعب اللعبة على تراكب من الخيارات. هذه عملية معقدة تمزج بين كلا الخيارين بشكل طبيعي ، وتجبرهم على التأثير في بعضهم البعض. لذلك ، لا يمكن القول أن هناك خيار واحد فقط.

عندما يتم تشغيل التفاعل ، يكون التفسير الاحتمالي صحيحًا. احتمال العثور على البيدق على e2 في هذه الحالة هو 50 ٪. محرك الشطرنج الكمومي ، بالضرورة ، يحل مثل هذه الحالات عن طريق اختيار خيار باستخدام مولد رقم عشوائي.

كيف أقوم بإنشاء تراكب؟

يضاف تغيير واحد مهم لقواعد الشطرنج المعتادة: لكل خطوة يمكن للاعب أن يقوم بها إما بحركة شطرنج عادية أو ما يسمى حركة كمومية.

• الحركة العادية هي ببساطة حركة بقطعة شطرنج ، وفقًا لقواعد الشطرنج العادي. إذا كانت اللعبة يتم لعبها حاليًا في التراكب ، فإن الحركة تتم على جميع لوحات التراكب ، حيث يتم السماح بها وفقًا لقواعد الشطرنج . هذا ، بالمناسبة ، أبعد ما يكون عن التافهة كما يبدو. على سبيل المثال ، إذا كان البيدق في التراكب على مسار الرخ ، فإن هذه الخطوة ممكنة فقط إذا لم يكن هناك رهن (لأنه ، وفقًا للقواعد ، لا يمكن أن ينقض الرخ فوق القطع). لذلك ، بعد مثل هذه الخطوة العادية ، سيكون الرخ نفسه في تراكب: على اللوحة التي لا يوجد بها بيدق ، قامت بحركة ؛ وعلى السبورة التي على البيدق في الطريق ، الحركة ممنوعة ، لذا يبقى الرخ في مكانه.

  
  

• الحركة الكمومية هي حركة يمكنك من خلالها إدخال رقعة الشطرنج في تراكب. تتكون الحركة الكمية من حركتين عاديتين متتاليتين بنفس القطعة. يجب أن تكون كلتا الحركتين صحيحة من وجهة نظر الشطرنج العادي (بشكل صحيح أكثر ، يتم تطبيق خطوة على اللوحة من التراكب إذا كانت كلتا الحركتين صحيحة من وجهة نظر الشطرنج العادي على هذه اللوحة). نوع من "الدفع" للفرصة للذهاب مرتين متتاليين هو أنه بعد الحركة الكمية ، يتحول الرقم إلى تراكب : يقوم في وقت واحد بحركتين ويبقى في مكانه. بعد ذلك ، عندما يحدث التفاعل (انظر أدناه في "الانهيار") ، باستخدام مولد رقم عشوائي ، سيتم تحديد أي من جزأ التراكب موجود وأيهما غير موجود. ولكن بينما يوجد كلا الجزأين في وقت واحد.

  
  

للقيام بحركة عادية ، تحتاج إلى النقر فوق الشكل (المميز باللون الأخضر) ، ثم على الخلية التي تريد الذهاب إليها. لإجراء حركة كمومية ، تحتاج إلى النقر المزدوج على الشكل (مظلل باللون البنفسجي) ، ثم النقر مرة واحدة على الخلية المتوسطة (مظللة باللون الأخضر) ، ثم على الشكل النهائي.

أيضًا ، يُسمح للقواعد بإجراء حركات كمية واحدة ، أي يتحرك الكم ، حيث لا يقوم الشكل بحركتين متتاليتين ، بل حركة واحدة.

قيد مهم: وفقًا للقواعد ، لا يمكنك أكل شخصية العدو في حركة كمية. مثل هذه الفرصة تجعل اللعبة غير متوقعة للغاية. لا يمكن القيام بحركة كمية إلا على خلية فارغة.

ميت وحي

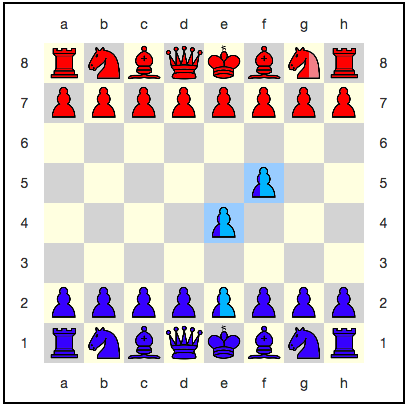
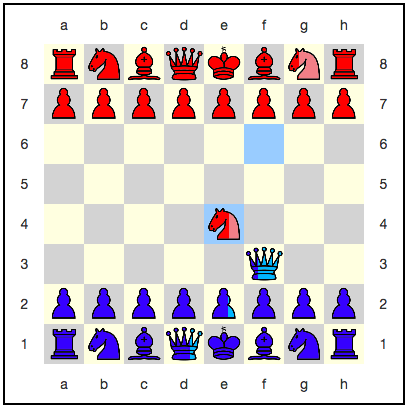
حالة خاصة من التراكب ذات الاهتمام الخاص هي التراكب الذي يكون فيه الشكل حيًا وماتًا. خذ على سبيل المثال رقعة الشطرنج الكمومي من المثال أعلاه. بعد تحريك البيدق الأزرق f2: e3 ، يخسر الحمر نصف فارسهم ...

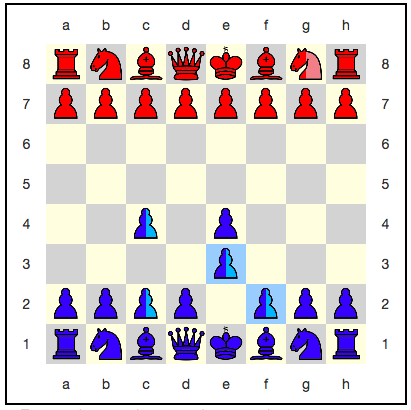
أولاً ، كان البيدق الأزرق نفسه في تراكب. وذلك لأن البيادق تمشي وتناول الطعام بطرق مختلفة. على اللوح الذي كان الفارس الأحمر على e3 ، يأكله البيدق بنجاح ويتحول إلى e3 . على اللوح الذي لم يكن الفارس موجودًا فيه ، لم يتمكن البيدق من القيام بهذه الخطوة ، لأنه لم يكن لديها ما تأكله. لذلك ، بقيت في ص.

تبين أن الحصان الأحمر على قيد الحياة وميت. في وقت ما في المستقبل ، عندما يكون هناك تفاعل مع جهاز القياس (لمزيد من المعلومات حول هذا ، راجع قسم "الانهيار" أدناه) ، سيتم حل هذا الموقف باستخدام مولد رقم عشوائي. إما أنه تبين أن الحمر لديهم حصان ، أو اتضح أنه ليس لديه حصان. احتمال النتائج 50٪.

من الجدير بالذكر أنه حتى يتم حل الوضع ويكون الحصان في تراكب ، يمكن للحمر مواصلة اللعب مع نصف حصانهم. صحيح ، مع احتمال 50 ٪ اتضح أن كل حركة بحلول هذا النصف من الفارس هي ببساطة خسارة بدوره.

كش ملك

من الصعب للغاية تنفيذ الشيكات والحصائر ، لأنه ليس من الواضح ما يجب فعله في موقف يكون فيه الملك في تراكب الشيك وليس الشيك ؛ رفيقة وليس رفيقة. لذلك ، تم تبسيط قواعد الشطرنج العادي: لا يوجد لعبة الداما أو زملائه ؛ من أجل الفوز بالشطرنج الكمومي ، عليك أن تأكل ملك العدو.

يشار إلى أن الملك ، مثل أي شخصية أخرى ، يمكن أن يكون في تراكب. إذا أكلت نصف الملك ، فإن الفوز مضمون باحتمال 50٪. ومع ذلك ، تستمر اللعبة في هذه الحالة! إذا أكل ، على سبيل المثال ، ملكك بعد ذلك ، فهذا لا يعني أنك خسرت. بعد كل شيء ، تم أكل ملكك فقط على ألواح التراكب التي لم تفز بها بعد! على سبيل المثال سيتم إنشاء رقم عشوائي وستفقد / تربح بنسبة 50٪.

هذا أحد الأمثلة على "التفاعل مع جهاز القياس" الذي يدمر التراكبات على رقعة الشطرنج الكمومي.

زر Capitulate بعيد أيضًا عن كونه بسيطًا كما يبدو. الاستسلام يحدث فقط على تلك الألواح من التراكب التي لا تزال اللعبة جارية. على سبيل المثال إذا كنت في تراكب فزت فيه بالفعل باحتمال 75٪ (أي أن العدو لديه 25٪ من الملك) وقمت بالنقر فوق استسلام ، فستخسر باحتمالية 25٪. واحتمال 3/4 تفوز باستسلام! المزيد عن هذا في القسم التالي:

الخلود الكمومي والحماية منه

يمكن أن يكون زر Capitulate مفيدًا للحماية من إستراتيجية اللعبة بناءً على ما يسمى. خلود الكم . دعونا نتناول هذا بمزيد من التفصيل.

فكر في وضع الشطرنج هذا:

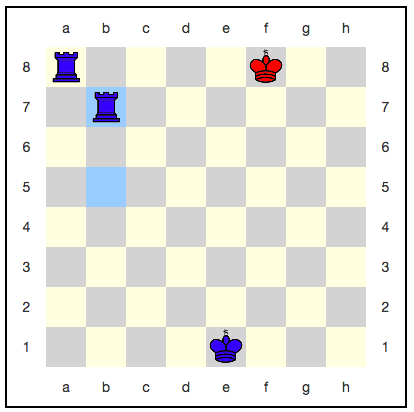
في الشطرنج العادي ، هو زميل كلاسيكي مع رختين. ولكن في الشطرنج الكمومي ، لا توجد حصائر ، بل تحتاج إلى أكل الملك.

يبدو أن الملك هنا ليس لديه مكان للتراجع: الخطوة التالية ستأكله بالتأكيد. ومع ذلك ، هناك استراتيجية تستخدم الخلود الكمي: يمكن للأحمر أن يسحقوا ملكهم مع كل حركة ، ولن يتم تناوله بالكامل. على سبيل المثال ، إليك سلسلة من التحركات:

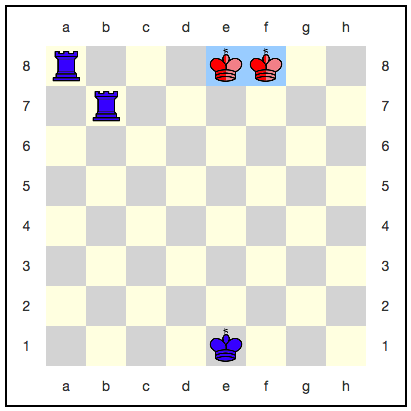
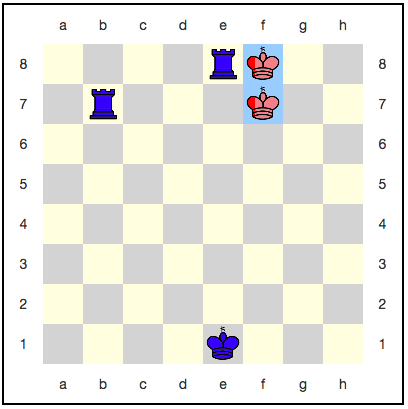
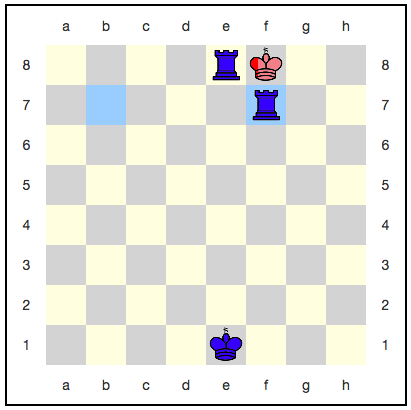
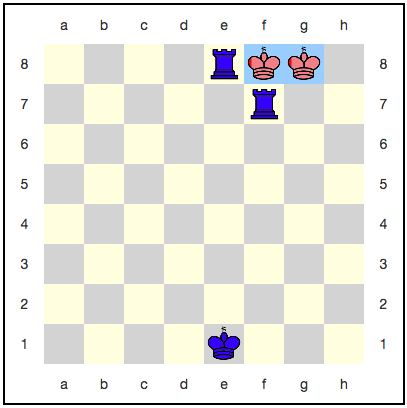
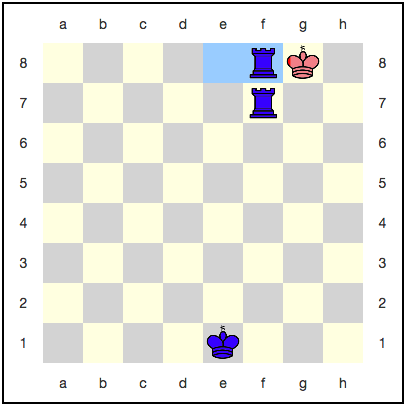
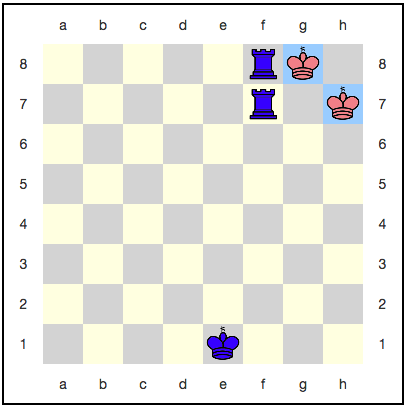
مع كل خطوة ، يزداد احتمال الفوز باللون الأزرق ، لكنه لن يصل إلى واحد. اتضح أن اللعبة ستستمر إلى الأبد ، والأزرق لن يحصل على نصر مستحق؟

في مثل هذه الحالة ، الغريب ، الاستسلام مفيد. إذا كان احتمال فوز اللون الأزرق متساويًا ، على سبيل المثال ، 65535/65536 ، فيمكنك النقر بأمان على الاستسلام. كما هو موضح أعلاه ، سيحدث الاستسلام فقط على تلك الألواح من التراكب التي لا تزال اللعبة جارية. على سبيل المثال الفوز الأزرق باحتمالية 65535/65536 ، يستسلم فقط!

حسنًا ، إذا كان يعمل 1/65536 ... ربما يكون هذا مزعجًا بشكل رهيب :)

الانهيار: نفس "التفاعل مع جهاز القياس"

في الشطرنج الكمومي ، يُسمح بتراكب قطع تعسفي. علاوة على ذلك ، فإن إنشاء التراكبات ليس أمرًا ممتعًا فقط: كونك مبتدئًا في الشطرنج العادي واللعب ضد أحد كبار المدراء ، يمكنك بسهولة تمييع ميزته أمامك من خلال إدخال اللوحة في تراكبات معقدة!

ومع ذلك ، هناك تراكبات تعتبر مجنونة للغاية. مثل هذه التراكبات لا يمكن أن توجد. بمجرد ظهورها ، يبدأ محرك الشطرنج الكمي آلية تدمير مثل هذه التراكبات ، أو "التفاعل مع جهاز القياس".

المعيار بسيط: لا يمكن أن يكون هناك تراكب تشغل فيه الخلية نفسها شكلين أو أكثر في نفس الوقت. توافق ، سيكون الأمر مربكًا وصعبًا للغاية إذا كان لديك حصان وغزو العدو في نفس المربع في نفس الوقت؟

تراكب الأشكال مقابل تراكب الألواح

من الجدير بالذكر هو عملية كسر التراكبات. نحن في أي تراكب (من أجلهم تم إنشاء اللعبة) ، لذلك ، مع الانهيار نريد حفظ أكبر عدد ممكن من التراكبات. على سبيل المثال ، خذ بعين الاعتبار هذا الموقف:

ماذا يحدث عندما يأخذ البيدق الأزرق الفارس الأحمر e4: f5 ؟

أحد الأخطاء المنطقية الشائعة التي يمكن ارتكابها في ميكانيكا الكم هو الفهم العام غير الكافي للتراكبات. على سبيل المثال ، إذا جادلت من وجهة نظر الشخصيات الفردية - لنفترض أن هذا بيدق ، إنه في حالة تراكب - فمن السهل جدًا أن تقود نفسك إلى طريق مسدود.

لمنع حدوث ذلك ، أضمن طريقة هي أن تتذكر أن النظام بأكمله دائمًا في تراكب ، أي في حالتنا ، رقعة الشطرنج. ليس من المستغرب أن يعمل محرك الشطرنج الكمومي على هذا المبدأ. ضع في اعتبارك الحالة أعلاه في عرض المحرك:

يمكن ملاحظة أن المحرك يمثل تراكبًا بالضبط في الشكل المذكور أعلاه: كمجموعة من الألواح. في هذه الحالة ، يمكن استخدام الألواح الأربعة الموضحة أعلاه ، حيث يمكن للفارس الأحمر والبيدق الأزرق أن يتحركوا أو لا. توجد رقعة الشطرنج الكمومية في تراكب أربعة ألواح عادية.

هذا التمثيل أكثر دقة ، ويزود المستخدم بمعلومات كاملة حول الحالة الكمية للوحة الشطرنج. في الاختلاف عن التمثيل في الواجهة التي تظهر فقط احتمالات جميع الأشكال. كما هو مخطط ، يجب على اللاعب نفسه الاحتفاظ برأسه بحالة كمية بناءً على التحركات السابقة. إن القدرة على التفكير من حيث ميكانيكا الكم بهذه الطريقة هي ورقة رابحة قوية في يد اللاعب في لعبة الشطرنج الكمومي.

الحد الأدنى من الانهيار

على تراكب الألواح ، من الواضح أنه بعد الخطوة e4: f5 :

1. على اللوح الأول: لا يمكن أن يذهب البيدق قطريًا ، لأنه ليس لديها ما تأكله. لن يتغير شيء ، الخلية f5 فارغة.
2. على اللوح الثاني: سوف يتمكن البيدق من أكل الفارس. يوجد بيدق في الخلية f5 .
3. على اللوحة الثالثة: ببساطة لا توجد بيادق على e4 . فشل النقل ، الخلية f5 فارغة.
4. على اللوحة الرابعة: لا توجد بيادق مرة أخرى على e4 . فشلت الخطوة ، ظل الحصان على f5 .

بعد تطبيق هذه الخطوة ، ينشأ صراع بين الفارس والبيدق فوق الخلية f5 . على اللوحة الثانية يوجد الآن بيدق ، وفي الرابع - فارس.

كما ناقشنا بالفعل ، نريد حل هذا الصراع ، مع تدمير أقل عدد ممكن من التراكبات. لذلك:

• لا يتعارض المجالس الأول والثالث مع أي شخص. لذلك ، لا ينبغي أن يؤثر الانهيار عليهم. سيبقون ، وستستمر اللعبة عليهم.
• تتعارض المجالس الثانية والرابعة مع بعضها البعض. لذلك ، فيما بينها ، باستخدام مولد الأرقام العشوائية ، يتم تحديد خيار البقاء على قيد الحياة ، مع احتمال 50/50.

الخيار الأول: نجا الحصان

يتم التخلص من اللوحة الثانية ، وتستمر اللعبة على تراكب الألواح مع الأرقام 1 ، 3 ، 4:

لاحظ أنه تم إعادة توزيع الاحتمال الخلفي للبيدق! الآن ، مع احتمال 2/3 ، يكون البيدق على e2 (الألواح 3 و 4) ، ومع احتمال 1/3 يكون على e4 (اللوحة 1).

هذا صحيح! في البداية ، كان البيدق على e2 باحتمال 50٪ ، لكن هذا الاحتمال تغير بعد توليد الرقم العشوائي . كان الاحتمال الخلفي 66.7٪.

وينطبق الشيء نفسه على الحصان (يمكن للقارئ عد الألواح والتأكد من أن احتمال العثور على الحصان على f5 قد تغير من 50٪ إلى 33.3٪).

هكذا تبدو النتيجة في الواجهة:

الخيار الثاني: أكل الحصان

يتم التخلص من اللوحة الرابعة ، وتستمر اللعبة على تراكب الألواح بالأرقام 1 ، 2 ، 3:

في هذه الحالة ، الحصان الآن في تراكب الأحياء والأموات ، مثل قطة شرودنغر. وبيدق محتمل بنسبة 33.3٪ ينتشر على المراكز e2 ، e4 ، f5 . هكذا تبدو النتيجة في الواجهة:

تشابك الكم

واحدة من أكثر الظواهر شهرة وإثارة في العالم الكمي هي التشابك الكمي. نظر آينشتاين لأول مرة في تجربة فكرية تسمى مفارقة EPR :

ضع في اعتبارك زوج الجسيمات المضادة للجسيمات التي تشكلت خلال تحلل جسيم أثقل (أي يستريح) ، على سبيل المثال ، ميزون. جادل أينشتاين أنه وفقًا لقانون الحفاظ على الزخم ، فإن عزم الجسيم والجسيم المضاد مرتبطان بقانون الحفاظ على الزخم ؛ مما يعني أنه من خلال قياس إحداثيات الجسيم وزخم الجسيم المضاد ، يمكن للمرء حساب زخم الجسيم باستخدام هذا القانون ، وبالتالي عن طريق قياس عزم الجسيم والجسيم المضاد تنتهك مبدأ الارتياب لهايزنبرج. هل هذا يعني أن "الوصف الميكانيكي الكمومي للواقع ليس كاملاً" ©؟

اقترح بوهر حلاً لهذه المفارقة: بعد قياس زخم الجسيم ، فإن زخم الجسيم المضاد يغير قيمته على الفور ، مما يعني أن إحداثياته ​​غير محددة. وبالمثل ، بعد قياس إحداثيات الجسيم المضاد ، تغير إحداثيات الجسيم قيمته على الفور ، مما يعني أن الزخم غير مؤكد.

ما هي طبيعة هذا "الكابوس البعيد المدى"؟

من المعروف الآن بشكل موثوق أن تفسير بور صحيح. اتضح أنه أكثر منطقية ومفهومة إذا ترجمناها إلى اللغة الصحيحة: يجب أن نقدم عبارات حول تراكب نظام الجسيمات + الجسيمات ، وليس حول تراكب مكوناته الفردية.

تأمل هذا الموقف في مثال توضيحي أكثر بكثير: على رقعة شطرنج كمومية.

تشابك في الشطرنج الكمومي

تتيح لك رقعة الشطرنج الكمومي أن تشعر بمفهوم تشابك الشطرنج. من أجل ترجمة اللوحة إلى حالة تشابك الشطرنج ، تحتاج إلى ... المرور بقطعة من خلال قطعة أخرى. فكر في مثال:

الأزرق يذهب الملكة (الملكة) d1: f3 . هذه حركة عادية غير كمية! ولكن هذا غير ممكن على جميع لوحات التراكب. دعونا نرى كيف يبدو الوضع في عرض محرك الشطرنج الكمومي:

يمكن إجراء تحرك على اللوحين 1 و 3 ، أي على اثنين من أربعة مجالس. لذلك ، في هذه الحالة ، ستدخل الحركة غير الكمومية المعتادة الملكة الزرقاء في تراكب:

ومع ذلك ، هناك شيء لا يمكن ملاحظته على الفور. دعونا نلقي نظرة على عرض المحرك:

بيان: الملكة منتشرة في موقعين d1 و f3 باحتمالات 50٪. e2 e4 50%, : e2 , – d1 ; e4 – f3 .

, -. !

, f6:e4 . e4 , . :

, (66.7% e2 33.3% ) .

:

" " -. ; ( – ) , . , . , ( ), .

, – , ; , .. – , .

, . , . , , . , .. .

, , e4 f3 25%, , 50%, .

الخلاصة

. , .

:

1. – ,
2. -

, ; , . , – .

!