🛷 💆🏻 💻 التآمر مع محورين مستقلين في ماتلاب 🤜🏿 👨‍❤️‍💋‍👨 🦒

ستكون هذه المقالة مفيدة لأولئك الذين يرسمون رسومات في بيئة Matlab.

عند إعداد الرسوم البيانية لنشر المقالات في المجلات العلمية وأنواع مختلفة من التقارير ، غالبًا ما صادفت الحاجة إلى بناء العديد من المنحنيات ، كل منها مرتبط بمحورها - حتى لا تفرط في تحميل المقالة مع الرسوم البيانية ولا تتجاوز حدودها. ولكن لهذا ، في Matlab قبل الإصدار R2014a ، لم يكن هناك سوى فريق plotyy (X1 ، Y1 ، X2 ، Y2) ، الذي يحتوي على عدد من الميزات غير السارة ، والتي كان من الضروري استخدام برامج أخرى والقيام بكل شيء يدويًا ، مما يؤدي أولاً إلى تعقيد هذه العملية مع من وجهة نظر نمط واحد ، ثانيًا ، يتطلب الكثير من الوقت ، وثالثًا ، لا يسمح بالتغييرات السريعة.

ميزات ووصف غير سارة

إلى هذه الميزات غير السارة ، أود أن أعزو:

1. عدم وجود تمثيلية في الانتظار (لا يعمل التمسك "الأصلي" بشكل صحيح مع plotyy). لإضافة أكثر من منحنيين ، تحتاج إلى استخدام هذا البناء:

[hAx,hLine1,hLine2] = plotyy([x1',x2'],[y1' y2'],[x3',x4'],[y3',y4']); % 4

يتبع هذا التصميم ميزة غير سارة رقم 2:

2. يجب أن تتطابق أبعاد المصفوفات الموجودة بين قوسين مربعين ، لأن يتم تشكيل مصفوفات العناصر منها. عمليًا ، نادرًا ما يحدث هذا.

3. يعاني التصميم بجدية من حقيقة أنه لا يمكنك تغيير ألوان وأنواع جميع الخطوط في صف برمجيًا ، يمكنك تنسيق مجموعة فقط من الخطوط المتعلقة بمحور معين (hLine1 و hLine2) - على أي حال ، لم أستطع. في الوقت نفسه ، لا أتحدث عن تغيير المعلمات يدويًا ، أي التحرير في نافذة "الشكل" - فقط مباشرة مع الرمز الموجود في ملف .m.

تلخيص ما سبق: plotyy () ليس مناسبًا جدًا لعرض مجموعات متعددة من الرسوم البيانية لمحاور مختلفة. ما لم تبعيات بسيطة مثل هذه:

 x = linspace(0,10); y1 = 200*exp(-0.05*x).*sin(x); y2 = 0.8*exp(-0.5*x).*cos(10*x); y3 = 0.2*exp(-0.5*x).*cos(10*x); y4 = 150*exp(-0.05*x).*sin(x); X=[x',x']; Y1=[y1' y4']; Y2=[y2',y3']; [hAx,hLine1,hLine2] = plotyy(X,Y1,X,Y2);

إما فريق yyaxes ، الذي ظهر في إصدار Matlab R2014a. هنا لدينا الآن المكان الذي نستدير فيه.

أود أن أخبركم عن مباهج هذا الفريق باستخدام المثال الخاص بي. المهمة هي أنني بحاجة إلى البناء على ملف شخصي واحد لدرجة الحرارة 3 (الحلول التي تم الحصول عليها بواسطة الطريقة العددية المباشرة ، وطريقة العزم والقيم التجريبية) المتعلقة بالمحور الأيمن ، و 3 ملفات تعريف الضغط المتعلقة بالمحور الأيسر. وإضافة السهام والتسميات التوضيحية أيضًا.

أوامر yyaxis اليسرى و yyaxis اليمنى تسمح لك بالتعامل مع هذه المهمة في وقت واحد. ما هو في الواقع الجوهر. ضمن رقم واحد ، يمكننا بناء أي عدد من الرسوم البيانية عن طريق ربطها بأحد المحاور. في إطار كل فريق ، يعمل كل شيء كما هو الحال مع الجداول العادية.

سيبدو هيكل الصورة في هذه الحالة كما يلي:

 figure() {     - , } yyaxis left { ,     - , , ,       } yyaxis right { ,     - , , ,       }

نملأ هذا الهيكل بالضروري الذي نحصل عليه نتيجة لذلك:

كود البرنامج

 %     h = figure('Units', 'normalized', 'OuterPosition', [0 0 1 1]); %  : F='Times New Roman'; FN='FontName'; FS='FontSize'; l=30;%   set(gca, FN, F, FS, l) box on %  hold on %%   yyaxis right hPlot_1 = plot(time*10^6, T); %    hPlot_2 =plot(time_exp_T*10^6, T_exp); %   hPlot_3 =plot(time_pk, T_pk); %   set( hPlot_1, 'LineWidth', 3, 'LineStyle', ':', 'Color', 'k' ); set( hPlot_2, 'LineWidth', 1, 'LineStyle', 'none', 'Color', 'k', 'Marker', 'o' ); set( hPlot_3, 'LineWidth', 3, 'LineStyle', '--', 'Color', 'k' ); %    () ylim([180 270]); %     () yticks([190 200 210 220 230 240 250 260 267]) yticklabels({'190', '200', '210', '220', '230', '240','250' '260', '\it T, K'}) %   set(gca,'xcolor','k'); set(gca,'ycolor','k'); %%   yyaxis left hPlot_10 = plot(time_P*10^6, P_p0); %    hPlot_11 = plot(time_exp_P_p0*10^6, P_p0_exp); %   hPlot_13 = plot(time_pk, Pp0_pk); %   set( hPlot_10, 'LineWidth', 3, 'LineStyle', ':', 'Color', 'k' ); set( hPlot_11, 'LineWidth', 1, 'LineStyle', 'none', 'Color', 'k', 'Marker', 'x' ); set( hPlot_13, 'LineWidth', 3, 'LineStyle', '--', 'Color', 'k' ); %    () ylim([0.1 0.8]); %     () yticks([0.2 0.3 0.4 0.5 0.6 0.7 0.77]) yticklabels({'0.2', '0.3', '0.4', '0.5', '0.6', '0.7', '\it p/p_0 '}) %   set(gca,'xcolor','k'); set(gca,'ycolor','k'); %%   %      xticks([0 20 40 60 80 100 120 140 160 185]) xticklabels({'0' '20' '40' '60' '80' '100' '120' '140' '160', '\it X/U, c'}) %  text(20,0.3,'\leftarrow', FS, 60, FN, F); text(140,0.6,'\rightarrow', FS, 60, FN, F); text(160,0.24,'1', FS, l, FN, F); text(60, 0.25,'2', FS, l, FN, F); text(120, 0.2,'3', FS, l, FN, F); text(140,0.51,'4', FS, l, FN, F); text(80, 0.52,'5', FS, l, FN, F); text(120,0.48,'6', FS, l, FN, F); text(5,0.75,'\it D_2O - N_2', FS, l, FN, F); hold off

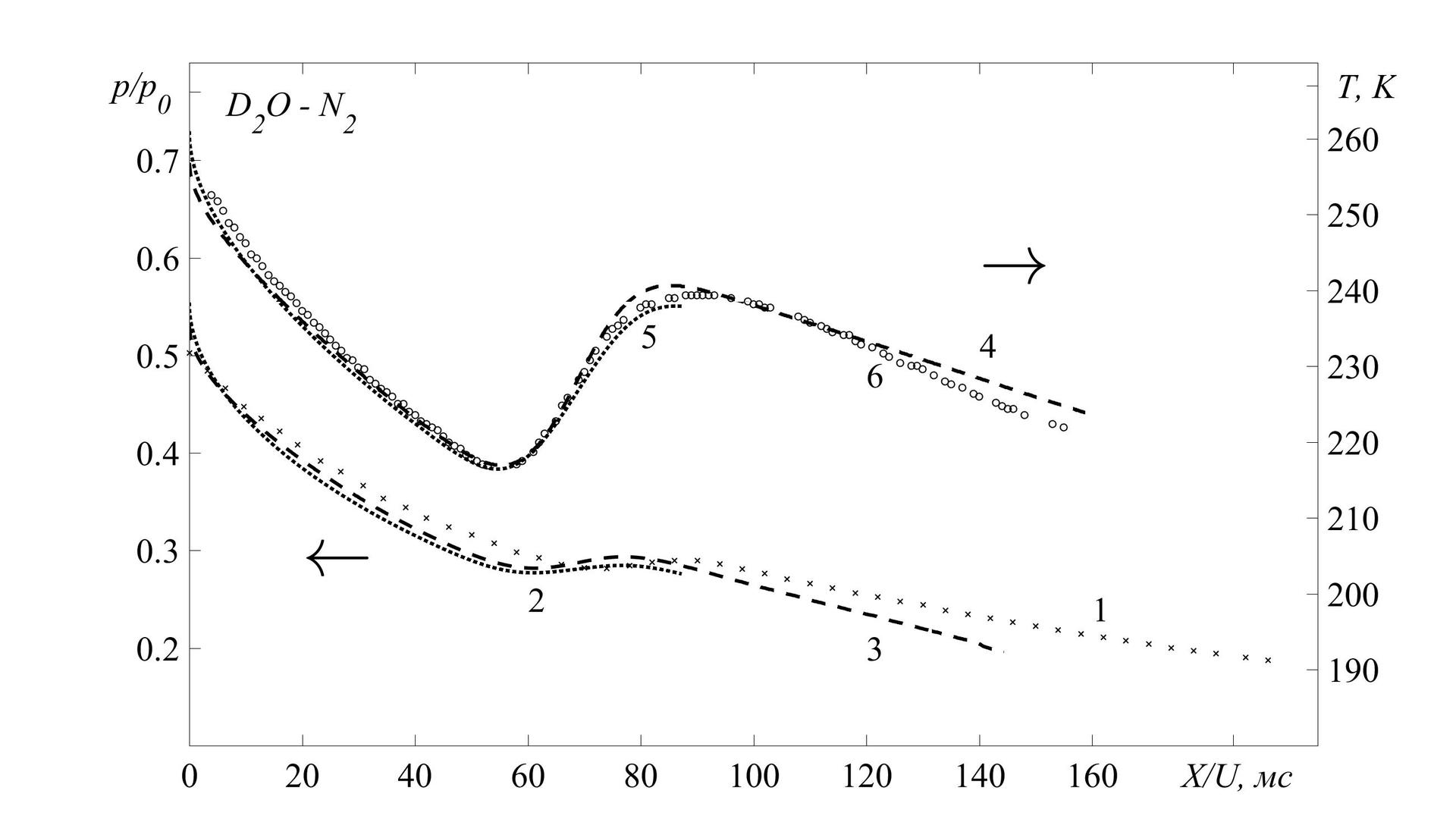
ميزة إضافية أخرى في إعداد الرسوم البيانية للطباعة هي حفظها البسيط والمريح بأي تنسيق يدعمه Matlab. للقيام بذلك ، تحتاج فقط إلى إضافة الأسطر التالية:

 %%   file_name = strcat('T, p_p0 - mm, ch, exp'); %   saveas(h, file_name, 'bmp'); %  .bmp saveas(h, file_name, 'fig'); %  .fig saveas(h, file_name, 'eps'); %  .eps saveas(h, file_name, 'jpeg'); %  .jpeg close(h); %

الملخص

بدءًا من الإصدار R2014a ، أصبح Matlab برنامجًا مناسبًا لإعداد جداول لنشر المقالات في المجلات العلمية المختلفة. ميزة مهمة أخرى هي المرونة الجيدة جدًا لهذه الأداة ، والتي تسمح لك بمعالجة النتائج وتقديمها في شكل سهل الهضم وجميل ، بما في ذلك ما يسمى ب. معالجة "دفعة".

الأمر يستحق نظرة خاطفة:

→ مقال مفيد عن الرسوم البيانية في Matlab
→ وصف yyaxis

→ وصف plotyy
→ مخططات التصدير

التآمر مع محورين مستقلين في ماتلاب

More articles: