مقدمة للجزء الأول
نمذجة التوربينات البخارية هي مهمة يومية لمئات الأشخاص في بلدنا. بدلاً من كلمة " نموذج" ، من المعتاد أن تقول خاصية حساب . تُستخدم خصائص استهلاك التوربينات البخارية في حل مشكلات مثل حساب الاستهلاك المحدد للوقود المكافئ للكهرباء والحرارة التي تنتجها محطات الطاقة الحرارية ؛ تحسين CHP ؛ تخطيط وصيانة طرق محطات الطاقة الحرارية.
لقد طورت خاصية تدفق جديدة لتوربين بخاري - خاصية تدفق خطية لتوربين بخاري. إن خاصية التدفق المطورة ملائمة وفعالة في حل هذه المشاكل. ومع ذلك ، يتم وصفه حاليًا في ورقتين علميتين فقط:
- تحسين تشغيل محطات الطاقة الحرارية في ظروف سوق الجملة للطاقة الكهربائية وسعة روسيا
- الطرق الحسابية لتحديد الاستهلاك المحدد للوقود المكافئ لمحطات الطاقة الحرارية للطاقة الكهربائية والحرارية الموردة في وضع التوليد المشترك .
والآن في مدونتي أود أن:
1. البيانات المصدر
يمكن أن تكون البيانات الأولية لبناء خاصية التدفق الخطي
- قيم الطاقة الفعلية Q 0 ، N ، Q p ، Q t المقاسة أثناء تشغيل التوربين البخاري ،
- nomograms q t الإجمالي من الوثائق المعيارية والتقنية.
بالطبع ، تعد القيم اللحظية الفعلية لـ Q
0 و N و Q
p و Q
t بيانات مصدر مثالية. يستغرق جمع هذه البيانات وقتًا طويلاً.
في الحالات التي لا تكون فيها القيم الفعلية Q 0 و N و Q p و Q t متاحة ، يمكنك معالجة الرموز التخطيطية q t الإجمالية. تم الحصول عليها بدورها على أساس القياسات. اقرأ المزيد عن اختبارات التوربينات في VM Gornstein وطرق أخرى لتحسين أوضاع أنظمة الطاقة .
2. خوارزمية تكوين خصائص التدفق الخطي
تتكون خوارزمية البناء من ثلاث خطوات.
- ترجمة المخططات أو نتائج القياس في عرض جدولي.
- الخطي لخاصية التدفق للتوربين البخاري.
- تحديد حدود نطاق التحكم في التوربين البخاري.
عند العمل مع nomograms q t إجمالي ، تكون الخطوة الأولى سريعة. هذا العمل يسمى الرقمنة . استغرقت رقميّة 9 رموز للمثال الحالي حوالي 40 دقيقة.
تتطلب الخطوتان الثانية والثالثة استخدام الحزم الرياضية. أنا أحب واستخدام MATLAB لسنوات عديدة. المثال الخاص بي لبناء خاصية التدفق الخطي مصنوع فيه. يمكن تنزيل مثال من الرابط وتشغيله واستخلاص طريقة إنشاء خاصية التدفق الخطي بشكل مستقل.
تم إنشاء خاصية التدفق للتوربين المعني للقيم الثابتة التالية لمعلمات الوضع:
- عملية أحادية المرحلة
- ضغط البخار متوسط الضغط = 13 كجم / سم 2 ،
- ضغط بخار منخفض الضغط = 1 كجم / سم 2.
محتويات أرشيف Chuchueva-PT-80-linear-مميزة-منحنى . rar .
1) Nomograms من إجمالي استهلاك qt الإجمالي لتوليد الكهرباء (يتم ترقيم النقاط الحمراء المميزة - نقلها إلى الجدول):
- PT80_qt_Qm_eq_0_digit.png ،
- PT80_qt_Qm_eq_100_digit.png،
- PT80_qt_Qm_eq_120_digit.png،
- PT80_qt_Qm_eq_140_digit.png،
- PT80_qt_Qm_eq_150_digit.png،
- PT80_qt_Qm_eq_20_digit.png،
- PT80_qt_Qm_eq_40_digit.png،
- PT80_qt_Qm_eq_60_digit.png،
- PT80_qt_Qm_eq_80_digit.png.
2) نتيجة الرقمنة (يتوافق كل ملف csv مع ملف png):
- PT-80_Qm_eq_0.csv ،
- PT-80_Qm_eq_100.csv ،
- PT-80_Qm_eq_120.csv ،
- PT-80_Qm_eq_140.csv ،
- PT-80_Qm_eq_150.csv ،
- PT-80_Qm_eq_20.csv ،
- PT-80_Qm_eq_40.csv ،
- PT-80_Qm_eq_60.csv ،
- PT-80_Qm_eq_80.csv.
3) برنامج MATLAB مع الحسابات والرسوم البيانية:
- PT_80_linear_characteristic_curve.m
4) نتيجة رقمنة المخططات ونتيجة بناء خاصية تدفق خطي في شكل جدولي:
- PT_80_linear_characteristic_curve.xlsx.
الخطوة 1. ترجمة الرموز أو نتائج القياس في طريقة عرض جدولية
1. معالجة البيانات المصدر
البيانات الأولية لمثالنا هي إجمالي الرسوم البيانية q t .
لرقمنة العديد من الرموز ، تحتاج إلى أداة خاصة. لقد استخدمت مرارًا وتكرارًا تطبيق ويب لهذه الأغراض. التطبيق بسيط ومريح ، ولكن ليس لديه مرونة كافية لأتمتة العملية. جزء من العمل يجب القيام به يدويا.
في هذه الخطوة ، من المهم رقمنة النقاط القصوى من المخططات التي تحدد حدود نطاق تعديل التوربين البخاري .
كانت المهمة هي تحديد نقاط خاصية التفريغ في كل ملف png باستخدام التطبيق ، وتحميل ملف csv الناتج وجمع جميع البيانات في جدول واحد. يمكن العثور على نتيجة الرقمنة في الملف PT-80-linear-مميزة- curve.xlsx ، الورقة "PT-80" ، الجدول "بيانات الإدخال".
2. إحضار وحدات القياس إلى وحدات الطاقة
بعد ذلك ، في ورقة "PT-80" ، نحسب قيم Q 0 وفقًا للصيغة
$$ display $$ \ start {equation} Q_0 = \ frac {q_T \ cdot N} {1000} + Q_P + Q_T \ qquad (1) \ end {equation} $$ display $$
ونجلب كل القيم الأولية إلى MW. يتم تنفيذ الحسابات باستخدام MS Excel.
الجدول الناتج "بيانات الإدخال (طاقة الوحدة)" هو نتيجة الخطوة الأولى من الخوارزمية.
الخطوة 2. خطية خاصية تدفق التوربينات البخارية
1. اختبار MATLAB
في هذه الخطوة ، تحتاج إلى تثبيت وفتح إصدار MATLAB لا يقل عن 7.3 (هذا هو إصدار قديم ، 8.0 الحالي). في MATLAB ، افتح الملف PT_80_linear_characteristic_curve.m ، وقم بتشغيله وتأكد من أنه يعمل. كل شيء يعمل بشكل صحيح ، إذا ظهرت نتائج الرسالة التالية عند تشغيل البرنامج النصي في سطر الأوامر:
PT_80_linear_characteristic_curve.xlsx 1 : a(N) = 2.317, a(Q) = 0.621, a(Q) = 0.255, a0 = 33.874 = 0.006, (0.57
إذا كان لديك أي أخطاء ، فاعرف بنفسك كيفية إصلاحها.
2. الحسابات
يتم تنفيذ كافة العمليات الحسابية في الملف PT_80_linear_characteristic_curve.m. دعنا نفكر في ذلك في أجزاء.
1) نشير إلى اسم الملف المصدر والورقة ونطاق الخلايا التي تحتوي على الجدول "بيانات المصدر (وحدة السعة)" التي تم الحصول عليها في الخطوة السابقة.
XLSFileName = 'PT_80_linear_characteristic_curve.xlsx'; XLSSheetName = 'PT-80'; XLSRange = 'F3:I334';
2) نقرأ البيانات المصدر في MATLAB.
sourceData = xlsread(XLSFileName, XLSSheetName, XLSRange); N = sourceData(:,1); Qm = sourceData(:,2); Ql = sourceData(:,3); Q0 = sourceData(:,4); fprintf(' %s %1.0f \n', XLSFileName, toc);
نستخدم Qm المتغير لمتوسط معدل تدفق البخار Q p ، المؤشر m من الوسط هو المتوسط ؛ وبالمثل ، نستخدم Ql المتغير لتدفق البخار منخفض الضغط Q n ، يكون المؤشر l من المنخفض منخفضًا.
3) تحديد المعاملات α i .
تذكر الصيغة العامة لخصائص التدفق
$$ display $$ \ start {equation} Q_0 = f (N، Q_، Q_) \ qquad (2) \ end {equation} $$ display $$
وحدد المتغيرات (x_digit) المستقلة والمتعلقة (y_digit).
x_digit = [N Qm Ql ones(size(N,1),1)];
إذا كنت لا تفهم لماذا تحتوي مصفوفة x_digit على متجه واحد (العمود الأخير) ، فقم بقراءة مواد الانحدار الخطي. حول موضوع تحليل الانحدار ، أوصي بكتاب درابر ن. ، سميث هـ. تحليل الانحدار التطبيقي . نيويورك: وايلي ، في الصحافة ، 1981. 693 ص. (متوفر بالروسية).
معادلة خاصية التدفق الخطي للتوربين البخاري
$$ display $$ \ start {equation} Q_0 = \ alpha_N \ cdot N + \ alpha_ \ cdot Q_ + \ alpha_ \ cdot Q_ + \ alpha_0 \ qquad (3) \ end {equation} $$ display $$
هو نموذج انحدار خطي متعدد. سيتم تحديد المعاملات α i باستخدام "الفائدة العظيمة للحضارة" - طريقة المربعات الصغرى. بشكل منفصل ، ألاحظ أن طريقة المربعات الصغرى تم تطويرها بواسطة Gauss في عام 1795.
في MATLAB ، يتم ذلك في سطر واحد.
A = regress(y_digit, x_digit); fprintf(': a(N) = %4.3f, a(Q) = %4.3f, a(Q) = %4.3f, a0 = %4.3f\n',... A);
يحتوي المتغير A على المعاملات المطلوبة (انظر الرسالة الموجودة في سطر أوامر MATLAB).
وبالتالي ، فإن خاصية التدفق الخطي التي تم الحصول عليها من التوربين البخاري PT-80 لها الشكل
$$ display $$ \ تبدأ {المعادلة} Q_0 = 2.317 \ cdot N + 0.621 \ cdot Q_ + 0.255 \ cdot Q_ + 33.874 \ qquad (4) \ end {المعادلة} $$ display $$
4) نحن نقدر خطأ الخطية لخاصية التدفق التي تم الحصول عليها.
y_model = x_digit * A; err = abs(y_model - y_digit) ./ y_digit; fprintf(' = %1.3f, (%4.2f%%)\n\n', mean(err), mean(err)*100);
الخطأ الخطي هو 0.57٪ (انظر الرسالة في سطر أوامر MATLAB).
لتقييم راحة استخدام خاصية التدفق الخطي للتوربين البخاري ، نحل مشكلة حساب معدل تدفق البخار عالي الضغط Q 0 عند قيم الحمل المعروفة N ، Q p ، Q t .
دع N = 82.3 MW ، Q p = 55.5 MW ، Q t = 62.4 MW ، ثم
$$ display $$ \ تبدأ {المعادلة} Q_0 = 2.317 \ cdot 82.3 + 0.621 \ cdot 55.5 + 0.255 \ cdot 62.4 + 33.874 = 274.9 \ qquad (5) \ end {المعادلة} $$ عرض $$
دعني أذكرك أن متوسط خطأ الحساب هو 0.57٪.
دعونا نعود إلى السؤال ، لماذا تعد خاصية التدفق الخطي للتوربين البخاري أكثر ملاءمة بشكل أساسي من مخططات الاستهلاك المحدد q t الإجمالي لتوليد الكهرباء؟ لفهم الاختلاف الأساسي في الممارسة العملية ، حل مشكلتين.
- احسب Q 0 بالدقة المشار إليها باستخدام المخططات وعينيك.
- أتمتة عملية حساب Q 0 باستخدام المخططات.
من الواضح ، في المهمة الأولى ، أن تحديد القيم الإجمالية q بالعين محفوف بالأخطاء الجسيمة.
المهمة الثانية مرهقة لأتمتة. نظرًا لأن قيم q q غير خطية بشكل إجمالي ، فإن مثل هذه الأتمتة يكون عدد النقاط الرقمية أكبر بعشر مرات من المثال الحالي. الرقمنة وحدها ليست كافية ، فمن الضروري أيضًا تنفيذ خوارزمية لتقريب (العثور على القيم بين النقاط) من القيم الإجمالية غير الخطية.
الخطوة 3. تحديد حدود نطاق ضبط التوربين البخاري
1. الحسابات
لحساب نطاق التعديل ، سنستخدم "خير حضاري" آخر - طريقة بدن محدب ، بدن محدب.
في MATLAB ، يتم ذلك على النحو التالي.
indexCH = convhull(N, Qm, Ql, 'simplify', true); index = unique(indexCH); regRange = [N(index) Qm(index) Ql(index)]; regRangeQ0 = [regRange ones(size(regRange,1),1)] * A; fprintf(' = %d\n\n', size(index,1));
تحدد طريقة convhull () نقاط حدود نطاق الضبط المعطاة بقيم المتغيرات N و Qm و Ql. يحتوي الفهرس المتغير CH على رؤوس مثلثات مبنية باستخدام تثليث Delaunay. يحتوي متغير regRange على نقاط حدود نطاق الضبط ؛ regRangeQ0 المتغير - معدلات تدفق بخار عالية الضغط لنقاط حدود نطاق التحكم.
يمكن العثور على نتيجة الحساب في الملف PT_80_linear_characteristic_curve.xlsx ، الورقة "PT-80-النتيجة" ، الجدول "حدود نطاق الضبط".
بنيت خاصية التدفق الخطي. هي صيغة (4) و 37 نقطة تحدد حدود (نطاق) نطاق الضبط في الجدول المقابل.
2. التحقق
عند أتمتة عمليات الحساب ، Q 0 من الضروري التحقق مما إذا كانت نقطة ما بقيم N ، Q p ، Q t تقع داخل نطاق الضبط أو خارجها (الوضع غير ممكن تقنيًا). في MATLAB ، يمكن القيام بذلك على النحو التالي.
نقوم بتعيين قيم N و Q p و Q t التي نريد التحقق منها.
n = 75; qm = 120; ql = 50;
نتحقق.
in1 = inpolygon(n, qm, regRange(:,1),regRange(:,2)); in2 = inpolygon(qm, ql, regRange(:,2),regRange(:,3)); in = in1 && in2; if in fprintf(' N = %3.2f , Q = %3.2f , Q = %3.2f \n', n, qm, ql); else fprintf(' N = %3.2f , Q = %3.2f , Q = %3.2f ( )\n', n, qm, ql); end
يتم التحقق بخطوتين:
- يشير المتغير in1 إلى ما إذا كانت قيم N ، Q p قد سقطت في إسقاط الصدفة على المحور N ، Q p ؛
- وبالمثل ، يوضح المتغير in2 ما إذا كانت قيم Q p و Q t موجودة داخل إسقاط الصدفة على محور Q p و Q t .
إذا كان كلا المتغيرين يساويان 1 (صحيح) ، فإن النقطة المرغوبة تكون داخل القشرة ، والتي تحدد نطاق ضبط التوربين البخاري.
رسم توضيحي لخاصية التدفق الخطي التي تم الحصول عليها من التوربين البخاري
أكثر "مزايا الحضارة سخاء" التي حصلنا عليها من حيث توضيح نتائج الحسابات.
نحتاج أولاً أن نقول أن المساحة التي نقوم فيها بإنشاء الرسوم البيانية ، أي المساحة ذات المحاور x - N ، y - Q t ، z - Q 0 ، w - Q p ، تسمى مساحة النظام (انظر تحسين تشغيل محطات الطاقة الحرارية في الظروف سوق الجملة للكهرباء وقدرة روسيا
) تحدد كل نقطة من هذه المساحة طريقة معينة لتشغيل التوربين البخاري. قد يكون الوضع
- ممكن من الناحية الفنية ، إذا كانت النقطة داخل القشرة التي تحدد نطاق التعديل ،
- من الناحية الفنية غير مجدية إذا كانت النقطة خارج هذه القشرة.
إذا تحدثنا عن وضع التكثيف في تشغيل التوربين البخاري (Q p = 0 ، Q t = 0) ، فإن خاصية التدفق الخطي هي مقطع خط مستقيم . إذا تحدثنا عن توربين من النوع T ، فإن خاصية التدفق الخطي هي مضلع مسطح في مساحة نظام ثلاثية الأبعاد مع المحاور x - N ، y - Q t ، z - Q 0 ، والتي يسهل تصورها. بالنسبة إلى التوربين من نوع PT ، يكون التصور هو الأكثر صعوبة ، لأن خاصية التدفق الخطي لمثل هذه التوربينات هي مضلع مسطح في مساحة رباعية الأبعاد (للحصول على تفسيرات وأمثلة ، انظر تحسين تشغيل محطة الطاقة الحرارية في سوق الكهرباء والطاقة بالجملة في روسيا ، قسم الخطي لخاصية تدفق التوربينات ).
1. توضيح لخصائص التدفق الخطي للتوربين البخاري
دعونا نبني قيم الجدول "بيانات الإدخال (وحدة الطاقة)" في مساحة النظام.
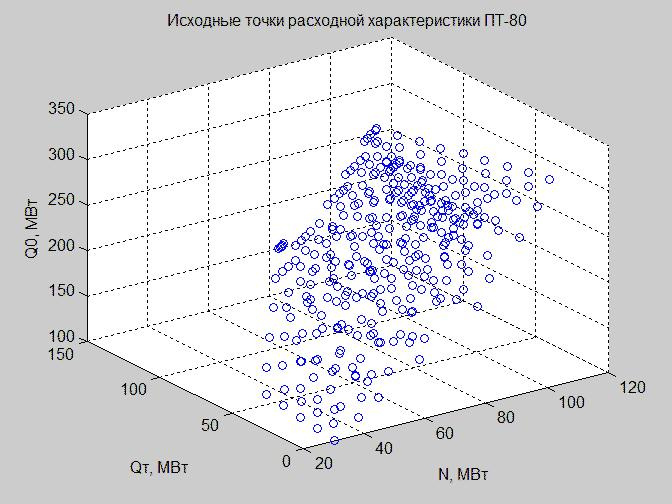
التين. 3. نقاط الانطلاق لخصائص التدفق في فضاء النظام بالمحاور x - N، y - Q t ، z - Q 0
نظرًا لأنه لا يمكننا بناء الاعتماد في الفضاء رباعي الأبعاد ، فإننا لم نصل بعد إلى مثل هذه الحضارة الجيدة ، فنحن نعمل على قيم Q n على النحو التالي: استبعادها (الشكل 3) ، الإصلاح (الشكل 4) (انظر رمز إنشاء الرسوم البيانية في MATLAB).
نقوم بإصلاح قيمة Q p = 40 MW وننشئ نقاط البداية وخاصية التدفق الخطي.
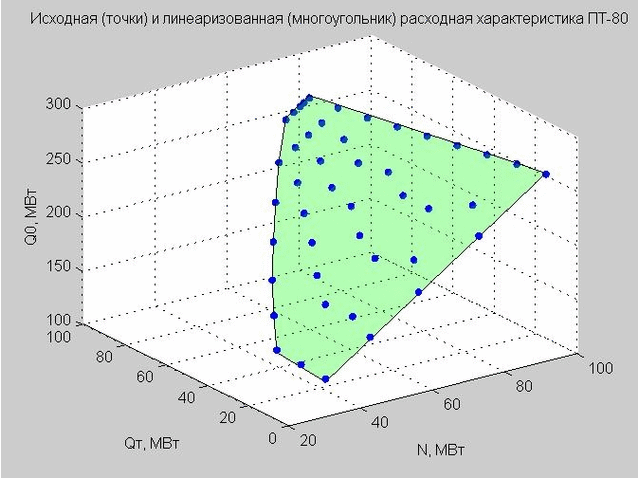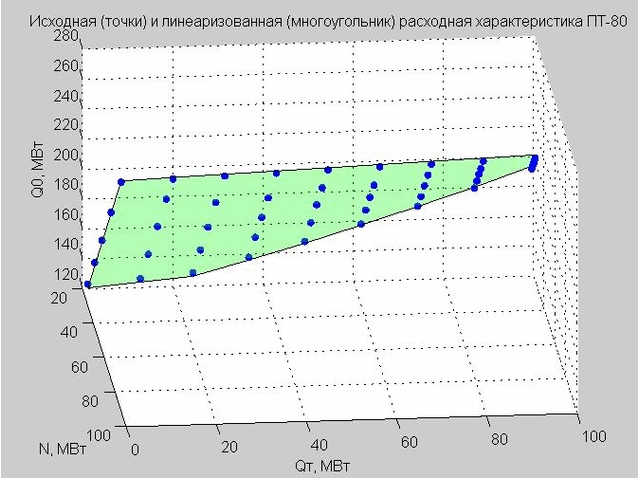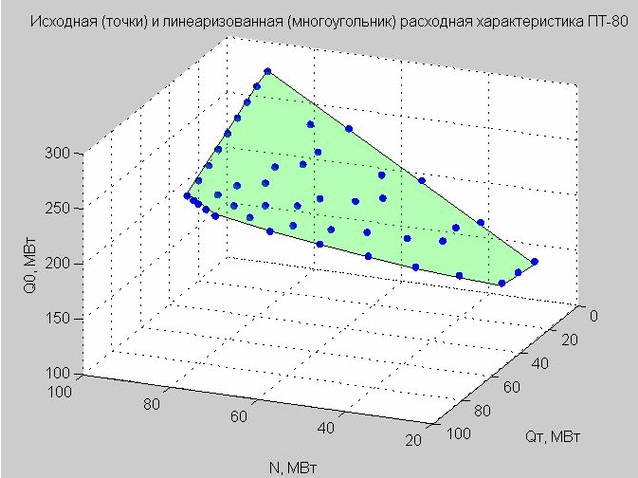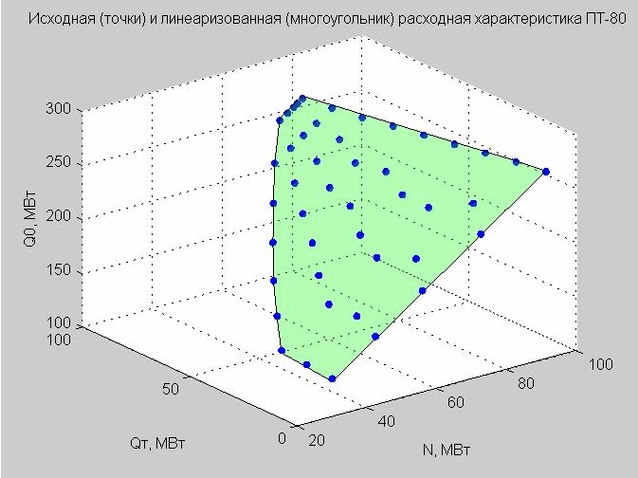
التين. 4. نقاط انطلاق خاصية التفريغ (النقاط الزرقاء) ، خاصية التفريغ الخطي (المضلع الأخضر المسطح)
دعونا نعود إلى صيغة خاصية معدل التدفق الخطي (4) التي حصلنا عليها. إذا قمنا بإصلاح Q p = 40 MW MW ، فستكون الصيغة هي النموذج
$$ display $$ \ start {equation} Q_0 = 2.317 \ cdot N + 0.255 \ cdot Q_T + 58.714 \ qquad (6) \ end {equation} $$ display $$
يحدد هذا النموذج مضلعًا مسطحًا في مساحة ثلاثية الأبعاد بالمحاور x - N، y - Q t ، z - Q 0 عن طريق القياس مع توربين من النوع T (نراه في الشكل 4).
قبل سنوات عديدة ، عندما تم تطوير q nomograms ، حدث خطأ أساسي في مرحلة تحليل البيانات الأولية. بدلاً من تطبيق طريقة المربعات الصغرى وبناء خاصية تدفق خطية للتوربين البخاري لسبب غير معروف ، قاموا بحساب بدائي:
$$ display $$ \ start {equation} Q_0 (N) = Q_ = Q_0 - Q_ - Q_ \ qquad (7) \ end {equation} $$ display $$
مطروح من معدل تدفق البخار عالي الضغط Q 0 معدل تدفق الأبخرة Q t و Q p وعزا الفرق الناتج Q 0 (N) = Q e لتوليد الكهرباء. تم الحصول على القيمة التي تم الحصول عليها Q 0 (N) = Q e على N وتم تحويلها إلى kcal / kW · h ، بعد أن تلقت إجمالي استهلاك معين q t . لا يتوافق هذا الحساب مع قوانين الديناميكا الحرارية.
أعزائي القراء ، ربما تعرف السبب غير المعروف؟ شاركه!
2. توضيح نطاق التعديل للتوربين البخاري
دعونا نرى قذيفة نطاق التعديل في مساحة النظام. يتم عرض نقاط البداية الخاصة ببنائه في الشكل. 5. هذه هي نفس النقاط التي نراها في الشكل. 3 ، ومع ذلك ، تم استبعاد المعلمة Q 0 الآن.

التين. 5. نقاط الانطلاق لخصائص التدفق في فضاء النظام بالمحاور x - N، y - Q p ، z - Q t
العديد من النقاط في الشكل. 5 محدب. باستخدام الدالة convexhull () ، حددنا النقاط التي تحدد الغلاف الخارجي لهذه المجموعة.
تسمح لنا Delaunay triangulation (مجموعة من المثلثات المتصلة) بإنشاء غلاف نطاق التعديل. رؤوس المثلثات هي القيم الحدية لنطاق تعديل التوربين البخاري PT-80 قيد النظر.
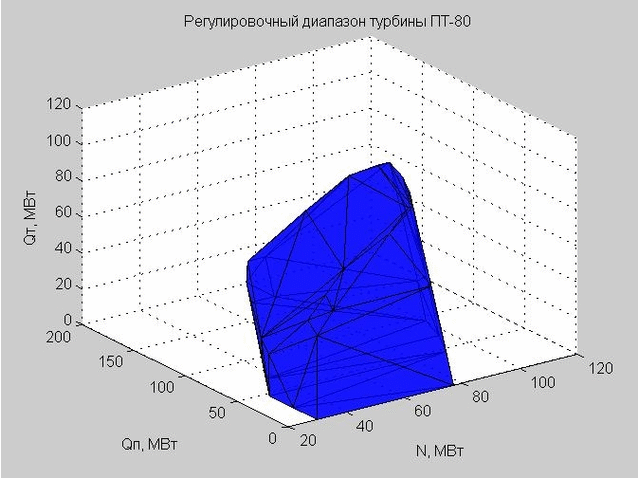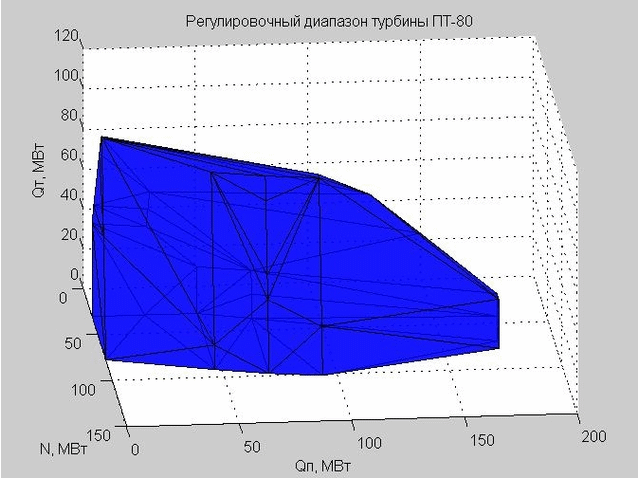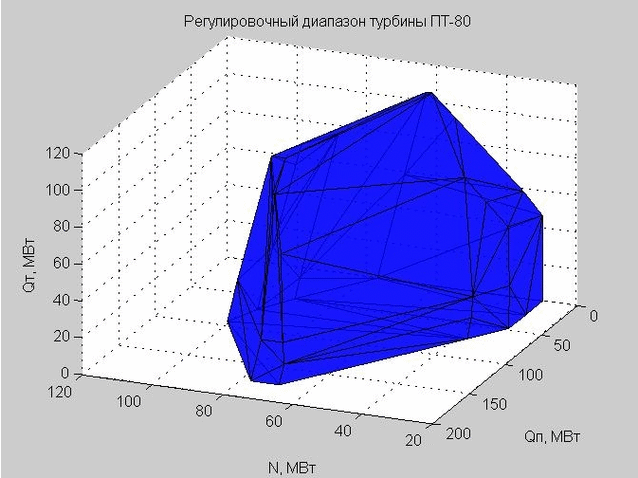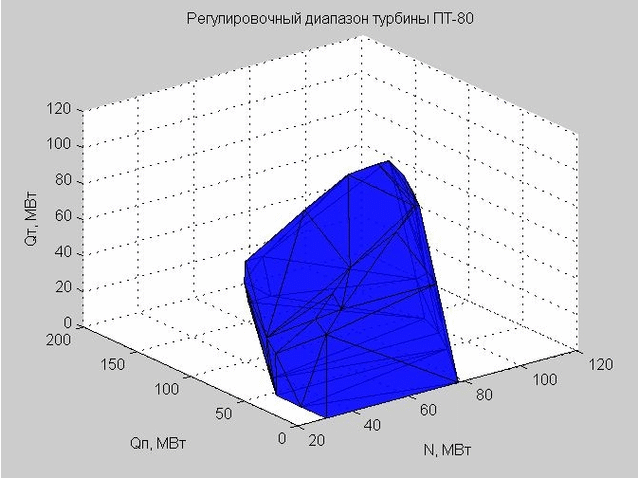
التين. 6. قذيفة نطاق التعديل ، ممثلة بالعديد من المثلثات
عندما قمنا بفحص نقطة معينة للوصول إلى داخل نطاق الضبط ، تحققنا مما إذا كانت هذه النقطة تقع داخل أو خارج الصدفة الناتجة.
تم إنشاء جميع الرسوم البيانية المعروضة أعلاه باستخدام أدوات MATLAB (انظر PT_80_linear_characteristic_curve.m).
مهام واعدة تتعلق بتحليل تشغيل التوربين البخاري باستخدام خاصية التدفق الخطي
إذا كنت تقوم بدبلومة أو أطروحة ، يمكنني أن أقدم لك العديد من المهام ، التي يمكنك إثبات جدوتها العلمية بسهولة للعالم كله. بالإضافة إلى ذلك ، ستقوم بعمل ممتاز ومفيد.
المهمة 1
بيّن كيف يتغير المضلع المسطح عندما يتغير ضغط بخار الضغط المنخفض Q t .
المهمة 2
بيّن كيف يتغير المضلع المسطح عندما يتغير الضغط في المكثف.
المهمة 3
تحقق مما إذا كان يمكن تمثيل معاملات خاصية التدفق الخطي كوظائف لمعلمات إضافية للنظام ، وهي:
$$ display $$ \ start {equation} \ alpha_N = f (p_ {0}، ...)؛ \\ \ alpha_P = f (p_ {P}، ...) ؛ \\ \ alpha_T = f (p_ {T}، ...) ؛ \\ \ alpha_0 = f (p_ {2} ، ...). \ إنهاء {المعادلة} $$ display $$
هنا p 0 - ضغط بخار عالي الضغط ، p p - ضغط بخار متوسط الضغط ، p t - ضغط بخار منخفض الضغط ، p 2 - ضغط بخار العادم في المكثف ، جميع الوحدات كجم / سم 2.
تبرير النتيجة.
المراجع
Chuchueva I.A. ، Inkina N.E. تحسين CHP في ظروف سوق الجملة للطاقة الكهربائية وقدرة روسيا // العلوم والتعليم: الطبعة العلمية من MSTU. N.E. بومان. 2015. رقم 8. س 195-238.
Chuchueva I.A. الطرق الحسابية لتحديد الاستهلاك المحدد للوقود المكافئ لمحطات الطاقة الحرارية للطاقة الكهربائية والحرارية الموردة في وضع التوليد المشترك // العلوم والتعليم: النشر العلمي لـ MSTU. N.E. بومان. 2016. رقم 2. ص 135-165.
خاصية التدفق الخطي للتوربين البخاري.