الكتلة والطاقة والزخم وقانون الحفظ

ترتبط العديد من الخصائص الغامضة للعالم بطبيعة الكتلة والطاقة (وكذلك الزخم). سمعنا جميعًا هذه الكلمات ، والعديد منا لديه فكرة غامضة عن معناها. وبطبيعة الحال ، فإن معاني الكلمتين "طاقة" و "طاقة" في اللغة الإنجليزية ولغات أخرى كثيرة. لسوء الحظ ، لا يتطابق أي منها مع تلك التي يفكر فيها الفيزيائيون. حاول أن تنحي معاني الكلمات هذه وأن تتعامل مع المفاهيم الجسدية الدقيقة - وإلا فسوف تشعر بالارتباك التام.

وتجدر الإشارة إلى أنه لا يجب على المرء أن يتذكر زوجًا شائعًا آخر ، "الجوهر والطاقة" مع عبارة "الكتلة والطاقة". يذكر الكثير من الناس العبارة الأخيرة كما لو كانت المادة والطاقة وجهان لعملة واحدة. لكن الأمر ليس كذلك. تندرج المادة والطاقة في فئات مختلفة ، مثل التفاح و الأورانجوتان. المادة ، بغض النظر عن كيفية تعريفها ، هي فئة من الكائنات الموجودة في الكون ، والكتلة والطاقة ليست أشياء ، ولكن الخصائص التي تمتلكها هذه الأشياء. تتشابك الكتلة والطاقة بشدة مع بعضها البعض ، وتستحق شرحًا عامًا.

لفهم الكتلة والطاقة ، تحتاج إلى إضافة زخم لهم ومناقشة الاختلافات والعلاقات بين هذه الكميات.

الطاقة

كلمة "طاقة" لها معاني عديدة. عندما نمرض ، نقول أنه لم يعد لدينا طاقة ، في إشارة إلى القوة والتحفيز. عندما نقول أن شخصًا ما مليء بالطاقة ، فإننا نعني نشاطه العالي. نشكو من ارتفاع أسعار الطاقة ، مشيرا إلى الوقود. نحن نتحدث عن الطاقة الروحية كشيء لا يقاس ، ولكنه مهم ، وربما شكل من أشكال الكاريزما. وكل هذه المفاهيم تتداخل مع بعضها البعض ، لذلك نختار كلمة واحدة لوصفها. لكن في الفيزياء الطاقة شيء مختلف تمامًا. من وجهة نظر الفيزياء ، سيتم الخلط بين واحد من هذه التعريفات عن طريق الخطأ مع المادية. في الفيزياء ، يجب على المرء الالتزام بمصطلح مادي حتى لا يحصل على إجابات خاطئة ولا يتم الخلط تمامًا.

لسوء الحظ ، يصعب وصف مفهوم "الطاقة" في الفيزياء كما تفعل القواميس - بعبارة قصيرة ذات معنى. لكن لا تفكر بالسوء - الأمر برمته هو النقص في اللغة الطبيعية ، وليس أن مفهوم الطاقة في الفيزياء غامض. في أي نظام مادي معين ، من الواضح تمامًا ماهية طاقته ، سواء من حيث القياس التجريبي أو بمعنى الحسابات (إذا كانت هناك معادلات تصف النظام).

أحد أسباب صعوبة وصف الطاقة هو أنها يمكن أن تتخذ أشكالًا عديدة ، وليس من السهل فهمها جميعًا. فيما يلي ثلاثة أصناف شائعة:

1. يمكن وضع الطاقة في كتلة جسم ما. هنا أسمي هذا الخيار "طاقة الكتلة" (بفضل المعادلة المعروفة E = mc ^{2 ،} ترتبط الطاقة بالكتلة. وتسمى أيضًا "طاقة الراحة" ، لأن هذه طاقة جسم في حالة استراحة ، أي بدون حركة).

2. ثانياً ، ترتبط الطاقة بحركة الجسم. هنا أسميها "طاقة الحركة" ، والمصطلح التقني لذلك هو الطاقة الحركية. هذا الخيار سهل الفهم بشكل بديهي ، لأن الأشياء سريعة الحركة لديها طاقة أكبر من تلك التي تتحرك ببطء. بالإضافة إلى ذلك ، يمتلك الجسم الثقيل طاقة حركة أكبر من الجسم الخفيف الذي يتحرك بنفس السرعة.

3. يمكن تخزين الطاقة في علاقة الأشياء (وتسمى عادة "المحتملة"). يتم تخزينه في زنبرك ممتد ، في الماء خلف السد ، في تفاعل الجاذبية للأرض والشمس ، في تفاعلات الذرات في الجزيء. هناك طرق عديدة لتخزين الطاقة. يبدو غامضًا ، لكن اللغة هي المسؤولة. في أي من هذه الحالات ، هناك صيغ دقيقة تصف الطاقة المخزنة في النظام وطرق محددة جيدًا لقياسها.

النوع الثالث من الطاقة مرتبط بما أسميه طاقة التفاعل ، وهذا هو المفهوم الأكثر إرباكًا على الإطلاق. على عكس طاقة الكتلة وطاقة الحركة ، التي تكون دائمًا أكبر من أو تساوي الصفر ، فإن طاقة التفاعلات يمكن أن تكون إيجابية وسلبية. سأترك هذا الموضوع حتى الآن ، ولكننا سنعود إليه.

الطاقة هي كمية خاصة ذات أهمية كبيرة للفيزياء. والسبب في هذه الأهمية هو أنها "محفوظة". ماذا يعني هذا؟

إذا بدأت الملاحظة بشيء أو بمجموعة من الأشياء - سنطلق عليها "نظام الأشياء" - تمتلك كمية معينة من الطاقة في اللحظة الأولى (لا تنس أن تحسب كل الطاقة - الكتل ، الحركات ، الطاقة المخزنة من جميع الأنواع ، وما إلى ذلك) ، ثم سوف تتفاعل أجزاء من النظام مع بعضها البعض فقط ومع أي شيء آخر ، ثم في نهاية الملاحظة سيكون إجمالي كمية الطاقة التي تمتلكها هذه الأشياء هي نفسها كما في البداية. يتم الحفاظ على الطاقة الإجمالية للنظام - لا يتغير إجمالي كميته. يمكن أن يتغير شكله ، ولكن إذا تابعت جميع الأصناف ، فعندئذٍ سيكون في النهاية كما هو الحال في البداية.

تعمل هذه القاعدة حتى إذا اختفت بعض الأشياء وتفسحت المجال للآخرين ، على سبيل المثال ، إذا تحلل جسيم واحد في النظام إلى جزأين آخرين اندمجا في النظام.

لماذا يتم توفير الطاقة؟ بسبب المبدأ الرياضي ، ربط حقيقة أن قوانين الطبيعة لا تتغير بمرور الوقت ، مع وجود كمية محفوظة ، والتي نسميها بحكم تعريفها "الطاقة".

نحن مدينون للتعريف الأكثر شهرة وعامة لهذا المبدأ لإيمي نويثر ، أحد أعظم علماء الفيزياء الرياضية في القرن السابق ، وهو معاصر لأينشتاين. عاملها بعض أعضاء المجتمع البدني والرياضي باحترام عميق ، ولكن في ذلك الوقت عانت ألمانيا في بلدها الأصلي من التمييز على أساس الجنس والجنسية (هناك منعوا محاولات تعيينها لقب أستاذ في غوتنغن ، ومن هناك اضطرت إلى الفرار بعد ذلك جاء النازيون إلى السلطة). بعد الهجرة إلى الولايات المتحدة ، بعد عامين فقط من التدريس في كلية برين مار (التي لا تقبل حتى الآن سوى النساء للتدريب) ، توفيت بسبب السرطان.

تخبرنا نظرية نويثر الشهيرة (في الواقع هاتان نظريتان مرتبطتان ارتباطًا وثيقًا) أنه إذا كان هناك تناظر في قوانين الطبيعة - في حالتنا ، فهذا يعني أن قوانين الطبيعة هي نفسها في أي لحظة من الزمن - فهذا يحافظ على كمية معينة - في حالتنا ، الطاقة .

علاوة على ذلك ، تخبرنا النظرية بالضبط ما هو الحجم - ما هي أشكال الطاقة المختلفة لنظام معين من الأشياء التي يجب إضافتها من أجل الحصول على الطاقة الإجمالية. هذا هو السبب في أن الفيزيائيين يعرفون دائمًا ما هي الطاقة بالضبط ، ولماذا يكون الحصول على المعادلات أسهل من التعريف في الكلمات.

الاندفاع

الوضع مع الزخم هو نفسه تقريبا مع الطاقة. قوانين الطبيعة هي نفسها في كل مكان. بشكل تقريبي ، تعطي التجارب نفس الإجابات ، سواء كنت تنفقها شمالًا أو جنوبًا هنا ، غربًا أو شرقيًا ، فوق مبنى أو في عمود عميق. اختر أي اتجاه في الفضاء. ثم ، وفقًا لـ Noether ، يتم الحفاظ على الزخم على هذا الاتجاه. نظرًا لوجود ثلاثة أبعاد في الفضاء ، فمن الممكن التحرك في ثلاثة اتجاهات مستقلة مختلفة وهناك ثلاثة قوانين حماية مستقلة. يمكنك اختيار أي ثلاثة اتجاهات ، شريطة أن تكون مختلفة. على سبيل المثال ، يمكنك اختيار النبضات في الاتجاهات بين الشمال والجنوب والغرب الشرقي والصعود كأعلى قوانين للحفظ. أو يمكنك اختيار ثلاثة آخرين - في الاتجاه من الشمس وإليها ، على مدار مدار الأرض في كلا الاتجاهين ، ولأعلى ولأسفل فيما يتعلق بمستوى النظام الشمسي. لا يهم اختيارك ، لأنه يتم تخزين الزخم على طول أي اتجاه.

ينشأ أبسط شكل من أشكال الدفع بسبب الحركة البسيطة للأشياء ، وهذا شيء يمكن تخيله بشكل حدسي: إذا كان الجسم يتحرك في اتجاه معين ، فعندئذ يكون لديه دافع في هذا الاتجاه ، وكلما أسرع في التحرك ، زاد هذا الدافع. والجسم الأثقل لديه زخم أكبر من الضوء إذا تحرك بنفس السرعات.

إحدى النتائج المثيرة للاهتمام لهذا الحفظ: إذا كان لديك نظام من الأشياء بدون حراك (أي أن النظام ككل لا يتحرك إذا قمت بتوسيط جميع حركات الأشياء المكونة له) ، فسيبقى بلا حراك ، ما لم يتم منحه أي حركة خارجية تأثير. والسبب هو أنه في النظام الثابت ، يكون الزخم الإجمالي صفرًا ، وبما أن الزخم محفوظًا ، فسيظل صفرًا إلى الأبد ما لم يتدخل شيء من خارج النظام.

الكتلة وعلاقتها بالطاقة والزخم

الآن دعونا ننتقل إلى الكتلة

لسوء الحظ ، يرتبط الكثير من الارتباك بالكتلة - بعد نشر عمل أينشتاين حول نظرية النسبية لبعض الوقت كان هناك مفهومان للكتلة. واحد منهم فقط (الذي توقف عليه أينشتاين نفسه ، والذي يطلق عليه أحيانًا "الكتلة الثابتة" أو "الكتلة الباقية" لتمييزه عن المصطلح القديم الذي أصبح بالفعل "الكتلة النسبية") ، لا يزال يستخدم في فيزياء الجسيمات. في مقال منفصل سأشرح هذا بمزيد من التفصيل.


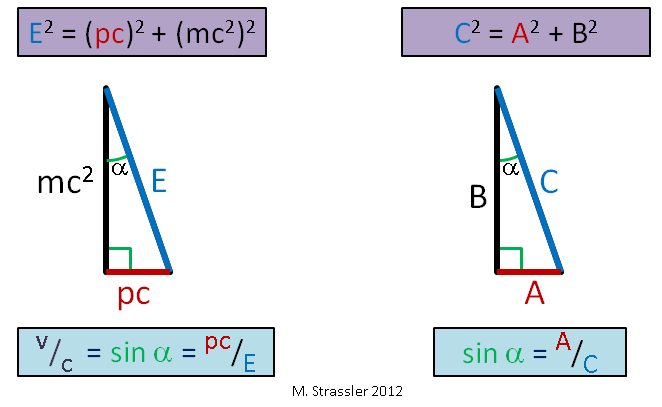
التين. 1

تعني الكتلة m ، التي أستخدمها في المقالات ، أن الكتلة التي تربط الطاقة والزخم بشكل مباشر. بالنسبة لجسم يتحرك بدون تأثير القوى الخارجية (لا يتفاعل بشكل كبير مع الأشياء الأخرى) ، اقترح آينشتاين (وهذا ما أكدته التجارب) أن طاقته E ، والزخم p ، والكتلة m ترضي المساواة فيثاغورس البسيطة:

$$

$$E ^ 2 = (p c) ^ 2 + (mc ^ 2) ^ 2 \ qquad (المعادلة رقم 1)$$

تذكروا فيثاغورس القديمة الذين ادعوا أنه بالنسبة للمثلث الأيمن مع الجانبين A و B والوتر C ، فإن المساواة $$$C ^ 2 = A ^ 2 + B ^ 2$ ؟؟؟ هذا اتصال من نفس النوع - انظر الشكل. 1. معنا ، c هي سرعة ثابتة ، والتي ، كما سنرى ، بمثابة الحد الأقصى للسرعة العالمية. سنرى أيضًا سبب تسميتها "سرعة الضوء".

وفقًا لمعادلات آينشتاين ، فإن سرعة الجسم مقسومة على حد السرعة c هي فقط نسبة الكمبيوتر إلى E:

$$

$$v / c = (p c) / E \ qquad (المعادلة رقم 2)$$

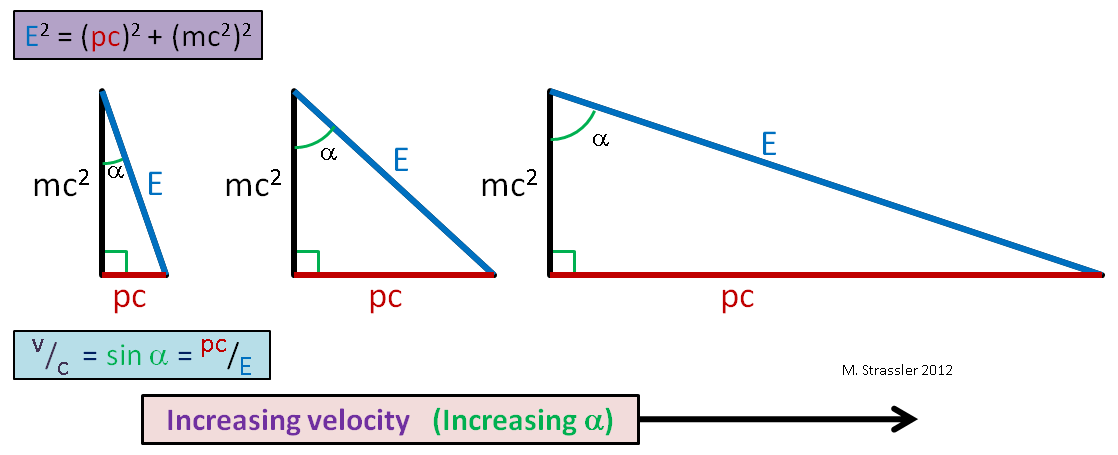
أي نسبة الساق الأفقية إلى الوتر. كما أنها تساوي جيب الزاوية α في الشكل. 1. حتى هنا أيها المواطنون. وبما أن أرجل مثلث قائم الزاوية دائمًا أقصر من الوتر (جيب أي زاوية يكون دائمًا أقل من أو يساوي 1) ، لا يمكن أن تتجاوز سرعة أي كائن s ، الحد الأقصى للسرعة العالمية. مع زيادة سرعة كائن ذي كتلة ثابتة ، يصبح p و E كبيرًا جدًا (الشكل 2) ، لكن E دائمًا ما يكون أكبر من جهاز الكمبيوتر ، لذا فإن v دائمًا أقل من c!


التين. 2

لاحظ الآن أنه إذا لم يتحرك الجسم ، فإن زخمه p يساوي صفر ، وتقل النسبة في المعادلة 1 إلى:

$$

$$E ^ 2 = (mc ^ 2) ^ 2 ، \ quad or \ quad E = mc ^ 2$$

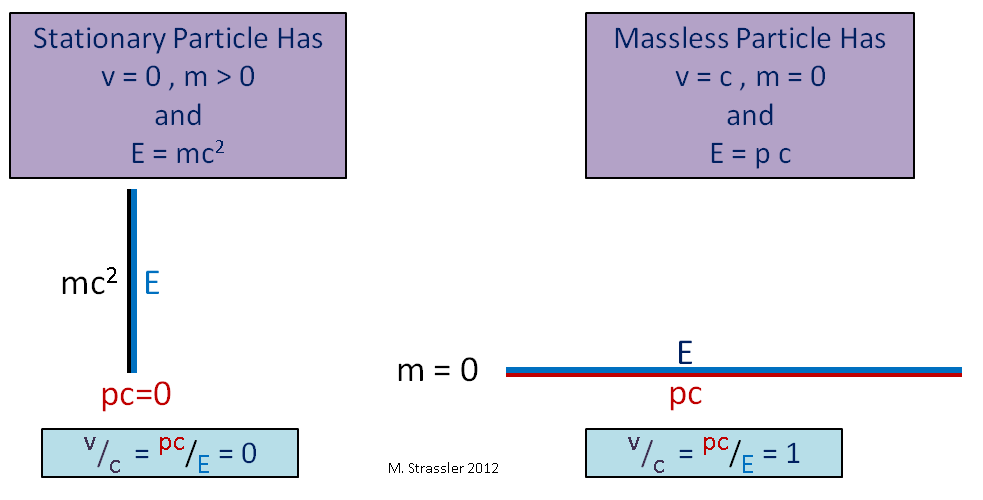
صيغة آينشتاين الشهيرة ، علاقة الكتلة بكمية ثابتة من الطاقة (ما أسميه طاقة الكتلة) ، هي ببساطة عبارة تتوافق مع حقيقة أنه عندما يتحول المثلث إلى خط رأسي ، كما هو الحال في الشكل. 3 على اليسار ، يصبح الوتر بنفس طول الساق الرأسية. في الوقت نفسه ، لا يعني ذلك أن الطاقة تساوي دائمًا كتلة الكتلة من مربع s. هذا يعمل فقط لكائن يستريح بدون زخم.


التين. 3

ملاحظة أخرى مثيرة للاهتمام: بالنسبة للجسيمات عديمة الكتلة ، تكون الساق الرأسية للمثلث صفرًا ، والوتر والساق الأفقية هي نفسها ، كما في الشكل. 3. في هذه الحالة ، E هو جهاز كمبيوتر ، مما يعني أن v / c = 1 ، أو v = c. يُلاحظ أن الجسيم عديم الكتلة (على سبيل المثال ، الفوتون ، جسيم الضوء) يتحرك حتمًا بسرعة c. لذلك ، فإن سرعة الضوء هي نفس سرعة السرعة العالمية ، s.

من ناحية أخرى ، إذا أخذنا جسيمًا مع الكتلة ، كما في الشكل. 4 ، لا يهم حجم حجم الزخم والطاقة ، ستظل E دائمًا أكثر بقليل من p * c ، لذلك ستكون السرعة دائمًا أقل من s. يجب أن تتحرك الجسيمات عديمة الكتلة بأقصى سرعة. يجب أن تكون سرعة الجسيمات الضخمة أقل.


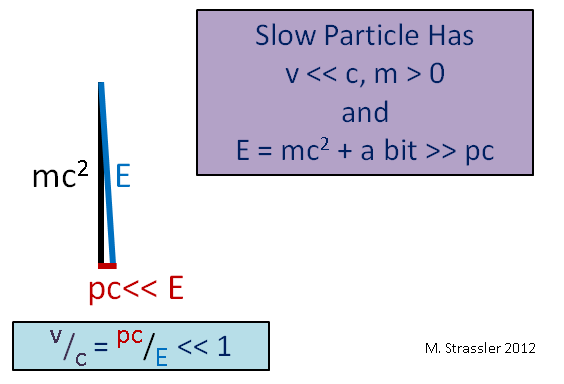
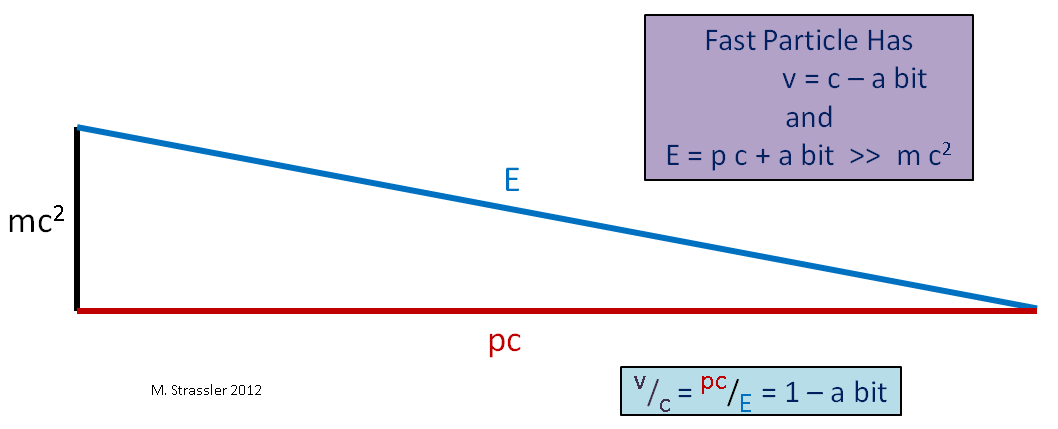التين. 4. هنا ">>" تعني "أكثر بكثير"

تخيل حالة حدودية أخرى ، جسم ضخم يتحرك ببطء (مقارنة بسرعة الضوء) ، مثل سيارة. نظرًا لأن سرعته v أقل بكثير من c ، فإن زخمه p مضروبًا في c سيكون أقل بكثير من E ، وكما يتضح من الشكل. 5 ، E سيكون أكثر بقليل من mc ² . لذلك ، فإن طاقة حركة الجسم البطيء E - mc ² أقل بكثير من طاقة كتلته mc ² ، وبالنسبة للجسم السريع ، يمكن جعل طاقة الحركة كبيرة بشكل تعسفي ، كما رأينا في الشكل. 4.

نقطة واحدة خفية: الزخم ليس مجرد رقم ، ولكنه أيضًا ناقل. لديه الحجم والاتجاه. إنه موجه نحو حركة الجسيم. عندما أكتب p ، فأنا أشير فقط إلى القيمة. في كثير من الحالات ، من الضروري تتبع اتجاه النبض ، على الرغم من أن ذلك ليس ضروريًا في المعادلة رقم 1 ، التي تربط النبض بالطاقة والكتلة.


التين. 5

نقطة أخرى خفية: استخدمت المثلثات وعلم المثلثات البسيط ، لأنها معروفة للجميع من المدرسة. يحتاج الخبراء إلى أن يكونوا أكثر حذراً - يمكنك فهم معادلات آينشتاين بشكل صحيح باستخدام الدوال الزائدية التي لا يجدها الهواة عادة ، ولكنها مهمة للغاية لفهم هيكل النظرية وجعل الأمور أكثر قابلية للفهم مثل إضافة السرعة ، وضغط المسافة ، وما إلى ذلك. يمكن للأشخاص الذين لا يدعون أنهم خبراء أن يتجاهلوا ذلك.

ولكن هل السرعة نسبية؟ ..

إذا قرأت النص بعناية ، فقد يفاجئك شيء بالفعل. أنت تعلم أن سرعة الجسيم - أو أي شيء يتحرك أبطأ من الضوء - يعتمد على وجهة النظر.

إذا كنت تجلس في المنزل وقرأت كتابًا ، فستقول أن سرعة الكتاب صفر (وهي في الحقيقة مرتبطة بك) ، وبالتالي ، ليس لديها زخم وطاقة الحركة ، فقط طاقة الكتلة. ولكن إذا وقفت على القمر ، فسأذكرك أن الأرض تدور ، لذا فإن هذا الدوران يأسرك ، وينقلك بالنسبة لي بسرعة مئات الكيلومترات في الساعة. لذا أنت وكتابك سيكون لديك الدافع من وجهة نظري.

من على حق؟

متغير النسبية وفقا لغاليليو - مبدأ النسبية الأول - ينص على أننا على حق. يتفق متغير النسبية لأينشتاين مع وجهة نظر غاليليو بأن كلاهما على حق ، لكنه يقوم بتعديلات مهمة على كيفية إشارة أتباع غاليليو إلى طاقة وزخم وكتلة الكتاب ، مما يضع هذه الكميات في علاقة فيثاغورس للمعادلة رقم 1.

ولكن إذا كان كل شيء على ما يرام ، أي E وأي p أحتاج إلى استبداله في نسبة الطاقة / الزخم / الكتلة ، $$$E ^ 2 = (p c) ^ 2 + (mc ^ 2) ^ 2$ ؟؟؟ يقاس البديل E و p بقراءة الكتاب ، أي E = mc ² و p = 0؟ أو استبدل E و p ، الذي يحمله الكتاب من وجهة نظري ، عندما تتحرك مع الأرض؟

تحتوي الإجابة على هذا السؤال على جوهر معادلة آينشتاين رقم 1. سيقيس كل مراقب قيمًا مختلفة لـ E و p للكتاب ، اعتمادًا على مدى سرعة تحرك الكتاب بالنسبة إليه. ولكن لجميع المراقبين المعادلة $$$E ^ 2 = (p c) ^ 2 + (mc ^ 2) ^ 2$ سيكون صحيحا!

السحر! لكن في الواقع ، تعتبر العبقرية فكرة ظهرت في عام 1905 حول كيفية استبدال مجموعة المعادلات التي اقترحها نيوتن وأتباعه بمجموعة مذهلة جديدة من المعادلات ، والتي لا تزال تتزامن مع جميع التجارب السابقة ، ولكن تبين أنها تمثل تمثيلًا أكثر دقة للواقع. من الصعب تخيل كم كان من الضروري تغيير طريقة التفكير من أجل التفكير فيها حتى تكتشف مدى خطورة كل شيء أثناء تشكيل النظرية الجديدة ، وعدد المعادلات المختلفة الأخرى التي تحتوي على تناقضات مع الرياضيات أو التجارب السابقة ، يمكنك سيكون عرض (وعرض عليهم الناس). على سبيل المثال ، يأتي إليّ عمل الفيزيائيين المبتدئين باستمرار ، محاولين "إصلاح" معادلات أينشتاين ، لكنني لم أر أيًا منهم يفحص معادلاتهم من أجل الاتساق الداخلي. هذه مهمة صعبة للغاية وسبب فشل معظم النظريات.

ولكن كيف يمكن إذن الحفاظ على الطاقة والزخم؟

انتظر لحظة ، عندما تقول ، عندما يكون رأسك جاهزًا للانفجار ورش كل شيء من حولك بدماغك (أتذكر هذا الإحساس بنفسي) ، ولكن يجب الحفاظ على الطاقة والزخم! إذن كيف يمكن للمراقبين المختلفين أن يختلفوا مع ما هم عليه؟

هناك سحر أكثر ، بالمناسبة ، كان قبل آينشتاين. صدقوني ، الكون محاسب ذكي للغاية ، وعلى الرغم من حقيقة أن المراقبين المختلفين لن يوافقوا على الطاقة المتاحة في كائن أو نظام من الأشياء ، فإنهم سيتفقون جميعًا على أن هذه الطاقة لا تتغير مع مرور الوقت. وينطبق نفس الشيء على الزخم.

لكن الكتلة تختلف تمامًا عن الطاقة والزخم. أولا ، لا يتم حفظ الكتلة. في الطبيعة ، هناك العديد من العمليات التي تغير الكتلة الإجمالية للنظام: على سبيل المثال ، يمكن أن يتحلل جسيم هيجز الضخم إلى فوتونين بلا كتلة. لا يوجد تناظر مرتبط بالكتلة ، وبالتالي ليس لدى Noether قانون حماية لنا. ثانيًا ، على عكس الطاقة والزخم ، اللذين تعتمد قيمهما على المراقب (على وجه الخصوص ، على سرعته فيما يتعلق بالأجسام المقيسة) ، سيتفق جميع المراقبين على الكتلة m للجسم. وهذا ليس واضحًا على الإطلاق ، ويحدث ذلك لأن معادلات أينشتاين تعمل بشكل رهيب.

فماذا لدينا

في الوقت الحالي ، لدينا العديد من المعرفة المتضاربة للوهلة الأولى. نحن نعلم أن:

• يتم الحفاظ على طاقة وزخم النظام الفيزيائي المعزول (لا تتغير الطاقة الكلية والزخم الكلي لنظام معزول مع مرور الوقت) من وجهة نظر أي مراقب.
• سوف يقوم المراقبون المختلفون المتحركون بالنسبة لبعضهم البعض بتقييم قيم الطاقة وزخم النظام بشكل مختلف!
• لم يتم حفظ مجموع كتل الأشياء التي يتكون منها النظام ، يمكن أن يتغير.
• لكن جميع المراقبين يوافقون على كتلة الجسم.

يجب إضافة حقيقتين إضافيتين واستنتاجين إلى هذه القائمة:

كتلة النظام المادي للأشياء لا تساوي مجموع كتل الأشياء التي يتكون منها هذا النظام.

بدلاً من ذلك ، يتم تحديد كتلة النظام المادي ، التي يتفق عليها جميع المراقبين ، من خلال طاقتها وزخمها ، وتفي بنسختها من المعادلة رقم 1:

$$

$$(E_{system})^2 = (p_{system} c)^2 + (m_{system} c^2)^2 \qquad ( №1')$$

اتضح أن هناك حاجة إلى قانون إضافي للحفظ ، وأنه على الرغم من أن مجموع كتل الأشياء التي يتكون منها النظام غير محفوظ ، يتم الحفاظ على كتلة النظام ، لأنه مرتبط من خلال المعادلة رقم 1 `` بالطاقة وزخم النظام الذي يتم الحفاظ عليه.

كتلة نظام الأشياء هي العنصر الوحيد في قائمتنا الذي يتم الحفاظ عليه في وقت واحد ولا يخضع للنقاش من قبل المراقبين.

ما عليك سوى أن تتذكر أن كتلة نظام الأجسام ليست مجموع كتل الأجسام التي يتكون منها النظام ، بل ما تعنيه المعادلة رقم 1.

من محاولة شرحه ، انظر فقط كيف يعمل. مثال حي يساوي ألف كلمة. دعنا نأخذ كمثال لنظام أكثر شيء عصري ، أي جسيم هيجز (لديه كتلة 126 GeV / s ² ) ، وانظر كيف تعمل العبارات المختلفة المذكورة أعلاه عندما تتحلل إلى فوتونين.

جسيم هيجز واحد ، وفوتونان وثلاثة مراقبون

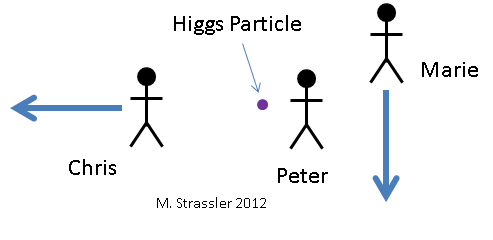التين. 6. ينظر ثلاثة مراقبين إلى جسيم هيجز. فيما يتعلق بها ، لا يتحرك بيتيا (بيتر) ، يتحرك ماشا (ماري) لأسفل ، وينتقل كوستيا (كريس) إلى اليسار.

دعونا نلقي نظرة على كيفية انحلال جسيم هيجز إلى فوتونين ، من وجهة نظر ثلاثة مراقبين مختلفين. وتظهر في الشكل. 6 جنبًا إلى جنب مع جسيم هيجز الذي ينظرون إليه. بالطبع ، لا يمكنهم رؤيتها من خلال العيون ، لأنها لا تملك سوى وقت قليل جدًا وهي صغيرة جدًا. يحتاجون إلى استخدام نوع من المعدات العلمية. بالنسبة لبيتيت ، لا يتحرك جسيم هيجز. يتحرك ماشا إلى أسفل بالنسبة لبيتيت. تحرك Kostya يسارًا بالنسبة إلى Petit. لذا ، بالنسبة لماشا ، يتحرك جسيم هيجز لأعلى ، وللعظام - إلى اليمين. يرى ثلاثة مراقبين كيف يتحلل الجسيم وفقًا للشكل. 7. يرى بيتيا أن هيغز يتحلل إلى فوتونين بنفس الطاقة ، أحدهما يتحرك للأعلى والآخر للأسفل. يرى ماشا أن هيجز يتحلل إلى فوتونين من طاقات مختلفة ، وأن الطاقة المتحركة للأعلى لديها طاقة أكثر من الطاقة المتحركة للأسفل.يرى Kostya انحلال Higgs إلى فوتونين يتجهان يمينًا ويسارًا. دعونا نحسب الطاقات والعزم المعينين إلى هيجز وفوتون من قبل المراقبين ، وكيف سيصل كل واحد منهم إلى استنتاج مفاده أن الطاقة والزخم يتم الحفاظ عليهما خلال الاضمحلال.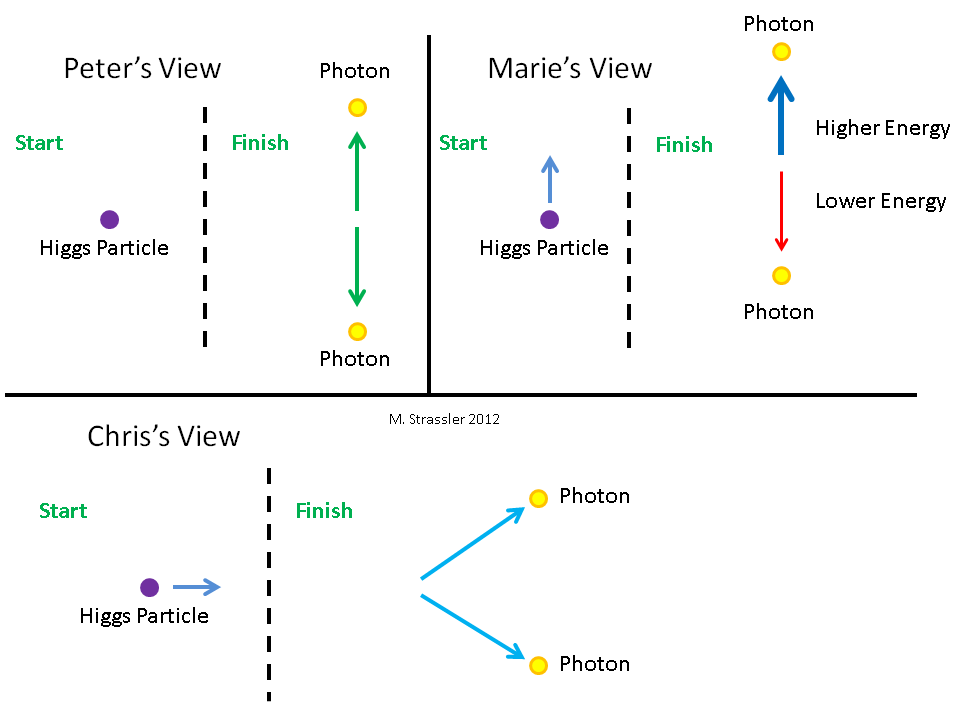

تحلل جسيمات هيجز

أولاً ، نقوم بتحليل جسيم هيجز من وجهة نظر بيتيت. ينظر بتيا (باستخدام أدوات قياس) إلى جسيم هيجز ، وماذا يرى؟ (سأضع اندفاعة حول كل ما يراه بيتيا ، ثم نقارن ذلك بملاحظات ماشا وكوستيا). هيجز لا يتحرك ، لذا زخمه$$$\overline{p_0}$تساوي صفر ، ووفقًا للمعادلة رقم 1 ، مع كتلته m = 126 GeV / c ^{2 ،} ستكون الطاقة$$$\overline{E_0} = m c^2 = 126$

الآن ، وفقًا للحفاظ على الطاقة والزخم ، سيحافظ نظام يتكون من جسيم هيجز على كل الطاقة والزخم بعد الاضمحلال. وسيظل الأمر كذلك حتى لا تؤثر قوة خارجية على هيجز. قد تسأل ما إذا كنا بحاجة إلى القلق بشأن الجاذبية ، لأن الجاذبية ستكون تأثيرًا خارجيًا يمكن أن يغير الزخم. إجابتي هي أنه في الوقت القصير الذي يتحلل فيه هيجز ، سيكون تأثير الجاذبية صغيرًا جدًا لدرجة أنه إذا أخبرتك كم هو صغير حقًا ، فستضحك. إنسى الأمر

لذلك ، عندما يتحلل هيجز ، يجب أن يبلغ إجمالي طاقات الجسيمات التي تشكل بقاياها 126 غيغابايت ، وزخم الجسيمات (بالنظر إلى أن الزخم ليس فقط كمية ، ولكن أيضًا اتجاه - متجه) سيصل إلى الصفر.

يمكن للفوتونات عديمة الكتلة التي يتحلل فيها هيجز أن تتناثر في أي اتجاه ، ولكن لتبسيط المثال ، تخيل أنها تتناثر عموديًا - واحد لأعلى والآخر ، يرتد عنه ، إلى أسفل. (بعد ذلك بقليل سنناقش لماذا يجب أن يطيروا في اتجاهين معاكسين).

ما الزخم الذي تملكه الفوتونات؟ إنه بسيط. أولاً ، يجب أن يكون الزخم الكلي للنظام - مجموع العزم من فوتونين - صفرًا ، لأن هيجز كان لديه زخم صفري قبل الاضمحلال (من وجهة نظر بيتي). الآن كل من الفوتونات لديه دفعة بقوة واتجاه معين. في المجموع ، يمكن أن تعطي صفرًا بطريقة واحدة فقط - إذا كانت متساوية في الحجم وفي الاتجاه المعاكس. إذا ارتفع أحدهما ، يجب أن ينخفض ​​الآخر ، ويجب أن يكون حجمهما هو نفسه.


التين. 8: ما يراه بيتيا

، ثانياً ، الطاقة الإجمالية للنظام هي مجموع طاقات فوتونات اثنين. هذا لأنه لا توجد طاقة تفاعلية بينهما (باستثناء جاذبية الجاذبية الصغيرة جدًا ، والتي يمكنك نسيانها). بالطبع ، بما أنه ليس لديهم كتل ، فإن كل طاقتهم تكون في طاقة الحركة. بالإضافة إلى ذلك ، في حالة الجسيمات عديمة الكتلة ، تقترح المعادلة رقم 1 أن E = pc ، حيث p هو الزخم. وبسبب هذا ، يجب أن يكون لدى فوتونين بنفس العزم نفس الطاقة. وبما أن هذين الطاقين يجب أن يضيفا إلى طاقة جسيم هيجز ، فإن طاقة كل فوتون يجب أن تساوي نصف طاقة جسيم هيجز.

$$

$$\overline E_1 = \overline E_2 = 1/2 (126 ) = 63$$

وبما أن الجسيم عديم الكتلة p = E / c ، إذن

$$

$$\overline p_1 = 63 /c \uparrow \\ \overline p_2 = 63 /c \downarrow$$

ويتم عرضها في الشكل. 8.

يتم الحفاظ على الطاقة والزخم ، ولكن الكتلة ليست كذلك ، لأن الفوتونات ليس لها كتلة ، كما فعل هيجز. ماذا عن كتلة النظام؟ ما هي كتلة نظام الفوتونين؟ غير صفري. من الواضح ما هي. بالطريقة نفسها كما في حالة هيجز نفسها (التي تألف منها النظام بأكمله في الأصل) ، فإن نظام من فوتونين له نفس الطاقة والزخم الذي كان له هيجز:

$$

$$E_{system} = \overline E_1 + \overline E_2 = 63 + 63 = 126 \\ p_{system} = \overline p_1 \uparrow + \overline p_2 \downarrow = 63 /c \uparrow + 63 /c \downarrow = 0$$

ومنذ ذلك الحين لبيتيت $$$p_{system} = 0$ ،

$$

$$m_{system} = E_{system} / c^2 = 126 /c^2$$

هذه هي كتلة هيجز. كتلة النظام لم تتغير خلال الاضمحلال ، كما هو متوقع.

المراقب الذي يتحرك هيجز لأعلى

تنتقل Masha إلى أسفل فيما يتعلق بـ Peta ، لذلك من وجهة نظرها ، تتحرك Petya و Higgs لأعلى. لنفترض أن Higgs يتحرك بسرعة v = 0.8 s ، أي 4/5 من سرعة الضوء بالنسبة إليها. على عكس بيتيا ، من وجهة نظر ماشا ، لدى هيجز زخم غير صفري ، وتبين أن عزم الفوتونات مختلف في الحجم ، ولكنه لا يزال متعدد الاتجاهات - ونتيجة لذلك سيكون مجموع عزمها غير صفري.


التين. 9: كيف يرى ماشا انحلال جسيم هيجز

كيف نحسب الزخم والطاقة التي يتمتع بها هيجز والفوتونان اللذان يتحللان فيهما ، من وجهة نظر ماشا؟ للقيام بذلك ، نحتاج إلى مجموعة أخرى من معادلات أينشتاين البسيطة. لنفترض ، من وجهة نظر مراقب معين ، أن الجسم لديه زخم p وطاقة E. ثم ، من وجهة نظر مراقب آخر يتحرك بسرعة v في اتجاه الجسم (أو ضده) ، سيتم التعبير عن زخم وطاقة الجسم على النحو التالي:

$$

$$p = γ (\overline p+ v \overline E/c^2) \qquad ( №3) \\ E = γ (\overline E + v \overline p) \qquad ( №4)$$

حيث γ يفي بمعادلة فيثاغورس أخرى:

$$

$$1 = v^2/c^2 + 1/γ^2 \qquad ( №5)$$

وفقا لأينشتاين. هذا يسمح لنا بإجراء التحولات بين ما يراه بيتيا وما يراه ماشا (أو أي مراقب آخر يتحرك بسرعة v). يظهر ما نجد في الشكل. 9.

لمقارنة ملاحظات ماشا مع ملاحظات بيتيا ، نحتاج إلى v و γ. أزعم أنه إذا v = 4/5 ج ، ثم γ = 5/3.

تحقق باستخدام المعادلة رقم 5: 1 = (4/5) 2 + (3/5) 2 = 16/25 + 9/25 = 25/25

يقول بيتيا أن في هيجز$$$p_0=0, E_0=126$ .ماذا عن ماشا؟ تقول:

$$

$$p_0 = γ v \overline E_0 = (5/3) (4/5) \overline E_0 = 168 /c \uparrow \\ E_0 = γ \overline E_0 = (5/3) \overline E_0 = 210$$

يدعي بيتيا أن اثنين من الفوتونات $$$\overline E_1 = \overline E_2 = 63$ولكل منهم E = p c. يمكننا الآن حساب ما يراه ماشا باستخدام المعادلتين رقم 4 ورقم 4.

$$

$$E_1= γ (1+v) \overline E_1 = 189 , p_1 = E_1/c \uparrow$$

$$

$$E_2= γ (1-v) \overline E_2= 21 , p_2 =E_2/c \downarrow$$

يعمل! كما يتم الحفاظ على الطاقة من وجهة نظر ماري ، ل

$$

$$E_0 = 210 \\ E_1 + E_2 = (189 + 21) = 210$$

يتم حفظ الاندفاع أيضًا:

$$

$$p_0 = 168 /c \uparrow \\ p_1 + p_2 = 189 /c \uparrow + 21 /c \downarrow = (189 – 21) /c \uparrow = 168 /c \uparrow$$

تتزامن كتلة النظام مع كتلة هيجز قبل وبعد الاضمحلال ، منذ قبل وبعد الاضمحلال

$$

$$E_system = 210 \\ p_system = 168 /c \uparrow$$

والتي ، حسب المعادلة رقم 1 ، تعيد كتلة النظام إلى الوراء $$$126 /c^2$ كما هو الحال مع بيتي ، لأنه

$$

$$210^2 = 168^2 + 126^2$$

المراقب من وجهة نظر هيجز التي تنتقل إلى اليمين

ماذا لدينا مع العظام؟ ينتقل Kostya إلى اليسار بالنسبة ل Petya ، على سبيل المثال ، بسرعة v = 4/5 ثانية ، بحيث يتحرك Higgs (و Petya) إلى اليمين فيما يتعلق بـ Kostya بسرعة v = 4/5 ثانية. نفس الحسابات التي أجريناها لماشا تظهر أن طاقة هيجز$$$E_0 = 210 GeV و p_0 = 168 GeV$ ولكن ، على عكس ماشا ، الذي يتحرك هيجز لأعلى ، بالنسبة لكوستيا ، يتم توجيه دافع هيجز إلى اليمين. هذا مبين في الشكل. 10.


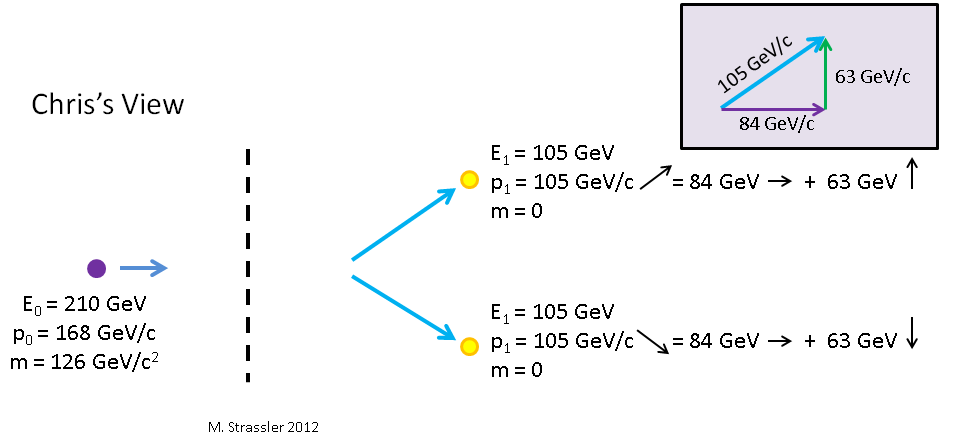
التين. 10

يتحلل هيجز إلى اثنين من الفوتونات. إذا تحركت الفوتونات صعودًا ونزولًا من وجهة نظر بيتيا ، فعندما يتحرك كوستيا ، الذي يشاهد هيغز وبيتيا ، إلى اليمين ، يتحرك أحد الفوتونات إلى اليمين وينتقل الآخر إلى اليمين. ما الدافع والطاقة التي سيحصلون عليها بعد ذلك؟

من خلال المعادلتين رقم 4 ورقم 5 لا نعرف ذلك ، لأنه مخصص للحالات التي يتحرك فيها الجسيم والمراقب في نفس الاتجاه. بالنسبة لحالتنا ، ستكون المعادلات على النحو التالي:

$$

$$\ updownarrow p = \ updownarrow \ overline p \\ \ leftrightarrow p = γ ([\ leftrightarrow \ overline p] + v \ overline E / c ^ 2) \\ E = γ (\ overline E + v [\ leftrightarrow \ خط ع]]$$

ستكون هذه المعادلات أبسط مما تبدو عليه ، لأنه من وجهة نظر Petit ، لا تحتوي p على مكون يتحرك من اليسار إلى اليمين ، والنبضة بأكملها ترتفع أو تنخفض. لذا يلاحظ Kostya القيم التالية لـ Higgs:

$$

$$\ updownarrow p_0 = \ updownarrow \ overline p_0 = 0 \\ \ leftrightarrow p_0 = γ v \ overline {E_0} / c ^ 2 = (5/3) (4/5) 126 GeV / c = 168 GeV / c \ rightarrow \\ E = γ \ overline {E_0} = (5/3) 126 GeV = 210 GeV$$

ويصعد الفوتون

$$

$$\ updownarrow p_0 = \ updownarrow \ overline p_1 = 63 GeV / c \ uparrow \\ \ leftrightarrow p_0 = γ v \ overline {E_1} = (5/3) (4/5) 63 GeV / c = 84 GeV / c \ rightarrow \\ E = γ \ overline {E_0} = (5/3) 63 GeV = 105 GeV$$

بالنسبة للفوتون الثاني ، فإن الصيغ هي نفسها ، فقط مكونها الرأسي يتم توجيهه إلى أسفل. لاحظ أنه بالنسبة لكل من الفوتونات E = pc ، وفقًا لنظرية فيثاغورس للحجم p لكل نبضة ، وفقًا للرؤية الداخلية في الشكل. 10

$$

$$p_1 ^ 2 = (\ uparrow p_1) ^ 2 + (\ rightarrow p_1) ^ 2 \\ أو \\ (105 GeV / c) ^ 2 = (63 GeV / c) ^ 2 + (84 GeV / c) ^ 2$$

ومرة أخرى ، يلاحظ Kostya القيم الأخرى للطاقة والزخم ، مقارنةً بـ Petya و Masha. لكن بالنسبة لكوستيا ، لا تزال الطاقة والزخم محفوظة. يلاحظ Kostya أيضًا أن كتلة نظام يحتوي على فوتونين يتزامن مع كتلة Higgs. لماذا؟ إجمالي الجزء الرأسي من زخم النظام هو صفر ، ويتم تدميره بشكل متبادل. الجزء الأفقي من نبضة النظام هو 168 GeV / s. الطاقة الإجمالية للنظام 210 ج.ف. هذا هو ما لاحظته ماشا ، باستثناء أن زخمها في النظام قد ارتفع ، وليس إلى اليمين. لكن اتجاه النبض لا يؤثر على المعادلة رقم 1. فقط حجمه يلعب دورًا هناك. لذا ، مثل ماشا ، يرى كوستيا أن كتلة نظام البروتونين هي $$$126 GeV / c ^ 2$ يساوي كتلة جسيم هيجز الأولي.

الملخص

لذا نرى ما يلاحظه ثلاثة مراقبين مختلفين. ملاحظاتهم:

• تختلف حول طاقة هيجز والزخم ،
• تختلف من حيث الطاقة والزخم لكل من الفوتونات ،
• الاتفاق على الحفاظ على الطاقة والزخم أثناء الاضمحلال ،
• لذلك ، يتفقون على أن كتلة النظام محفوظة ،
• توافق على أن كتلة النظام هي 126 GeV / c ² ،
• علاوة على ذلك ، أن مجموع كتل أجسام النظام لا يتم الحفاظ عليه ، ولكنه ينخفض ​​من 126 GeV / c ² إلى صفر.

وهذه ليست مصادفة. عرف أينشتاين من التجارب السابقة أنه يتم الحفاظ على الطاقة والزخم ، لذلك بحث ووجد معادلات تحافظ على هذه الميزة للعالم. في هذه العملية أيضًا ، وجد أن كتلة النظام يجب أن تلبي المعادلة رقم 1.

المكافأة: كيف يتم استخدامها للبحث عن جسيم هيجز

العلماء:

• مراقبة تصادمات البروتون ، ونتيجة لذلك يولد فوتونان ؛
• حساب كتلة نظام الفوتونين (في المصطلحات الفنية ، وهذا ما يسمى الكتلة الثابتة لزوج من الفوتونات).

عندما ، نتيجة للتجربة ، يتحلل جسيم هيجز إلى فوتونين ، ثم بغض النظر عن اتجاه وسرعة تحرك الجسيم فيما يتعلق بالمختبر ، فإن نظام الفوتونين الذي يتحلل فيهما سيكون له دائمًا كتلة مساوية للكتلة جسيمات هيجز التي أنتجتها! لذلك ، على عكس العمليات العشوائية ، التي تؤدي إلى نظام من اثنين من الفوتونات ذات الكتلة العشوائية ، فإن جسيمات هيجز تولد دائمًا نظامًا من فوتونين من نفس الكتلة. لذلك ، إذا ظهرت جسيمات هيجز في نتائج التجربة ، وإذا كانت تتحلل أحيانًا إلى فوتونين ، فسوف نرى ذروة من تحلل هيجز ترتفع فوق خلفية ناعمة من العمليات العشوائية الأخرى. وهكذا حدث في التجربة على المصادم LHC!