كيفية صنع متعدد الوجوه المستحيلة: الرياضيات غير الواقعية في العالم الحقيقي

تعطينا الرياضيات صورة دقيقة للإجابات الدقيقة تقريبًا.

باستخدام ورق سميك وشريط شفاف ، يجمع Craig Kaplan جسمًا مستديرًا جميلًا يشبه إنشاء Buckminster Fuller أو نوع جديد عصري من كرة القدم. وتتكون من أربعة دوديكاجون عادية (12-gons مع نفس الزوايا والجوانب) و 12 decagons (10-sided polyhedra) مع 28 فتحات صغيرة في شكل مثلثات متساوية الأضلاع. هناك مشكلة واحدة فقط - هذا الرقم لا يمكن أن يوجد. لا تتطابق مجموعة المضلعات هذه مع القمم ، ولا يغلق الشكل.

يعمل نموذج كابلان فقط لأنه عندما تقوم بتجميعه من الورق ، يكون لديك القليل من حرية المناورة. يمكن أن تنحني الجوانب بشكل غير محسوس. يقول كابلان ، أخصائي تكنولوجيا المعلومات في جامعة واترلو في كندا: "إن هامش الخطأ الناشئ عن العمل في العالم الحقيقي بالورق يعني أن الأشياء التي لا يمكن أن تكون ممكنة بالفعل".



هذا مثال جديد من فئة من الأشياء الرياضية غير المتوقعة التي تعثر عليها عالم الرياضيات الأمريكي نورمان جونسون في الستينيات. عمل جونسون على الانتهاء من مشروع بدأ منذ أكثر من 2000 عام بواسطة أفلاطون - قام بإنشاء كتالوج من الأشكال الهندسية المثالية. من بين مجموعة لا حصر لها من الأشكال ثلاثية الأبعاد ، يمكن إنشاء خمسة فقط من نفس المضلعات العادية: رباعي السطوح ، ثماني السطوح ، سداسي السطوح ، icosahedron ، dodecahedron. إذا قمت بخلط مضلعات منتظمة مختلفة ، فيمكنك تكوين 13 شكلًا إضافيًا تلتقي فيها جميع المضلعات مع القمم - أجسام أرخميد - وكذلك المنشور (مضلعان متطابقان متصلان بمربعات) و "مضادات متضاربة" (مضلعان متطابقان متصلان بمثلثات متساوية الأضلاع).

في عام 1966 ، اكتشف جونسون ، أثناء عمله في جامعة ميشيغان ، 92 جثة أخرى تتكون فقط من مضلعات عادية ، والتي تسمى الآن [في الولايات المتحدة الأمريكية] أجسام جونسون . وهذا استنفد جميع الاحتمالات ، والتي أثبتت بعد ذلك بعدة سنوات من قبل عالم الرياضيات الروسي فيكتور أبراموفيتش زالجالر ، الذي عمل بعد ذلك في جامعة لينينغراد الحكومية. من المستحيل عمل أي شكل مغلق آخر من المضلعات العادية.

ولكن خلال جرد متعدد الوجوه ، لاحظ جونسون شيئًا غريبًا. وجد أشكاله ، يؤلف نماذجها من الكرتون والمطاط. نظرًا لوجود عدد قليل جدًا من الأشكال المتعددة الممكنة ، فقد توقع أن تظهر الأشكال الجديدة بسرعة إلى حد ما. إذا بدأت في رسم الوجوه معًا ، فيجب أن يتطابق الرقم بالضرورة. لكن هذا لم يحدث. يتذكر جونسون: "عند تجميع كومة من المضلعات ، لم يكن من الواضح دائمًا ما إذا كنت قد جمعت شكلاً صالحًا".

قد يبدو أن النموذج قد تم تجميعه ، ولكن "إذا أجريت الحسابات ، اتضح أن هذا ليس صحيحًا تمامًا" ، كما يقول. بعد الفحص الدقيق ، اتضح أن ما يبدو أنه مربع لم يكن مربعًا تمامًا ، أو أن الجوانب لم تكن مسطحة تمامًا. سيكون من الممكن تقليم الوجوه قليلاً ، وستكون مناسبة تمامًا ، ولكن بعد ذلك لن تكون مضلعات عادية.

عازمة على حساب جميع الأرقام المثالية ، لم يعلق جونسون أهمية على مثل هذه "الضربات الوثيقة". يقول: "لقد وضعتهم جانبًا ، وركزت على ما هو مقبول". لكن هذه الشخصيات المثالية تقريبًا لم تجذب انتباه كابلان ومحبي الرياضيات الآخرين فحسب ، بل أصبحت جزءًا من قسم أكبر من الرياضيات المثالية تقريبًا.

لا يوجد تعريف دقيق للنتيجة "الدقيقة تقريبًا". القواعد الصارمة لا تعمل في عالم متسامح. يسترشد كابلان الآن بطريقة تقريبية في البحث عن أرقام صحيحة تقريبًا: "خطأ رياضي حقيقي في شكل ما يمكن مقارنته بخطأ عملي ناتج عن العمل مع مواد من العالم الواقعي وأيد غير كاملة". وبعبارة أخرى ، إذا تمكنت من تجميع متعدد السطوح المستحيل - إذا كان قريبًا جدًا من الممكن أن تتمكن من تمريره على أنه حقيقي - فسيكون هذا الرقم دقيقًا تقريبًا. في الفروع الأخرى للرياضيات ، تكون النتائج الدقيقة تقريبًا قريبة جدًا من الحقيقة لدرجة أنها يمكن أن تخدعك أو تفاجئك - وهي نوع من النكتة الرياضية.

لا يمكن تسمية بعض هذه الشذوذ الرياضي بأي شيء أكثر من مجرد متعة ، في حين أن البعض الآخر يمكن أن يكون له معاني عميقة في الرياضيات والفيزياء.

تقع المشاكل القديمة المتمثلة في تربيع دائرة ومضاعفة مكعب في فئة الحلول الصحيحة تقريبًا. يبدو أنهم منفتحين بشكل مغري لإيجاد الحل الصحيح ، ولكن في النهاية يتبين أنهم مستحيلون - مثل الشكل الهندسي الذي يبدو مغلقًا ولكن ليس كذلك. بعض التصميمات التي رسمها ليوناردو دا فينشي وألبريشت دورر طويت الزوايا قليلاً ، مما أعطى خماسيًا منتظمًا تقريبًا على أنها حقيقية.



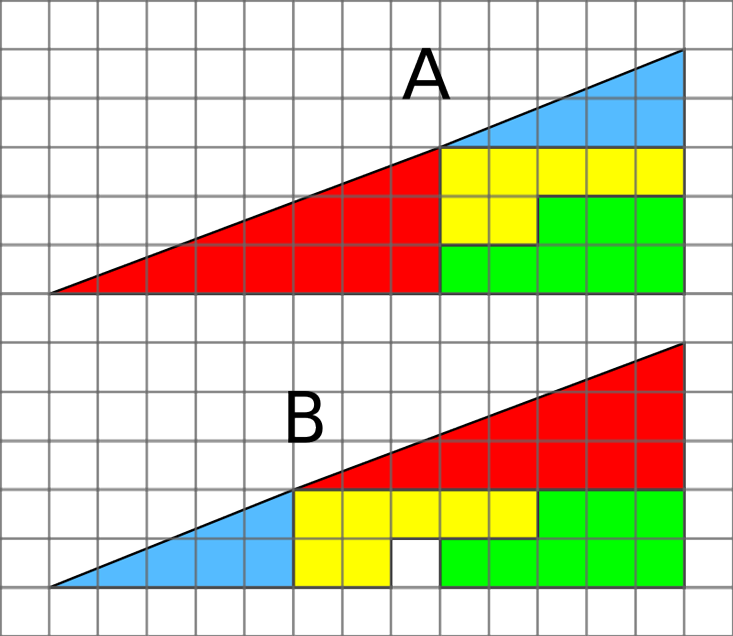
وهناك لغز مع مربع مفقود. في الشكل ، يتم قطع المثلث الأيمن إلى أربعة أجزاء. إذا قمت بإعادة ترتيبها ، تظهر فجوة فيها. من أين أتى؟ هذا هو أيضا القرار الصحيح تقريبا. لا شيء من المثلثات هو في الواقع مثلث. الوتر الخاص بهم ملتوي ، ويكاد يكون من المستحيل ملاحظة هذا هو السبب في أن الوهم مقنع للغاية.

تعد المطابقة الرقمية من أكثر القرارات المفيدة المفيدة في الحياة اليومية. ^2/12 يساوي 3/2 تقريبًا. لسبب مماثل ، يحتوي البيانو على 12 مفتاحًا في اوكتاف وفي قلب نظام الموسيقى الغربية المتوازن. هذا حل وسط بين أهم فترتين موسيقيتين: اوكتاف (التردد 2: 1) والخامس (التردد 3: 2). من الناحية العددية ، لا يمكن تقسيم أوكتاف بحيث تكون جميع الأخماس مثالية. ولكن يمكنك الاقتراب بما يكفي من ذلك عن طريق تقسيم الأوكتاف إلى 12 نصف نغمة ، ستعطيك سبعة منها تردد 1.498. بالنسبة لمعظم الناس ، هذا يكفي.

في بعض الأحيان تحدث الضربات الدقيقة تقريبًا في الرياضيات كما لو كانت تخدع نفسها. في حلقة عائلة سمبسون "Treehouse of Horror VI" ، لاحظ الجمهور المهتم بالرياضيات شيئًا غير عادي: المعادلة 1782 ¹² + 1841 ¹² = 1922 ¹² . للوهلة الأولى ، قد يبدو أن الكتاب دحضوا نظرية Fermat العظيمة ، وافترضوا أن المعادلة x ⁿ + y ⁿ = z ⁿ لا تحتوي على حلول صحيحة لـ n> 2. إذا أدخلت هذه الأرقام في حاسبة الجيب ، فستبدو النتيجة صحيحة. ولكن إذا أجريت حسابات بدقة غير متاحة لمعظم حاسبات الجيب ، فقد اتضح أن جذر الدرجة الثانية عشرة من الجانب الأيسر من المعادلة هو 1921999999955867 وليس 1922 ، ويمكن أن يكون Fermat هادئًا. زلة صغيرة بشكل مدهش - أقل من 10 مليون جزء.

لكن هذه الضربات الدقيقة تقريبًا ليست مجرد نكات. يقول جون بايز ، عالم الرياضيات في جامعة كاليفورنيا في ريفرسايد: "تلك التي تثير اهتمامي أكثر من غيرها هي حالات تلمح إلى وجود شيء أكثر أهمية". هذه هي حالة كمية تسمى أحيانًا ثابت رامانوجان . هذا الرقم e ^{π 3163} ، يساوي تقريبًا 262 537 412 640 768 743.9999999999999925 ، قريب بشكل مدهش من الكل. لا يمكننا أن نتوقع أن هذه الأرقام الثلاثة غير المنطقية - e و π و √163 - ستجمع بطريقة ما وتعطينا رقمًا منطقيًا ، ناهيك عن الرقم بالكامل. ولكن هناك سبب لتطابقهما بشكل جيد. يقول بايز: "إنها ليست مجرد مصادفة ليس لدينا أي فكرة عنها". "هذا هو مفتاح أعماق الرياضيات." التفسير الدقيق معقد إلى حد ما ، ولكن استنادًا إلى حقيقة أن 163 هي أكبر أرقام Hegner . العارضون المرتبطون بهذه الأرقام قريبون جدًا من الأعداد الصحيحة.

أو خذ اتصالًا رياضيًا يُعرف باسم "فرضية القمر الوحشي" (القمر الوحشي). القصة هي هذه: في عام 1978 ، جعل عالم الرياضيات جون ماكاي كيف تافهة ، ومثيرة للاهتمام ، الملاحظة: 196 884 = 196 883 + 1. الرقم الأول كان معامل متعدد الحدود مهم ، j- ثابت ، والثاني نشأ فيما يتعلق بكائن رياضي ضخم من نظرية المجموعة يسمى " الوحش ". كان الكثير من الناس يتجاهلون أكتافهم ويذهبون أبعد من ذلك ، لكن هذه الملاحظة كانت تهم العديد من علماء الرياضيات الذين قرروا دراستها عن قرب. ووجدوا صلة بين موضوعين يبدو أنهما غير مرتبطين: نظرية الأعداد وتماثل مجموعات مونستر. قد يكون لهذا الاتصال عواقب أوسع ، غير مفتوحة حتى الآن ، على مواضيع أخرى. يعتقد الفيزيائي إدوارد ويتن أن مجموعة مونستر يمكن أن ترتبط بالجاذبية الكمية وبنية الزمكان.

تظهر الضربات الرياضية شبه الصحيحة كل من المرح وقوة النهج البشري للرياضيات. توصل جونسون وكابلان وآخرون إلى اكتشافات من خلال التجربة والخطأ - ودرسوا المجال كعالم أحياء يتجول في الغابة بحثًا عن أنواع جديدة. ولكن في الرياضيات ، من الأسهل إجراء بحث منهجي. على سبيل المثال ، قام جيم ماكنيل ، المهتم بالرياضيات كهواية ويجمع مجموعة من الضربات الصحيحة تقريبًا على موقعه ، وقام روبرت ويب ، المبرمج ، بإنشاء برنامج لإنشاء ودراسة متعدد الوجوه.

ضربات دقيقة تقريبًا تعيش على الخط المموه بين الرياضيات المثالية والقاسية ومشاعرنا المتعاطفة والعملية. يستديرون منطق التقريب. عادة يعتبر العالم الحقيقي ظلًا غير كامل لعالم أفلاطون. يتم فقدان كمال الرياضيات الأساسية في تنفيذها. ولكن في حالة الضربات الدقيقة تقريبًا ، فإن العالم الحقيقي هو الظل المثالي للعالم الناقص. يقول كابلان إن التقريب هو "التقريب الخاطئ للإجابة الصحيحة" ، و "الضرب الدقيق تقريبًا هو تمثيل دقيق لإجابة دقيقة تقريبًا".

بهذه الطريقة ، تغير الإجابات الدقيقة تقريبًا العلاقة بين علماء الرياضيات والفيزيائيين الرياضيين مع الطبيعة. يقول كابلان: "أنا ممتن لعيوب العالم الحقيقي ، لأنها تسمح لي بتحقيق شبه مثالي من خلال العمل مع أشياء غير كاملة في الأساس". "إنهم يسمحون لي بالتغلب على قيود الرياضيات بفضل جمال الواقع المكسور."