نحن نفهم فيزياء الجسيمات: 1) كرة في الربيع ، النسخة النيوتونية

1. الكرة في الربيع ، نسخة نيوتن
2. كرة كمومية على زنبرك
3. الأمواج ، نظرة كلاسيكية
4. الموجات ، المعادلة الكلاسيكية للحركة
5. موجات الكم
6. الحقول
7. الجسيمات هي كمية
8. كيف تتفاعل الجسيمات مع الحقول

إن فهم أساسيات فيزياء الجسيمات بشكل عام - وهذا هو فهمنا الحالي لمعظم الظواهر الأولية للكون - ليس أمرًا صعبًا. سيكون من الأسهل بالنسبة لك إذا التحقت بمدرسة للفيزياء والرياضيات أو أكملت السنة الأولى من الكلية. ولكن إذا كنت تتعامل مع الجبر وعلم المثلثات و (ربما ، وليس بالضرورة) أساسيات التمايز والتكامل ، فيمكنك عندئذٍ فهم كيفية عمل الحقول وكيف تظهر الجسيمات. ما عليك سوى أن تأخذ كلمتي مرة واحدة ، فيما يتعلق بجانب واحد من ميكانيكا الكم. في هذه الحالة ، لن أقدم صيغًا رياضية ، ولكن ببساطة أريكم الإجابات الجاهزة. ولكن بعد قبول هذا الجانب ، سيكون كل شيء آخر واضحًا.


التين. 1

لفهم فيزياء الجسيمات ، من فيزياء المدرسة ، عليك أن تتذكر شيئًا واحدًا - كيف يعمل الربيع. في الواقع ، كل ما يرتد ، يهتز ، يرن ، يهز ، يتأرجح ذهابًا وإيابًا ، هو مثال على الربيع.

تخيل أننا وضعنا كرة في نهاية الربيع. إن حركات الربيع والمعادلات التي تصفه بسيطة. بادئ ذي بدء ، نتذكر أساسيات سلوك الربيع ، ثم ندرس سلوك الكرة - التذبذب. وأخيرًا ، بالنسبة للعقول الأكثر استفسارًا ، سننظر في المعادلات التي تؤدي إلى هذا النوع من الحركة.

مذبذب توافقي (يعرف أيضا باسم كرة في الربيع)

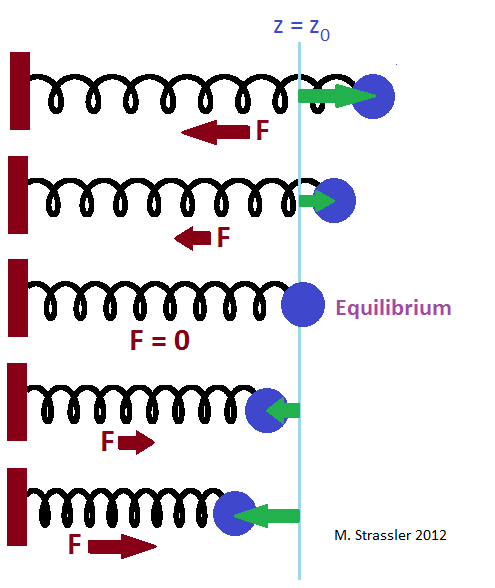
الكرة في الربيع لها وضع توازن ؛ إذا وضعت الكرة هناك وحررتها ، فلن يدفعها الربيع في أي اتجاه ، وستظل الكرة بلا حراك. هذا هو الخط الأزرق في الشكل. 1. إذا سحبت الكرة بعيدًا عن وضع التوازن (الأسهم الخضراء) ، فسوف يسحب الزنبرك الكرة مرة أخرى بالقوة F (الأسهم الحمراء). كلما قمت بسحب الكرة ، كلما سحبها الربيع بقوة (على الأقل حتى تكسر الربيع أو تكسره بالضغط).

حركة تتأرجح (القفز)

نسمي اتجاه حركة الكرة "الاتجاه z" ، ونحدد المحور z بحيث يتوافق z = z ₀ مع وضع التوازن للكرة في الربيع. لنفترض أننا سحب الكرة من هذا الموضع ، أمسكها حتى لا تتحرك ، إلى الموضع z = z ₀ + A ؛ ثم ، في وقت معين t = 0 ، نطلقه. ستبدأ الكرة في القفز هنا وهناك - انظر الشكل. 2. حجم القفزات - سعة التذبذبات - يساوي A. يمكن أن يكون كبيرًا أو صغيرًا بشكل تعسفي ؛ أنت فقط تختار مقدار سحب الكرة من وضع التوازن. لكنك لا تتحكم في عدد المرات التي تقفز فيها - وتواتر التذبذبات occur -. اتضح أنه هو نفسه ، بغض النظر عن قيمة A. يتم تحديده فقط من خلال خصائص الكرة والربيع ، وليس من خلال ما تفعله.

للأغراض العلمية ، من المهم للغاية وصف الملاحظات من خلال صيغة رياضية. موقع الكرة z هو دالة للوقت t ، كتبها من قبلنا z (t) ، يأخذ الشكل:

$$

$$z (t) = z_0 + A cos [2 \ pi \ nu t]$$

حيث ، كالمعتاد ، cos هو جيب التمام ، π هو الرقم pi من هندسة الدائرة ، z ₀ هو موضع التوازن للكرة ، و A و ν (nu) هي سعة وتردد التذبذبات. دالة جيب التمام متذبذبة ، لذلك تصف هذه الصيغة الحركات التذبذبية بسعة A وتردد ν. يتم عرض أمثلة على الحركة التذبذبية للكرة في نابض بقيم مختلفة للانحراف الأولي والسعة الكلية A في الشكل. 2 ، والذي يوضح أيضًا أنه بالنسبة لكرة معينة في الربيع ، لا يعتمد التردد frequency على السعة A.

طباعة دقيقة: السعة والتردد أكبر من الصفر. إذا كانت A سالبة ، فسيكون السعة –A. في الواقع ، السعة هي في الواقع | A | ، أي معامل الحجم.


التين. 2

ما هو مهم للغاية أن نتذكره حول اتساع وتواتر الكرة والربيع (في فيزياء ما قبل الكم الكلاسيكية):
• يمكن اختيار السعة A أي ؛
• التردد determined يتم تحديده بواسطة الكرة والربيع ، ومن أجل اختيار تردد مختلف ، عليك استبدال الزنبرك أو الكرة.

فترة كل تذبذب (المدة التي تستغرقها الكرة للتقدم للأمام والخلف مرة واحدة) ستسمى T ، وهذه الفترة هي ببساطة التردد المتبادل: T = 1 / ν. إذا كانت الفترة 5 ثوانٍ ، فسيكون التردد مرة واحدة كل خمس ثوانٍ ، أو 1/5 ثانية (والتي غالبًا ما تسمى 1/5 هرتز أو هرتز).

طباعة صغيرة أخرى: في أي نظام حقيقي للربيع والكرة التي ستواجهها في الحياة اليومية ، سيؤدي الاحتكاك إلى حقيقة أن A سينخفض ​​تدريجيًا ويصل في النهاية إلى الصفر عندما تتوقف الحركة. الصيغ التي تأخذ في الاعتبار الاحتكاك أثناء الحركة ليست أكثر تعقيدًا ، لكننا لن نحتاجها. لذلك ، أفترض دائمًا أن الاحتكاك صغير ، A ينخفض ​​ببطء شديد ، ويمكننا ببساطة استخدام الصيغ المبسطة التي تتجاهل الاحتكاك. ولكن من المهم أن تعرف: الاحتكاك يقلل A ، ولكن ، ما لم يكن قويًا للغاية ، لا يؤثر على ν و T! يبقى تردد التذبذب كما هو حتى مع انخفاض السعة. لذلك ، لا تتغير الملاحظة التي تنتجها سلسلة الغيتار بعد سحبها ، حتى عندما يتلاشى الصوت الناتج تدريجيًا.

شيء آخر: هناك صيغة جميلة للطاقة مخزنة في نوابض متذبذبة. يتناسب مع مربع السعة ومربع التردد:

$$

$$E = 2 \ pi ^ 2 \ nu ^ 2 A ^ 2 M$$

جزئيا ، هذه هي طاقة حركة الكرة (الحركية) ، وجزئيا ، طاقة التفاعل (المحتملة) المخزنة في الربيع ، وعندما تتأرجح الكرة ذهابا وإيابا ، فإن أجزاء هذه الطاقات في إجمالي الطاقة تتغير باستمرار. لكن الطاقة الكلية E تظل ثابتة.

طباعة صغيرة: لا تزال هناك طاقة كتلة الكرة ، Mc ² ، لكننا لا نتعقبها ، لأنها موجودة دائمًا ، يتحرك الربيع معها ، أم لا.

تنطبق نفس صيغة التذبذب على كل شيء تقريبًا يرتجف أو يقفز فقط إذا لم تكن هذه القفزات كبيرة جدًا. كرة تتدحرج على طول الجزء السفلي من الوعاء. سيارة تقفز على امتصاص الصدمات السيئة ؛ سلسلة تهتز من الكمان أو الغيتار ؛ شريط إكسيليفون بعد ضربه ؛ الخ.

معادلة الحركة الاهتزازية (قفز الرياضيات)

الآن دعونا نتذكر الصيغ الأساسية التي توضح لنا لماذا تتأرجح الكرة في الربيع.

كما ذكرنا في البداية (الشكل 1) ، فإن الكرة في الربيع لها وضع توازن ، والذي نسميه z = z ₀ . لنفترض في وقت ما (إما سحبنا الكرة ، أو ترددت) ، فهي في وضع مختلف ، z. إذا كانت z> z ₀ ، أي إذا كان الإزاحة من موضع التوازن z - z ₀ أكبر من الصفر ، فإن الزنبرك سيخلق قوة موجهة في الاتجاه السلبي z لسحب الكرة إلى نقطة التوازن. على العكس ، إذا كانت z <z ₀ ، أي أن الإزاحة من التوازن z - z ₀ سالبة ، فإن الربيع سيخلق قوة موجهة في الاتجاه الإيجابي z ، مرة أخرى لسحب الكرة إلى نقطة التوازن. وكلما كانت الكرة أبعد من وضع التوازن ، كلما سحب الربيع أقوى. ترتبط القوة F التي تم إنشاؤها بواسطة الربيع بإزاحة الكرة من التوازن بواسطة المعادلة

$$

$$F = - K (z - z_0)$$

حيث K هي قيمة موجبة ، اعتمادًا على نابض معين ، يسمى ثابت الربيع.

لاحظ سبب صحة هذه الصيغة:

• إذا كانت الكرة في وضع التوازن ، F = 0. فالنابض لا يخلق قوة ، وإذا لم تتحرك الكرة في وضع التوازن ، فسيبقى هناك.
• إذا كان الانحراف أكبر من الصفر ، تكون القوة سالبة.
• إذا كان الانحراف سالباً تكون القوة موجبة.
• كلما زاد الانحراف ، زادت القوة.

ثم ننتقل إلى قانون نيوتن الثاني للحركة ، الذي ينص على أنه تحت تأثير القوة F ، ستتحرك كرة الكتلة M مع التسارع a ، حيث F = M a. استبدل هذا في الصيغة واحصل على

$$

$$M a = - K (z - z_0)$$

أو

$$

$$a = - K / M (z - z_0)$$

هذه معادلة ضرورية تقريبًا بالنسبة لنا ، يمكننا من خلالها اشتقاق معادلة التذبذبات. نحتاج فقط إلى تذكر العلاقة بين a و z. لهذا ، من المهم أن نتذكر العلاقة بين a و speed v ، وبين v و z. هذه النسبة هي واحدة من تغييرين بمرور الوقت:
• السرعة هي تغيير في الموقع ، v = dz / dt
• التسارع هو تغيير في السرعة بمرور الوقت ، a = dv / dt

أضف واحصل على

$$

$$a = d (dz / dt) / dt = d ^ 2z / dt ^ 2$$

التسارع هو التغيير في وقت التغيير في الموقف بمرور الوقت.

يمكننا إعادة كتابة معادلة معادلة الحركة

$$

$$d ^ 2z / dt ^ 2 = - K / M (z - z_0) \ quad (*)$$

حيث z هي علامة قصيرة لـ z (t). والآن يمكننا التحقق من أن الحركة الاهتزازية z (t) = z ₀ + A cos [2 π ν t] ستكون حلاً لمعادلة الحركة هذه. نحتاج أولاً إلى حساب سرعة الجسيم كتغيير في موقعه في الوقت المناسب:

$$

$$d / dt (z_0 + A cos [2 \ pi \ nu t]) = - (2 \ pi \ nu) خطيئة [2 \ pi \ nu t]$$

(dz ₀ / dt = 0 ، حيث لا يتغير موضع التوازن z ₀ مع الوقت ، و d / dt (cos wt) = -w sin wt) ؛ ثم نحسب تسارع الجسيم كتغير في سرعته بمرور الوقت:

$$

$$d / dt [- (2 \ pi \ nu t)] = - (2 \ pi \ nu) ^ 2 A cos [2 \ pi \ nu t]$$

(منذ d / dt (sin wt) = w cos wt). نتيجة لذلك

$$

$$d ^ 2z / dt ^ 2 = - (2 \ pi \ nu) ^ 2 A cos [2 \ pi \ nu t] = - (2 \ pi \ nu) ^ 2 (z - z_0)$$

حيث استخدمت في الخطوة الأخيرة الصيغة z (t) = z ₀ + A cos [2 ν ν t] للحركة التذبذبية. المعادلة النهائية هي نفسها معادلة الحركة [ $$$d ^ 2z / dt ^ 2 = - K / M (z - z_0)$] ، بالنظر إلى أن (2 π ν) ² = K / M ، إذا كان تردد التذبذب

$$

$$ν = \ frac {\ sqrt {K / M}} {2 \ pi}$$

ووجدنا في الواقع أن معادلة الحركة تعني أن الربيع سيتذبذب مع التردد المشار إليه ، وأن هذا التردد لا يعتمد على A - إنه يعتمد فقط على خصائص الربيع (K) والكرة (M) - وأنه بغض النظر من الكمية A للمعادلة هناك حل. لذلك ، يمكننا اختيار أي A ، اعتمادًا على مدى سحب الكرة من وضع التوازن قبل تحريرها.

الرنين

الرنين هو أحد أهم الظواهر الطبيعية ، سواء في الحياة العادية ، حيث يلعب دورًا في العديد من جوانب التكنولوجيا والموسيقى ، وفي العمليات الأساسية للعالم المادي ، وخاصة في فيزياء الجسيمات.

أولاً ، تذكر كيف تعمل الأرجوحة. إن التأرجح ، مثل الكرة في الربيع ، أو أي بندول ، هو مذبذب - يتأرجح ذهابًا وإيابًا بتردد معين ، والذي لا يعتمد على سعة التأرجح. في حالة التأرجح ، تظل هذه العبارة صحيحة حتى تكون السعة كبيرة جدًا. ربما تعرف من التجربة أنه من أجل تأرجح طفل أعلى ، تحتاج إلى دفع التأرجح للأمام مرة واحدة لكل دورة بحيث يزداد اتساع الأرجوحة باستمرار. إذا قمت بدفع التأرجح للأمام عدة مرات لكل دورة ، أو مرة واحدة كل دورتين ونصف ، في بعض الأحيان ستزيد من سعة التأرجح ، وأحيانًا تقلله. من الواضح أن هناك شيئًا خاصًا حول محاذاة التردد الذي تدفع به التأرجح مع التردد الطبيعي للتأرجح نفسه.

وبالمثل ، إذا كان الطفل نفسه يعرف كيفية تأرجح الأرجوحة ، فهو يعرف أنه يحتاج إلى تأرجح ساقيه في نفس الوقت مع التردد الطبيعي للتأرجح من أجل زيادة سعة التأرجح. تأرجح بطريقة مختلفة ، ولن تنمو السعة.



يمكنك تتبع كيف يحدث هذا مع الكرة في الربيع. انظر إلى الصورة. على اليسار كرة تتأرجح وتتأرجح حول وضع التوازن. يتردد دون صدمات خارجية. يتأرجح مع التردد الطبيعي للنابض ν. التردد √ K / M ، حيث K هي قوة الربيع ، M هي كتلة الكرة.

على اليمين في الشكل. يمكنك أن ترى ما يحدث لكرة سوداء أخرى ، الكتلة تساوي الأولى ، في نفس الربيع ، والتي يتم دفعها بالقوة F (يظهر حجمها واتجاهها بواسطة السهم الأحمر) ، والتي تتأرجح بتردد frequency _F مختلف عن ν. كرة سوداء تتصرف مثل الأرجوحة التي نادرا ما تدفع. سوف يتحركون في نمط معقد ولن يتسلقوا عالياً. في الشكل. يمكن ملاحظة أن الكرة لا تتأرجح بسلاسة كبيرة ، وأن سعة التذبذبات صغيرة. يمكنك أن ترى كيف "يحاول" التأرجح بتردد طبيعي ، على الرغم من أن حركته العامة تتكرر بتردد ν _F.

ثم يوضح الشكل الحالة التي تتذبذب فيها القوة بتردد ν _F ، وهو أعلى بكثير من التردد ν. مرة أخرى ، يمكنك أن ترى كيف "يحاول" التذبذب بتردد طبيعي ، لكنه لا ينجح في القيام بذلك بسعة كبيرة ، حيث يمكن لقوة التأرجح السريع إما دفعها في الداخل أو ضد الحركة ، أو زيادة السعة أو خفضها .

وفي النهاية ، تظهر الحالة عندما تتأرجح القوة مع التردد الطبيعي للنابض ، ν _F = ν. تتفاعل الكرة بشكل مختلف تمامًا: يتزايد اتساع التذبذبات باستمرار ، وتتأرجح الكرة السوداء بسهولة وسلاسة مثل الكرة البيضاء على اليسار ، ولكن مع زيادة السعة. هذا رنين.

ونتيجة لذلك: إذا كانت ν _F تختلف عن ν - إذا كانت القوة لا تسمح للكرة بدخول الرنين - فسوف تتحرك ، ولكن على مضض ، وستكون حركتها مختلفة تمامًا عن الطبيعي ، من تذبذب بسيط بتردد ν. على العكس من ذلك ، إذا كان تردد القوة يتوافق مع المعدل الطبيعي - إذا أدخلت القوة الكرة في الرنين - فإن القوة تدفع الكرة بشكل أكثر كفاءة ، وتكون الحركة الناتجة أكثر إثارة للإعجاب. نحن نعرف ذلك بشكل حدسي. دفع الأرجوحة بتردد طبيعي ، الطفل (أو الوالد) يتأرجح الأرجوحة أعلى وأعلى.

من بين الجوانب المهمة للرنين في فيزياء الجسيمات حقيقة أنه في ظروف معينة يمكن أن تتولد الجسيمات بسبب آلية مشابهة جدًا: بعد اصطدام جسيمين ، يتم الحصول على قوة بنفس التردد بالضبط المطلوب لإنشاء ثالث.

المرة القادمة: كرة كمومية على زنبرك

هذا هو سلوك الكرة في الربيع في الفيزياء الكلاسيكية قبل الكم. تغير ميكانيكا الكم العديد من المفاهيم ، ولكن أهم شيء هو هذا: لا يزال بإمكاننا اختيار A ، ولكن لا يمكن أن يكون A بأي حجم. يمكن أن يستغرق فقط قيم معينة تتناسب مع الجذر التربيعي للأعداد الصحيحة.