نحن نفهم فيزياء الجسيمات: 3) الموجات ، الشكل الكلاسيكي

1. الكرة في الربيع ، نسخة نيوتن
2. كرة كمومية على زنبرك
3. الأمواج ، نظرة كلاسيكية
4. الموجات ، المعادلة الكلاسيكية للحركة
5. موجات الكم
6. الحقول
7. الجسيمات هي كمية
8. كيف تتفاعل الجسيمات مع الحقول

بعد التعامل مع معادلات التذبذبات - التي تصف تقريبًا كل ما يقفز ، يهتز ، يتدحرج ذهابًا وإيابًا ، مثل كرة في الربيع - يمكننا الانتقال إلى الظاهرة الطبيعية الشائعة ، الأمواج. الموجات في كل مكان: الصوت والضوء ، الزلازل ، التموجات على سطح البركة ، إلخ.


التين. 1

ولكن قبل ذلك ، أحذرك من أن مصطلح "الموجة" يمكن أن يكون مضللاً ، لأنه في الفيزياء لا يعني ذلك نفس اللغة الإنجليزية. في الفيزياء ، لا يعني هذا ما نسميه عادة موجة على حافة المحيط - قمة واحدة وأخرى مجوفة. في الفيزياء ، تعد الموجات سلسلة من الموجات ، والعديد من التلال والأحواض التي تتحرك معًا في نفس الاتجاه. في موجة من أبسط الأشكال ، تكون جميع التلال بنفس الارتفاع وتبعد مسافة واحدة عن بعضها البعض. سننظر فقط في مثل هذه الحالة.

الأمواج ظاهرة بارزة ، إذا فكرت في الأمر. تخيل أنك وصديقك قد سلكت حبلًا طويلًا وشدته بإحكام في الغرفة (الشكل 2). ثم تخيل أن صديقك تحدث إلى أعلى وأسفل عدة مرات مع أحد طرفي الحبل (أخضر). ستظهر موجة في نهاية الحبل وستمر عبر الغرفة حتى نهاية الحبل (أحمر).


التين. 2

هذا مذهل. أعني - إنه حقًا مذهل وقوي وحاسم لكل شيء في عالمنا ، بما في ذلك أنت شخصيًا. انظر ماذا حدث. لم يتم تحريك أي من الأشياء المادية من اليسار إلى اليمين - قبل أن يبدأ صديقك في تحريك نهاية الحبل ، تم تمديده عبر الغرفة ، وفي النهاية ، بعد توقف نهاية الحبل عن الاهتزاز واختفاء الموجة ، سيظل الحبل ممتدًا عبر الكل الغرفة ، كما كانت. ومع ذلك! انتقلت الطاقة والمعلومات حول الغرفة. تحمل الموجة الموجودة على الطريق الطاقة التي ينفقها صديقك على اهتزازات الحبل - وتحمل في شكلها معلومات حول عدد المرات وكيف سحبها بسرعة - إليك ، حيث تجعل اهتزاز يدك. وفي هذه الحالة ، سوف تصافح يدك عدة مرات وفي هذا التسلسل. واو! لم يتحرك شيء مادي واحد عبر الغرفة ، وانتقلت الطاقة والمعلومات.

أو انتظر. لكن ألا يجب أن نعتبر الموجة جسمًا ماديًا؟ ماديا مثل الحبل نفسه؟

تذكر هذا السؤال الأعمق ، ننتقل إلى عدد صغير من الصيغ الرياضية اللازمة لوصف مظهر وسلوك الموجة ، ثم نستخدم المزيد من الرياضيات لكتابة المعادلات التي تكون حلولها هي الموجات. هذا مشابه لما فعلناه من أجل كرة الربيع الكلاسيكية.

صيغة لموجة لا نهائية في وقت معين

هذه السلسلة من المقالات مباشرة بعد الكرة في الربيع تذهب إلى الأمواج لأن الموجة هي نوع من المذبذب المزدوج. يتقلب في الوقت والمكان. سنخصص الوقت بالحرف "t" ، والمسافة بالحرف "x".

انتبه إلى الشكل. 3. يصور موجة تمتد في كلا الاتجاهين على مسافة كبيرة ، حيث تناسب العديد من التلال والاكتئاب. هذا يختلف عن الموجة في الشكل. 2 ، التي لديها فقط عدد قليل من التلال والاكتئاب. لكن هذا الاختلاف غير ذي صلة - في الشكل. 2 احتجت إلى توضيح سبب عدم أهمية الشكل الموجي بالضبط ؛ الآن سنركز على الصيغة الرياضية للأمواج ، وسيكون من الأسهل القيام بذلك إذا كان للموجة عدد كبير من التلال والانخفاضات من نفس الحجم. أيضًا ، ستثبت هذه الحالة أنها مفيدة جدًا لفهم كيفية تأثير ميكانيكا الكم على سلوك الموجات.



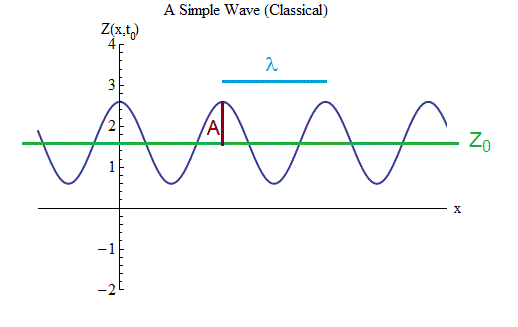
التين. 3

أولاً ، نحتاج إلى تحديد الترميز وكتابة صيغة تصف الحركة وشكل الموجة في الشكل. 3 ، كما فعلنا للكرة في الربيع.

يوضح الرسم البياني حجم الموجة Z كدالة للمسافة في فترة معينة من الزمن t = t ₀ - نسجل هذا على أنه Z (x، t ₀ ). عند تتبع الموجة في الفضاء ، نرى أنها تتأرجح للأمام وللخلف ، و Z تزداد وتنقص بشكل دوري. في أي لحظة من الزمن ، تتأرجح الموجة في الفضاء.

لاحظ أن Z لا يجب أن تكون مرتبطة بالمسافة الفعلية. يمكن أن يكون ارتفاع الحبل ، كما في الشكل. 2 ، أو يمكن أن يكون شيئًا مختلفًا تمامًا ، على سبيل المثال ، درجة حرارة الهواء عند نقطة معينة في المكان والزمان أو اتجاه ذرة مغناطيسية في مكان معين من المغناطيس. لكن س لا يزال يمثل المسافة المادية ، و t هو الوقت.

تحتوي لقطة هذه الموجة ، Z (x ، t ₀ ) على ثلاث خصائص مثيرة للاهتمام ، اثنان منها ينطبقان أيضًا على كرة في الربيع.

1. توجد قيمة توازن Z ₀ تقع في المنتصف بين أكبر قيمة Z على التلال وأصغر قيمة Z في الاكتئاب. معظم الوقت ندرس الموجات التي Z ₀ = 0 ، لأن القيمة Z ₀ غالبًا لا تهم - ولكن ليس دائمًا.
2. الموجة لها اتساع A ، وهي قيمة تتغير بها Z من قيمة التوازن إلى قمة كل سلسلة أو بنفس القيمة إلى أسفل كل منخفض.
3. للموجة طول - المسافة λ بين التلال المجاورة ، أو ، ما هو نفسه ، بين أحواض متجاورة ، أو ، وهي نفسها ، ضعف المسافة بين التلال المجاورة والحوض الصغير. يصف التذبذبات في الفضاء بنفس الطريقة التي تصف بها فترة (تساوي 1 / تردد) التذبذب في وقت كرة في الربيع.


التين. 4

ما يذكرنا بالشكل في الشكل. 3؟ يبدو وكأنه رسم بياني لوظيفة الجيب أو جيب التمام - انظر الشكل. 4 ، حيث يتم رسم cos (w) على w. Cos (w) هي دالة متذبذبة ، لها موقع توازن واضح عند الصفر ، وسعتها 1 ، وطول الموجة 2π. كيفية الانتقال من التين. 4 إلى صيغة الموجة في الشكل. 3؟ أولاً ، نقوم بضرب cos (w) في A ، بحيث يكون السعة مساوية لـ A. ثم نضيف Z ₀ إلى الصيغة بأكملها لتحويلها إلى قيمة التوازن المطلوبة (إذا كانت A = 0 ، فلا يوجد تذبذب ، وكل شيء يقع عند النقطة Z = Z ₀ ). وأخيرًا ، استبدل w بـ 2πx / λ ، نظرًا لأن cos (w) بها حواف عند w = 0 و w = 2 π ، وبالتالي ، عند cos (2πx / λ) ، ستكون الحواف عند x = 0 و x = λ. كل ذلك يعطينا

$$

$$Z (x، t_0) = Z_0 + A cos (2 \ pi x / \ lambda)$$

هذه هي تقريبًا نفس الصيغة التي وصفت حركة الكرة في الربيع في الوقت المناسب:

$$

$$z (t) = z_0 + A cos (2 \ pi \ nu t) = z_0 + A cos (2 \ pi t / T)$$

حيث ν هو تردد التذبذب ، و T = 1 / ν هي فترة التذبذب. انظر التشابه: تشير الفترة إلى الوقت حيث يشير الطول الموجي إلى الفضاء.

ملاحظة أخرى قبل أن نواصل. يمكنني أيضًا أن أكتب:

$$

$$Z (x، t_0) = Z_0 + A cos (- 2 \ pi x / \ lambda)$$

بما أن cos [w] = cos [-w]. إن حقيقة أنه يمكننا بسهولة استبدال السالب في صيغة الشكل الموجي ستكون مهمة لاحقًا.

صيغة لموجة لا نهاية لها في مكان معين

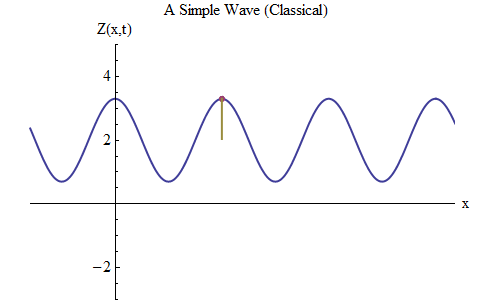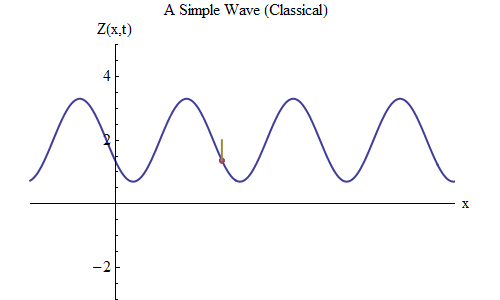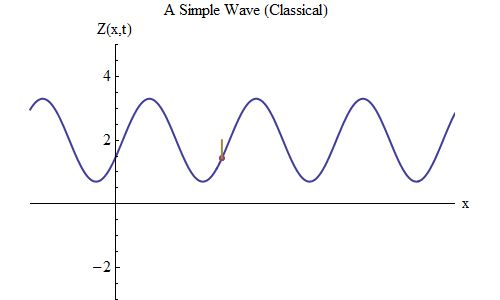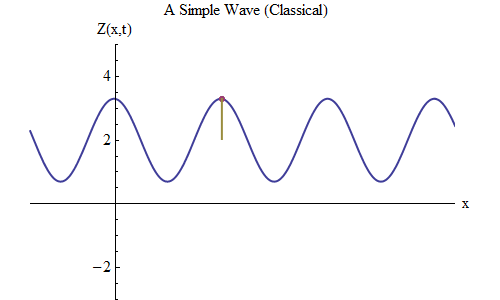التين. 5

الآن دعونا نطرح سؤالًا آخر: لنرى كيف تتغير الموجة في الوقت المناسب ، وتتبع نقطة معينة على الحبل ، ونرى كيف تتصرف وتتحرك. هذا مبين في الشكل. 5: هناك حددت نقطة معينة × ₀ ، والتي كانت في الوقت المناسب t ₀ على القمة. تتحرك الموجة إلى اليمين وتتبع حجم الموجة Z عند النقطة x ₀ ، متغيرة في الوقت: Z (x ₀ ، t). وسترى على الفور أن ارتفاع الموجة عند نقطة معينة يتصرف تمامًا مثل الكرة في الربيع! لذلك ، سيكون لها نفس الصيغة تمامًا مثل الكرة في الربيع ، كدالة للتردد ν ، أو الفترة T = 1 / ν ، حيث T هي الوقت بين اللحظة التي تكون فيها الموجة عند x ₀ على القمة ولحظة تقترب من القمة مرة أخرى في المرة القادمة.

$$

$$Z (x_0، t) = Z_0 + A cos (2 \ pi \ nu t) = Z_0 + A cos (2 \ pi t / T)$$

الصيغة الكاملة للموجة اللانهائية

الآن نحن بحاجة إلى صيغة لـ Z (x، t) تصف الموجة الموضحة في الشكل. 3 و 5 (أو أي نقطة مماثلة) في نقاط س في أي وقت ر. الجواب الصحيح هو:

$$

$$Z (x، t) = Z_0 + A cos (2 \ pi [\ nu t - x / \ lambda]) = Z_0 + A cos (2 \ pi [t / T - x / \ lambda])$$

يتضمن كلا الصيغتين ، لنقطة زمنية محددة ونقطة ثابتة في الفضاء.

لاحظ علامة الطرح أمام x. ذكرت أنه في صيغة Z (x، t ₀ ) يمكنك استبدال ناقص عند الرغبة. مع ناقص أمام x وزائد أمام t ، تصف الصيغة موجة تتحرك إلى اليمين ، كما هو الحال في الرسوم المتحركة. للتحقق من ذلك ، لاحظ أنه عند t / T - x / λ = 0 ، ستكون الموجة قمة لأن cos [0] = 1. عندما t = 0 ، عند النقطة x = 0 التلال. ولكن إذا تحركنا إلى الأمام قليلاً ، على سبيل المثال ، بواسطة T / 10 ، فستكون القمة عند النقطة x = λ / 10 ، على يمين المكان الذي كانت عليه عند t = 0 - وبالتالي فإن القمة (والموجة بأكملها) تتحرك إلى اليمين.

ما الذي سيتغير إذا وضعت زائدًا بدلاً من ناقص في صيغة Z (x، t)؟ ثم سيكون الشعار عند t / T + x / λ = 0 ، وفي هذه الحالة ، عند t = T / 10 ، سيكون الشعار عند x = -λ / 10 ، على يسار المكان الذي كان عليه عند t = 0 - مما يعني ، تتحرك الموجة الآن إلى اليسار (الشكل 6).


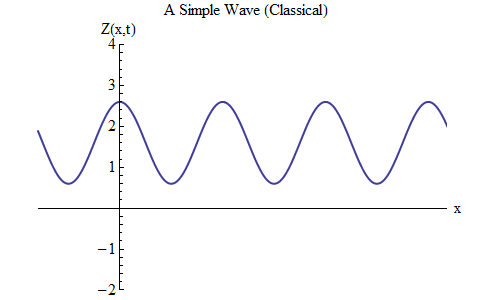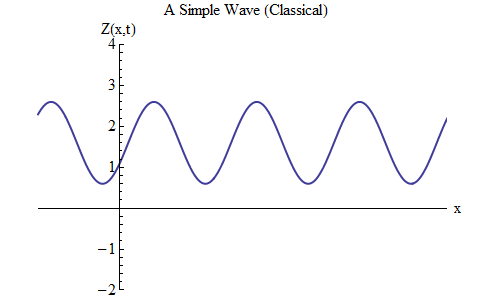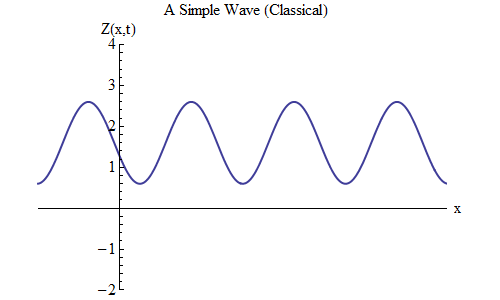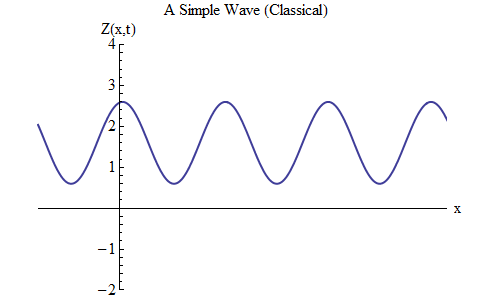التين. 6

يمكن أن تتحرك الموجات ، وهي وظائف x و t ، في أي اتجاه ، لذلك نحتاج فقط إلى اختيار الصيغة الصحيحة للموجة المحددة. بشكل عام ، عندما نعمل مع الموجات التي لا تتحرك فقط على طول البعد المكاني x ، ولكن على طول جميع الإحداثيات الثلاثة x و y و z ، يمكن أن تتحرك هذه الموجات في أي اتجاه ، وسنحتاج إلى اختيار الصيغة الصحيحة بناءً على الاتجاه حركة الموجة.

طباعة دقيقة: يمكننا وضع علامة الطرح أمام علامة t ، وليس قبل x. لكن + t ، + x هي نفس –t ، -x ، لأنها ستكون مساوية لضرب الصيغة بأكملها داخل جيب التمام ب -1 ، و cos [w] = cos [-w]. لذلك ، + t ، + x و -t ، -x تعطي موجة تتحرك إلى اليسار ، و + t ، -x و -t ، + x تعطي موجة تتحرك إلى اليمين.

معادلة الموجة

الآن ، كما في حالة الكرة في الربيع ، عندما وجدنا لأول مرة صيغة للحركة التذبذبية للكرة ، ثم نظرنا إلى معادلة الحركة ، التي كانت هذه الصيغة حلاً لها ، سنفعل الشيء نفسه هنا. وجدنا صيغة لشكل وحركة الموجة. أي معادلة للحركة بين الحلول لها مثل هذه الصيغة؟ نتعلم في المقالة القادمة.