نحن نفهم فيزياء الجسيمات: 6) المجالات

1. الكرة في الربيع ، نسخة نيوتن
2. كرة كمومية على زنبرك
3. الأمواج ، نظرة كلاسيكية
4. الموجات ، المعادلة الكلاسيكية للحركة
5. موجات الكم
6. الحقول
7. الجسيمات هي كمية
8. كيف تتفاعل الجسيمات مع الحقول

في الواقع ، لقد ذهبنا إلى الأراضي الميدانية منذ بعض الوقت ، لم أحذرك من ذلك - أردت التركيز على الموجات التي تنشأ في هذه المجالات. وصفنا كيف تتصرف الأمواج ، عبرنا عن شكلها واعتمادها على الوقت باستخدام الدالة Z (x، t). حسنًا ، Z (x، t) حقل. هذه هي وظيفة المكان والزمان مع معادلة الحركة التي تحدد سلوكها. تكون وظيفة الحركة المناسبة هي أنه إذا زادت Z أو نقصت عند نقطة معينة ، فإن Z ستنخفض أو تزيد في النقاط المجاورة بعد ذلك بقليل. تتيح هذه الميزة أن تكون الموجات من بين حلول المعادلة.

في هذه المقالة ، سنلقي نظرة على بعض الأمثلة على الحقول Z (x، t) التي تسمح معادلاتها بوجود موجات. سيكون التفسير المادي لهذه الحقول مختلفًا جدًا. يصفون الخصائص المختلفة للمواد المختلفة. لكن المعادلات التي يرضونها ، والموجات التي يظهرونها ، سترضي رياضيات متشابهة للغاية ، وسيتصرفون بشكل مماثل ، على الرغم من أصولهم المادية المختلفة. ستكون هذه نقطة مهمة للغاية في المستقبل.

ثم نفعل شيئًا جذريًا - ضع في اعتبارك الحقول في سياق النظرية النسبية الخاصة. كما أظهر أينشتاين ، إذا قمت بتصحيح المكان والزمان وأجبرتهم على القيادة ليس بالطريقة التي يتوقعها معظم الناس ، فستحصل على نوع جديد من الحقول - بحيث لا يكون تفسيره المادي خاصية لأي شيء آخر ، ولكنه كائن مادي مستقل.

المجالات العادية التي تصف الأشياء العادية

يمكن أن يمثل الحقل Z (x، t) العديد من الكميات المادية المختلفة. على سبيل المثال:
• امتد ارتفاع الحبل عبر الغرفة.
• ارتفاع الماء في النهر.
• كثافة البلورة أو الغاز.
• موضع الذرات في المغناطيس.
• سرعة الرياح.
• درجة الحرارة أو الكثافة أو ضغط الهواء.

في أي من هذه الحالات ، يوجد حقل Z (x، t): حقل ارتفاع ، مجال كثافة ، مجال اتجاه ، مجال الرياح ، ومجال درجة الحرارة. تخبرنا قيمته في شكل وظيفة للمكان والزمان بالارتفاع أو الكثافة أو الاتجاه أو سرعة الرياح أو درجة الحرارة لوسط معين - حبل أو نهر أو كريستال أو غاز أو مغناطيس أو هواء - في جميع الأماكن في أي وقت معين. تظهر معادلته للحركة كيف يمكن أن تتصرف Z (x، t) من حيث المبدأ. كما يوضح كيفية التنبؤ بسلوك Z (x، t) في المستقبل ، إذا علمنا تمامًا سلوكه في الحاضر والماضي.

في كل مثال ، يوجد مجال وبيئة ، ولا يجب الخلط بين الحقل والبيئة. يصف الحقل ببساطة ويميز إحدى الخصائص العديدة للبيئة المقابلة. يمكن أن تحتوي البيئات المختلفة تمامًا على مجالات سلوك متشابهة جدًا بموجات متشابهة جدًا - سنستمر في رؤيتها.

مرة أخرى سأوضح نقطة غالبا ما تسبب سوء الفهم. بشكل عام ، قد لا يكون للحقل أي علاقة بالمسافة المادية في الفضاء. نعم ، في المادتين 3 و 4 ، استخدمت مثال الثور على الحبل لتوضيح ما يمكن أن يكون Z (x، t) ، لأنه جميل وبديهي. كما أنني غالبًا ما أرسم الرسوم البيانية Z (x، t) للموجات. قد يعطيك هذا انطباعًا خاطئًا بأن Z (x، t) ترتبط دائمًا بالموجات التي تتسبب في تحرك جسم مادي (مثل الحبل) لمسافة Z في اتجاه متعامد مع المحور x. لكن الأمر ليس كذلك ، كما ستظهر لنا ثلاثة من أمثلةنا الأربعة.

حقل ارتفاع الحبل

أولاً ، ضع في اعتبارك مثالنا الأولي للموجات ، وهو حبل متذبذب. في هذه الحالة ، يكون دور Z (x، t) هو حقل الارتفاع الذي نسميه H (x، t). يخبرنا عن ارتفاع الحبل عند كل نقطة في الفضاء على المحور x الذي يمتد على طول الحبل في أي وقت. إذا كان الحبل عند ارتفاع التوازن H ₀ ، فإن H (x، t) = H ₀ . حقل الارتفاع ثابت في المكان والزمان. إذا تحركت موجة بسيطة من خلالها ، فسيتم وصف مجال الارتفاع من خلال صيغة الموجة الشهيرة من المقالات السابقة.

إذا كنا نعرف H (x، t) ، فإننا نعرف ارتفاع الحبل في جميع النقاط في المكان والزمان. إذا علمنا ما يفعله الحبل الآن وما كان يفعله مؤخرًا ، باستخدام معادلة الحركة يمكننا التنبؤ بما سيفعله في المستقبل. هذا يخبرنا القليل عن الحبل نفسه. حقل الارتفاع يعطينا فقط ما يوحي به اسمه: ارتفاع الحبل. الحبل هو وسط مادي يتم تمثيل ارتفاعه كمجال H (x، t) ؛ لا يخبرنا أي شيء عن لون الحبل ، سمكه ، توتره ، مادته ، إلخ.

في الشكل. 1 لقد صنعت لك رسمًا متحركًا لموجة في حقل ارتفاع ينتقل من اليسار إلى اليمين. قد يبدو أنني رسمت نفس الشيء مرتين ، أولاً باللون الأخضر ثم باللون البرتقالي. لكن هذا ليس نفس الشيء. المنحنى البرتقالي هو الحبل نفسه ، يتحرك في الفضاء المادي. المنحنى الأخضر هو رسم بياني يمثل ما يحدث مع H (x، t) ، بغض النظر عن معنى H (x ، t) (أي الارتفاع) ، أو أي نوع من البيئة. وفقط في هذه الحالة ، فإن الرسم البياني الأخضر يبدو تمامًا مثل ما يحدث في العالم المادي. ولكن في جميع الحالات الأخرى لن يكون الأمر كذلك.


التين. 1

حقل نزوح الشبكة

لنفترض أن لدينا وسيطًا يتكون من بلورة ذات ذرات موزعة بشكل موحد على مسافات متساوية من بعضها البعض. وجهتهم في صورة. 2 في بعد واحد - يمكنك تخيل مواقف مشابهة بثلاثة أبعاد ، ولكن في الوقت الحالي سيكون هذا تعقيدًا غير ضروري. قمت أيضًا بوضع علامة على كل ذرة 10 باللون الأحمر لتسهيل تتبع حركتها. كما أنني بالغت في المسافة بين الذرات - تخيل أنه بين كل نقطتين حمراء هناك عدة ملايين من الذرات وليس 10 ذرات.

ننظر إلى حقل الإزاحة D (x، t) ، الذي يخبرنا عن مقدار الوقت الذي انتقلت فيه الذرة ، التي تقع عادةً عند نقطة التوازن x ، من هذه النقطة في الشبكة. هذا يعني أنه في حالة الحالة الثابتة التي تبدأ منها الرسوم المتحركة ، يكون الحقل في كل مكان صفر ، D (x ، t) = 0 ، نظرًا لأن جميع الذرات في وضعها المعتاد. ثم ، في الرسوم المتحركة ، تبدأ الذرات الفردية تتأرجح ذهابًا وإيابًا ، وتنتقل حركتها بشكل عام في شكل موجة تتحرك من اليسار إلى اليمين. في الجزء العلوي من الشكل ، يوضح الرسم البياني لمجال إزاحة الشبكة D (x ، t) كيف يتصرف الحقل أثناء مرور الموجة. لاحظ أن الحقول في الشكل. يتصرف 1 و 2 بالمثل ، على الرغم من أن التفسير المادي للحقول مختلف تمامًا.


التين. 2

مجال التوجيه المغناطيسي

ما هو المغناطيس الدائم؟ يتكون من مجموعة من الذرات ، كل منها يعمل كمغناطيس صغير مع مجال مغناطيسي صغير ، وكلها محاذاة بحيث يخلقون معًا مجالًا مغناطيسيًا كبيرًا. يظهر المغناطيس في الشكل. 3 ، وفيه يتم توجيه كل ذرة إلى أعلى. في هذه الحالة ، يخبرنا حقل الاتجاه x (x، t) إلى أي مدى تنحرف الذرة عند النقطة x عن الرأسي. Θ ، باختصار ، ستكون الزاوية بين مغناطيس كل ذرة ورأسية. الرسوم المتحركة في الشكل. يظهر 3 موجة في مغناطيس تتأرجح فيها اتجاهات المغناطيس الذري يسارًا ويمينًا. يظهر رسم بياني x (x، t) فوق المغناطيس الأخضر ؛ ومرة أخرى يبدو هو نفسه تمامًا كما في الحالات السابقة.

مجال ضغط الهواء

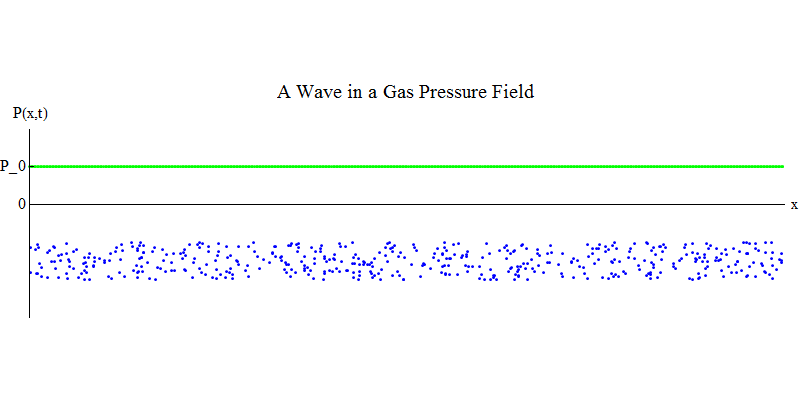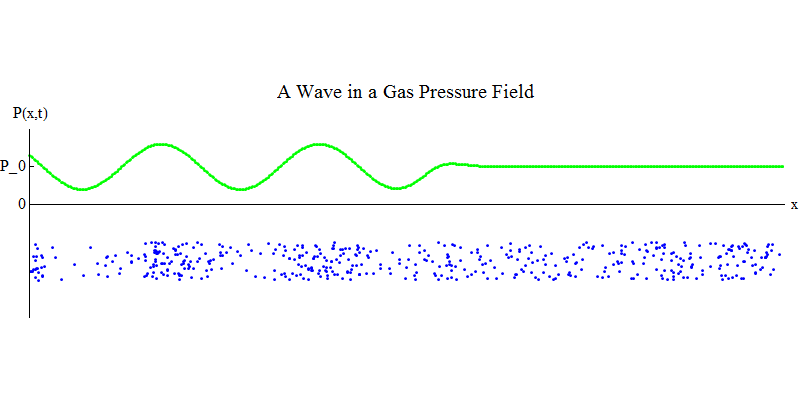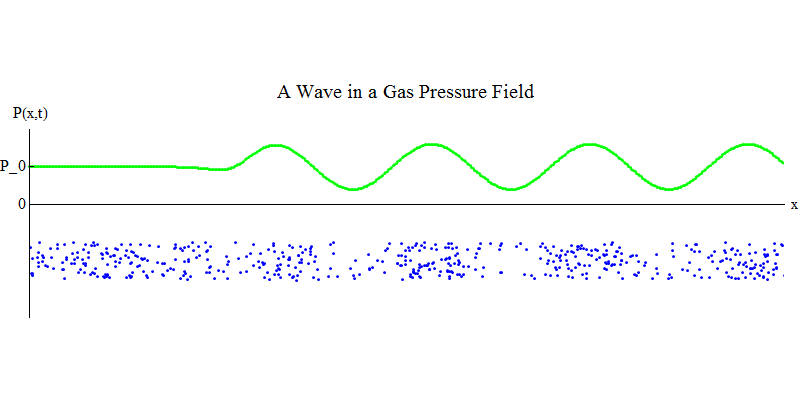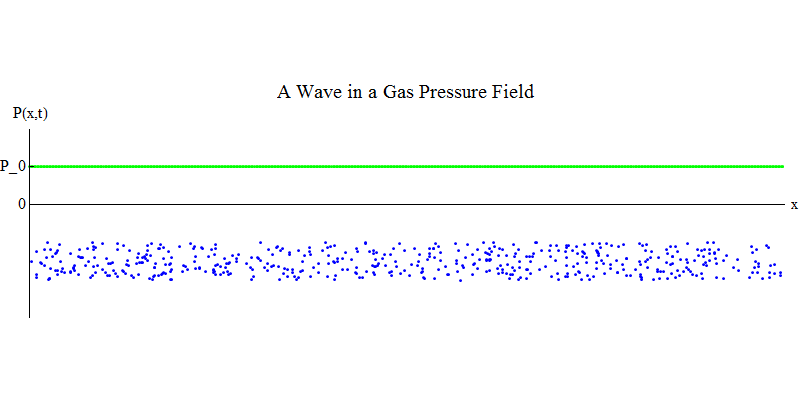
فكر في غاز جزيئي في أنبوب طويل. على طول الأنبوب سيكون البعد س. تتحرك جزيئات الغاز بشكل عشوائي تقريبًا ، وتتصادم مع جدران الأنبوب ومع بعضها البعض. في التوازن ، تكون الكثافة (عدد الجزيئات في حجم معين) والضغط P (x ، t) (القوة التي تعمل على سطح كرة صغيرة ظهرت عند النقطة x في الوقت t) ثابتة. لكن الموجات الصوتية التي تمر عبر الغاز سوف تتسبب في تأرجح الضغط والكثافة ، كما هو موضح في الشكل. 4. الكثافة والضغط يزدادان وينخفضان بشكل دوري. تتحرك الجزيئات للأمام والخلف ، على الرغم من أنها لا تتحرك في المتوسط ​​على الإطلاق ، ولكن في نفس الوقت تتحرك الموجة وطاقتها من اليسار إلى اليمين عبر الغاز. الرسم البياني P (x، t) يبدو مشابهًا جدًا للرسومات السابقة.

دروس مهمة

ماذا يمكننا أن نتعلم من أربعة أمثلة تظهر موجات الفئة 0؟ (معادلة الحركة لها كمية واحدة ، cw ، وجميع الموجات في المجال المقابل تتحرك بسرعة cw. الحقول المختلفة للفئة 0 سيكون لها قيم مختلفة من cw). يمكننا أن نكتشف أن نفس السلوك الميداني يمكن أن ينشأ من حقول مختلفة ماديًا موجودة في بيئات مختلفة جسديًا. على الرغم من أصلها المختلف ، تبدو الموجات في حقل الارتفاع ، في مجال إزاحة الشبكة ، في مجال التوجيه المغناطيسي وفي مجال ضغط الغاز متطابقة من وجهة نظر الحقول. إنها تستوفي نفس نوع معادلة الحركة ونفس العلاقة العددية للتردد وطول الموجة.

طباعة صغيرة: بشكل دقيق ، إذا قمت بإنشاء موجات بطول قصير بما فيه الكفاية ، فلا يزال بإمكانك التمييز بين سلوك الوسائط المختلفة. بمجرد أن تكون الأطوال الموجية مساوية للمسافة بين ذرات الحبل ، أو البلورة ، أو المغناطيس ، فإن معادلات الموجة التي ترضيها الموجات ستكون أكثر تعقيدًا من تلك التي كتبناها ، وستميز تفاصيلها الوسائط عن بعضها البعض. ولكن في التجارب العملية في كثير من الأحيان لا نقترب من ملاحظة مثل هذه التأثيرات.

والنتيجة هي أن دراسة الموجات وكميتها المتعلقة بالحقول لن تخبرك بالضرورة بما يخدم كوسيط ، أو ما هو التفسير المادي للحقل - أي خصائص الوسيط هي. وحتى إذا كنت تعرف بطريقة أو بأخرى أن هذا حقل من نوع معين - على سبيل المثال ، مجال ضغط - فعادة ما لا تتمكن من معرفة سلوكه عن الضغط الذي يمثله. كل ما يمكنك تعلمه من خلال دراسة الموجات هو ما إذا كان المجال ينتمي إلى الفئة 0 أو الفئة 1 ، وما هي قيمة cw ؛ أو اكتشف أن الحقل ينتمي إلى فئة أخرى.

في بعض الحالات ، هذا أمر سيئ للغاية. ينقل الحقل معلومات جزئية فقط حول البيئة. هذا في بعض الأحيان يكون مناسبًا جدًا ؛ المجال هو شيء أكثر تجريدية وعالمية من المادة المادية التي يصفها.

لذلك ، لا يحدد الحقل البيئة ، ولا يعتمد سلوكه غالبًا على تفاصيل وخصائص البيئة. بسبب ما يطرح السؤال.

هل يمكن أن يوجد مجال مادي - مع موجات تتكون من كمية تتحرك في الفضاء ونقل الطاقة - دون أي وسيلة تدعمه؟

حقل بلا وسيط؟

لا يمكنك سماع أغنية بدون مغني. لكن للأغنية نوع من الوجود المستقل. يبدو بشكل مختلف ، اعتمادًا على من يغنيها ، ولكن في نفس الوقت هناك شيء متأصل في الأغنية ، بعض الجودة المجردة ، وبفضل ذلك يمكن التعرف عليها دائمًا. هذا الكيان المجرد هو لحن الأغنية. يمكننا مناقشة ودراسة وتعلم اللحن وتسجيله بتسجيل موسيقي دون حتى سماعه من قبل المغني. يمكن للكثير منا حتى أن نفهم أنفسنا في رؤوسنا. بطريقة أو بأخرى ، لحن موجود حتى لو لم يقم أحد بأداء أغنية.

إذا كان كل الأمثلة التي قدمتها لي وفي جميع الأمثلة التي يمكنني تقديمها ، والتي ستكون واضحة لك بشكل بديهي ، يصف الحقل الخاصية من بينها ، فكيف يمكن أن يوجد حقل بدون بيئة؟ ولكن بطريقة ما ، تكون الحقول مستقلة عن بيئتها ، نظرًا لأن العديد من الحقول المختلفة يمكن أن تتصرف بنفس الطريقة ، على الرغم من أنها تصف العديد من الخصائص المختلفة لبيئات مختلفة تمامًا. لذلك ربما يكون من الممكن تجريد المجال من البيئة.

في الواقع ، هذا ليس ممكناً فقط ، يبدو أنه ضروري. على الأقل ، من الضروري إما أن لا يكون لديك وسيط ، أو أن تكون هناك بيئة لا يمكن إنشاؤها من مادة عادية ، والتي تختلف اختلافًا جوهريًا عن جميع الوسائط التي فحصناها - من حيث أنها تعمل بطريقة (وفقًا لجميع التجارب) أنها غير موجودة .

كان أحد العناصر الراديكالية العديدة لنظرية النسبية الخاصة لآينشتاين من عام 1905 هو فكرة أنه بالنسبة لموجات الضوء - لعقود تعتبر موجات في المجالات الكهربائية والمغناطيسية (الموجات الكهرومغناطيسية) ، وتتحرك بنفس السرعة في الفضاء الخالي - لا يوجد وسط. هناك حقول فقط.

كان الوسط الافتراضي يسمى "الأثير". جادل أينشتاين بأن مثل هذا الشيء غير موجود ، وكتب مجموعة من المعادلات التي لم تكن مطلوبة لها. ألاحظ أنه لا يزال هناك نقاش (غالبًا ما يكون أكثر فلسفية من المادية) حول ما إذا كنت بحاجة إلى تصور وجود بيئة غريبة مختلفة تمامًا عن المادة العادية أم لا. حتى الآن ، لا يوجد دليل يتطلب توافره.

كانت العناصر الرئيسية في نسخة النسبية لأينشتاين (على عكس إصدارات جاليليو ونيوتن) هي التالية:

• المكان والزمان ليسا كما تعتقد أنهما. يختلف المراقبون المختلفون الذين يتحركون بشكل موحد بالنسبة لبعضهم البعض في تقديراتهم لطول الأجسام والفترات الزمنية بين الأحداث (ويمكن قياس هذه الاختلافات بدقة).
• هناك حد للسرعة العالمية ، أي مراقب يقيس سرعة جسم ما فيما يتعلق به سيجد أن هذه السرعة أقل من أو تساوي s.
• في مثل هذا العالم ، يمكن أن توجد حقول معينة - "الحقول النسبية" - بدون وسيط ، وهي تلبي معادلات الحركة الخاصة. أبسط مجال نسبي يرضي معادلات الحركة للفئات 0 أو 1 ، مع سرعة الموجة cw المذكورة في معادلة الحركة مع القيمة c.

باختصار ، هناك مجالات نسبية من الفئة 0 تفي بالمعادلة

$$

$$Class 0: \؛ d ^ 2Z / dt ^ 2 - c ^ 2 d ^ 2Z / dx ^ 2 = 0$$

الضوء ، وجميع الموجات الكهرومغناطيسية ، هو المثال الأكثر شهرة ، ولكنه ليس فريدًا - لذلك ، غالبًا ما تسمى "ج" "سرعة الضوء". وهناك مجالات نسبية من الصنف الأول تفي بالمعادلة

$$

$$Class 1: \؛ d ^ 2Z / dt ^ 2 - c ^ 2 d ^ 2Z / dx ^ 2 = - (2 \ pi \ mu) ^ 2 (Z - Z_0)$$

سنرى أمثلةهم في المقالة التالية. لاحظ أن النسبية لا تفرض قيودًا على μ (باستثناء الحاجة ^إلى أن تكون μ ² موجبة) أو على Z ₀ . بالنسبة للحقول النسبية ، هناك معادلات أكثر تعقيدًا ، ولكن معظمها في وصف العمليات الفيزيائية البسيطة يتم اختزاله إلى أحد هذين.

المجالات النسبية حقيقية جسديًا ولها معنى مادي في الكون ، وهو:

• تحمل موجاتهم الطاقة والمعلومات من مكان إلى آخر.
• يمكن أن تؤثر الموجات في مجال واحد على مجال آخر وتغيير العمليات الفيزيائية التي ستحدث في غيابها.

ولكن ، على عكس الحقول ، التي ترد أمثلة عليها في هذه المقالة ، لا تصف الحقول النسبية خاصية أي وسيط مادي عادي ، يتكون من شيء يشبه المادة العادية ، وبقدر ما هو معروف تجريبيًا ، فإنها لا تصف خصائص أي شيء مهما حدث. هذه المجالات ، ربما ، على حد علمنا اليوم ، هي أحد العناصر الأساسية للكون.