نحن نفهم فيزياء الجسيمات: 7) الجسيمات هي كمية

1. الكرة في الربيع ، نسخة نيوتن
2. كرة كمومية على زنبرك
3. الأمواج ، نظرة كلاسيكية
4. الموجات ، المعادلة الكلاسيكية للحركة
5. موجات الكم
6. الحقول
7. الجسيمات هي كمية
8. كيف تتفاعل الجسيمات مع الحقول

وأخيرًا ، وصلنا إلى هدفنا: لفهم ما هي الأشياء التي نسميها "الجسيمات" ، في الواقع ، الإلكترونات والفوتونات والكوارك والغلوونات والنيوترينو. كل هذا ينطبق بالطبع على العلم الحديث. ومن الجدير بالذكر أنه في العلم لا توجد ضمانات بعدم تعميق الفهم الحالي.

وصفت المقالة السابقة ما هي الحقول - الأشياء التي لها معنى في أي وقت في الفضاء وفي أي لحظة من الزمن (وظائف المكان والزمان) ، وتفي بمعادلة الحركة ، وذات مغزى مادي من حيث أنها قادرة على نقل الطاقة من مكان إلى آخر والتأثير على العمليات الفيزيائية للكون.

علمنا أن معظم الحقول التي نعرفها تصف خاصية وسيطة ، مثل ارتفاع الحبل أو الضغط في الغاز. لكننا تعلمنا أيضًا أنه في نظرية أينشتاين عن النسبية ، هناك فئة خاصة من الحقول ، الحقول النسبية التي لا تتطلب وسيطًا. أو على الأقل إذا كان لديهم بيئة ، فهي غير عادية للغاية. لا يوجد شيء في معادلات المجال يتطلب وجود أي وسيط ولا يشير إلى خاصية هذه الوسيط الموصوفة بالمجالات النسبية.

حتى الآن ، سننظر في الحقول النسبية كأشياء مادية أولية للكون ، وليس كخصائص معينة لوسط غير معروف. ما إذا كان سيتم دعم وجهة النظر هذه بين الفيزيائيين - سيخبرنا الوقت.

نظرنا في فئتين من المجالات النسبية ، والآن سندرسها بمزيد من التفصيل. إما أنها تلبي معادلة الحركة من الفئة 0 ، حيث c _w = c (حيث c هي الحد الأقصى للسرعة العالمية ، غالبًا ما تسمى "سرعة الضوء").

$$

$$d ^ 2Z / dt ^ 2 - c ^ 2 d ^ 2Z / dx ^ 2 = 0$$

أو معادلات الحركة من الفئة 1 ، حيث cw = c

$$

$$d ^ 2Z / dt ^ 2 - c ^ 2 d ^ 2Z / dx ^ 2 = - (2 \ pi \ mu) ^ 2 (Z - Z_0)$$

في المقالة السابقة تبين أن μ هو الحد الأدنى لتردد الموجة في هذه المجالات. في هذه المقالة سنشير إليها في ν _دقيقة .

لماذا يُطلق على حد السرعة العالمي غالبًا سرعة الضوء؟ الموجات مع معادلة الفئة 0 تتحرك بسرعة c _w . الضوء (مصطلح عام يشير إلى الموجات الكهرومغناطيسية لأي تردد) يتحرك عبر الفضاء الخالي يرضي المعادلة النسبية للفئة 0 ، وبالتالي فإن موجات الضوء (وموجات أي مجالات نسبية ترضي المعادلة النسبية للفئة 0) تتحرك بسرعة c.

علاوة على ذلك ، رأينا في نفس المقالة أنه إذا كان المجال من الفئة 1 يحتوي على موجة ذات اتساع A وتردد ν وطول موجة state وحالة توازن Z ₀ ، فإن معادلة الحركة تتطلب أن يكون التردد وطول الموجة مرتبطين μ = ν _دقيقة تظهر في المعادلات بالصيغة

$$

$$\ nu ^ 2 = (c / \ lambda) ^ 2 + \ mu ^ 2 = (c / \ lambda) ^ 2 + \ nu_ {min} ^ 2$$

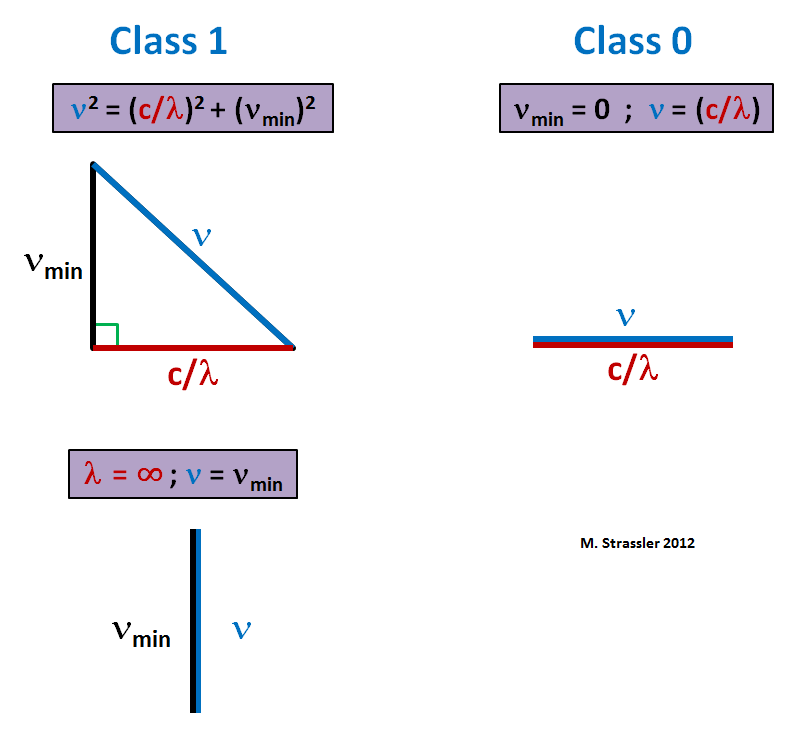
هذه صيغة فيثاغورس - يمكن تمثيلها ، إذا رغبت في ذلك ، في شكل مثلث ، كما في الشكل. 1. التردد الأدنى لأي موجة هو ν _min ، والتخصيص ν = ν _min (وبالتالي ، مثل λ → ∞) يتوافق مع ضغط المثلث إلى خط رأسي (الشكل 1 أدناه). يمكنك أيضًا الحصول على علاقة مماثلة من الفئة 0 بجعل μ = ν _دقيقة صفر. ثم يمكنك استخراج الجذر التربيعي ، والحصول على

$$

$$\ nu = c / \ lambda$$

هذا مثلث مضغوط إلى خط أفقي (الشكل 1 ، يمين). في هذه الحالة ، الحد الأدنى للتردد هو صفر. يمكن أن يتقلب الحقل بشكل تعسفي ببطء.


التين. 1

لا توجد قيود على أ. لكن هذا لأننا نتجاهل ميكانيكا الكم. حان الوقت لدراسة المجالات الكمية النسبية.

الحقول الكمومية النسبية

العالم الحقيقي ميكانيكي كمومي ، لذلك لا يمكن أن يكون السعة أي. يأخذ قيمًا منفصلة تتناسب مع الجذر التربيعي لـ n ، وهو عدد صحيح غير سالب يشير إلى عدد كميات الاهتزاز في الموجة. الطاقة المخزنة في الموجة

$$

$$E = (n + 1/2) h \ nu$$

حيث h هو ثابت بلانك ، يظهر بالضرورة حيث يهم ميكانيكا الكم. بمعنى آخر ، الطاقة المرتبطة بكل كم من التذبذبات تعتمد فقط على تردد تذبذب الموجة ، وهي تساوي

$$

$$E = h \ nu$$

تم اقتراح هذه النسبة لأول مرة ، على وجه التحديد لموجات الضوء ، بواسطة آينشتاين في عام 1905 ، في شرحه للتأثير الكهروضوئي.

ولكن دعونا نتذكر نسبة فيثاغورس للتكرار وطول الموجة. إذا ضربناها في h ² ، نحصل على ذلك في مجال الكم من الفئة 1

$$

$$E ^ 2 = (h \ nu) ^ 2 = (h c / \ lambda) ^ 2 + (h \ nu_ {min}) ^ 2 \ quad (*)$$

يبدو مألوفا. نحن نعلم بالفعل أن أي كائن في نظرية أينشتاين النسبية يجب أن يفي بالمعادلة التي تصف طاقتها وزخمها وكتلتها:

$$

$$E ^ 2 = (جهاز الكمبيوتر) ^ 2 + (mc ^ 2) ^ 2$$

علاقة أخرى فيثاغورس. الحد الأدنى من طاقة الجسم هو mc ² ، والذي يشبه البيان حول الحد الأدنى من التردد الذي يمكن أن تمتلكه موجة من الفئة 1 ، ν _min . قد نميل إلى افتراض أنه ، على الأرجح ، لمقدار مجال نسبي

$$

$$p c = h c / \ lambda \ quad (**)$$

$$

$$m c ^ 2 = h \ nu_ {min} \ quad (***)$$

ظهرت المعادلة الأولى لأول مرة في عمل لويس دي بروجلي في عام 1924 - بعد 20 عامًا تقريبًا من أينشتاين. لماذا استغرق وقتا طويلا؟ لا اعرف.


التين. 2

هل هذا منطقي؟ كما ذكرنا ، تتضمن الحقول النسبية من الفئة 0 أيضًا المجالات الكهربائية ، وموجاتها هي موجات كهرومغناطيسية ، أي الضوء. نسخة الصيغة (*) التي نحصل عليها للكمية من الفئة 0 هي نفسها لحقول الفئة 1 ، التي μ = ν _دقيقة تساوي صفر - أي m = 0. نستخرج الجذر التربيعي ونحصل على

$$

$$E = p c$$

أو معادلة أينشتاين للجسيمات عديمة الكتلة. وكمية الموجات الكهرومغناطيسية (بما في ذلك جميع أنواع الضوء: المرئية ، والأشعة فوق البنفسجية ، والأشعة تحت الحمراء ، والموجات الراديوية ، وإشعاع جاما ، وما إلى ذلك ، والتي تختلف في التردد فقط ، وبالتالي طاقة الكميات) ستكون جزيئات بلا كتلة - بمجرد تطبيقنا المشار إليه فوق معادلتين (**) و (***). هذه فوتونات.

من المعادلة (***) يمكننا في النهاية حساب كتلة الجسيم. كل جسيم له كتلة هو كم من مجال الفئة 1. الحد الأدنى لتردد مثل هذه الموجات ν _دقيقة . الطاقة الدنيا لكمية واحدة من هذه الموجة تساوي h ضرب التردد. وكتلة الجسيم هي ببساطة الحد الأدنى من الطاقة مقسومًا على c ² .

$$

$$m = h \ nu_ {min} / c ^ 2$$

إذا أردنا أن نفهم من أين تأتي كتلة الجسيمات ، فنحن بحاجة إلى فهم ما الذي يحدد ν _دقيقة ولماذا يوجد الحد الأدنى من التردد بشكل عام. بالنسبة لجسيمات مثل الإلكترونات والكواركات ، هذا غير واضح تمامًا ، ولكن من المعروف أن حقل هيجز يلعب دورًا مهمًا في ذلك.

نستنتج: جزيئات الطبيعة هي كميات من المجالات الكمية النسبية. الجسيمات عديمة الكتلة هي كمية من موجات المجال التي تلبي معادلة الفئة 0. تلك التي تمتلك كتلة تتوافق مع حقول معادلة من الفئة 1. هناك العديد من التفاصيل ، ولكن هذه الحقيقة هي واحدة من الخصائص الأساسية الأساسية لعالمنا.

هل تتصرف هذه الكميات حقًا مثل الجسيمات؟

نتخيل الجسيمات كجزيئات الغبار أو حبيبات الرمل. بهذا المعنى ، الكميات ليست جزيئات - هذه موجات لها الحد الأدنى من الطاقة والسعة لتردد معين. لكنهم يتصرفون إلى حد كبير مثل الجسيمات لدرجة أنه يمكن مسامحتنا لاستخدام كلمة "جسيم" في وصفهم. دعونا نرى لماذا.

إذا التقطت موجة في الماء وسمحت لها بالمرور عبر الحجارة التي تقع ضحلة تحت السطح ، فسوف يعبر جزء من الموجة خط الحجارة ، وسوف ينعكس جزء ، كما هو موضح في الشكل. 3. يعتمد أي جزء من الموجة سيعبر الخط على شكل الأحجار ، وقربها من السطح ، وما إلى ذلك. لكن خلاصة القول هي أن جزءًا من الموجة ينتقل عبر الأحجار ، وسينعكس الجزء. جزء من طاقة الأمواج سيذهب في نفس الاتجاه ، وجزء آخر يسير في الاتجاه المعاكس.


التين. 3

ولكن إذا قمت بإرسال فوتون واحد نحو الزجاج العاكس ، فسوف يمر هذا الفوتون من خلاله أو ينعكس (الشكل 4). بتعبير أدق ، إذا قمت بقياس سلوك الفوتون ، فستكتشف ما إذا كان ينعكس أو ينتقل. إذا لم تقيس ، فسيكون من المستحيل قول ما حدث. مرحبا بكم في مستنقع ميكانيكا الكم. الفوتون كم. لا يمكن تقسيم طاقته إلى الجزء الذي يمر عبر الزجاج والجزء المنعكس - لأنه بعد ذلك سيكون هناك أقل من كمية واحدة على كل جانب ، وهو ممنوع. (طباعة صغيرة: الزجاج لا يغير تردد الفوتون ، لذلك لا يمكن تقسيم الطاقة بين كميتين أو أكثر من الترددات المنخفضة). لذا فإن الفوتون ، على الرغم من كونه موجة ، يتصرف مثل الجسيمات في هذه الحالة. إما أنها تعكس الزجاج أم لا. لا تنعكس ميكانيكا الكم هذا الأمر سواء انعكست أم لا. إنه يعطي فقط احتمال التفكير. لكنها تتوقع أنه بغض النظر عما يحدث ، فإن الفوتون سيسافر كوحدة ويحافظ على هويته.


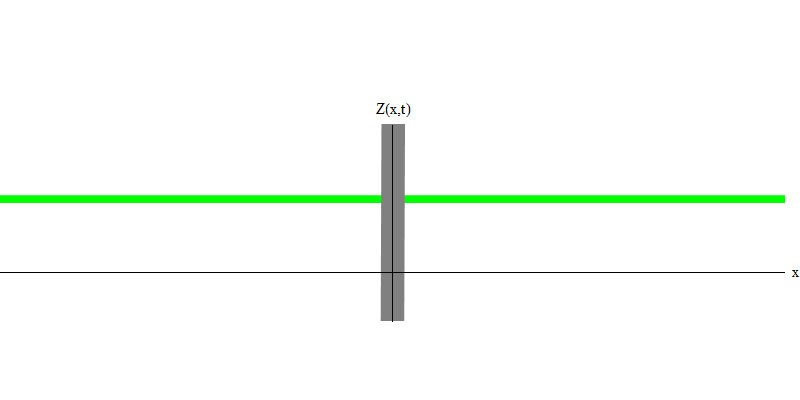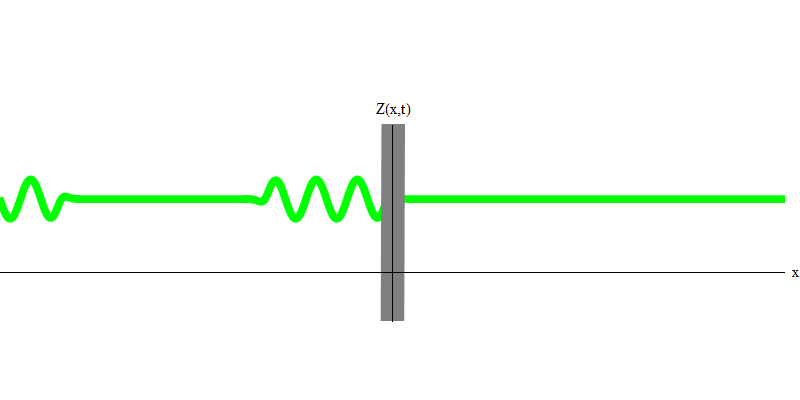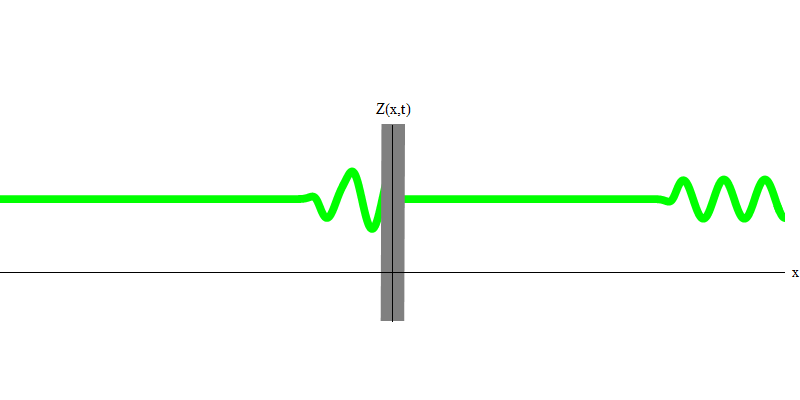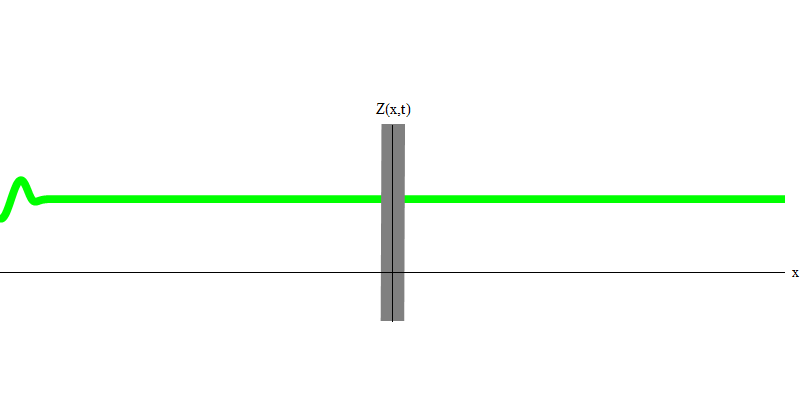التين. 4

وماذا سيحدث للفوتيين؟ هذا يعتمد. على سبيل المثال ، إذا انبعثت الفوتونات في أوقات مختلفة من أماكن مختلفة ، فسيشاهد المراقب كميتين ، مفصولة في الفضاء ، وربما تتحرك في اتجاهات مختلفة (الشكل 5). يمكن أن يكون لديهم ترددات مختلفة.


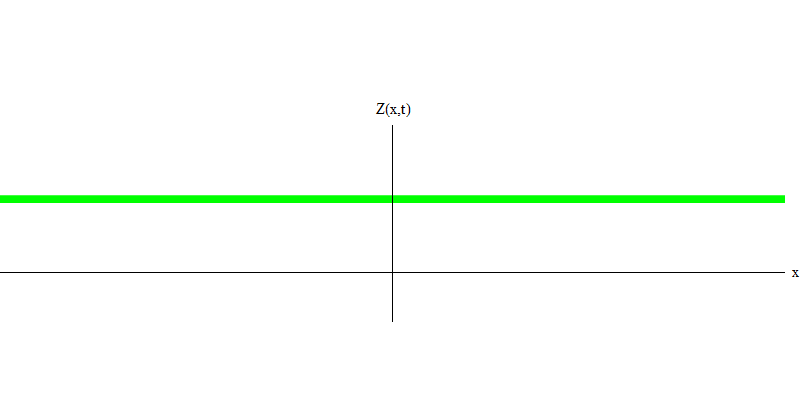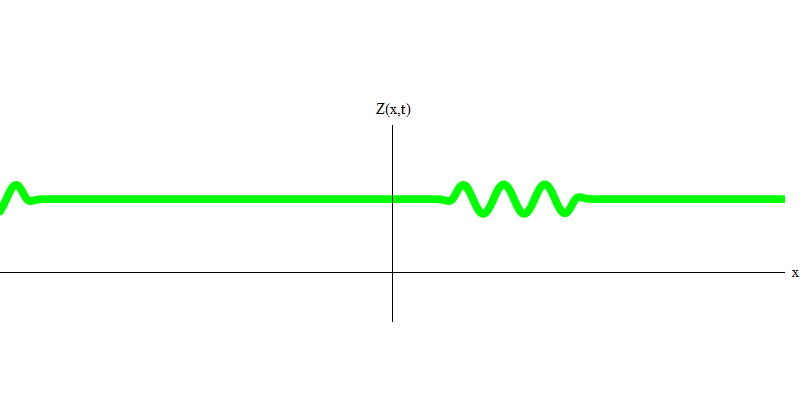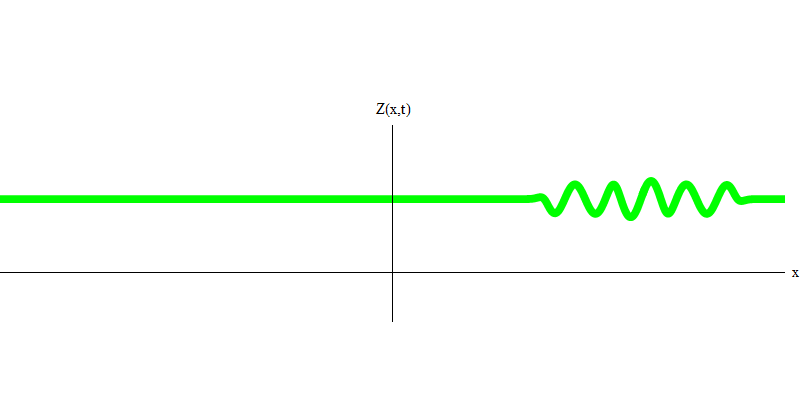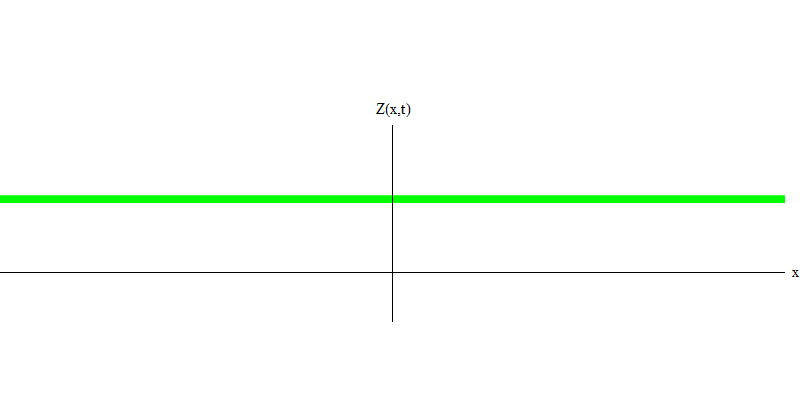التين. 5: الكميات المستقلة

في الحالة الخاصة ، عندما ينبعث فوتونان معًا وبشكل متزامن تمامًا (كما هو الحال في الليزر) ، يتصرفان كما هو موضح في الشكل. 6. إذا أرسلنا مزيجًا من فوتونين إلى الزجاج ، فلن يحدث اثنان ، ولكن يمكن أن يحدث ثلاثة أشياء. إما أن يمر كلا الفوتون من خلال الزجاج ، أو سينعكس كلاهما ، أو سيمر أحدهما ، والآخر سينعكس. سوف ينعكس 0 أو 1 أو 2 فوتون من الزجاج - لا توجد خيارات أخرى. بهذا المعنى ، تتصرف الكميات الخفيفة مرة أخرى مثل الجسيمات ، مثل الكرات الصغيرة - إذا رميت كرتين في شبكة بها ثقوب ، فستنعكس الكرات 0 أو 1 أو 2 من الشبكة ، وستمر الكرات 0 أو 1 أو 2 عبر الثقوب . لا توجد إمكانية لنعكس 1.538 هدفا من الشبكة.


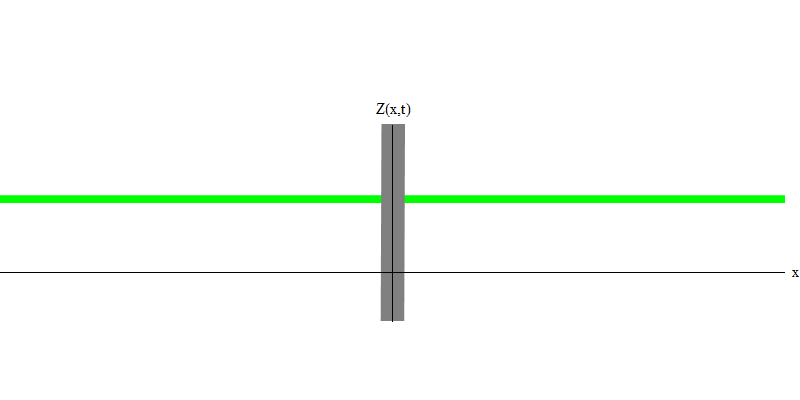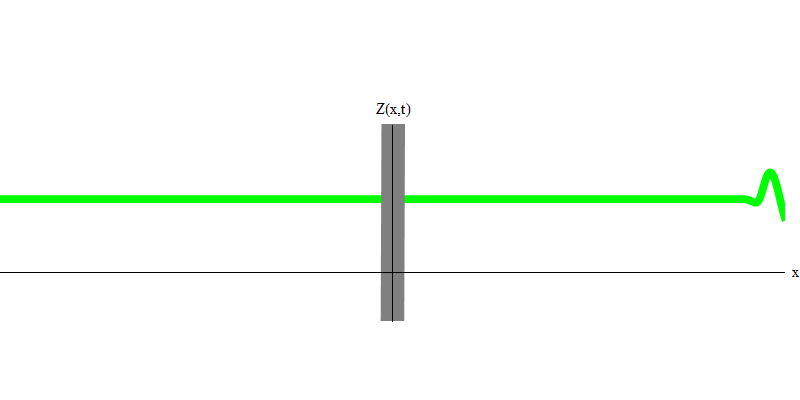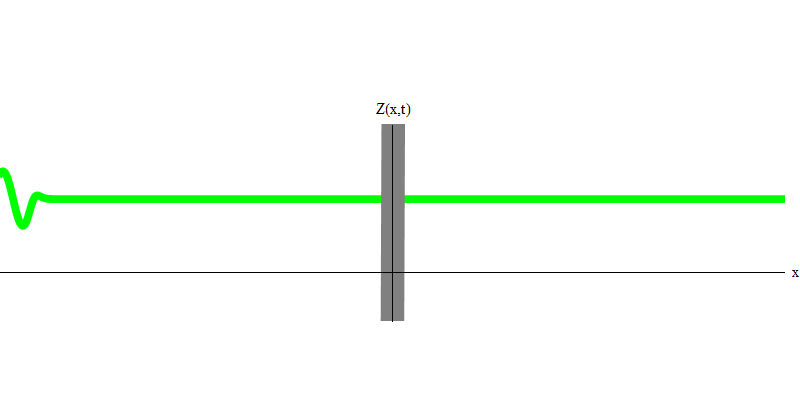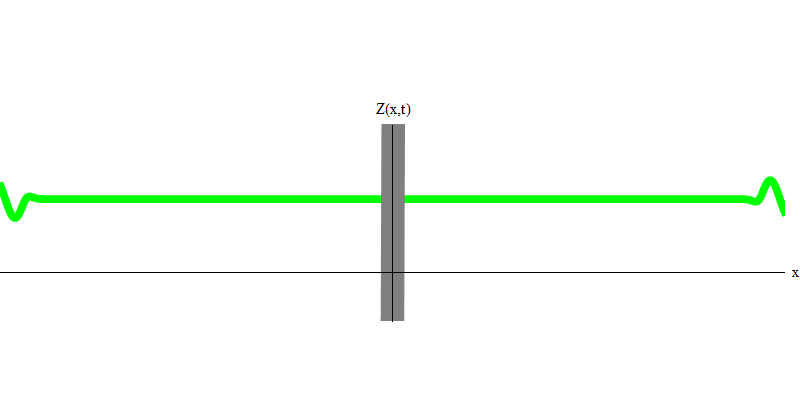التين. 6

لكن هذه الفوتونات ، بدون كتلة ، ملزمة بالتحرك بسرعة الضوء و E = p c. ماذا عن الجسيمات ذات الكتلة مثل الإلكترونات؟ الإلكترونات هي كمية من المجال الكهربائي ، ومثل الفوتونات ، يمكن أن تنبعث أو تمتص أو تنعكس أو تنتقل ككل. لديهم طاقة معينة وزخم ، $$$E ^ 2 = (كمبيوتر) ^ 2 + (m_e c ^ 2) ^ 2$حيث m _e هي كتلة الإلكترون. الفرق بين الإلكترونات والفوتونات هو أنها تتحرك أبطأ من الضوء ، وبالتالي يمكن أن تستريح. رسم توضيحي لمثل هذا الحدث (في ميكانيكا الكم ، بسبب مبدأ عدم اليقين ، لا شيء يمكن أن يكون ثابتًا حقًا) للإلكترون الثابت في الشكل. 7. هذه موجة من الحد الأدنى من الترددات التي يتم الحصول عليها عن طريق تعيين طول موجي بقيمة كبيرة للغاية ، لا نهائية تقريبًا. لذلك ، فإن الشكل الموجي المكاني في الشكل. لا تظهر أي تلافيف - إنها فقط تتقلب في الوقت المناسب.


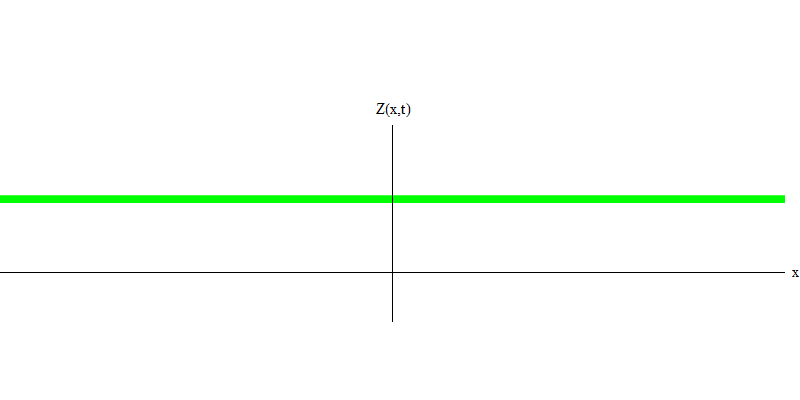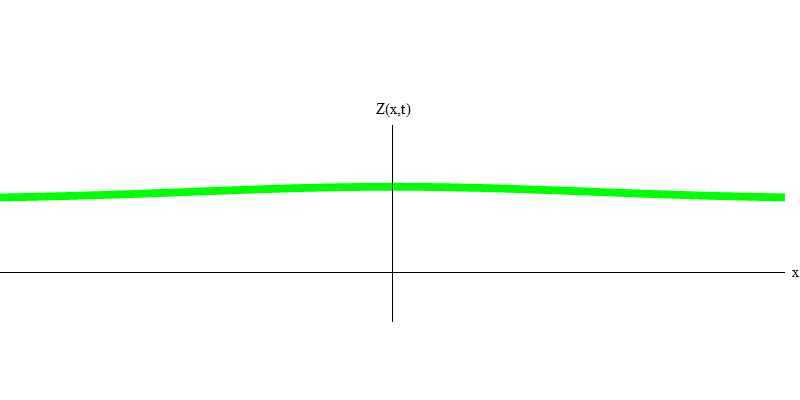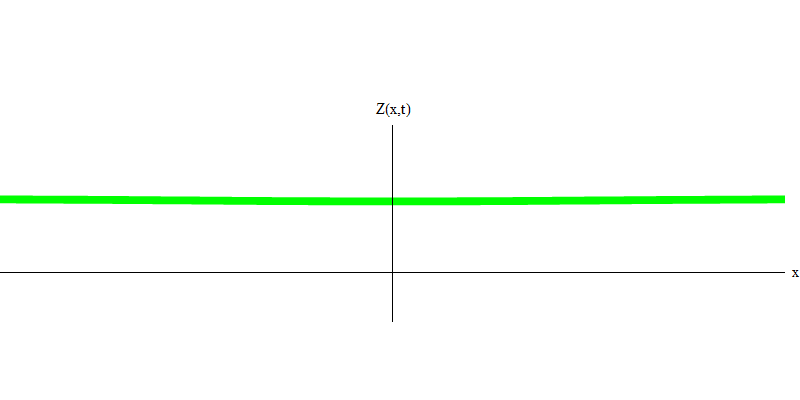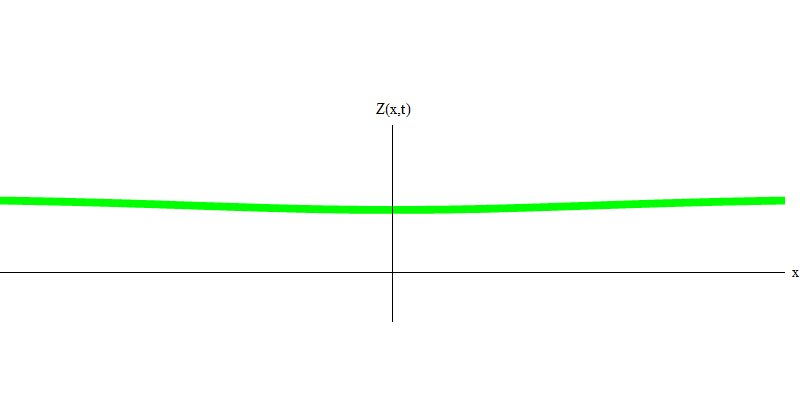التين. 7

لذا ، نعم ، في الواقع ، إن التصرف الكمي يشبه إلى حد كبير الجسيمات ، وبالتالي فإن تسمية الإلكترونات ، الكواركات ، النيوترينوات ، الفوتونات ، الجلوونات ، جزيئات W وجزيئات هيجز لن تكون خداعًا كارثيًا. لكن كلمة "كم" هي الأنسب لهذا - لأن هذه هي كميات بالضبط.

كيف تختلف الفرميونات والبوزونات عن بعضها البعض؟

• تنقسم جميع الجسيمات الأولية إلى الفرميونات والبوزونات.
• الفرميونات (بما في ذلك الإلكترونات والكواركات والنيوترينوات) تفي بمبدأ استبعاد باولي - لا يمكن لفرميونات من نفس النوع أن تفعل الشيء نفسه.
• البوزونات (بما في ذلك الفوتونات ، وجزيئات W و Z ، والغلوونات ، والجرافيتون ، وجسيمات هيجز) مختلفة: بوزونان أو أكثر من نفس النوع يمكن أن يفعلوا نفس الشيء.

هذا هو السبب في أنه يمكن تصنيع الليزر من الفوتونات - نظرًا لأنها بوزونات ، يمكن أن تكون في نفس الحالة وتولد شعاعًا قويًا من ضوء واحد. لكن لا يمكن تصنيع الليزر من الإلكترونات التي هي الفرميونات.

كيف يظهر هذا الاختلاف في لغة الرياضيات؟ اتضح أن الصيغ التي أحضرها مناسبة للبوزونات ، وبالنسبة للفرميونات ، يجب تغييرها - قليلاً ، ولكن مع عواقب كبيرة. بالنسبة للبوزونات ، سيكون لدينا:

$$

$$E = (n + 1/2) h \ nu ، \ quad حيث \؛ ن = 0 ، 1 ، 2 ، 3 ، 4 ، ...$$

مما يعني أن طاقة كل كم تساوي h ν. هذا يعني أن كمية البوزون يمكن أن تفعل الشيء نفسه. عندما تكون n أكبر من 1 ، ستتكون الموجة الموجودة في المجال البوزوني من عدة تذبذبات كمية وتتحرك معًا. لكن بالنسبة للفرميونات:

$$

$$E = (n - 1/2) h \ nu ، \ quad حيث \؛ ن = 0 \ ؛ أو \ ؛ 1 دولا$$

لا تزال طاقة الكم الواحد تساوي h so ، بحيث تظل المناقشة الكاملة للجسيمات وطاقاتها وزخمها وكتلها صالحة. لكن عدد الكميات في الموجة الإلكترونية يمكن أن يكون 0 أو 1. لا يمكن تنظيم عشرة إلكترونات ، على عكس عشرة فوتونات ، في موجة واحدة ذات سعة أكبر. لذلك ، لا توجد موجات فرميون تتكون من عدد كبير من الفرميونات ، تتأرجح وتتحرك معًا.