كتاب "كتاب صغير عن نظرية الأوتار الكبيرة"

غالبًا ما تسمى نظرية الأوتار "نظرية كل شيء" لأن غرضها هو وصف جميع القوى الأساسية للتفاعل في الكون ، بما في ذلك الجاذبية وميكانيكا الكم ونظرية النسبية. يقدم هذا المفهوم الثوري فهمًا جديدًا للمكان والزمان ؛ فهو يسعى إلى شرح اتصال الظواهر مثل الثقوب السوداء وبلازما الكوارك جلون والأبعاد الإضافية والتقلبات الكمية.

على الرغم من تعقيد الموضوع قيد النظر ، يقدم الأستاذ بجامعة برينستون ستيفين جابسر مقدمة قوية وممتعة ومسلية إلى هذا واحد من أكثر المجالات التي تمت مناقشتها في الفيزياء اليوم. مع الحد الأدنى من الرياضيات ، باستخدام تشابهات مثيرة للاهتمام ، يشرح المؤلف جوهر التناظر الفائق ، والثنائية ، وانحناء الزمكان بحيث يكون واضحًا لأي قارئ لديه مخزن للمعرفة بالمدرسة الثانوية.

على الرغم من أن أحكام نظرية الأوتار لم يتم إثباتها بشكل قاطع ، إلا أن تلك الأسرار التي تم الكشف عنها لنا بالفعل تسمح لنا بالإعجاب بالانسجام المتناغم للكون ومناقشة التطبيق العملي للاكتشافات المستقبلية في الفيزياء عالية الطاقة.

الجاذبية مقابل ميكانيكا الكم

تحولت ميكانيكا الكم والنسبية العامة - النظريتان الماديتان المنتصرتان اللتان نشأتا في بداية القرن العشرين - إلى عدم اتساق مع بعضهما البعض. تنشأ الصعوبة عند تطبيق طريقة تسمى إعادة التنسيق. سأتحدث عن إعادة التنسيق باستخدام مثال الفوتونات والجرافيتون ، الذي تحدثنا عنه بالفعل في الفصول السابقة. جوهر التناقض هو أن الفوتونات تقودنا إلى نظرية قابلة للتجديد (والتي تعني: "نظرية جيدة") ، بينما تؤدي الجاذبية إلى نظرية غير قابلة للتغيير ، وهذا يعني في الواقع أنه ليس لدينا نظرية عامة تصف الفوتونات والجرافيتون.

تتفاعل الفوتونات مع الشحنات الكهربائية ، لكنها نفسها محايدة كهربائيًا. على سبيل المثال ، إلكترون له شحنة كهربائية في ذرة هيدروجين ، يقفز من مستوى طاقة إلى آخر ، يصدر فوتونًا. هذا بالضبط ما أعنيه عندما أقول أن الفوتونات تتفاعل مع الشحنات. البيان بأن الفوتون نفسه ليس لديه شحنة كهربائية هو بمثابة البيان بأن الضوء لا يوصل الكهرباء. إذا لم يكن الأمر كذلك ، فستحصل على صدمة كهربائية في كل مرة ، وتمسك بشيء كان مستلقيا في ضوء الشمس لفترة طويلة بما فيه الكفاية. الفوتونات لا تتفاعل مع بعضها البعض. يتفاعلون فقط مع الشحنات الكهربائية.

لا تستجيب الجرافيتون للتهم ، بل للكتلة والطاقة والزخم. وبما أنهم ينقلون الطاقة ، فإنهم يتفاعلون أيضًا مع بعضهم البعض. قد يبدو أن هذا لا يمثل مشكلة معينة ، ولكن لهذا السبب بالتحديد نواجه صعوبات. تعلمنا ميكانيكا الكم أن الجاذبية تتصرف كموجات وكجسيمات. الجسيمات هي أشياء نقطة افتراضية. وسوف تجذبك نقطة الجاذبية الأقوى ، كلما اقتربت منه. يمكن وصف مجال الجاذبية بانبعاث جاذبية أخرى. سوف نطلق على تجربة الجرافيتون الأمومية ، والجاذبية التي ينبعث منها - ابنة. مجال الجاذبية بالقرب من الجاذبية الأم قوي جدًا. لذا ، تمتلك جاذبية ابنته طاقات هائلة وعزم. ويتبع هذا مباشرة من مبدأ عدم اليقين: يتم ملاحظة الجاذبية الأبوية على مسافة صغيرة جدًا fromx من الجاذبية الأصلية ، وبالتالي ، وفقًا لعلاقة عدم اليقين ، ×p × Δx ≥ h / 4π ، فإن عدم اليقين في الزخم ، Δp ، كبير جدًا. المشكلة هي أن الجرافيتونات حساسة أيضًا للزخم. الابراج الجاذبية نفسها سوف تنبعث الجاذبية. تتفرع العملية برمتها وتتشعب بسرعة لا تصدق: لا يمكنك أن تأخذ في الاعتبار جميع عواقب تفاعل جميع الجاذبية.

في الواقع ، يحدث شيء مماثل بالقرب من الإلكترون. إذا حاولت قياس المجال الكهربائي قريبًا جدًا من الإلكترون ، فاستحثه ليبعث فوتونًا بزخم كبير جدًا. يبدو هذا غير ضار لأن الفوتونات ، كما نعلم ، لا تنبعث منها فوتونات أخرى. تكمن المشكلة في أن الفوتون يمكن أن يولد زوجًا من الإلكترونات البوزيترونية ، والذي ينبعث بعد ذلك المزيد من الفوتونات التي تولد إلكترونات وبوزيترونات جديدة ... فوضى كاملة! الشيء الأكثر إثارة للدهشة هو أنه في حالة الإلكترونات والفوتونات ، يمكنك مع ذلك وصف كامل لكامل الجسيمات المتتالية من بعضها البعض. في بعض الأحيان يتحدثون عن الملابس أو "معاطف الفرو" من النسل الذي يلف فيه الإلكترون. يستخدم الفيزيائيون مصطلح "الجسيمات الافتراضية" لوصف النسل الإلكتروني. إعادة التطبيع هي طريقة رياضية تسمح لك بتتبع كل هذه الفوضى.


فكرة إعادة التطبيع هي أن الإلكترون "العاري" يفترض أن له شحنة لا متناهية وكتلة لا نهائية ، ولكن بمجرد أن "نلبس" إلكترونًا ، تكتسب شحنته وكتلته قيمًا محدودة.

مشكلة الجاذبية هي أننا لسنا قادرين على إعادة تنظيم سحابة الجاذبية الأرضية المحيطة بها. النظرية النسبية العامة - نظرية الجاذبية - غير قابلة للتكرار. قد تبدو هذه مشكلة فنية مربكة: هناك فرصة ضعيفة لأننا ببساطة ننظر إلى المشكلة من الجانب الخطأ. هناك أيضًا فرصة أضعف من أن تكون نظرية تسمى نظرية أقصى الجاذبية قابلة للتغيير. ومع ذلك ، أنا ومعظم منظري الأوتار مقتنعون بأن هناك صعوبات أساسية في الجمع بين ميكانيكا الكم والجاذبية.

الآن لنأخذ نظرية الأوتار. الافتراض الأولي الذي يقوم عليه هو أن الجسيمات ليست جزيئات نقطية. بدلاً من ذلك ، يتم تمثيل الجسيمات كأنماط اهتزازية لسلسلة. وفقًا للفكرة المقبولة عمومًا لنظرية الأوتار ، فإن السلاسل هي أشياء رقيقة بشكل لا نهائي ، ولكن لها طول محدود (من 10 إلى 34 مترًا) ، تتفاعل مع بعضها البعض بطريقة الجاذبية. توقف توقف! - أنت تحتج. "لكن في هذه الحالة ، ألن تقودنا المشاكل العامة مع سحابة الجسيمات الافتراضية - في هذه الحالة الأوتار الافتراضية - إلى نفس الاستحالة لتتبع عملية التفاعل بأكملها ، كما هو الحال مع الجاذبية؟" لا. حقيقة أن السلاسل النصية ليست كائنات نقطية تقتل المشكلة الموصوفة في البرعم. مصدر الصعوبة في حالة الجاذبية هو افتراض أنها ، وفقًا لمصطلح "الجسيم النقطي" ، صغيرة بشكل لا نهائي. يؤدي استبدال الجرافيت بخيوط اهتزازية إلى تنعيم "الزوايا الحادة" لتفاعلها مع بعضها البعض. "على الأصابع" يمكن تفسير ذلك على النحو التالي: عندما يؤدي الجرافيتون إلى جاذبية افتراضية أخرى ، يمكنك تحديد المكان والزمان اللذين حدث فيهما ذلك بدقة. ولكن عندما تتفرع الخيوط ، تبدو وكأنها فرع من أنبوب ماء.


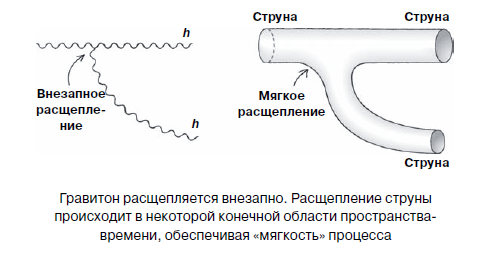
عند نقطة التفرع لا توجد نقطة يحدث فيها كسر ، يبدو الشكل على شكل حرف Y الذي يوضح هذه العملية كقطعة أنابيب ناعمة ومستمرة ، فقط من شكل غير عادي. كل هذا يؤدي إلى حقيقة أن تقسيم الخيط هو عملية "لطيفة" أكثر من تقسيم الجسيم. يقول الفيزيائيون أن الخيوط تتفاعل مع الطبيعة "بهدوء" ، بينما تتفاعل الجسيمات مع الطبيعة "بقوة". هذه هي النعومة التي توفر أفضل سلوك لنظرية الأوتار من النظرية النسبية العامة ، فيما يتعلق بتطبيق الوصف الميكانيكي الكمومي.

سلاسل في الزمكان

تذكر باختصار ما كنا نتحدث عنه عن اهتزازات سلسلة البيانو. إذا سحبت الخيط بإحكام بين شدتين وضربته بمطرقة ، فسوف يهتز بتردد معين. التردد هو عدد التذبذبات في الثانية. بالإضافة إلى التردد الرئيسي ، تهتز سلسلة البيانو أيضًا على النغمات ، وهي اهتزازات للترددات الأعلى التي تمنح صوت البيانو لونًا مميزًا. لقد استشهدت بهذا التشبيه عند وصف سلوك الإلكترون في ذرة الهيدروجين: كما أن لديها وضع اهتزاز أساسي يتوافق مع حالة الأرض مع الحد الأدنى من الطاقة ، وأنماط إضافية تتوافق مع مستويات طاقة أعلى.

قد لا يرضيك التشبيه الموصوف تمامًا: "حسنًا ، ما علاقة الإلكترون في ذرة الهيدروجين بالموجة الواقفة على وتر البيانو؟" - تسأل. معظمها أقرب إلى القياس مع دوران كوكب صغير لا نهائي في مدار حول الشمس الصغيرة - النواة الذرية ، أليس كذلك؟ هل هذا القياس جيد؟ نعم ولا. تدعي ميكانيكا الكم أن فكرة الإلكترون كجسيم وفكرة الإلكترون كموجة متشابكة للغاية لدرجة أن الحركة الكمومية الميكانيكية لجسيم إلكترون حول بروتون يمكن وصفها حقًا بأنها موجة قائمة.

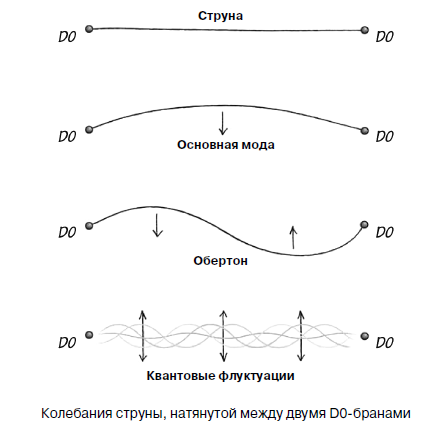
إن مقارنة سلسلة بيانو مع الأوتار التي تظهر في نظرية الأوتار هي في الواقع طريقة صحيحة للغاية. لتجنب الخلط بين أنواع السلاسل المختلفة ، سأسمي تلك السلاسل التي تتعامل معها نظرية الأوتار مع "سلاسل النسبية". هذا المصطلح له معنى تعليمي عميق للغاية ، لأن نظرية الأوتار تشمل نظرية النسبية ، خاصة وعامة. الآن أريد أن أتحدث عن بناء واحد لنظرية الأوتار التي تشبه إلى حد كبير سلسلة البيانو كما يمكن أن تكون السلسلة مثل سلسلة. يمكن أن تنتهي الأوتار النسبية بأشياء تسمى D-branes. إذا قمنا بحذف التأثيرات المرتبطة بتفاعل السلاسل ، فيمكن اعتبار D-branes ثقيلة بشكل لا نهائي. سيتم مناقشة التفاصيل حول D-branes في الفصل التالي ، والآن سأقوم فقط باستطراد صغير ، إذا جاز التعبير ، كـ "عكاز". أبسط D-brane يسمى D0-brane (وضوحا "de-zero brane"). هذا جسيم نقطي. يمكنني بالفعل سماع سخط بعض القراء حول العودة إلى الجسيمات النقطية: "ألم يذكر المؤلف مؤخرًا أن نظرية الأوتار تهدف إلى التخلص من الجسيمات النقطية؟" حسنًا ، نعم ، كان ذلك حتى منتصف التسعينات ، ثم عادت الجسيمات النقطية مرة أخرى إلى نظرية الأوتار ، وليس وحدها ، ولكنها أدت إلى حديقة حيوانات كاملة من حيوانات مجهولة. لكنني أتقدم على نفسي. كل ما أريد القيام به هو إعطاء النظير النظري للأوتار لأوتاد البيانو التي تمسك بالسلسلة في حالة متوترة - و D0-branes مناسبة جدًا في هذا الدور لدرجة أنني لا أستطيع مقاومة إخبارهم عنها. باختصار ، نسحب السلسلة النسبية بين اثنين من النخالة D0 ، مثل سلسلة البيانو بين اثنين من الأوتاد. لا ترتبط أغشية D0 بأي شيء ، لكنها تظل بلا حراك لأن لها كتلة لا حصر لها. مضحك ، أليس كذلك؟ حسنًا. حول D0-branes - في الفصل التالي ، والآن - فقط حول سلسلة ممتدة.

يتوافق أدنى مستوى للطاقة في السلسلة الممتدة مع عدم وجود اهتزازات. حسنًا ... غائب تقريبًا ، لأن التذبذبات الكمومية الصغيرة موجودة دائمًا ، وهذه الحقيقة مهمة. من الأصح أن نتخيل انخفاض مستوى الطاقة على أنه يمتلك طاقة اهتزازية صغيرة في إطار ما تسمح به ميكانيكا الكم. تتوافق المستويات المتحمسة لسلسلة نسبية مع اهتزازاتها إما عند التردد الأساسي أو نغمات التردد الأساسي ، ويمكنها أيضًا الاهتزاز عند عدة ترددات في وقت واحد ، تمامًا مثل سلسلة البيانو. ولكن ، تمامًا مثل الإلكترون الموجود في ذرة الهيدروجين ، لا يمكن أن تهتز السلسلة النسبية بتردد تعسفي. يمكن للإلكترون تحديد مستويات الطاقة من مجموعة منفصلة. السلاسل النسبية هي نفسها تمامًا. مستويات الاهتزازات المختلفة لها طاقات مختلفة ، وبما أن الكتلة والطاقة مرتبطان بالعلاقة E = mc2 ، فإن الكتل المختلفة تتوافق مع حالات اهتزازية مختلفة.

سيكون من الرائع أن أقول إن تردد اهتزاز السلسلة يرتبط بطاقتها من خلال علاقة بسيطة من النوع E = hν ، كما كان الحال مع الفوتونات. للأسف ، هذا ليس بهذه البساطة. الكتلة الكلية للسلسلة تتكون من عدة مكونات. الأول هو الكتلة المتبقية من السلسلة ، والتي تقابل طاقة توتر السلسلة بين اثنين من النخالة D0. والثاني هو الكتلة المقابلة للطاقة الاهتزازية ، والتي تتكون بدورها من الطاقات الاهتزازية لجميع النغمات. تذكر أن الطاقة والكتلة مرتبطان بالعلاقة E = mc2. وأخيرًا ، المكون الثالث هو الكتلة المقابلة لطاقة التقلبات الكمية غير القابلة للاسترداد ، والتي تسمى تذبذبات نقطة الصفر. إن مصطلح "الاهتزازات الصفرية" يجعلنا نتذكر الحتمية الأساسية لتقلبات الكم. لذا: مساهمة طاقة نقطة الصفر في كتلة السلسلة ... هي سلبية! أوافق ، هذا غريب. غريب جدا. لإظهار مدى غرابة هذا ، سأعطي مثالاً. إذا قصرنا أنفسنا على وضع اهتزاز واحد للسلسلة ، فسوف نرى أن طاقة اهتزازات نقطة الصفر في هذا الوضع إيجابية. كل من النغمات العالية بشكل فردي يعطي مساهمة إيجابية أكبر في طاقة الأوتار. ولكن إذا جمعنا مساهمات جميع النغمات بشكل مناسب ، نحصل على رقم سالب. إذا كنت تعتقد أن هذا ليس سيئًا بما يكفي ، فهذه أخبار سيئة أكثر: لقد أخفيت جزءًا من الحقيقة بالقول إن مساهمة طاقة اهتزازات نقطة الصفر سلبية. كل هذه التأثيرات - كتلة الراحة والطاقة الاهتزازية والطاقة الاهتزازية ذات نقطة الصفر - تدخل تعبير الكتلة الإجمالية بمربعات قيمها. وإذا سادت طاقة اهتزازات نقطة الصفر في هذا المجموع ، فإن مربع الكتلة الإجمالية يكون سالبًا ، مما يعني أن الكتلة نفسها خيالية ، مثل جذر ناقص واحد.


قبل أن ترفض مثل هذا الهراء بسخط ، دعني أضيف أنه في نظرية الأوتار يتم تخصيص خط كامل من البحث للقضاء على المشكلة الموصوفة. باختصار ، المشكلة هي أن مربع كتلة السلسلة النسبية في أدنى حالة طاقة لها هو سلبي. السلاسل في هذه الحالة تسمى tachyons. نعم ، نعم ، هذه هي tachyons نفسها التي تواجه في كل سلسلة أبطال Star Trek. هذه بالتأكيد أخبار سيئة. في النموذج الذي وصفته ، سيكون من الممكن التخلص من مربع الكتلة السالب عن طريق سحب أغشية D0 التي ترتبط بها نهايات السلسلة ، بما يكفي بحيث تصبح طاقة توتر السلسلة أكبر من طاقة الاهتزاز بنقطة الصفر. ولكن عندما لا توجد أغشية D0 قريبة ، تظل السلسلة نفسها. حرمانًا من القدرة على التعلق بشيء ما ، يمكن أن يصبح مغلقًا ذاتيًا. الآن هي ليست ممتدة بين شيء وشيء ويمكن أن تتقلب ، ولكن ربما لا. الشيء الوحيد الذي لا يمكنها التوقف عن فعله هو التذبذب على المستوى الكمي. وكما حدث من قبل ، فإن التذبذبات الكمومية تحول مثل هذه السلسلة إلى tachyon ، وهو أمر سيئ للغاية للنظرية. وفقًا للمفاهيم الحديثة ، فإن tachyons غير مستقرة ، فهي أقرب إلى موازنة قلم رصاص على الحافة. يمكنك محاولة موازنة مثل هذا القلم ، لكن أي نفس خفيف سيقلبه. تشبه نظرية الأوتار التي تحتوي على tachyons نظرية تصف ملايين الأقلام الواقفة على مساحة ملء الحافة.

ومع ذلك ، فقد بالغت كثيرا. هناك حل لإنقاذ tachyons. افترض أن الحالة الأرضية لسلسلة tachyon تتوافق مع الكتلة الخيالية ومربعها: m2 <0 ، كما أن الطاقة الاهتزازية تساهم أيضًا في مربع الكتلة. باستخدام المجموعة الصحيحة وتسليم البطاقات بالطريقة اللازمة ، يمكنك التأكد من أن الكتلة الإجمالية للسلسلة هي صفر تمامًا. هذا أمر مشجع لأنه ، كما نعلم ، في العالم الحقيقي توجد جزيئات لا كتلة لها ، مثل الفوتونات أو الجاذبية. لذلك ، إذا كانت الأوتار تصف العالم الحقيقي حقًا ، فيجب أن تكون بلا كتلة ، أو بشكل أكثر صرامة ، يجب أن تكون بعض الحالات الكمية من الأوتار بلا كتلة.

يرجى ملاحظة أنك بحاجة إلى أخذ مجموعة البطاقات الصحيحة. مع هذا الاستعارة ، أردت أن أقول أننا بحاجة إلى الزمكان 26-الأبعاد. ربما كنت قد خمنت بالفعل أن كل شيء سيصل إلى هذا الخزي ، لذلك لن أعتذر. هناك العديد من الحجج المؤيدة لـ 26 بُعدًا ، لكن معظمها رياضيات بحتة ، وأخشى أنها لن تبدو مقنعة لغالبية القراء. الحجة التي سأقدمها أكثر جسدية. نود الحصول على حالات الكم من السلاسل الكمومية. نحن نعلم أن التذبذبات الكمية الصفرية "تدفع" m2 في الاتجاه السلبي. نحن نعلم أيضًا أن الأوضاع الاهتزازية "تدفع" m2 في الاتجاه المعاكس. لا تعتمد القيمة الدنيا المحتملة للطاقة الاهتزازية على أبعاد الفضاء ، في حين أن حجم الاهتزازات الصفرية الكمية يعتمد. دعونا نلقي نظرة عليه من هذا الجانب: عندما يتردد شيء ما - خيط بيانو أو أي شيء آخر - فإنه يفعل ذلك في اتجاه معين. تتأرجح سلسلة البيانو في الاتجاه الذي تصطدم به المطرقة. على سبيل المثال ، تتأرجح سلسلة البيانو لأعلى ولأسفل ، ولكن ليس إلى اليمين أو اليسار. يختار التمايل اتجاهًا واحدًا ويتجاهل الباقي. في المقابل ، تحدث اهتزازات نقطة الصفر الميكانيكية الكمومية في جميع الاتجاهات الممكنة ، وإضافة كل بعد جديد يضيف تقلبات كمية اتجاه آخر يمكن أن تحدث فيه التذبذبات. المزيد من الاتجاهات المحتملة للتذبذبات ، أو كما يطلق عليها ، درجات الحرية ، تعني عددًا أكبر من التقلبات ، مما يؤدي إلى مساهمة سلبية أكبر في m2. يبقى فقط لحساب كيفية اختيار المساهمات في الكتلة الإجمالية للأوضاع الاهتزازية واهتزازات صفر. اتضح أن نمطًا تذبذبًا واحدًا مع الحد الأدنى من قيمة الطاقة يتم تعويضه بواسطة تذبذب كمومي صفر 26 الأبعاد. انظر إلى هذا بتفاؤل ، لأن عدد القياسات اللازمة يمكن أن يكون غير متكامل! ماذا سنفعل ، على سبيل المثال ، بأبعاد ستة وعشرين ونصف؟

إذا لم تتقن أنواعًا مختلفة من التقلبات ، فلا تقلق. إنهم متشابهون للغاية. الفرق الوحيد بين الأوضاع الاهتزازية والاهتزازات الصفرية الكمية هو أن الأوضاع الاهتزازية قد تكون أو لا تكون موجودة ، بينما لا توجد اهتزازات صفر دائمًا. الاهتزازات الصفرية هي تلك الحركات الدنيا ، التي يتطلب وجودها مبدأ عدم اليقين. بالإضافة إلى الوضع الرئيسي ، توجد نغمات في اهتزازات السلسلة ، مما يمنح السلسلة خصائص ميكانيكية كمية جديدة. أفضل أن أتخيل أوضاعًا مختلفة في شكل نماذج ميكانيكية بسيطة ، مثل الاهتزازات الدائرية ، والاهتزازات في شكل ورقة البرسيم أو الاهتزازات الالتوائية. . , . , , -. , . — - .


, : , . , , . . 26- . . , , , . .

, 26 10. , . - . --, , . . -- , « », . , , - ˆ, ˆ. , . - . — . - , .

, . . -, . , , , , . , , , , , , - , , , , . , . , - , , . . . , . — .

»يمكن العثور على مزيد من المعلومات حول الكتاب على موقع الناشر على الويب
» المحتويات
» مقتطفات

20% —