نحن نفهم فيزياء الجسيمات: 8) كيف تتفاعل الجسيمات مع الحقول

فهم فيزياء الجسيمات:
1. الكرة في الربيع ، نسخة نيوتن
2. كرة كمومية على زنبرك
3. الأمواج ، نظرة كلاسيكية
4. الموجات ، المعادلة الكلاسيكية للحركة
5. موجات الكم
6. الحقول
7. الجسيمات هي كمية
8. كيف تتفاعل الجسيمات مع الحقول

كيف يعمل حقل هيجز:
1. الفكرة الرئيسية

في مقال سابق في السلسلة ، أوضحت أن جزيئات الطبيعة هي كمية من المجالات النسبية التي تلبي معادلات الحركة من الفئة 0 والفئة 1. لكن ما لم أقله حتى الآن ، لذا فإن هذا البيان ، لحسن الحظ ، صحيح جزئيًا فقط. المعادلات الحقيقية دائمًا ما تكون أكثر تعقيدًا قليلاً ، بحيث يبقى الترابط بين الجسيمات والحقول ، ولكن الظواهر والعمليات الأكثر تنوعًا تصبح ممكنة ، بما في ذلك ظهور الجسيمات بعد اصطدام الجسيمات الأخرى ، وانحلال الجسيمات في جسيمات أخرى ، وتناثر الجسيمات من بعضها البعض ، بالإضافة إلى تكوين أشياء مثيرة للاهتمام مثل البروتونات والنيوترونات والنوى والذرات. لن أتمكن من شرح كل هذا بالتفصيل ، ولكن في هذه المقالة سأقدم لك مقدمة لكيفية عمل كل شيء.

الاختلاف الرئيسي بين المعادلات ، التي أسميتها "class 0" و "class 1" ، والمعادلات المهمة للفيزياء الحقيقية ، هو أنه في المعادلات الحقيقية توجد مصطلحات إضافية تعتمد على مجالين أو أكثر ، وليس واحدًا فقط . هذا يعني ، دعنا نقول ، بدلاً من معادلة الفئة 0 للحقل النسبي Z (x، t) ، الذي يبدو

$$

$$d ^ 2Z / dt ^ 2 - c ^ 2 d ^ 2Z / dx ^ 2 = 0$$

بالنسبة للحقول الحقيقية ، تبدو المعادلات أكثر مثل هذا:

$$

$$d ^ 2Z / dt ^ 2 - c ^ 2 d ^ 2Z / dx ^ 2 = y ’Z (x، t) ^ 3 + y A (x، t) B (x، t)$$

عندما تكون y و y 'أرقامًا (عادةً ما تكون أقل من 1) ، فإن Z عبارة عن تدوين قصير لـ Z (x، t) و A (x، t) و B (x، t) زوج من الحقول الأخرى. في مثل هذه المعادلات ، يمكن للمرء أن يتوقع ظهور مصطلحات مثل A (x ، t) Z (x ، t) ، أو A (x ، t) ² Z (x ، t) ، أو Z (x ، t) ² ، أو حتى A (x، t) d ² Z / dt ² ، إلخ. يعتمد الأعضاء الذين يمكنهم الظهور والذين لا يمكنهم الظهور على تفاصيل الحقول المشاركة في العملية. القواعد صارمة ، لكنها مربكة إلى حد ما ، لذلك لن نتناولها الآن. بشكل عام ، من التجارب أنشأنا (وفهمنا من وجهة نظر نظرية) أنه في الطبيعة:

• أي مصطلح صالح من حيث المبدأ (الحفاظ على الشحنة الكهربائية أو مراسلات نسبية آينشتاين) يظهر في المعادلات ،
• ولكن الأعضاء الذين لديهم العديد من الحقول عادة ما يكونون صغار جدًا وغير مهمين مقارنة بالأعضاء الذين لديهم مجال واحد ، واثنين ، وأحيانًا ثلاثة حقول (الأعضاء التي تحتوي على مشتقات من الزمان أو المكان عادة ما تكون صغيرة).

لذلك ، في العمليات الفيزيائية الأكثر إثارة للاهتمام ، يمكن للمرء أن يركز على جميع المصطلحات الصالحة بمجال واحد أو اثنين أو ثلاثة.

القليل من المصطلحات. تسمى المصطلحات في المعادلات بالحقول الخطية في الدرجة الأولى. جميع المصطلحات في معادلاتنا من الدرجة 0 أو 1 كانت خطية. يُطلق على الأعضاء الذين لديهم حقلين أو ثلاثة حقول تربيعية أو مكعبة ؛ بشكل عام ، تسمى غير خطية. تظهر جميع الظواهر المثيرة للاهتمام في عالمنا بسبب المصطلحات غير الخطية في معادلات الحركة - أي تفاعل الحقول مع بعضها البعض ومعها. دعونا ندرس واحد منهم.

ظهور موجة جديدة من صدى الاثنين الآخرين

للحصول على فكرة عن كيف يمكن أن يصبح كل شيء مثيرًا للاهتمام ، نأخذ ثلاثة حقول ، A (x ، t) ، B (x ، t) ، C (x ، t) ، وموقف مبسط. افترض أن الحقلين A و B يفيان تقريبًا بمعادلات الفئة 0 (ويحتويان على كميات بلا كتلة) ، والحقل C يرضي معادلات الفئة 1 (يحتوي على موجات ذات تردد أدنى ν _min ، وبالتالي ، الكمية مع الكتلة m = h ν _min / c ² ، حيث h - ثابت بلانك). سنضيف أيضًا مصطلحات غير خطية إلى معادلاتها. على وجه التحديد ، مثل هذا (للإيجاز ، سنكتب "A" بدلاً من "A (x، t)" ، وهكذا ، c هي سرعة الضوء ، y هو رقم أقل عادةً من 1):

$$

$$d ^ 2A / dt ^ 2 - c ^ 2 d ^ 2A / dx ^ 2 = y BC \\ d ^ 2B / dt ^ 2 - c ^ 2 d ^ 2B / dx ^ 2 = y AC \\ d ^ 2C / dt ^ 2 - c ^ 2 d ^ 2C / dx ^ 2 = (2 \ pi \ nu_ {min}) ^ 2 C + y AB$$

طباعة دقيقة: أضفت مصطلحات غير خطية إلى جميع المعادلات الثلاث لأن وجود هذه المصطلحات في إحدى المعادلات وغيابها في الأخرى سيؤدي إلى تناقضات ؛ على سبيل المثال ، لن يتم الحفاظ على الطاقة. للعملية التي أصفها ، سنحتاج إلى النظر فقط في المصطلحات غير الخطية في معادلات الحركة للمجال C.

دعونا نرى ما يحدث مع هذه المجموعة من المعادلات إذا كانت موجة المجال A تفي بموجة المجال B. من حيث المبدأ ، يمكننا تخمين ذلك من خلال تطبيق طريقة الفحص الدقيق. إذا كانت هناك موجة في المجال A ، فإن A (x، t) تكون بالقرب من الصفر. عندما تتداخل موجات الحقول A و B مع بعضها البعض ، تصبح نتيجة ضرب A (x، t) و B (x، t) غير صفرية. ننتقل الآن إلى معادلة C: ترتبط التغييرات في الحقل C في الزمان والمكان (فصلان على الجانب الأيسر) بالمنتج A و B (أحد المصطلحات على الجانب الأيمن).

$$

$$d ^ 2C / dt ^ 2 - c ^ 2 d ^ 2C / dx ^ 2 = (2 \ pi \ nu_ {min}) ^ 2 C + y A B$$

لذلك حتى إذا كان الحقل C صفرًا عندما يصبح A (x، t) B (x، t) غير صفري ، فإن C (x، t) سيصبح قريبًا غير صفري في نفس القسم. باختصار ، نتيجة لاجتماع الأمواج A و B ، سيحدث اضطراب صغير في المجال C.

طباعة صغيرة: قد تكون مهتمًا بـ - بعد أن يصبح C غير صفري ، سواء أصبح المصطلح A (x، t) C (x، t) في معادلة الحركة للمجال. يتسبب في اضطراب إضافي للحقل B. الإجابة هي نعم ، ولكن هذا التأثير سوف حتى أصغر. حتى نتجاهله ، ونكتشف فيما بعد لماذا يستحق ذلك.

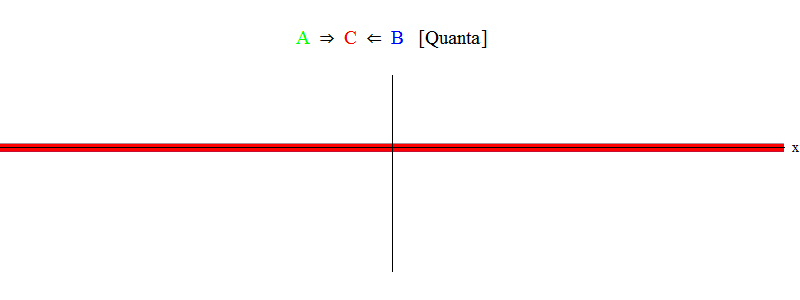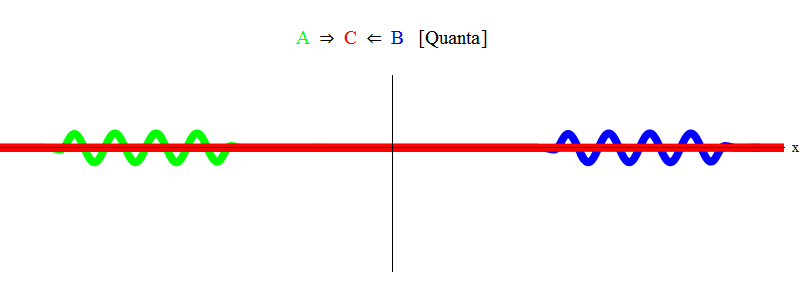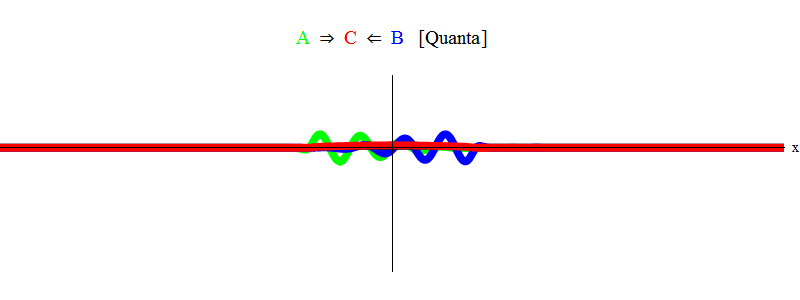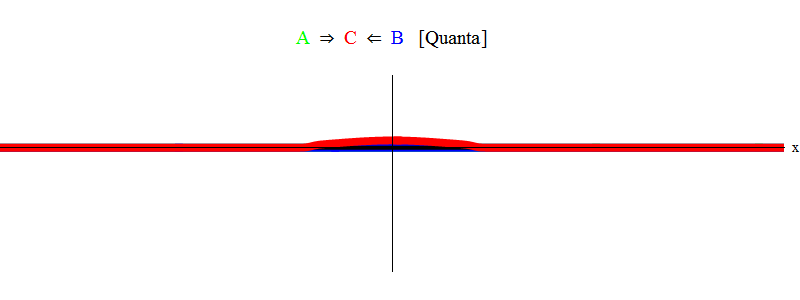
في الشكل. يوضح الشكل 1 موجة ذات تردد field في المجال A (أخضر) ، والتي تحدث مع موجة تردد ν في المجال B (أزرق). قمت بموازنة ترددات البساطة والتناظر. في وقت لاحق سنرى لماذا تأتي حالات أخرى لهذا. يمكن تقدير السرعة by من خلال ملاحظة الموجة الخضراء والخط العمودي الموجود عند نقطة واحدة في الفضاء والتأرجح مع الموجة.

يوضح المنتج البرتقالي أدناه المنتج A (x، t) B (x، t) ؛ يمكن ملاحظة أنه يصبح غير صفري عندما يتم فرض موجتين. كما يُلاحظ أنه يختلف باختلاف الوقت. يمكنك أن ترى (مقارنة مع شريط عمودي متذبذب) أن A (x، t) B (x، t) تتأرجح مرتين بسرعة. تذكر هذه الحقيقة الهامة. في الحالة العامة ، إذا كانت موجة التردد ν ₁ تفي بموجة تردد ν ₂ ، فإن منتجها سيتذبذب بتردد ν ₁ + ν ₂ . وشيء آخر: يمكنك ملاحظة أن اهتزازات AB لا تتحرك إلى اليمين أو اليسار ، فهي تبقى في مكانها. في وقت لاحق سنرى لماذا هذا مهم.


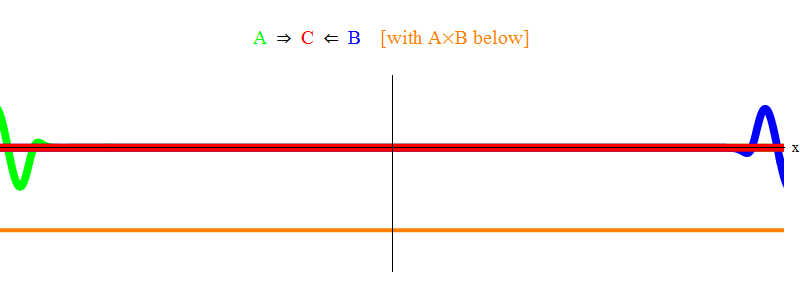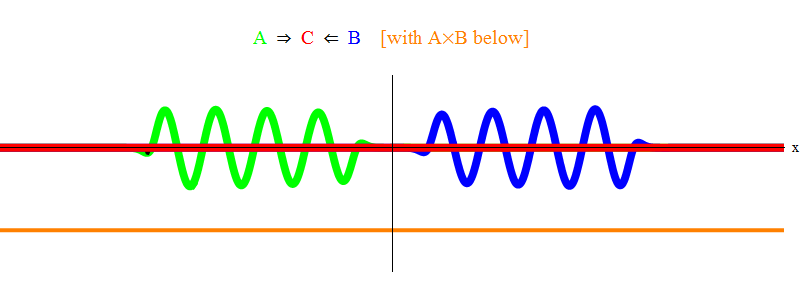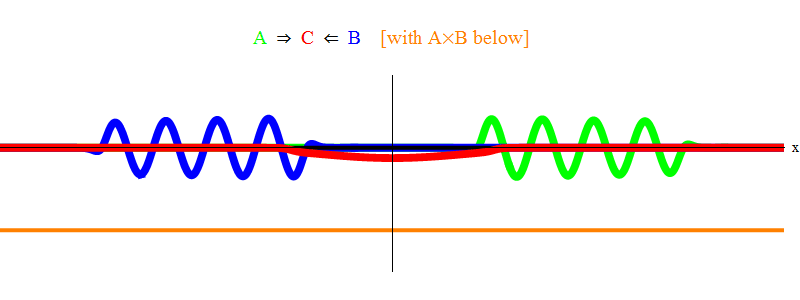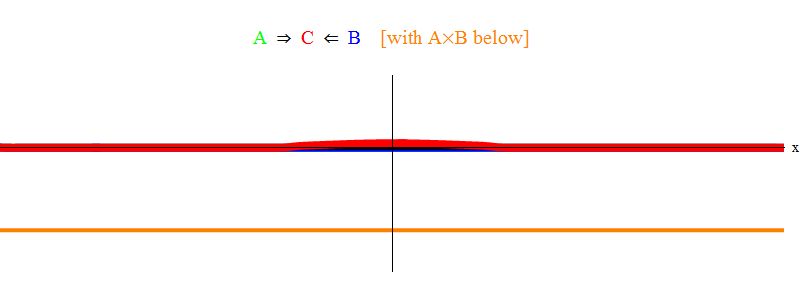التين. 1

كيف تؤثر القيمة غير الصفرية لـ AB على C؟ الجواب يعتمد بشكل كبير على التردد ν. أولاً سأقدم لك إجابة جاهزة ، ثم شرحًا تقريبيًا للسبب. هذا في الواقع صدى . الرنين هو ظاهرة متكاملة لجميع الاهتزازات (الاهتزازات) ، بما في ذلك الموجات. لقد وصفت بالفعل كيف تتأرجح الكرة في الربيع بتردد طبيعي ، وكيف يمكن أن تؤدي القوة الاهتزازية التي تدفع الكرة إلى الرنين إذا تزامن تردد تذبذب القوة مع التردد الطبيعي للكرة في الربيع.

بعد فهم الرنين ، سترى أن المجال C ، الذي يتأرجح مع الحد الأدنى من التردد والسرعة الأفقية الصفرية ، يتصرف مثل الكرة في الربيع ، و AB يتصرف مثل قوة متذبذبة تحاول جعل الكرة تتأرجح. لذلك ، تحدث ظاهرة الرنين إذا كان تردد الاهتزاز AB - 2ν - التردد الأدنى للحقل C - ν _min . وبشكل أكثر تحديدًا:

• إذا كانت 2 ν لا تساوي ν _دقيقة - إذا لم تكن القوة في الرنين - فعندئذ في المنطقة التي لا تساوي AB فيها صفر ، سيبدأ C في التذبذب بشكل غير منتظم ، مع سعة صغيرة.
• إذا كانت 2 ν = ν _دقيقة - إذا كانت القوة في الرنين - فإن C تتأرجح بسلاسة ، بسعة كبيرة ، في المنطقة التي لا تساوي AB فيها صفر ، وستستمر في التذبذب حتى عندما تصبح AB صفرًا مرة أخرى.

التين. 1 يظهر فقط حالة الرنين 2 ν = ν _دقيقة . يمكن ملاحظة أنه عندما تمر الموجة A عبر الموجة B ، فإنها تترك وراءها موجة ثابتة C تتأرجح بتردد ν _min . طباعة دقيقة: في الشكل. يتم عرض رسم تخطيطي ، وليس حلاً دقيقًا للمعادلات. سيكون للحل الدقيق العديد من الميزات المعقدة الصغيرة التي تلقي بظلالها على المعنى المادي الأساسي ، لذلك قمت بحذفها من أجل الوضوح. في وقت لاحق سننظر في وضع بدون صدى ، وهو أكثر تعقيدًا بكثير ، ولكنه أيضًا أكثر أهمية للفيزياء.

ظهور جسيم جديد من إبادة الاثنين الآخرين

لقد أوضحت لكم للتو أن المصطلحات غير الخطية AB في المعادلة C يمكن أن تؤدي إلى تراكب الموجات A و B لإنتاج تذبذبات المجال C إذا كان مجموع ترددات المجالين A و B يساوي الحد الأدنى لتردد المجال C. ولكن ماذا لو كانت هذه الموجات سعة صغيرة جدا؟ ماذا يمكن أن يحدث إذا التقى كم واحد من الحقل A بكمية واحدة من الحقل B؟

• إذا دخلت الترددات AB في الرنين مع المجال C ، فقد يحدث كم من المجال C ، أي جسيم حقيقي C ، وستختفي الكميات A و B - "تقضي".
• أيضًا ، يمكن للكميتين A و B ببساطة تمرير بعضهما البعض ، دون تكوين جسيم C.
• تشير قوانين ميكانيكا الكم إلى أن احتمالية إنشاء جسيم C متناسبة مع مربع y ، مضروبًا في AB في معادلة الحركة C.
• إذا لم تدخل الترددات في الرنين ، فلن يظهر الجسيم الحقيقي C. ومع ذلك ، قد يحدث اضطراب مؤقت في المجال C ، مثال على ما يسمى غالبًا "الجسيم الافتراضي" C ، وفي هذه الحالة قد تختفي الكميات A و B. ما هي نتيجة هذا الاضطراب؟ لقد وصفت هذه العملية جزئيًا في نهاية المقالة ، في قسم "ذيول".

هذه هي الحالة العامة للأشياء. دعونا نتعمق في التفاصيل.

ماذا تعني الجسيمات ، أي كمية الحقول أ ، ب ، ج ، أن تكون في صدى أم لا في صدى؟ من الجدير بالذكر أن طاقة الكم مرتبطة بترددها بسبب المعادلة E = h ν. لذا نترجم مناقشتنا للموجات إلى مناقشة للجسيمات.

افترض أن موجاتنا في المجالين A و B تتكون من كل كم. هذه الكميات بلا كتلة ، حيث أن A و B يفيان بمعادلات الفئة 0. وبشكل أكثر دقة ، فإن المصطلحات الخطية في معادلات الحركة هي نفسها معادلات الفئة 0. نظرًا لأن الكميتين A و B لهما نفس التردد ، فلديهما نفس الطاقة ، E = h ν. بما أن زخم الكم بدون كتلة هو p = E / c ، فإن الكمي A و B سيكون لهما قوة مساوية في الحجم إلى h h / c ، ولكن في الاتجاه المعاكس ، حيث يتحرك أحدهما إلى اليسار والآخر إلى اليمين. لذلك:

• الطاقة الكلية لكميتين معا ستكون 2 ساعة ونصف.
• سيكون الزخم الكلي للكمتين معًا صفرًا.

نظرًا لأنه يتم الحفاظ على الطاقة والزخم ، فإن الطاقة الإجمالية بعد اصطدام كميتين ستظل تساوي 2hν ، وسيظل إجمالي الوقت صفرًا.

في حالة الأمواج ، رأينا أنه نظرًا لأن معادلة C تحتوي على مصطلح من الشكل AB ، هناك صدى عندما يتزامن التردد AB (يعمل كقوة متأرجحة) مع الحد الأدنى للتردد C (يعمل مثل الكرة في الربيع). نترجم هذا البيان إلى الكم.

سيكون التردد AB 2 ν ، وبالتالي فإن طاقة المنتج A و B ، عندما تتكون الموجات A و B من كمية واحدة ، تساوي مجموع الطاقات A و B.

$$

$$E_ {AB} = ساعتان \ nu = E_A + E_B$$

الحد الأدنى للتردد C يساوي ν _min ، مما يعني أنه بالنسبة لمقدار ثابت للحقل C ، يكون الزخم 0 ، والطاقة

$$

$$E_C = h \ nu_ {min} = mc ^ 2$$

حيث m هي كتلة الكم C.

للرنين ، مطلوب 2 ν = ν _دقيقة ، أي:

$$

$$E_A + E_B = 2 h \ nu = h \ nu_ {min} = mc ^ 2 = E_C$$

باختصار ، يحدث الرنين عندما تكون مبالغ طاقات متساوية من الجسيمات A و B (في هذه الحالة تكون النبضات متشابهة في الحجم ومعاكسة للاتجاه) تكفي فقط لإنشاء جسيم ثابت C! في هذه العملية ، يتم القضاء على الجسيمات A و B - طاقتهما تذهب تمامًا في إنشاء الجسيم C. يظهر هذا (بشكل تخطيطي) في الشكل. 2 ، والتي تحتاج للمقارنة مع الشكل. 1.


التين. 2

المنطق

لقد عرضت عليك للتو العملية A + B → C. في شرحي ، استخدمت ثلاثة أنواع مختلفة من الجسيمات لتجنب الالتباس. لكن نفس الفكرة تسمح لعمليات النموذج A + A → C بالمرور (على سبيل المثال ، gluon + gluon → جسيم Higgs ، وهذه هي الطريقة التي يتم بها الحصول على جسيم Higgs في مصادم هادرون الكبير) وعمليات الشكل A + A * → C ، حيث A * - الجسيمات المضادة لـ A (على سبيل المثال ، quark + antiquark → Z-particle ، وهذه هي الطريقة التي يتم بها الحصول على الجسيمات Z عادة على LHC). من الضروري فقط تغيير التفاصيل الصغيرة ، لكن الجوهر يبقى كما هو.

عملية أخرى تمثل نفس الفكرة ، لا تنعكس إلا بمرور الوقت - انحلال الجسيمات. يتحلل جسيم هيجز إلى اثنين من الفوتونات أو جزيئات Z في كوارك ويحدث antiquark بشكل أساسي مثل الرسوم المتحركة في الشكل. 2 ، يسير في الاتجاه المعاكس.

ذيول

1. إذا كان المصطلح AB يزعج المجال C بدون رنين - إذا كان 2 ν ≠ ν _دقيقة - فماذا سيحدث؟ قد تتذكر أنه إذا قمت بدفع الأرجوحة مع الطفل بتردد خاطئ ، أو تطبيق قوة على الكرة في الربيع ، تتأرجح بتردد لا يتزامن مع التردد الطبيعي للاهتزازات ، فسوف تحصل على اهتزاز غير متساو مع سعة صغيرة. في السياق الحالي ، يحدث نفس الشيء مع الحقل C. سيتصرف الحقل C بطريقة أو بأخرى ، ولكن هذا لن يؤدي إلى ظهور كمية جيدة السلوك تتصرف بشكل جيد. هذا السخط السيئ هو أحد الأمثلة على ما يسمى "الجسيمات الافتراضية C" - لكن هذا ليس جسيمًا (كمًا لموجة المجال C) ، على الرغم من اسمه. تختلف كتلته عن كتلة الجسيم C ؛ يمكن أن يكون أكبر أو أصغر. على عكس الجسيم C ، فهو غير موجود بمفرده لفترة طويلة. ولا يفي بشروط السعة التي يجب أن تلبيها الكميات الحقيقية. بدلاً من ذلك ، على عكس الجسيم C ، الذي يوجد لبعض الوقت ، مع التين. 2 ، لا يوجد اضطراب غير متجاوب إلا عندما يتقاطع A.

لكن هذا لا يعني أنه لا يؤثر على أي شيء. على سبيل المثال ، يمكن أن يتسبب في ارتداد الجسيمات A و B من بعضها البعض.

$$

$$A_ \ rightarrow + B_ \ leftarrow → C_ {outrage} → A_ \ leftarrow + B_ \ rightarrow$$

بشكل عام ، في الفضاء ثلاثي الأبعاد ، يمكن أن يؤدي الارتداد أو التشتت إلى حقيقة أن A يتحرك في أي اتجاه و B يتحرك في الاتجاه المعاكس. تشمل الأمثلة على هذه العمليات تشتت الإلكترون والبوزيترون بسبب الفوتون الظاهري ، أو تشتت الكوارك وال antiquark بسبب الغلوون الافتراضي.

في وجود مجالات أخرى ، D و E ، تتفاعل مع C وتشارك في معادلة الحركة C

$$

$$d ^ 2C / dt ^ 2 - c ^ 2 d ^ 2C / dx ^ 2 = (2 \ pi \ nu_ {min}) ^ 2 C + y A B + y ’D E$$

قد تحدث عمليات أكثر إثارة للاهتمام:

_اضطراب A + B → C → D + E

هذا صحيح: يمكن أن تدمر الجسيمات A و B بفضل الجسيم الافتراضي C ، وتؤدي إلى ظهور جسيمات جديدة D و E. هذه هي الطريقة الثانية لإنشاء جسيمات جديدة! على سبيل المثال ، يمكن أن يتصادم الإلكترون مع بوزيترون ، ويبيد من خلال الفوتون الظاهري (تذكر أن هذا يعني "من خلال اضطراب في مجال الفوتون بتردد لا يتزامن مع الرنين") ، ويتحول إلى ميون وأنتيمون ، أو كوارك وعتيق. يمكن أن يتصادم الكوارك السفلي والعلامة القديمة العليا ، ويهلكان من خلال جسيم W الظاهري ، ويتحولان إلى إلكترون ومضاد للنترينو. أو يمكن أن يصطدم غلوينان ، ويبيدان من خلال غلوون افتراضي ، ويتحولان إلى كوارك علوي وعلامة antiquark العليا (هذه هي الطريقة الأكثر شيوعًا للحصول على الكواركات العلوية على LHC).

2. ماذا لو كانت الموجتان في المجالين A و B لها ترددات مختلفة ، ν _A و ν _B ؟ عند الترددات المناسبة ، قد تستمر الجسيمات C في الظهور ، لكن ظروف الرنين ستكون مختلفة ، ولن يكون الجسيم الذي تم إنشاؤه ثابتًا. دعونا نكتشف ذلك.

إذا كان لديهم ترددات مختلفة ، فسيكون هناك كميتان غير متصادمتين

• طاقات مختلفة $$$E_A = h \ nu_A$ و $$$E_B = h \ nu_B$
• نبضات مختلفة $$$p_A = + h \ nu_A / c$ و $$$p_B = - h \ nu_B / c$ (هنا ، بالإضافة إلى وسائل إلى اليمين ، ناقص إلى اليسار).

مجموع الزخم p _A + p _{B هو} الآن غير صفري. لكن الزخم مستمر. لذلك ، إذا كان يمكن أن يحدث الجسيم C نتيجة لإبادة الجسيمات A و B ، فسيكون له زخم p _C = p _A + p _B ، لذلك سوف يتحرك يسارًا أو يمينًا ، ولن يقف ساكنًا. إذا كانت ν _A > ν _B ، فسينتقل إلى اليمين ، وإلا إلى اليسار.

ما مقدار الطاقة المطلوبة لإنشاء جسيم متحرك C؟ لهذا ، هناك حاجة إلى طاقة أكثر من الطاقة الثابتة - مثل أي جسيم ضخم ، يجب أن تفي طاقته وزخمه

$$

$$E_C ^ 2 = (p_Cc) ^ 2 + (mc ^ 2) ^ 2$$

وهذا يعني أن E _C = mc ² إذا كان p _C = 0 أو أكثر إذا كان الزخم غير صفري. يخبرنا قانون الحفاظ على الطاقة والزخم أن:

$$

$$E_C = E_A + E_B$$

$$

$$p_C = p_A + p_B = E_A / c - E_B / c$$

من أين حصلت على المعادلة الأخيرة؟ بالنسبة للجسيمات عديمة الكتلة ، p = E / c ، ولجسيماتنا المتصادمة A و B ، فإن عزمها معاكس ، لذلك تختلف في الإشارة. عوض عن ذلك في المعادلة السابقة واحصل على:

$$

$$(E_A + E_B) ^ 2 = (E_A - E_B) ^ 2 + (mc ^ 2) ^ 2$$

يتم القضاء على المصطلحين E _A ² و E _B ² بشكل متبادل ، ونقل المصطلحين E _A E _B إلى اليسار ، نحصل على:

$$

$$4 E_A E_B = (mc ^ 2) ^ 2$$

بقسمة h ² واستخدام العلاقة m = hν _min / c ² ، نحصل على حالة الرنين:

$$

$$(2 \ nu A) (2 \ nu B) = \ nu_ {min} ^ 2$$

مما يقلل بشكل صحيح عندما ν _A = ν _B إلى معادلة جسيم متحرك C ، 2 ν = ν _min . إذا لم يتم استيفاء هذا الشرط ، فلا يمكن إنشاء الجسيم C. إذا كان راضيا ، فمن الممكن.

3. لاحظت أنه بنفس الطريقة التي تحتوي عليها معادلة الحركة للمجال C تحتوي على المصطلح AB ، فإن معادلة B تحتوي على المصطلح AC. تذكر هذه المعادلات:

$$

$$d ^ 2B / dt ^ 2 - c ^ 2 d ^ 2B / dx ^ 2 = y A C$$

$$

$$d ^ 2C / dt ^ 2 - c ^ 2 d ^ 2C / dx ^ 2 = (2 \ pi \ nu_ {min}) ^ 2 C + y A B$$

لذا ، إذا أدى تراكب الموجات A و B إلى ظهور موجة في المجال C ، مما يجعلها غير صفرية ، كما في الشكل. 1 ، هل نحن بحاجة إلى القلق بشأن حقيقة أن هذه الموجة الجديدة C تتداخل مع الموجة A الحالية وتؤدي إلى تغيير في المجال B؟ أجبت "نعم ، ولكن يمكننا تجاهل ذلك". يمكننا الإهمال بسبب مزيج من سببين.

أولاً ، بسبب العدد "y" الذي يظهر قبل مضاعفات AB و BC. التأثير على المجال C للعضو AB يتناسب مع y مضروبة في A مضروبًا في B. التأثير على المجال B للعضو AC يتناسب أيضًا مع y مضروبة في A مضروبًا في C ، ولكن هذا بدوره سيكون مساوياً لـ y مرتين من A مضروبًا في بمقدار A مضروبا في B. لذا ، طالما أن y أقل من 1 ، فإن y ² ستكون أقل من y ، وبالتالي فإن التأثير على B لعضو AC يكون صغيرًا مقارنة بالتأثير على C للعضو AB - على الأقل للموجات الصغيرة A و B. عادة ما تكون الموجات صغيرة: الجسيم A هو كم واحد للموجة في المجال A ؛ وبالتالي ، فإن الموجة A لها سعة صغيرة د.

من هنا يأتي السبب الثاني ، الغريب ، ولكن الأكثر إقناعاً: رأينا أنه إذا التقى الكم A واحد بكمية واحدة B وتحول إلى كم C واحد ، فستختفي الموجات A و B (تقضي). بعد إنشاء C ، لم يعد هناك أي موجة A ، وبالتالي فإن AC هي صفر ، أي أنه لا يوجد تأثير على المجال B.

: , , . 2, . 2 , y 1. . , , , . – , .