كتاب "الحد الأدنى المطلق. كيف تفسر نظرية الكم عالمنا ".

الفيزياء هي أكثر العلوم تعقيدًا ؛ فهي معقدة جدًا ورائعة جدًا. إذا تجاهلنا المكون الرياضي ، تصبح الفيزياء متاحة على الفور لأي شخص لديه فضول وخيال. سوف نفهم بسهولة مفهوم نظرية الجاذبية ، والاستغناء عن المعادلات الرياضية المعقدة. لذلك ، لكل من يفكر في ما يجعل التوت الأزرق والفراولة حمراء ؛ الذي يشك في أن الصوت ينتشر في شكل موجات ؛ أي شخص يتساءل عن سبب اختلاف سلوك الضوء عن أي ظاهرة أخرى في الكون ، عليك أن تفهم أن الأمر برمته في فيزياء الكم.

يقدم هذا الكتاب (ويزيل الغموض) عن العالم السحري لعلم الكم ، مثل أي كتاب آخر. تتحدث عن المفاهيم العلمية الأساسية ، من جزيئات الضوء إلى حالات المادة وأسباب التأثير السلبي لغازات الدفيئة ، وتكشف عن كل موضوع دون استخدام مصطلحات علمية محددة - أمثلة من الحياة اليومية العادية. بالطبع ، لا يمكن للكتاب عن فيزياء الكم الاستغناء عن الحد الأدنى من الصيغ والمعادلات ، ولكن هذا الحد الأدنى الضروري ، ومفهوم لمعظم القراء. وفقا للمؤلف ، يجب أن يكون كتابًا يعمم العلوم متاحًا ، ولكن ليس أقل من مستوى القارئ ، ولكن لرفع وتطوير فكره ومستواه الثقافي العام.

كرة المضرب الكمومية ولون الفاكهة

من الخصائص الرئيسية للإلكترونات المرتبطة بالذرات والجزيئات أن حالات طاقتها منفصلة. نقول أن طاقة الإلكترون يمكن قياسها كمًا ، أي أن الإلكترون المرتبط بذرة أو جزيء يمكن أن يكون له بعض قيم الطاقة المحددة فقط. تتغير الطاقة تدريجياً ، وهذه الخطوات لها أحجام منفصلة معينة. حالات الطاقة مثل السلالم. يمكنك الوقوف على خطوة واحدة أو الانتقال إلى الخطوة التالية الأعلى. ومع ذلك ، من المستحيل الوقوف في منتصف الطريق بين الخطوتين. غالبًا ما تسمى قيم الطاقة المنفصلة أو الكمية مستويات الطاقة. على عكس السلالم العادية ، عادة ما تكون الفترات الفاصلة بين مستويات الطاقة ليست هي نفسها.

يعتبر حساب الحالات الإلكترونية للجزيئات مجالًا مهمًا للبحث الكمي الحديث. تسمى هذه المنطقة كيمياء الكم. هذه الحسابات تجعل من الممكن الحصول على مستويات الطاقة الكمية للإلكترونات في الجزيئات (مستويات الطاقة) ، وكذلك لحساب بنية الجزيئات. يعطي حساب بنية الجزيء المسافة بين الذرات ومواقع جميع الذرات في الجزيء بدقة محدودة فقط من خلال مبدأ عدم اليقين. وبالتالي ، فإن الحسابات الميكانيكية الكمومية تجعل من الممكن تحديد حجم وشكل الجزيئات. مثل هذه الحسابات مهمة لفهم المبادئ الأساسية لربط الذرات بالجزيئات وبناء جزيئات جديدة. مع تطور نظرية الكم وظهور المزيد والمزيد من أجهزة الكمبيوتر القوية والمعقدة القادرة على حل المشكلات الرياضية الشاقة ، يمكن دراسة المزيد والمزيد من الجزيئات الكبيرة باستخدام طرق كيمياء الكم. تطوير الأدوية من أهم تطبيقات نظرية الكم. يمكن تصميم الجزيئات بحيث يكون لها الحجم المطلوب و "الملاءمة" في الشكل لمواضع محددة من البروتينات أو الإنزيمات.

تتطلب كيمياء الكم حسابات شاقة للغاية. حتى بالنسبة لأبسط ذرة هيدروجين ، فإن الحسابات الميكانيكية الكمومية معقدة للغاية من الناحية الرياضية. تتكون ذرة الهيدروجين من إلكترون واحد مرتبط ببروتون واحد. البروتون ، وهو نواة ذرة الهيدروجين ، هو جسيم مشحون بشكل إيجابي ، والإلكترون مشحون بشكل سلبي. إن جذب إلكترون ذي شحنة سالبة إلى بروتون موجب الشحنة يحملهما معًا ، ممسكًا ذرة الهيدروجين معًا. لن يتم عرض تفاصيل حساب مستويات الطاقة لذرة الهيدروجين هنا ، ولكن في الفصول التالية سننظر في بعض ميزات نتائج هذه الحسابات. إنها تعطي مستويات الطاقة لذرة الهيدروجين ووظائفها الموجية. إن وظائف الموجة ، أي موجات اتساع الاحتمال لذرة الهيدروجين ، هي نقطة البداية لفهم جميع الذرات والجزيئات. الذرات والجزيئات معقدة لأنها أنظمة ثلاثية الأبعاد صغيرة للغاية ، ومن الضروري أن تأخذ في الاعتبار كيفية تفاعل البروتونات والإلكترونات مع بعضها البعض.

جسيم في صندوق - حالة كلاسيكية

هناك مهمة بسيطة للغاية تتعلق بموضوعنا. تُعرف باسم مشكلة الجسيمات في صندوق. لا يتطلب حل رياضيات معقدة لحلها ، لكن هذا الحل يسمح لنا بتوضيح الخصائص المهمة للإلكترونات المرتبطة ، على سبيل المثال ، تحديد مستويات الطاقة وطبيعة الإلكترونات الشبيهة بالموجات في الحالات المقيدة. قبل تحليل طبيعة الإلكترون في صندوق أحادي البعد للأحجام الذرية ، نناقش المشكلة الكلاسيكية في ملعب مثالي أحادي البعد للكرة المضرب لتحديد الاختلافات بين الأنظمة الكلاسيكية (الكبيرة) والميكانيكية الكمومية (الصغيرة للغاية).

في الشكل. 8.1 يصور "الصندوق" المثالي. هو أحادي البعد. تعتبر جدرانها عالية بشكل لا نهائي ، ضخمة للغاية ولا يمكن اختراقها تمامًا. لا يوجد هواء داخل الصندوق لمقاومة الحركة. في الشكل ، يتم تعيين داخل الصندوق Q = 0 ، أما الخارج - Q = ∞. قيل في وقت سابق أن الجسيم يسمى مجانا ولا قوة تعمل عليه. تنشأ القوى عندما يتفاعل الجسيم مع شيء ما. على سبيل المثال ، يمكن أن يتفاعل الجسيمات المشحونة سلبًا ، مثل الإلكترون ، مع البروتون الموجب الشحنة. التفاعل في شكل جاذبية بين الجسيمات المشحونة بشكل متعاكس سيولد قوة تعمل على الإلكترون. عند التحكم في الإلكترونات في CRT (انظر الشكل 7.3) ، يولد المجال الكهربائي قوة تعمل على الإلكترونات وتجبرها على تغيير الاتجاه.

يُطلق على قياس تفاعل الجسيم مع شيء يؤثر عليه ، مثل المجال الكهربائي ، جهد وله بُعد طاقة. في المستقبل ، سيتم التعبير عن الإمكانات بالحرف Q. داخل المربع ، Q = 0 ، كما هو الحال في الجسيمات الحرة. هذا يعني أن الجسيم لا يتفاعل مع أي شيء داخل الصندوق. لا توجد حقول كهربائية أو مقاومة الهواء. ومع ذلك ، خارج الصندوق ، Q = ∞. الإمكانات اللانهائية تعني أن الجسيم يجب أن يكون لديه طاقة لانهائية لكي يكون في مناطق خارج الصندوق. التعبير Q = just هو مجرد طريقة لإضفاء الطابع الرسمي على القول بأن جدران الصندوق مثالية. لا يستطيع الجسيم اختراق الجدران أو القفز فوقها ، مهما كانت طاقته كبيرة. إذا وضعت جسيمًا في مثل هذا الصندوق ، فلا يمكن أن ينزلق وسيبقى دائمًا بداخله. بهذا المعنى ، يتم قفل الجسيم في صندوق. يمكن أن يكون في منطقة ذات مساحة L ، ولكن في أي مكان آخر.

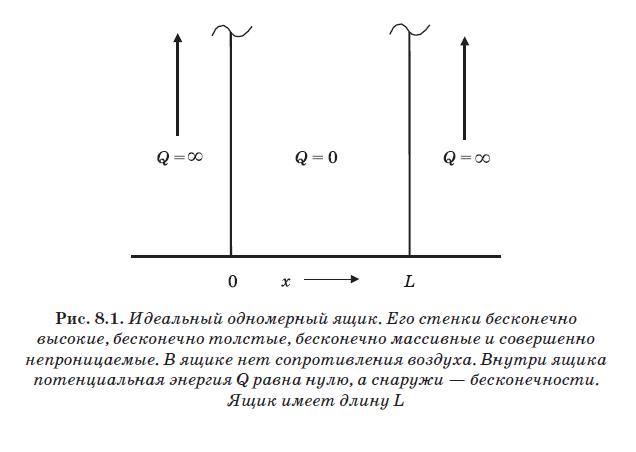
في الشكل. يوضح الشكل 8.2 كرة للعب كرة المضرب ، ترتد عن جدران ملعب كرة مضرب كلاسيكي كبير (كبير). كما سبق ذكره ، فإن هذه الجدران مثالية ، ولكن لا توجد مقاومة جوية في الداخل. بالإضافة إلى ذلك ، فإن الكرة مثالية أيضًا ، أي أنها تتمتع بمرونة مطلقة. عندما تصطدم الكرة بالجدار ، تنقبض مثل النابض وتستقيم مرة أخرى ، مما يتسبب في ارتدادها. الكرات الحقيقية ليست مرنة تمامًا. عندما يتم ضغط الكرة عند الاصطدام ، لا يتم طرد كل الطاقة التي تنفق في ضغطها من الحائط. يذهب جزء من الطاقة المستهلكة في ضغط الكرة لتسخينها. ومع ذلك ، سننظر هنا في الكرة مرنة تمامًا. عند ضرب الحائط ، يتم إنفاق كل الطاقة الحركية للكرة ، مما يؤدي إلى ضغطها ، على دفع الكرة بعيدًا عن الجدار. لذلك ، فإن سرعة الكرة قبل الاصطدام بالجدار تساوي سرعة ارتدادها بعد الاصطدام.

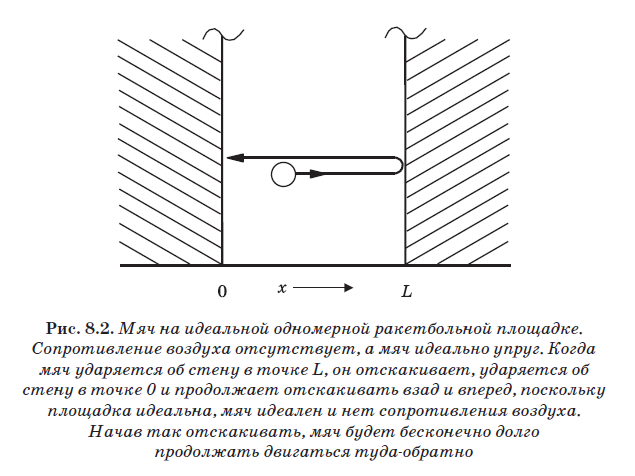
على هذه الأرض المثالية لكرة المضرب ، ترتد الكرة من على الجدران دون أي فقدان للطاقة. بالإضافة إلى ذلك ، لا توجد مقاومة للهواء ولا الجاذبية. لذلك ، ستتحرك الكرة دائمًا ذهابًا وإيابًا ، مما يعكس الجدران. يضرب الجدار عند النقطة L ، يرتد ، يصطدم بالجدار عند النقطة 0 ، يرتد مرة أخرى ويستمر في التحرك ذهابًا وإيابًا. داخل الصندوق ، بما أن الإمكانات صفر (انظر الشكل 8.1) ، لا توجد قوى تعمل على الكرة. لذلك ، فإن طاقتها حركية بحتة:

حيث m هي كتلة الكرة ، و V هي سرعتها. إذا تعرضت الكرة لتأثيرات خارجية ضعيفة ، فستصبح سرعتها أقل قليلاً وستنخفض قيمة Ek أيضًا بشكل طفيف. في كرة المضرب المثالية هذه ، يمكن أن تتغير الطاقة باستمرار. يمكن أن تزيد قيمة Ek أو تنقص بشكل تعسفي اعتمادًا فقط على قوة التأثير على الكرة.

ميزة أخرى مهمة في كرة المضرب الكلاسيكية هي القدرة على إيقاف الكرة بحيث تكون بلا حراك على الأرض. في هذه الحالة ، تكون سرعته صفرًا: V = 0. وبما أن V = 0 ، ثم Ek = 0. في V = 0 ، يكون الزخم أيضًا صفرًا ، حيث p = mV ، لذلك نحن نعرف الزخم تمامًا. إذا كانت الكرة على الأرض (V = 0) ، فسيكون موضعها معروفًا. إذا أشرنا إلى هذا الموضع x (انظر الشكل 8.2) ، فإن قيمة x ستكون في النطاق من 0 إلى L. لا يمكن أن تأخذ قيمة x أي قيم أخرى ، لأن الكرة في الملعب (في المربع) ولا يمكن أن تكون خارج من للجدران المثالية. يمكن وضع الكرة في موضع معين x على أرضية الملعب ، ومن ثم سيصبح موضعها معروفًا بالتأكيد. هذه خاصية ملعب مجهرية ، حتى مثالية. هذا نظام كلاسيكي ، ويمكن للمرء فيه أن يعرف بدقة وفي نفس الوقت الزخم p والموضع x.

يبلغ طول ملعب كرة المضرب 12 م ، ويبلغ قطر الكرة 5.6 سم ، ويبلغ وزنها حوالي 0.04 كجم. من الواضح أن لعبة كرة المضرب توصف بالميكانيكا الكلاسيكية. بمساعدة الضوء ، يمكنك متابعة ارتداد الكرة ذهابًا وإيابًا دون التأثير عليها.

الجسيمات في صندوق - حالة الكم

ما الذي سيتغير إذا انتقلنا الآن إلى النظر في كرة المضرب الكمومية؟ لا يزال الموقع مثاليًا ، ولكن الآن لا يبلغ طوله 12 م ، ولكن 1 نانومتر (10-9 م). بالإضافة إلى ذلك ، يحتوي الجسيم على كتلة إلكترون تبلغ 9.1 10-31 كجم ، وليس 0.04 كجم. وبالتالي ، هذه هي مشكلة الجسيمات الكمومية في صندوق.

يمكننا القول على الفور أن أصغر طاقة لجسيم كمي في صندوق بحجم النانومتر لا يمكن أن تكون صفراً. في مجال كرة المضرب الكلاسيكية ، تكون سرعة الكرة V ممكنة ، والتي تساوي الصفر ، مما يعني أن الدافع p = mV يمكن أن يكون صفرًا أيضًا. بالإضافة إلى ذلك ، فإن موضع الكرة × له معنى محدد بوضوح. على سبيل المثال ، قد تظل الكرة ثابتة (V = 0) بالضبط في منتصف الملعب ، وهو ما يتوافق مع x = L / 2. في هذه الحالة ، بالنسبة إلى كرة المضرب الكلاسيكية ، ∆p = 0 و ∆x = 0. لا تتوافق قيمة المنتج ∆x∆p = 0 مع مبدأ عدم اليقين Heisenberg ، وهو أمر طبيعي ، لأننا نتحدث عن النظام الكلاسيكي. ومع ذلك ، فإن الجسيم الصغير تمامًا في صندوق بحجم النانومتر هو كائن كمي ويجب أن يخضع لمبدأ عدم اليقين ، الذي ينص على أن ∆x∆p ≥ h / 4. إذا كانت V = 0 و x = L / 2 ، فإننا نعرف كل من x و p ، مما يعني أن ∆x∆p = 0 ، كما هو الحال في كرة المضرب الكلاسيكية. بالنسبة للنظام الكمي ، هذا غير ممكن. وبالتالي ، لا يمكن أن تكون V مساوية للصفر. لا يمكن أن يبقى الجسيم بلا حراك عند نقطة معينة. وإذا كانت قيمة V غير صفرية ، فلن تكون قيمة Ek مساوية للصفر. يقول مبدأ عدم اليقين أن أصغر طاقة في كرة المضرب الكمومية لا يمكن أن تكون صفراً. كرة الكم تبقى أبدا بلا حراك.

قيم طاقة الجسيمات الكمومية في صندوق

ما الطاقة التي يمكن أن يمتلكها الجسيم الكمومي في صندوق بحجم النانومتر؟ يمكن الإجابة على هذا السؤال دون حسابات معقدة ، لكننا نحتاج أولاً إلى العودة إلى الموجات مرة أخرى. تحدثنا في الفصل السادس عن الدوال الموجية للجسيمات الحرة. وظيفة الموجة لجسيم حر مع زخم معين p هي موجة تمتد في جميع أنحاء الفضاء. وبالتالي ، فإن الإلكترون ذو الزخم المحدد تمامًا هو موجة محددة ، تغطي المساحة بأكملها. إن احتمال اكتشاف الإلكترون الحر هو نفسه في كل مكان. مثل هذا الإلكترون لديه طاقة حركية محددة جيدًا Ek = 1 / 2mV2 ، لأنه يحتوي على زخم محدد جيدًا p = mV.

يشبه الإلكترون في صندوق النانومتر الجسيمات الحرة فيما يتعلق بالمنطقة الداخلية للصندوق ، حيث Q = 0. لا توجد إمكانات داخل الصندوق ، وبالتالي لا توجد قوى تعمل على الجسيم. في هذا الصدد ، يشبه إلى حد كبير الجسيمات الحرة ، التي لا تعمل عليها أي قوى أيضًا. ومع ذلك ، هناك فرق مهم بين الجسيم في الصندوق والجسيمات الحرة - هذه هي جدران الصندوق. الإلكترون الموجود في الصندوق موجود داخل الصندوق فقط. لا تسمح الطبيعة المثالية للمربع بوظيفة الموجة للانتشار في كل المساحة. الجسيم داخل الصندوق ولا يمكن أن يكون بالخارج أبدًا. تحدد دالة الموجة سعة احتمال اكتشاف جسيم في منطقة معينة من الفضاء. هذا هو تفسير بورن لدالة الموجة. إذا كان من الممكن اكتشاف إلكتروننا فقط داخل الصندوق وليس بالخارج أبدًا ، فيجب أن يكون احتمال اكتشافه في الصندوق محدودًا ، وخارجًا - صفر. إذا كان احتمال العثور على جسيم خارج الصندوق صفرًا ، فيجب أن تكون الدالة الموجية صفرًا في جميع النقاط خارج الصندوق.

لذلك ، توصلنا إلى استنتاج مفاده أن وظيفة الموجة للجسيم في صندوق تشبه وظيفة الموجة للجسيم الحر ، ولكن يجب أن تكون وظيفة الموجة صفر خارج الصندوق. في تفسيره لطبيعة دالة الموجة الكمومية الميكانيكية ، فرض بورن بعض القيود المادية على الشكل الذي يمكن أن تتخذه دالة الموجة. أحدها هو أن دالة الموجة الجيدة يجب أن تكون مستمرة. هذا الشرط يعني أن دالة الموجة يجب أن تتغير بسلاسة من مكان إلى آخر. لا يمكن أن يؤدي التغيير البسيط في الموقف إلى قفزة غير متوقعة في الاحتمال. هذه فكرة بسيطة للغاية. إذا كان احتمال اكتشاف جسيم في منطقة صغيرة جدًا من الفضاء ، على سبيل المثال ، 1٪ ، فإن إزاحة قيمة صغيرة لا يمكن تصورها لا يمكن أن تجعل فجأة احتمال اكتشاف جسيم يساوي 50٪. هذا واضح من صور حزم الموجة في الشكل. 6.7. يختلف الاحتمال بسلاسة من مكان إلى آخر. هذا يسمح لنا بإضافة شيء ما إلى وصف وظائف الموجة للجسيم في صندوق ، بالإضافة إلى حقيقة أنها موجات ذات سعة محدودة داخل الصندوق وسعة صفرية في الخارج. نظرًا لأن وظيفة الموجة يجب أن تكون مستمرة ، يجب أن يكون لها اتساع صفري مباشرة عند الجدار الصندوقي من الداخل لتتوافق مع اتساع الصفر لوظيفة الموجة خارج الصندوق.

في الشكل. 8.3 يوضح الانقطاع (المحظور) لوظيفة الموجة داخل الصندوق. يشار إلى الدالة الموجية (الحرف اليوناني "fi"). يمثل المحور الرأسي سعة دالة الموجة. يشير الخط المتقطع إلى مستوى الصفر. يمكن أن تتقلب الدوال الموجية ، وهي موجات اتساع الاحتمال ، بين القيم الموجبة والسالبة. الدالة الموجية الموضحة في الشكل. 8.3 ، بالقرب من قيم الجدران غير 0. ومع ذلك ، يجب أن تكون دالة الموجة صفر خارج الصندوق ، أي أن قيم x أقل من 0 وأكثر من L ، يجب أن تكون صفرًا. في الشكل ، تقفز وظيفة الموجة بشكل غير متوقع من قيمة غير صفرية بالقرب من الجدار داخل الصندوق إلى قيمة صفرية مباشرة خلف الجدار خارج الصندوق. وبالتالي ، فإن الدالة الموجية الموضحة في الشكل. 8.3 غير صالح لأنه غير مستمر. لا يمكن أن تمثل هذه الوظيفة جسيمًا كميًا في صندوق.

يجب أن يكون لدالة الموجة قيمة صفرية عند الجدران

لكي تكون وظائف الموجة التي تمثل الجسيم في الصندوق مقبولة جسديًا ، يجب أن تكون قيمها على الجدران صفرًا ، وبعد ذلك لن تواجه فجوة على الجدران. ليس من الصعب تحقيق هذا الشرط. تتقلب الدالة الموجية بين القيم الموجبة والسالبة. في كل مرة ، يمر من القيم الموجبة إلى السلبية أو من السلبية إلى الإيجابية ، يمر عبر الصفر. في الواقع ، يتم فصل نقاط الصفر عن بعضها البعض بمقدار نصف الطول الموجي. لذلك ، للحصول على وظائف موجية جيدة لجسيم في صندوق ، يجب أن نختار الموجات التي يسمح طولها بتكديسها في الصندوق بحيث تقع نقاط الصفر على الجدران فقط.

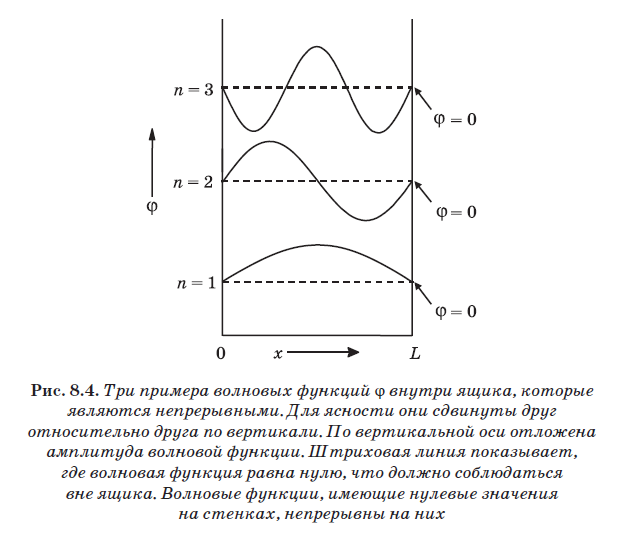
في الشكل. 8.4 يوضح ثلاثة أمثلة للموجات المناسبة لدور وظائف الموجة للجسيم في صندوق. تم تعيين الجزء السفلي منهم n = 1 ويتكون من نصف موجة واحدة. يبدأ على اليسار عند السعة 0 ، ويمرر الحد الأقصى ثم ينخفض ​​مرة أخرى إلى الصفر على الحائط عند النقطة L. تتكون الموجة التالية ، الموجودة أعلاه والمعلمة n = 2 ، من تذبذب كامل. يبدأ أيضًا عند الجدار الأيسر عند السعة 0 ، ويمرر ذروة موجبة ، ويعود إلى الصفر ، ثم يتبعه ذروة سالبة ويعود إلى الصفر على الحائط عند النقطة L. تحتوي الموجة المشار إليها بـ n = 3 على فترة ونصف. أي موجة تحتوي على عدد صحيح من نصف الموجات ، أي 1 ، 2 ، 3 ، 4 ، 5 ، وما إلى ذلك ، نصف طول الموجة ، وتقع بحيث تبدأ عند صفر على اليسار وتنتهي عند صفر على اليمين ، مناسبة.

القيمة n هي عدد نصف موجات دالة موجية معينة. بالنسبة إلى n = 1 ، يكون الطول الموجي 2L ، لأن طول الصندوق هو L ، ويقابل n = 1 نصف طول الموجة. بالنسبة إلى n = 2 ، يكون الطول الموجي L ، حيث يتم وضع طول موجة واحد بالضبط بين الجدران. بالنسبة إلى n = 3 ، يتم وضع ثلاث موجات نصف بين الجدران ، أي 1.5 = L. في هذه الحالة = L / 1.5 ، أي = 2 لتر / 3. لاحظ أنه تم العثور على قاعدة عامة هنا: = 2L / n ، حيث n عدد صحيح. بالنسبة إلى n = 1 نحصل على = 2L ، ل n = 2 - = 2L / 2 ، ل n = 3 - = 2L / 3 ، إلخ.

»يمكن العثور على مزيد من المعلومات حول الكتاب على موقع الناشر على الويب
» المحتويات
» مقتطفات

لقراء هذه المدونة ، خصم 20 ٪ على القسيمة - Fire