كيف يعمل حقل هيجز: 2) لماذا هو حقل هيجز في المتوسط ​​غير صفري

كيف يعمل حقل هيجز:

1. الفكرة الرئيسية
2. لماذا متوسط ​​حقل هيجز غير صفري
3. كيف يظهر جسيم هيجز
4. لماذا يعد حقل هيجز ضروريًا

كيف أن حقل هيجز في الطبيعة ليس له متوسط ​​قيمة صفر ، في حين أن حقول الطبيعة الأخرى (التي تبدو أولية) التي نعرفها لا تحتوي على صفر؟ [طباعة صغيرة جدًا: تُسمى الحقول الأخرى ، باستثناء مجال الجاذبية من أدنى مستوى ، بالمقياس ، وهذا يسمح لك بتحديد وجود المكان والزمان].

أولاً ، لا يمكن أن تحتوي حقول الفرميون على قيمة كبيرة غير صفرية ثابتة في الطبيعة. هذا يرجع إلى الفرق بين الفرميونات والبوزونات. يمكن أن يكون البوزون في المتوسط ​​غير صفري ، لكن الفرميونات لا تستطيع ذلك. لذا يمكنك نسيان الإلكترونات (وأبناء عمومتها الميونات والتاو) ، حول النيوترينوات والكواركات. طباعة صغيرة: يمكن للفرميونات أن تتزاوج مع بعضها البعض أو مع مضاد مضاد لها وتصنع بوزونات مركبة ، والتي يمكن أن تكون في المتوسط ​​غير صفرية. هذا هو الحال بالنسبة للكواركات العلوية والسفلية ولآثارها القديمة ، وللإلكترونات في الموصل الفائق. لكن هذه قصة طويلة ، ولا تهمنا مباشرة.

ماذا عن مجالات الفوتونات والغلوونات W و Z؟ هذه كلها بوزونات. من حيث المبدأ ، يمكن أن يكون لهذه الحقول متوسط ​​ثابت غير صفري على الكون. لكن التجارب ، وليس النظرية ، تقول إن الأمر ليس كذلك. ستؤدي القيمة الكبيرة غير الصفرية للمجال الكهربائي إلى ظهور تأثيرات مختلفة ، والتي لا نلاحظها. وأهم هذه الانتهاكات هو انتهاك الثبات الدوراني على نطاق واسع. المجال الكهربائي هو ناقل (spin-1) ، يشير في اتجاه معين ، لذلك إذا كان غير صفري ، فيجب أن يكون الاتجاه الذي تشير إليه هذه القيمة مختلفًا عن جميع المجالات الأخرى. (الشكل 1 ، أسفل اليسار).


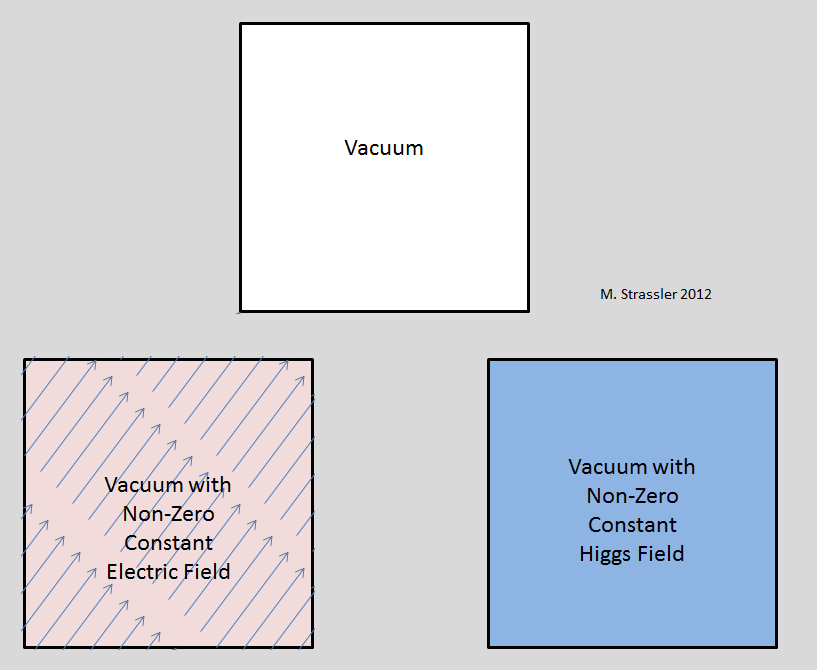التين. 1

حقل هيجز هو عددي (تدور -0) ، ولا يشير إلى أي مكان. من بين المجالات العددية الأخرى (لا الابتدائية ولا النسبية) ، يمكننا إعطاء أمثلة على مجال كثافة الهواء ، ومجال الضغط داخل الأرض ، ودرجة حرارة المحيط. في كل نقطة في المكان والزمان ، تكون الكثافة أو الضغط أو درجة الحرارة مجرد رقم ، والمجال الكهربائي رقم واتجاه. لذا ، إذا كان حقل هيجز يحتوي على قيمة غير صفرية ، فلن ينشأ اتجاه مفضل - الشكل. 1 ، أسفل اليمين. ما هو أكثر غرابة (لأنه نسبي) ، لا يولد حقل هيجز أي إطار مرجعي مفضل. بالنسبة لكثافة الهواء ، هناك نظام مرجعي مفضل ، لأنك إما تستريح نسبة إلى الهواء أو تتنقل خلاله. لكن الأمر ليس كذلك بالنسبة لحقل هيجز. جميع المراقبين يستريحون بالنسبة له. لذلك ، فإن نجاح آينشتاين SRT ، الذي يصف جميع أنواع الظواهر ، لا يتعارض مع وجود مجال عددي نسبي ذي قيمة غير صفرية ، مثل حقل هيجز. باختصار ، في وجود حقل هيجز غير صفري ، يتصرف الفراغ تمامًا كما يتصرف عند H = 0 ؛ يمكن الكشف عن وجودها فقط من خلال التأثير على كتلة الجسيمات (أو من خلال شيء أكثر إثارة ، على سبيل المثال ، استخدام LHC لإنشاء جسيمات هيجز).

إن أبسط طريقة لحقل هيجز هي الحفاظ على قيمة غير صفرية في جميع أنحاء الكون إذا كان لها قيمة توازن غير صفرية H ₀ متضمنة في معادلة الحركة من الفئة 1:

$$

$$d ^ 2H / dt ^ 2 - c ^ 2 d ^ 2H / dx ^ 2 = - (2 \ pi \ nu_ {min}) ^ 2 (H - H_0)$$

(يجب أن تكون الفئة 1 ، وليس الفئة 0 ، لأسباب ستصبح واضحة لنا بعد مناقشة جسيم هيجز). في الواقع ، الوضع أكثر تعقيدًا بعض الشيء. ستبدو المعادلة الصحيحة كما يلي:

$$

$$d ^ 2H / dt ^ 2 - c ^ 2 d ^ 2H / dx ^ 2 = a ^ 2 H - b ^ 2 H ^ 3$$

حيث يكون a و b ثوابتين (مربعاتهما موجبة! لاحظ علامة الجمع أمام ² H ، وقارنها بالناقص في المعادلة السابقة) ، والتي سنتعرف عليها لاحقًا. يمكن إعادة كتابة هذا على النحو التالي:

$$

$$d ^ 2H / dt ^ 2 - c ^ 2 d ^ 2H / dx ^ 2 = - b ^ 2 H (H ^ 2 - [a / b] ^ 2)$$

إذا كانت H (x، t) ثابتة في المكان والزمان ، فإن dH / dt = dH / dx = 0 ، وبالتالي

$$

$$0 = - b2 H (H2 - [a / b] ^ 2)$$

(عندما يكون H (x، t) ثابتًا في x و t) ، ولديه حلول (في الوقت الحالي ، سنبسط كل شيء بشكل كبير):

1. H = 0
2. H = + أ / ب
3. H = - أ / ب

وبعبارة أخرى ، فإن مواقف التوازن هي ثلاثة ، وليست واحدة. طباعة دقيقة: أبسطها كثيرًا هنا ، ولكن دون الإخلال بالمعنى.

هذا ليس واضحًا على الفور ، لكن الحل H = 0 غير مستقر. الموقف مشابه لمعادلة حركة كرة في وعاء بالشكل الموضح في الشكل. 2 - يشبه الجزء السفلي من زجاجة النبيذ. لديه أيضًا ثلاثة مواضع توازن ، واحد عند 0 واثنان عند ± x ₀ . ولكن من الواضح أن الموضع عند 0 غير مستقر - أي دفع سيؤدي إلى انحراف الكرة الحمراء بعيدًا عن x = 0 ، وهو تغيير جوهري في الموقف. على العكس من ذلك ، يكون التوازن عند x = x ₀ مستقرًا ، نظرًا لأن أي دفع سيؤدي إلى تذبذب الكرة الخضراء بسعة صغيرة حول النقطة x = x ₀ - ليس مثل هذا التغيير الجذري. وينطبق الشيء نفسه على الكرة الخضراء الفاتحة عند x = -x ₀ . وبالمثل ، على الرغم من أن H = 0 سيكون الحل لمعادلة حقل هيجز ، إلا أن تاريخ كوننا تبين أنه معقد بما يكفي لضمان أن حقل هيجز يجب أن يُركل بشكل صحيح ، لذلك لا يمكنه البقاء في هذا الموضع. بدلاً من ذلك ، كان حقل هيجز في حل بقيمة غير صفرية وفي وضع مستقر.



لعقود ، وبفضل مزيج من التجارب والنظرية ، كنا نعلم أن قيمة مجال هيجز (الذي يُسمى تقليديًا "v") هو 246 GeV. هذا يعطينا فكرة عن هذه الثوابت أ و ب:

أ = ف ب = (246 ج.ف) ب

وبالتالي ، يمكننا تحديد a من خلال b ، ويمكننا إعادة كتابة معادلة الحركة Higgs:

$$

$$d ^ 2H / dt ^ 2 - c ^ 2 d ^ 2H / dx ^ 2 = - b ^ 2 H (H ^ 2 - v ^ 2)$$

لكن هذا لا يعطينا فكرة عن نفسها. في المقالة القادمة سوف نتعلم المزيد عنه.

الآن ، على الرغم من أنني قد أعددت كل شيء بحيث يمكن أن تكون H مساوية لـ v أو –v ، لا يهم ما إذا كان حقل Higgs موجبًا أم سلبيًا (في الواقع ، هناك المزيد من الاحتمالات ، انظر أدناه) ؛ العالم سوف يتغير تمامًا ، بنفس الفيزياء ، حيث لا شيء يعتمد على علامة H. لا يصبح واضحا على الفور ، لكنه كذلك ؛ تلميح واحد - أينما وجدت H في المعادلات التي أصفها أو في وصف كيفية عمل حقل Higgs ، يظهر H ^{2 في} كل مكان ، وليس فقط H - و H ² لا يعتمد على H = v أو H = -v . [طباعة صغيرة: في الواقع ، H هو حقل معقد ، مع الأجزاء الحقيقية والخيالية ، لذلك يمكن أن يكون H مساوياً لـ v ضرب أي عدد مركب z يكون | z ​​| = 1 له ؛ وفي الواقع ، H * H = | H | ² ، لكنها لا تعتمد على z. وحتى هذا ليس كل شيء! ولكن يكفي هذا اليوم.]

إذا وجدت طريقة (على سبيل المثال ، عن طريق اصطدام البروتونات مع بعضها البعض في مصادم هادرون الكبير) لدفع أو إحداث اضطراب بطريقة ما في حقل هيجز ، فسوف تتأرجح وتتأرجح - أي أن الموجات تظهر في الشكل

$$

$$H = v + A cos [2 \ pi (\ nu t - x / \ lambda)]$$

حيث A هي اتساع الموجة ، ν و λ هي التردد وطول الموجة ، والعلاقة بين ν و λ تعتمد على الشكل الدقيق لمعادلة الحركة ، على وجه الخصوص ، على b و v. بما أن مجال هيجز هو كمومي ، فسيتم قياس اتساع هذه الموجات ، وحجم هذه الموجات هو ما نسميه جسيم هيجز. في المرة القادمة سننظر في خصائص هذه الجسيمات.