مرحبًا ، اسمي ألكسندر ، وأنا فيزيائي. من الخارج ، قد يبدو هذا بمثابة حكم ، ولكنه في الواقع كذلك. اتضح أنني أقوم بأبحاث أساسية في الفيزياء ، أي دراسة الجسيمات المشحونة المتسارعة: البروتونات وكل تلك الأكبر هي أيونات إيجابية ، أي. في الدراسات ، لا أستخدم مسرعات كبيرة مثل LHCs ، لكنني ألتقط الرقاقة باستخدام الليزر ، ويخرج زخم البروتون من الرقاقة.

الآن بضع كلمات عني. تخرجت من كلية ITOO للضوئيات والمعلوماتية البصرية في سانت بطرسبرغ ، ثم ذهبت إلى القضاء في جامعة آلتو (هذا في فنلندا) في اتجاه التكنولوجيا الدقيقة والنانوية ، ثم بصقت على كل هذه الأشياء الصغيرة ، المجاهر ، وخاصة في غرفة نظيفة. وذهبت إلى العلوم الأساسية باستخدام أشعة الليزر الكبيرة. أعمل الآن في كلية الدراسات العليا في جنوب غرب السويد في مدينة لوند في الجامعة التي تحمل الاسم نفسه. هذا عن مسافة مدفع من كوبنهاغن.

كما تسارع ، طار ذلك

إن مسرعات الجسيمات المشحونة نفسها ليست فكرة جديدة ، ولكن الطريقة التي أقوم بها بتسريعها جديدة نسبيًا ، في نفس عمري تقريبًا. يسمح لك بتقليل حجم المسرع وتكلفته بشكل كبير ، بما في ذلك تكلفة العمل والصيانة. يمكن تقدير الفرق بين النوعين في الصورة أدناه.

على اليسار يوجد مسرع خطي إلكتروستاتيكي (مفكك قليلاً) ؛ إلى اليمين صانع فويل لفتحاتي الصغير ولكنه فخور

دعونا نقارن هذين النمطين من العبقرية الجسدية القاتمة بمزيد من التفصيل. انظر إلى المعجل الأيسر واليمين ، ثم مرة أخرى إلى اليسار ومرة أخرى إلى اليمين: نعم ، خاصتي على حصان (مزحة - تعليق المؤلف). في الواقع ، لا يستغرق قطري سوى متر واحد ، ويتم تسريع البروتونات نفسها من قطعة من الرقاقة. يقع حاملها بالضبط في منتصف الدائرة ، مرتديًا تنورة نحاسية جميلة. إنها أبسط بكثير وأكثر إحكاما من العينة اليسرى ، والتي هي بحجم الحافلة بالإضافة إلى أنها مليئة بالغاز الخانق. لذا ، بعد أن أكدت نفسها في الكثير (غالبًا ما يحدث في الفيزياء أنه كلما كان أصغر كلما كان ذلك أفضل) ، يمكن للمرء أن يتحول إلى فيزياء عملية التسارع.

نظرًا لأننا نقوم بتسريع الجزيئات المشحونة ، فمن المنطقي جدًا القيام بذلك مع المجال الكهربائي. الحقل الذي سنميزه بالتوتر. بالنسبة لأولئك الذين ذهبوا إلى الأمام والخلف بعد المدرسة ، دعوني أذكركم: قوة المجال الكهربائي هي كمية فيزيائية متجهة تميز المجال الكهربائي في نقطة معينة وتساوي عدديًا نسبة القوة التي تعمل على شحنة نقطة ثابتة توضع في نقطة معينة في المجال حجم هذه الشحنة (لصق نسخة قذرة من ويكيبيديا). له أبعاد V / m. بالعودة إلى المقارنة ، يسرع المسرّع على اليسار البروتونات إلى 4 MeV (Megaelectron-volts) ، أي 2.77 * 10 ⁷ m / s أو 9.2٪ من سرعة الضوء. بما أن شحنة البروتون 1 ، وطول المسرع مترين ، فإن شدة المجال ستكون 2 MV / m. هنا افترضنا أن المجال موجه في جميع الأماكن في اتجاه واحد ، وبشكل عام ، كان قريبًا جدًا من الحقيقة. يحتوي المعجل الأنيق على قوة مجال بترتيب عدة تلفزيونات / م ، أي حوالي مليون مرة أكثر. ومع ذلك ، تجدر الإشارة إلى أن طوله ليس سوى بضع ميكرونات.

لذا ، عند هذه النقطة ، اكتشفنا أن مجاله أكثر حدة. حان الوقت للانتقال إلى الآليات المادية والهندسية التي يخلقها هذا المجال. في حالة المسرِّع التقليدي ، هناك صفحتان معدنيتان ، إحداهما سالبة ، والثانية بأي حال من الأحوال. تذكر تجربة المدرسة حول فرك عصا الإيبونيت بقطعة من الصوف. هنا المبدأ هو نفسه تمامًا ، لكن التنفيذ أكثر تعقيدًا. إذا قمت بتسريع البروتونات من الرقاقة ، يتم إنشاء المجال بواسطة الإلكترونات ، وتنتقل الإلكترونات من البلازما الساخنة ، ويتم الحصول على البلازما وتسخينها بواسطة الليزر ، وكل هذا هو بقية المنصب.

هل تريدني أن أضربه ويحول اللون الأرجواني إلى بقعة؟

إذا ضربت بقوة كافية ، يمكنك أن ترى العديد من الظواهر الفيزيائية الرائعة. هذه هي الطريقة التي حصل بها شباب هارفارد على الهيدروجين المعدني ، ثم فقدوه.

في حالتي ، ألتقط الرقاقة بالليزر. سأصفه بمزيد من التفصيل بعد شرح الفيزياء غير التافهة لعمليات الحصول على مادة كثيفة دافئة ، وهو بالضبط اسم البلازما من الناحية العلمية ، وهو المسؤول عن انتصار تسارع بروتوناتي. والآن ، أول شيء أولاً.

يولد الليزر نبضات بطول موجة 800 نانومتر و 35 fs لمدة ( ^10-15 ثانية) ، أي أن طول النبضة الفعلي في الفراغ هو حوالي 10 ميكرومتر. يتم دفع حوالي 2 J من الطاقة في هذا الدافع ، وهذا كثير. إذا أخذنا هذا الدافع وقمنا بتركيزه على ورق في بقعة دائرية أنيقة بقطر 5 ميكرون ، فستكون الكثافة في حدود 10 ²⁰ واط / سم ² . هذا غير لائق كثيرًا. مرة أخرى القليل من المقارنات: يمكن قطع الفولاذ بسهولة بكثافة 10 ⁸ واط / سم ² (أو نحو ذلك).

في الواقع ، بسبب ميزات التصميم الخاصة بمكبر الصوت ، فإن نبض الليزر لديه قاعدة سابقة تدوم حوالي 500 ps ، وهذه القاعدة تساعد بشكل كبير على تسريع البروتونات بشكل جيد.

أيوني - يعني مسلح

تذكر ما يحدث للضوء عندما يدخل مادة. يجب الحفاظ على الطاقة ، مما يعني أنه لا يوجد سوى ثلاثة أنواع من الأحداث: الانعكاس والانتقال والامتصاص. في الحياة القاسية ، كل ما سبق موجود في وقت واحد. في المرحلة المبكرة ، نحن مهتمون بالاستيعاب.

لذلك ، لدينا قاعدة ، والتي نركز عليها أيضًا بشكل مثالي على قطعة من الرقاقة ، ويتم امتصاصها تمامًا هناك. من أجل عدم الخوض في تعقيد فيزياء الحالة الصلبة ، فإننا نعتبر امتصاص ذرة قائمة بذاتها. من ميكانيكا الكم ، نعلم أنه لا يمكن امتصاص سوى الفوتون ، الذي تساوي طاقته تمامًا طاقة انتقال الإلكترون من حالة إلى أخرى. إذا كانت طاقة الفوتون أكبر من طاقة التأين (أي إرسال إلكترون من عش الوالدين إلى رحلة مجانية) ، فسيذهب الفائض إلى الطاقة الحركية للإلكترون ، كل شيء بسيط. في حالتنا ، الفوتونات ذات الطول الموجي 800 نانومتر ليس لديها طاقة كافية (هذه هي طاقة الفوتون الواحد ، وليس النبض كله!) لتأين الهدف ، ولكن هنا تأتي الفيزياء لمساعدتنا. تذكر ، لقد ذكرت شدة إشعاع أكبر؟ إذا كنا لا نزال نتذكر ، في الملحق ، أن الضوء يمكن تمثيله على أنه تدفق الفوتون ، وأن الشدة تتناسب معه مباشرة ، فعندئذٍ يتبين أن تدفق الفوتون كبير جدًا. وإذا كان التدفق كبيرًا جدًا ، فمن المحتمل أن تصل العديد من الفوتونات في نفس المكان وفي نفس الوقت ، وعندما يتم امتصاص طاقتها فإنها ستضاف ، وسيظل التأين يحدث. من الغريب أن هذه الظاهرة تسمى تأين متعدد الفوتونات ، ونحن نستخدمها بانتظام.

في الوقت الحالي ، لدينا تمزق الإلكترونات بنجاح ، مما يعني أن النبض الرئيسي يصل إلى البلازما النهائية ويبدأ في تسخينها.

أساسيات فيزياء البلازما (لم تأت بنكتة ، آه)

قبل التسخين ، يستحق الحديث قليلاً عن البلازما كحالة للمادة. البلازما ، مثل الغاز ، فقط الإلكترونات منفصلة ، والنويات منفصلة. سنعتبر البلازما غازًا مثاليًا تقريبًا ، ولكنها تتكون من إلكترونات.

ستكون الخاصية الرئيسية للبلازما هي كثافتها (عدد الإلكترونات لكل وحدة حجم) ، وسيتم الإشارة إلى هذه القيمة بـ $ n_e $ (لا يجب الخلط بينها وبين مؤشر الانكسار!) ، ودرجة حرارة هذه الإلكترونات ، أي متوسط سرعتها. يتم وصف هذا من خلال توزيع Boltzmann بنفس الطريقة كما في دورة الفيزياء المدرسية:

$$ display $$ \ frac {m_e v ^ 2} {2} = \ frac {1} {2} k_B T_e، $$ display $$

حيث يتبع بسهولة

$$ display $$ \ langle v \ rangle = \ sqrt [] {k_B T_e / m_e} ، $$ display $$

أين

$ مضمنة $ k_B $ مضمنة $ - ثابت بولتزمان

$ مضمنة $ T_e $ مضمنة $ هي درجة حرارة الإلكترون

$ مضمنة $ m_e $ مضمنة $ هي كتلة الإلكترون. نعم ، لقد نظرنا هنا في حالة أحادية البعد ، لكننا في الحقيقة لا نحتاج إلى المزيد لوصف عملياتنا ، في الواقع.

الآن نقوم بتطبيق مجال كهربائي على البلازما الموصوفة بالفعل. دعني أذكرك أن البلازما تتكون من جسيمات مشحونة ، مما يعني أنه عند كثافة معينة على مسافة معينة من المكان الذي طبقنا فيه المجال ، ستحجب الإلكترونات (درع) المصدر (مثل حشد من Matrosovs الصغير - ملاحظة المؤلف). والمسافة اللازمة لذلك تسمى طول ديبي وتعطى بالمعادلة

$$ display $$ \ lambda_D = \ sqrt [] {\ frac {\ epsilon_0 k_B T_e} {q ^ 2_e n_e}}. $$ display $$

هنا

$ مضمنة $ q_e $ مضمنة $ من الواضح أن شحنة الإلكترون و

$ inline $ \ epsilon_0 $ مضمنة $ - ثابت العزل الكهربائي للفراغ ، مثل هذا الثابت الأساسي. نقوم بتحليل هذه الصيغة قليلاً لرؤية الفيزياء البسيطة للعملية. من خلال زيادة كثافة الإلكترونات ، نقوم بتقليل متوسط المسافة بينهما ، ونتيجة لذلك ، للحصول على مسافة أصغر ، نجمع ما يكفي من الإلكترونات لحماية مجالنا تمامًا. من ناحية أخرى ، كلما ارتفعت درجة الحرارة ، زاد متوسط المسافة بين الإلكترونات.

نظرًا لتأثير الفحص ومتوسط درجة حرارة الإلكترونات المحدد جيدًا (اعتمادًا على درجة الحرارة) ، لا تتفاعل البلازما على الفور مع مجال يصل فجأة. من المنطقي أن نفترض أن وقت الاستجابة مرتبط بطول ديباي وسرعة الإلكترون. التشبيه الجيد هو إلقاء حجر على بحيرة. بالمقارنة مع البحيرة بأكملها ، يعمل الحجر على سطح الماء بشكل نقطي. يتغير جزء من الماء على الفور (هذا هو المكان الذي يتدفق فيه) ، ثم تبدأ الأمواج في الانتشار عبر سطح الماء. في حالة البلازما ، يكون المجال الكهربائي الذي يظهر فجأة هو الحجر. يتم تحديد حجم العمود بواسطة طول الشاشة (لا يعمل الحقل بعده) ، ويعتمد انتشار الموجات على مدى قرب الإلكترونات من بعضها البعض. يمكننا تقديم خاصية مثل وقت استجابة البلازما:

$ inline $ t_D = \ lambda_D / v $ inline $ . بشكل عام ، يوضح لنا الوقت الذي ستصل خلاله المعلومات حول التغيير في المجال التطبيقي إلى تلك الإلكترونات التي لم ترها كما هي.

بما أننا فيزيائيون ، فإننا لا نحب الوقت حقًا. إنه أكثر ملاءمة للعمل مع الترددات ، لذلك نقدم مفهوم التردد الطبيعي للبلازما. ستوضح لنا هذه القيمة عدد المرات التي يمكننا فيها تغيير المجال بحيث يكون للتراكم الكامل للإلكترونات ، الذي نسميه بفخر البلازما ، وقتًا للاستجابة لهذه التغييرات. حسنًا ، ما الذي يمكن أن يكون أسهل؟ اقسم الوحدة على وقت الاستجابة ، وهنا - التردد:

$$ display $$ \ omega_p = \ frac {1} {t_D} = \ sqrt [] {\ frac {q ^ 2_e n_e} {\ epsilon_0 m_e}}. $$ display $$

من السهل أن نرى أن التواتر الذاتي لتذبذبات البلازما يعتمد على كثافة الإلكترونات. كلما زاد عدد الإلكترونات ، زاد التردد. يمكنك رسم تشابه آخر ، ولكن هذه المرة مع بندول الربيع. تخبرنا كثافة الإلكترونات العالية أنها أقرب إلى بعضها البعض ، مما يعني أنها تتفاعل بقوة أكبر. نفترض أن تفاعلهم في نسبة مباشرة مرتبط بمرونة الربيع في البندول. وكلما زادت المرونة ، زاد تردد التذبذب.

يحدد التردد الطبيعي للبلازما أيضًا مؤشر الانكسار. لنكون صادقين ، نكتب معادلة الموجة للحركة الجماعية للإلكترونات في البلازما ، ثم نفترض تغييرات صغيرة في كثافة الإلكترونات (لن نقوم بذلك هنا لأنها مملة) ، ثم نضع مؤشر الانكسار على النحو التالي:

$$ display $$ \ eta = \ sqrt [] {1- \ frac {\ omega ^ 2_p} {\ omega ^ 2_0}}. $$ display $$

هنا

$ inline $ \ omega_0 $ مضمنة $ هو التردد الدائري للمجال الكهربائي المطبق. هي في راد / ثانية وليس في هرتز!

نحن ننظر بعناية إلى هذا التعبير. بصفتي فيزيائي تجريبي ، لا أشرب الأرواح بأعداد حقيقية ، لكنني أحاول تجاهل الأرواح المعقدة ، وخاصة مؤشر الانكسار المعقد. حسنًا ، كيف يمكن للضوء أن ينتشر في النهاية بشكل أبطأ من المرات في الفراغ؟ هذا نوع من الهراء! ليس حقًا ، ولكن أكثر من ذلك في وقت آخر. إذا

$ inline $ \ omega_0> \ omega_p $ مضمنة $ ، فإن التعبير له معنى حقيقي ، وينتشر مجال كهربائي متناوب داخل بلازما. الجميع سعداء ، وسنسمي هذه البلازما بكثافة غير كافية. ومع ذلك ، إذا

$ inline $ \ omega_0 <\ omega_p $ مضمنة $ ، يصبح مؤشر الانكسار ليس معقدًا فحسب ، بل يتخيل تمامًا. في هذه الحالة (وليس فقط لأنني أردت ذلك) لن تنتشر الموجة هناك على الإطلاق ، ولكنها ستنعكس على الفور دون خسارة. هذه بلازما كثيفة للغاية. بالمناسبة ظاهرة باردة جدا. يطلق عليه مرآة البلازما.

وكحلوى

$ inline $ \ omega_0 = \ omega_p $ مضمنة $ . هذه بلازما ذات كثافة حرجة. في هذه الحالة ، يبدأ في الدخول في الرنين مع تأثير كهربائي (يتم توفيره من قبلنا). في مثل هذه الحالة الخاصة ، يمكنك حتى تقديم مفهوم الكثافة الحرجة وتعريفها على النحو التالي:

$$ display $$ n_c = \ frac {\ epsilon_0 m_e \ omega ^ 2_0} {q ^ 2_e}. $$ display $$

بطبيعة الحال ، تختلف الكثافة الحرجة لكل تردد في مجال التأثير.

صدمة! تسخين البلازما! للقيام بذلك ، فقط ...

في حالتنا ، سنركز فقط على آلية تسخين واحدة ، والتي تسود في التجربة.

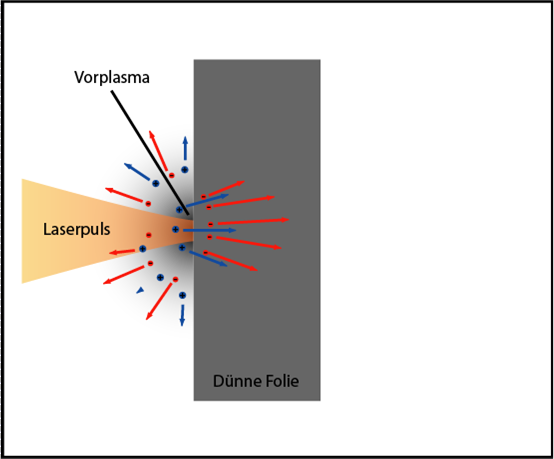
بادئ ذي بدء ، دع البلازما التي شكلناها بالعامود لها تدرج كثافة سلس ، في هذه الحالة لدينا تدفئة من خلال امتصاص الرنين. توضيح هذا في الصورة أدناه.

توضيح عملية امتصاص الرنين: أ) توزيع كثافة الإلكترون بالقرب من مقدمة الهدف. ب) انكسار حزمة الليزر في البلازما بتدرج الكثافة ؛ ج) المجال الكهربائي في البلازما

لذا ، يضيء الليزر على بلازمانا بزاوية ، حسنًا ، دعها تكون 45 درجة ، وفي نفس الوقت تكون مستقطبة في مستوى الورود. يشار إلى الاستقطاب بواسطة الأسهم الحمراء في الشكل. تتميز بلازمانا بتدرج الكثافة ، مما يعني أن مؤشر الانكسار يتغير باستمرار (هنا ينمو). في مرحلة ما ، سيحدث أن تصبح طبقة بلازما معينة لليزر لدينا "دورانية" وتعكس ، أي أنها تنتشر لبعض الوقت بالتوازي مع الطبقة الحرجة. من المهم أن نلاحظ أنها ستدور قبل أن تصل إلى طبقة الكثافة الحرجة ، حيث أطلقناها بزاوية على وضعها الطبيعي. تعطى كثافة البلازما التي يدور عندها شعاع الليزر بهذه المعادلة:

$$ display $$ n_t = n_c \ cos ^ 2 \ alpha، $$ display $$

أين

$ inline $ n_c $ مضمنة $ هي الكثافة الحرجة و

$ مضمنة $ \ alpha $ مضمنة $ - زاوية حدوث الضوء.

الآن يبدأ المرح. تذكر أن الضوء ليس مجرد تيار من الفوتونات ، ولكن أيضًا موجة كهرومغناطيسية ، أي أن زخمنا يحتوي على مجال كهربائي يتأرجح بشكل متناغم مع سعة كبيرة. عندما ينتشر الضوء بالتوازي مع الطبقة الحرجة ، تتشكل موجة دائمة ، والتي لا تتغير بمرور الوقت (بطبيعة الحال ، طالما أن نبض الليزر في مكانه). في الواقع ، يخترق مجال هذه الموجة أبعد من طبقة البلازما حيث تحول الضوء ، ويصل إلى الطبقة الحرجة. دعني أذكرك بأن تواتر تذبذبات البلازما في الطبقة الحرجة هو نفس تردد إشعاع الليزر ، مما يعني أن الرنين يحدث. عندما يتوقف الليزر عن اللمعان ، يتم توزيع الطاقة التي ينقلها إلى الإلكترونات في الطبقة الحرجة من خلال التأثيرات على الإلكترونات الأخرى ، مما يعني أن البلازما ساخنة.

إذن ، أين هو التسارع؟

الآن بعد أن قمنا بتسخين الإلكترونات في بئر البلازما ، ولم يعد الليزر يلمع ، يمكننا أن نقول كيف يتم تسريع البروتونات. للقيام بذلك ، انظر إلى الصور أدناه. حتى هذه اللحظة ، لم أقل أبدًا من أين تأتي البروتونات. بطبيعة الحال ، لا تظهر من نوى مادة الرقائق. نظرًا لأننا لسنا أنيقين جدًا ولا نرتدي قفازات (تتعرق اليدين بشدة) ، فإن الماء والهيدروكربونات موجودة على سطح الرقاقة. الهيدروجين المتأين هو مصدرنا لا يقدر بثمن للبروتونات. تم الفحص: إذا قمت بإزالة التلوث ، فلن تكون هناك بروتونات.

	تشكيل البلازما بقاعدة ، أي تأين الجزء الأمامي من الهدف. كهدف ، عادة ما يتم استخدام رقائق بسمك 0.4-12 ميكرون.
	هنا ، يتفاعل الجزء الرئيسي من النبض مع البلازما الناتجة ويسخنها. ارتفعت درجة حرارة بعض الإلكترونات بشكل جيد لدرجة أنها تطير من خلف الهدف.
	عندما تطير الكثير من الإلكترونات ، فإن الشحنة الموجبة المتبقية في الرقاقة تسحبها للخلف. في البلازما ، تسخن مرة أخرى وتطير. لبعض الوقت ، يتم إنشاء توازن ديناميكي. يتم توجيه المجال الكهربائي بشكل عمودي على الهدف
	يفصل هذا المجال الكهربائي للغاية البروتونات والأيونات الأخرى (اعتمادًا على ما هو موجود على الإطلاق) من السطح الخلفي للهدف ، ثم يسرعها. في الوقت الذي تتسارع فيه الأيونات ، تنهار سحابة الإلكترونات بالفعل ، وتبدأ كل الجسيمات في التحليق معًا أكثر. ثم نبدأ في الاعتقاد بأنهم لم يعودوا يتفاعلون بعد الآن.

فرق تسد

في الوقت الحالي ، هذا هو الموقف: لم يكن الليزر يلمع لفترة طويلة ، هناك ثقب في الرقاقة ، والبروتونات ذات الإلكترونات ودية الطيران من الهدف عادة إلى سطحه الخلفي. لا نحتاج إلى إلكترونات على الإطلاق ، لهذا السبب يأتي المغناطيس لمساعدتنا. عندما تطير حزمة من الجسيمات المشحونة عبر مجال مغناطيسي ، تنحرف قوى لورنتز لكل جسيم بما يتناسب مع سرعته وشحنه. تبعا لذلك ، سوف تنحرف البروتونات والإلكترونات في اتجاهات مختلفة ، ونحن ببساطة لن ننظر في اتجاه الإلكترونات. بالمناسبة ، كلما زادت طاقة البروتون (أي سرعته) ، كلما قل انحرافه.هذا يعني أنه بوضع شاشة حساسة للبروتونات ، يمكننا أن نرى طاقات البروتونات المتسارعة. المزيد من المقارنات في الأرقام: مغناطيس يقف معنا بشكل دائم ويخلق مجالًا يبلغ حوالي 0.75 طنًا ؛ المجال المغناطيسي في أجهزة التصوير بالرنين المغناطيسي هو 1.5 - 3 T.

بالإضافة إلى ذلك ، يمكننا أن نرى الملف الشخصي لحزمة من البروتونات الطائرة. بالمناسبة ، إنها مستديرة. وإذا استطعنا أيضًا قياس طاقة البروتون في كل جزء من الشعاع ، فيمكننا استعادة شكل سحابة الإلكترون بشكل فريد ، مما أدى إلى تسريع بروتوناتنا.

بدلا من الاستنتاج

قد يطرح سؤال عادل ، لماذا كل هذا ضروري. جوابي المفضل هو هكذا هذا علم أساسي ، ومحاولة العثور على تطبيقاته المؤقتة لا طائل من ورائها. ربما في بعض السنوات سيجد تطبيقه في علاج السرطان أو الاندماج النووي الحراري ، لكن المهمة الرئيسية الآن هي معرفة شيء جديد عن العالم من حولنا ، تمامًا مثل ذلك ، لأنه مثير للاهتمام.

لأولئك الذين لديهم فضول خاص حول الليزر نفسه وجهازه

كما وعدت ، سأتحدث هنا عن الليزر ، بمساعدة العلوم. لقد ذكرت بالفعل بعض خصائص الليزر الخاص بنا ، لكنني لم أتحدث عن معدل تكرار النبض. حوالي 80 ميجا هرتز. يتم تحديد هذا التردد فقط من خلال طول الرنان وعكس الوقت الذي يتمكن فيه الضوء من التحليق ذهابًا وإيابًا عبر الرنان. بالنظر إلى المستقبل ، سأقول أنه من غير العملي تضخيم النبضات عند هذا التردد ، إنه أمر صعب للغاية من وجهة نظر هندسية ، ولا يمكنك توفير الكهرباء.

لن أخوض في نظرية الليزر بشكل خاص. تم تحديد أساسيات مصدر إشعاع الليزر بشكل مثالي في مقالة ويكيبيديا حول الانبعاث المحفز. إذا حاولت أن تكون قصيرًا جدًا ، فستكون هناك حاجة إلى ثلاثة مكونات لإشعاع الليزر: الوسط النشط (الفوتونات تطير منه أيضًا) ، الضخ (يحافظ على الوسط النشط في الحالة التي يوجد فيها ذرات أكثر إثارة يمكن أن تنبعث) ، وأيضًا مرنان ( يضمن أن الفوتونات تنسخ بعضها البعض خلال تمريرات متعددة من خلال الوسط النشط). إذا جمعت كل المكونات معًا وصليت ، سيبدأ الليزر في التألق ، ولكن بشكل مستمر. إذا حاولت مرة أخرى ، يمكنك جعله يولد نبضات ، بما في ذلك تلك قصيرة مثل التثبيت. بالنسبة للفضول ،طريقة توليد نبضات الفيمتو ثانية تسمى قفل الوضع السلبي. والآن سمة صغيرة من البقول قصيرة جدا. غالبًا ما يُعتقد أن الليزر يضيء في نفس الطول الموجي ، وفي الوضع المستمر ، وكذلك في النبضات الطويلة ، يمكن أن يسمى هذا صحيحًا. في الواقع ، نظرًا لعدد من العمليات الفيزيائية المعقدة ، والتي لن نناقشها بالتأكيد هنا ، يرتبط الشكل الزمني للنبض وطيفه بتحويل فورييه. أي أنه كلما كان النبض أقصر ، كان طيفه أوسع.يرتبط الشكل الزمني للنبض وطيفه بتحويل فورييه. أي أنه كلما كان النبض أقصر ، كان طيفه أوسع.يرتبط الشكل الزمني للنبض وطيفه بتحويل فورييه. أي أنه كلما كان النبض أقصر ، كان طيفه أوسع.

لنفترض أننا أطلقنا مذبذبًا رئيسيًا ، لكن طاقة نبضاته هي عدة نيوجيرسي. تذكر ، في البداية قلت أن الطاقة في نبضة تصل إلى الهدف حوالي 2 جول؟ إذن ، هذا مليار مرة أكثر. وهذا يعني أن الزخم يحتاج إلى تعزيز ، وسنتحدث عن هذا بمزيد من التفصيل.

تتميز النبضات القصيرة عمومًا بقدرات ذروة كبيرة جدًا (تذكر ، هل تشارك الطاقة مع الوقت؟) ، وهذا له عدد من المضاعفات. إذا كانت الوسائط مضاءة بإشعاع بكثافة عالية (الطاقة لكل وحدة مساحة) ، فستحترق ، وإذا تم حرق الوسط النشط ، فلن يتم تضخيم أي شيء. هذا هو السبب في أننا نختار معدل التكرار 10 هرتز ونضخمهم فقط. نظرًا لوجود الكثير من المعدات وكلها تعمل على مثل هذا التردد ، فلدينا صندوق خاص يوزع هذه 10 هرتز على جميع المكواة ، ولكل جهاز يمكنك اختيار التأخير في استقبال الإشارة بدقة بضع بيكو ثانية.

هناك طريقتان للتعامل مع كثافة عالية. كما يمكنك التخمين بسهولة من تعريفها ، تحتاج إما إلى زيادة المساحة أو تقليل الطاقة. مع الأول ، كل شيء واضح للغاية ، ولكن الطريقة الثانية كانت طفرة في تكنولوجيا الليزر في القرن العشرين. إذا كان النبض قصيرًا جدًا في البداية ، فيمكن تمديده وتقويته ثم ضغطه مرة أخرى.

لفهم كيفية القيام بذلك ، ننتقل إلى أساسيات البصريات. بالنسبة لأطوال موجية مختلفة ، تختلف مؤشرات الانكسار في الوسط ، مما يعني (من خلال تعريف معامل الانكسار ، بالمناسبة) أنه مع زيادة معامل الانكسار ، تنخفض سرعة انتشار الضوء في الوسط. وهكذا أطلقنا دافعنا يوم الأربعاء ، ومر الجزء الأحمر من خلال المادة بشكل أسرع من المادة الزرقاء ، أي أن الدافع أصبح أطول ، وانخفضت ذروة قوته. مرحى ، الآن لا شيء يحترق! للحصول على معرفة أعمق في هذا المجال ، أوصي بـ googling والقراءة حول تضخيم النبضات المفرومة (المعروف أيضًا باسم تضخيم النبض Chirped أو CPA).

كل ما تبقى لنا هو زيادة الزخم والضغط والتركيز وإرساله لعمل ثقب في الرقاقة!

والآن بعض الصور مع التسميات التوضيحية.