كيف يعمل حقل هيجز: 3) كيف يظهر جسيم هيجز

كيف يعمل حقل هيجز:

1. الفكرة الرئيسية
2. لماذا متوسط ​​حقل هيجز غير صفري
3. كيف يظهر جسيم هيجز
4. لماذا يعد حقل هيجز ضروريًا

في مقال سابق ، وصفت كيف ولماذا لا يحتوي حقل هيجز على متوسط ​​قيمة صفر. الآن أريد أن أصف ما هو جسيم هيجز وكيف تنشأ كتلته من المعادلات.

أريد أن أذكرك أنه إذا لم يتم ذكر العكس ، فأنا أصف دائمًا أبسط شكل ممكن من المجال وجسيم هيجز - ما يسمى نموذج هيجز القياسي. الأشكال الأكثر تعقيدًا ممكنة أيضًا ؛ على سبيل المثال ، قد توجد عدة حقول هيجز في وقت واحد ، بدلاً من واحد. ربما سأصف حالة أكثر تعقيدًا في إحدى المقالات التالية.


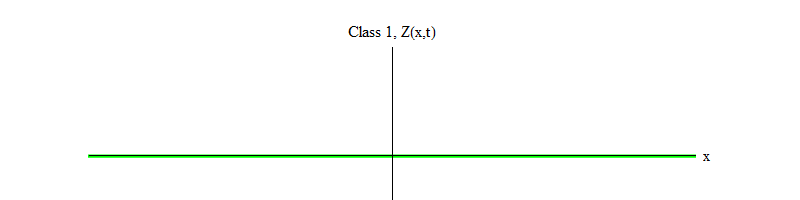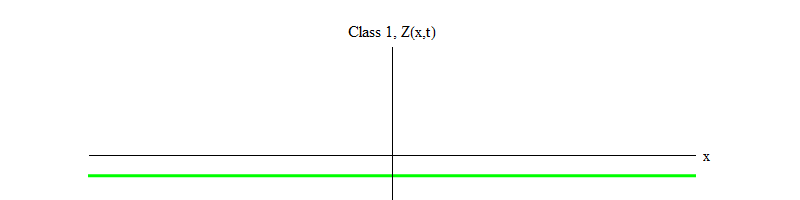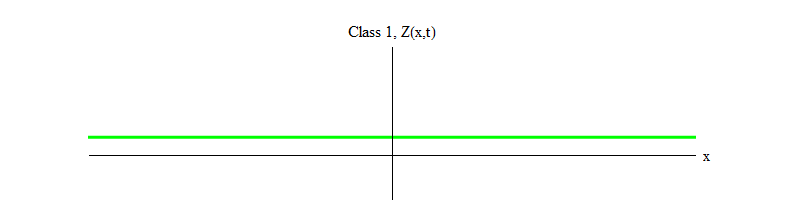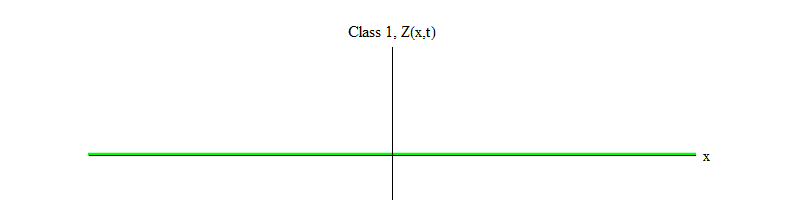التين. 1: يتغير حقل الفئة 1 في الوقت المناسب حول قيمة ثابتة Z (x، t) = 0

في المقالة الأخيرة ، لم أؤكد على هذه الحقيقة ، ولكن من بين المجالات الأولية التي اكتشفناها في الطبيعة ، فإن مجال هيجز فريد من نوعه. جميع الحقول ، باستثناء هيجز ، تستوفي معادلات الحركة للفئة 0 أو 1. في الواقع (على الرغم من أن هذا ليس هو الحال بالنسبة لجميع الحقول في الطبيعة) ، فإن جميع الحقول التي نعرفها تفي بمعادلات الفئة 1 تفعل ذلك لأن حقل هيجز غير صفري . إذا كانت صفرًا ، فستلبي جميعًا معادلات الفئة 0 (كما أوضحت في المقالة الأولى). بدلاً من ذلك ، يفي حقل هيجز بمعادلة يمكن أن تسمى معادلة الفئة -1.

بالنسبة للحقل Z (x، t) ، تبدو الفئات التي حددتها كما يلي:

$$

$$d ^ 2Z / dt ^ 2 - c ^ 2 d ^ 2Z / dx ^ 2 = - B ^ 2 Z \ quad [Class 1 - massive \؛ الجسيمات] \\ d ^ 2Z / dt ^ 2 - c ^ 2 d ^ 2Z / dx ^ 2 = 0 \ quad [Class 0 - massless \؛ الجسيمات] \\ d ^ 2Z / dt ^ 2 - c ^ 2 d ^ 2Z / dx ^ 2 = + B ^ 2 Z \ quad [Class -1 - unstable]$$

المعادلات تعني أن B ² > 0.


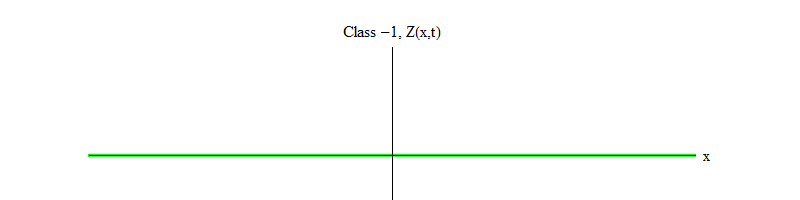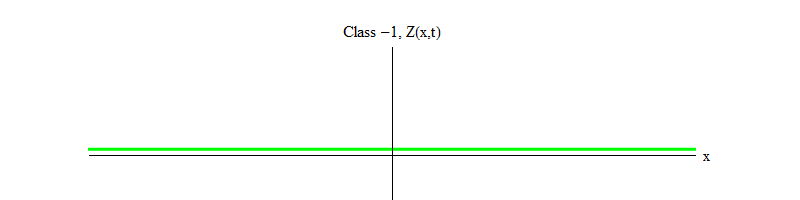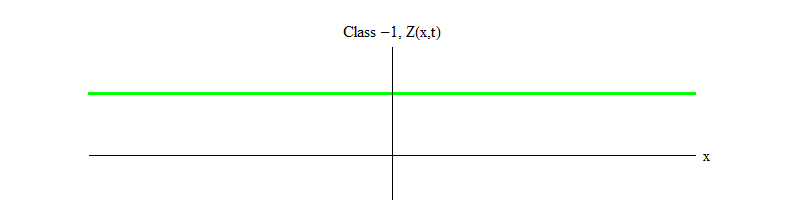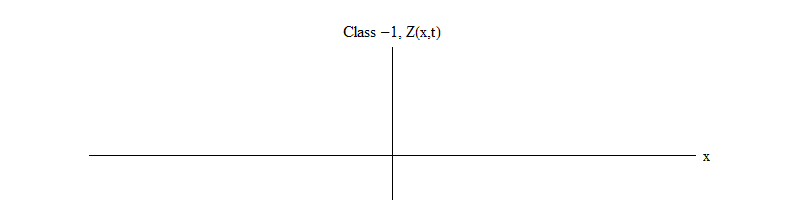التين. 2: حقل من الفئة -1 يترك التوازن غير المستقر Z (x، t) = 0.

علامة الطرح بين الفئة 1 والفئة -1 مهمة جدًا. في كلتا الحالتين ، تحتوي حلول المعادلات على Z (x، t) = 0 كواحدة من الحالات الخاصة ، ولكن بالنسبة للفئة 1 Z (x، t) = 0 مستقرة ، أي أن Z (x، t) يمكن أن تتقلب حول الصفر ؛ هذه موجات تتصرف بشكل لائق مع كمية ضخمة. والعكس صحيح ، الفئة -1 Z (x، t) = 0 غير مستقرة ، أي أن Z (x، t) لن تتقلب ، بل تنمو إلى المزيد والمزيد من القيم. إذا لم تقم بتغيير المعادلة ، فإن حجم المجال سيطير إلى ما لا نهاية. بتعبير أدق ، إذا كان حل معادلة الفئة 1 هو التذبذب Z ، كما في الشكل. 1 ، حل معادلة الفئة -1 هو نمو أسي لـ Z ، كما في الشكل. 2.

بالنسبة لحقل هيجز ، وأي حقل موجود في الطبيعة ، يتم تغيير معادلة الفئة -1 باستخدام المصطلحات التي تحد من النمو الأسي وتمنع المجال من الانتقال إلى ما لا نهاية. كما رأينا في المقالة السابقة ، يخضع حقل هيجز لمعادلة الحركة

$$

$$d ^ 2H / dt ^ 2 - c ^ 2 d ^ 2H / dx ^ 2 = - b ^ 2 H (H ^ 2 - v ^ 2) = + (bv) ^ 2 H - b ^ 2 H ^ 3$$

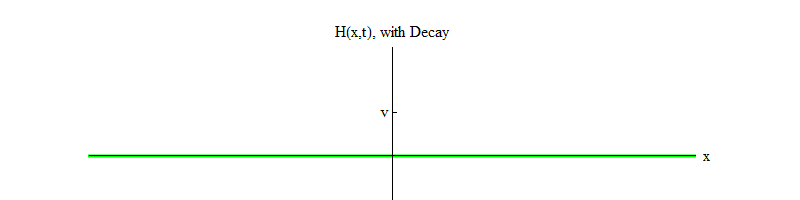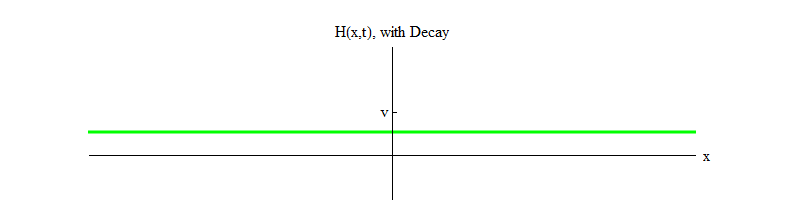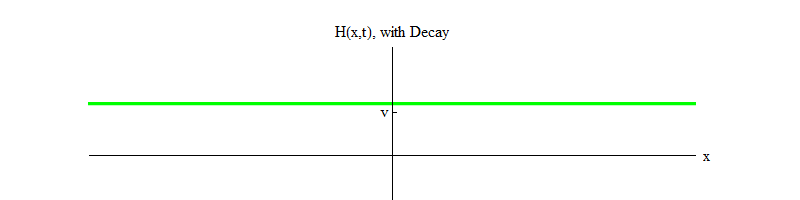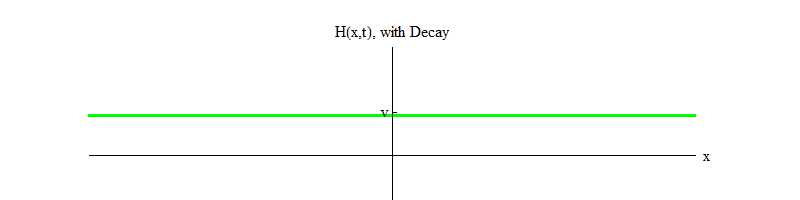
وهي تنتمي إلى الفئة -1 عندما تكون H تقريبًا صفرًا ، ولكنها تحتوي على عضو مهم في H ³ . هنا b عبارة عن رقم موجب ، و v هو موضع التوازن لـ H. تضمن هذه المعادلة أنه إذا بدأ الحقل H عند النقطة H = 0 وانتقل من موضع التوازن غير المستقر إلى الموجب H ، فسوف يتذبذب حول موضع التوازن المستقر في H = v (الشكل 3).


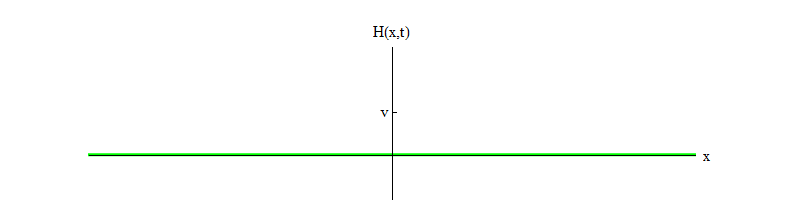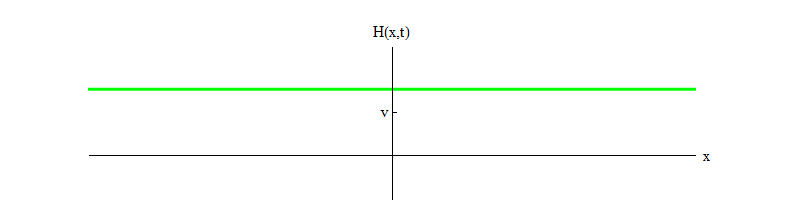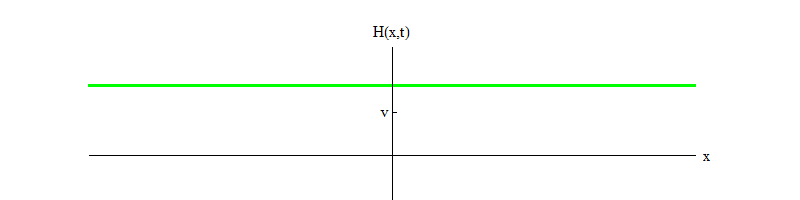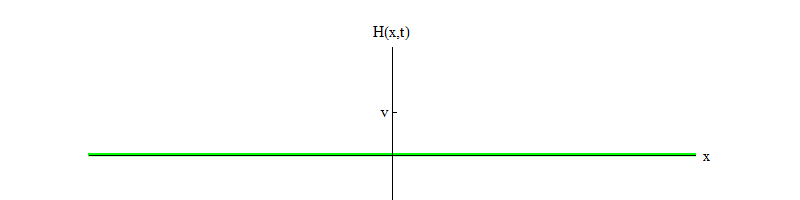التين. 3

بمرور الوقت ، سوف تتلاشى التذبذبات ، بسبب شروط معادلة الحركة ، التي حذفتها للإيجاز ؛ إنها تسمح بنقل جزء من طاقة التذبذبات في المجال H إلى موجات الحقول الأخرى (هذه هي نفس المصطلحات غير الخطية التي تسمح لجسيمات هيجز بالتحلل ). بمرور الوقت (الشكل 4) ، يهدأ الحقل H في الموضع H = v.


التين. 4

إذا كانت أي عملية فيزيائية تطرق الحقل من الموضع H = v في منطقة صغيرة من الفضاء ، فسوف ينبعث الحقل موجات من النموذج

$$

$$H = v + A cos [2 \ pi (\ nu t - x / \ lambda)]$$

حيث A هي اتساع الموجة ، ν و λ هي ترددها وطولها الموجي ، وتعتمد العلاقة بين ν و λ على الشكل الدقيق لمعادلة الحركة ، على وجه الخصوص ، على b و v. وستكون كمية هذه الموجات هي جسيمات هيجز. السؤال لكل مليون: ما هي كتلة جسيم هيجز؟ لحساب هذا ، نحتاج ، كما هو مطلوب دائمًا للجسيمات (تمثل كمية الموجة في المجالات النسبية) ، تحديد العلاقة بين التردد ν وطول الموجة λ لموجات المجال المقابل ، ثم ضرب النتيجة في ثابت Planck h للحصول على النسبة بين الطاقة والزخم الكمي لهذه الموجات ، والذي سيخبرنا عن كتلة الكم (أي الجسيمات).

نقوم بذلك فقط مع الحقل S (x ، t) المذكور في المقالة الأولى . نكتب نسخة منقولة من حقل هيجز ، معبرين عنها بـ H (x، t) = v + h (x، t) ، ونستبدلها في معادلة الحركة للمجال H. h (x، t) سأكتب بخط غامق لتمييزها من ثابت بلانك ح. في المثال الخاص بالحقل S الوارد في مقالة المراجعة ، تمت الإشارة إلى معادلة بسيطة للحركة ، لذلك لم يغير التحول كتلة الجسيم S. ولكن في هذه الحالة لم يحدث ذلك! معادلة حركة مجال هيجز أكثر تعقيدًا ، لذلك تختلف معادلة h تمامًا عن المعادلة الأصلية لـ H:

$$

$$d ^ 2 \ textbf {h} / dt ^ 2 - c ^ 2 d ^ 2 \ textbf {h} / dx ^ 2 = - b ^ 2 (v + \ textbf {h}) (2 v \ textbf {h} + \ textbf {h} ^ 2)$$

حيث استخدمت حقيقة أن v ثابت ومستقل عن المكان والزمان. ثم نتذكر أن كمية مجال هيجز لها سعة صغيرة ، لذلك ، عند دراسة جسيم هيجز الوحيد (وهو بالضبط ما نحتاجه لتحديد كتلته) ، يمكننا تجاهل جميع المصطلحات التي تتناسب مع h ² و h ³ :

$$

$$d ^ 2 \ textbf {h} / dt ^ 2 - c ^ 2 d ^ 2 \ textbf {h} / dx ^ 2 = - 2 b ^ 2 v ^ 2 \ textbf {h} + ...$$

حيث يتذكر "+ ..." إسقاط الأعضاء. لاحظ أن هذه المعادلة لـ h (x، t) تنتمي إلى الفئة 1 ، على الرغم من أننا بدأنا بمعادلة الفئة -1 لـ H (x، t) ؛ هذا لأن H (x، t) كان غير مستقر في منطقة H = 0 ، وكان h (x، t) مستقرًا في منطقة h = 0 ، حيث H = v. لذا يمكننا حساب الكتلة m _h لجزيء Higgs h باستخدام الشكل التالي من معادلة الفئة 1:

$$

$$m_h = \ sqrt2 (h / 2 \ pi) b v / c ^ 2$$

يشير h على الجانب الأيمن إلى ثابت Planck. إذا تبين أن الجسيم الشبيه بـ Higgs الذي تم العثور عليه مؤخرًا على LHC هو جسيم Higgs للنموذج القياسي ، فعندئذ لأول مرة يمكننا معرفة ما هو b (تذكر أن v كنا نعرف بالفعل منذ وقت طويل جدًا) ، وأخيرًا ، يمكننا معرفة القيمة a = b v.

• ت = 246 جيف ؛
• m _h ≈ 125 GeV / c² (إذا كان الجسيم الجديد Higgs)
• b ≈ 0.35 (2 π / h) (إذا كان الجسيم الجديد هو Higgs للنموذج القياسي)
• a = bv ≈ 87 GeV (2 π / h) (إذا كان الجسيم الجديد هو Higgs للنموذج القياسي)

حيث h ، مرة أخرى ، هو ثابت بلانك. ولم تكن الكميات الثلاث الأخيرة معروفة لنا حتى الاكتشاف الأخير لجسيم هيجز.

الآن ، إذا اتضح أن النموذج القياسي لا يتوافق مع الطبيعة (إذا كان بالإضافة إلى H (x ، t) ، فمن الضروري إضافة حقول إضافية إلى الحقول المعروفة لشرح خصائص الجسيمات المكتشفة حديثًا للكتلة 125 GeV / c²) ، فلنفترض أن هذا الجسيم هو واحد من عدة أنواع جسيمات هيجز - ثم علينا أن نتعامل مع هذا الوضع الصعب على المصادم LHC لبضع سنوات أخرى. يمكنك أن تتخيل العديد من الاحتمالات ، ولا معنى لشرحها لكم جميعًا ، لكني تقريبًا وصفت بعضها هنا ؛ وإذا كانت البيانات المستلمة في المصادم LHC ستظهر لنا اتجاهًا معينًا ، فسأشرح لك كل شيء بالتفصيل.