كتاب "ميكانيكا الكم. الحد الأدنى النظري "

الميكانيكا الكلاسيكية بديهية: يتم استخدامها يوميًا وبشكل متكرر من قبل الناس من أجل البقاء. ولكن حتى القرن العشرين ، لم يستخدم أحد ميكانيكا الكم. تصف أشياء صغيرة جدًا لدرجة أنها تسقط تمامًا من إدراك الحواس البشرية. الطريقة الوحيدة لفهم هذه النظرية ، للتمتع بجمالها ، هي منع حدسنا بالرياضيات المجردة.

يدعوك ليونارد ساسكيند - عالم أمريكي شهير - للذهاب في رحلة مثيرة إلى بلد ميكانيكا الكم. في الطريق ، ستحتاج إلى المعرفة الأساسية من دورة الفيزياء المدرسية ، بالإضافة إلى أساسيات التحليل الرياضي والجبر الخطي. تحتاج أيضًا إلى معرفة شيء عن القضايا التي تم تناولها في أول كتاب لـ Susskind بعنوان "الحد الأدنى النظري" - "كل ما تحتاج إلى معرفته عن الفيزياء الحديثة". ولكن لا خوف إذا تم نسيان هذه المعرفة إلى حد ما. سيذكر الكثير من المؤلف ويشرح على طول الطريق.

ميكانيكا الكم هي نظرية غير عادية: وفقًا لفرضياتها ، على سبيل المثال ، يمكننا معرفة كل شيء عن النظام ولا شيء عن أجزائه الفردية. جادل آينشتاين ونيلز بور الكثير حول هذا التناقض وغيرها. إذا لم تكن خائفًا من الصعوبات ، ولديك عقل استفساري ، وكفؤًا تقنيًا ، ومهتمًا بشدة بالفيزياء ، فستناشدك هذه الدورة من المحاضرات التي كتبها ليونارد ساسكيند. يركز الكتاب على المبادئ المنطقية لنظرية الكم ولا يهدف إلى تخفيف تناقض المنطق الكمي ، بل سحبه إلى النور ومحاولة التعامل مع القضايا الصعبة التي يثيرها.

نظرة عامة على وظيفة الموجة

في هذه المحاضرة سوف نستخدم لغة الدوال الموجية ، لذلك دعونا نقوم بمراجعة قصيرة للمواد قبل الغوص. ناقشنا في المحاضرة 5 الدوال الموجية للأجسام المجردة ، دون شرح كيفية ارتباطها بالموجات أو الدوال. قبل ملء هذه الفجوة ، أذكرك بما ناقشناه سابقًا.

بادئ ذي بدء ، نختار L يمكن ملاحظته مع القيم الذاتية l والمتجهات الذاتية | l〉. دع | Y〉 يكون ناقل دولة. نظرًا لأن المتجهات الذاتية للعامل Hermitian تشكل أساسًا متعامدًا كاملاً ، يمكن توسيع المتجه | Y in على هذا الأساس:

كما تتذكر من القسمين 5.1.2 و 5.1.3 ، تسمى الكميات Y (l) دالة الموجة للنظام. لكن لاحظ: يعتمد الشكل المحدد لـ Y (l) على L المحدد المحدد الذي اخترناه في الأصل. إذا اخترنا ملاحظة أخرى يمكن ملاحظتها ، فإن الدالة الموجية (إلى جانب المتجهات الأساسية والقيم الذاتية) ستكون مختلفة ، على الرغم من حقيقة أننا لا نزال نتحدث عن نفس الحالة. لذلك ، يجب أن نحجز أن Y (l) هي دالة الموجة المرتبطة بـ | Yñ. على وجه الدقة ، يجب أن نقول أن Y (l) هي دالة الموجة في الأساس L. إذا استخدمنا خصائص التعامد لهذا الأساس للمتجهات 〈li | lj〉 = dij ، فيمكن أيضًا تعريف الدالة الموجية في هذا الأساس باستخدام المنتجات الداخلية (أو الإسقاطات) لناقل الحالة | Y〉 على المتجهات الذاتية | l〉: Y (l ) = 〈L | Y〉

هناك طريقتان للتفكير في الدالة الموجية. بادئ ذي بدء ، هذه مجموعة من مكونات ناقل الحالة على أساس محدد. يمكن كتابة هذه المكونات في شكل ناقل عمود:



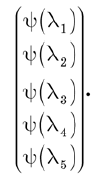
طريقة أخرى للتفكير في الدالة الموجية هي اعتبارها دالة لـ l. إذا قمت بتعيين أي قيمة صالحة لـ l ، فإن الدالة Y (l) تعطي رقمًا مركبًا. وبالتالي ، يمكننا القول أن Y (l) هي دالة ذات قيمة معقدة للمتغير المنفصل l. مع هذا الاعتبار ، تصبح العوامل الخطية عمليات تنطبق على الوظائف وتعطي وظائف جديدة.

وآخر تذكير آخر: احتمال أن تعطي التجربة النتيجة l تساوي P (l) = Y * (l) Y (l).

وظائف وناقلات

حتى الآن ، كان للأنظمة التي درسناها متجهات حالة ذات أبعاد محدودة. على سبيل المثال ، يتم وصف الدوران البسيط بمسافة حالة ثنائية الأبعاد. لهذا السبب ، لم يكن للملاحظات سوى عدد محدود من القيم التي يمكن ملاحظتها. ولكن هناك ملاحظات أكثر تعقيدًا يمكن أن يكون لها عدد لا نهائي من القيم. المثال هو جسيم. يمكن ملاحظة إحداثيات الجسيمات ، ولكن على عكس الدوران ، فإن الإحداثيات لها عدد لا نهائي من القيم المحتملة. على سبيل المثال ، يمكن أن يكون الجسيم المتحرك على طول المحور x في أي علامة مادة x. بمعنى آخر ، x متغير لانهائي مستمر. عندما تكون الأنظمة المرصودة مستمرة ، تصبح الدالة الموجية دالة كاملة للمتغير المستمر. لتطبيق ميكانيكا الكم على أنظمة من هذا النوع ، يجب علينا توسيع مفهوم المتجهات بحيث تشمل الوظائف فيه.

الوظائف هي الوظائف ، وناقلات المتجهات ؛ يبدو أنها كيانات مختلفة تمامًا ، فما معنى الدوافع؟ إذا كنت تفكر في المتجهات باعتبارها سهامًا في مساحة ثلاثية الأبعاد ، فبالتأكيد لا تختلف تمامًا عن الوظائف. ولكن إذا نظرت إلى المتجهات على نطاق أوسع ، كما هو الحال في الأشياء الرياضية التي ترضي بعض المسلمات ، فإن الوظائف تشكل في الواقع مساحة متجهة. غالبًا ما يطلق على مثل هذا الفضاء المتجه مساحة هيلبرت تكريمًا لعالم الرياضيات ديفيد هيلبرت.

خذ بعين الاعتبار مجموعة الوظائف المعقدة Y (x) لمتغير حقيقي x. بواسطة دالة معقدة ، أعني أنه لكل x يربط العدد المركب Y (x). المتغير المستقل x ، من ناحية أخرى ، هو متغير حقيقي عادي. يمكن أن يأخذ أي قيم حقيقية من –∞ إلى + ∞.

الآن نقول بالضبط ما نعنيه بالقول أن "الوظائف هي ناقلات". هذا ليس تشبيهًا أو تشبيهًا سطحيًا. تحت بعض القيود (التي سنعود إليها لاحقًا) ، تفي الدالات مثل Y (x) البديهيات الرياضية التي تحدد مساحة المتجه. ذكرنا بإيجاز هذه الفكرة في القسم 1.9.2 ، والآن نستخدمها بكامل قوتها. إذا نظرنا إلى الوراء في بديهيات مساحة ناقل معقدة (في القسم 1.9.1) ، نرى أن الوظائف المعقدة ترضيهم جميعًا.

1. مجموع أي وظيفتين دالة.
2. إضافة وظائف تبادلية.
3. إضافة وظائف هي جمعية.
4. هناك وظيفة صفرية فريدة بحيث يتم إضافتها إلى أي وظيفة عند إضافتها إلى أي وظيفة.
5. بالنسبة لأي دالة معينة Y (x) ، توجد دالة فريدة –Y (x) بحيث تكون Y (x) + (–Y (x)) = 0.
6. إن ضرب دالة بأي رقم مركب يعطي دالة وهو خطي.
7. لوحظ خاصية التوزيع ، مما يعني ذلك

z [Y (x) + j (x)] = zY (x) + zj (x) ،
[z + w] Y (x) = zY (x) + wY (x) ،

حيث z و w هي أرقام معقدة.

كل هذا يعني أنه يمكننا تحديد الدالة Y (x) مع متجه ket | Y〉 في مساحة المتجه المجردة. ليس من المستغرب أن نتمكن أيضًا من تحديد نواقل حمالة الصدر. يتم تحديد متجه حمالة الصدر 〈Y | المقابل لـ chum sal | Y〉 بوظيفة الاقتران المعقدة Y * (x).

لاستخدام هذه الفكرة بفعالية ، نحتاج إلى تعميم بعض الأشياء من مجموعة أدواتنا الرياضية. في المحاضرات السابقة ، كانت التسميات التي حددت وظائف الموجة أعضاء في مجموعة منفصلة محدودة ، على سبيل المثال ، القيم الذاتية لملاحظة معينة. لكن المتغير المستقل مستمر الآن. هذا يعني ، من بين أمور أخرى ، أنه لا يمكننا تلخيصه باستخدام مبالغ عادية. أعتقد أنك تعرف ماذا تفعل. فيما يلي بدائل موجهة نحو الوظيفة لمفاهيمنا الثلاثة لناقلات ، اثنان منها مألوفتان لك بالفعل.

• استبدال المبالغ بالتكاملات.
• يتم استبدال الاحتمالات بكثافات الاحتمال.
• يتم استبدال رمز دلتا كرونيكر بوظيفة دلتا ديراك.

دعونا نلقي نظرة فاحصة على هذه الأدوات.

يتم استبدال المبالغ بالتكاملات . إذا أردنا حقًا الحفاظ على الدقة ، فسنبدأ باستبدال المحور x بمجموعة منفصلة من النقاط مفصولة بفواصل صغيرة جدًا ε ، ثم ننتقل إلى الحد ε → 0. سيستغرق الأمر عدة صفحات لتبرير كل خطوة. ولكن يمكننا تجنب هذا الإزعاج مع بعض التعريفات البديهية ، مثل استبدال المبالغ بالتكاملات. من الناحية التخطيطية ، يمكن كتابة هذا النهج على النحو التالي:



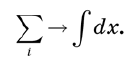
على سبيل المثال ، إذا كنت بحاجة إلى حساب المساحة تحت المنحنى ، فسيتم تقسيم المحور x إلى أجزاء صغيرة ، ثم تتم إضافة مناطق عدد كبير من المستطيلات ، تمامًا كما هو الحال في التحليل الرياضي الأولي. عندما نترك الأجزاء تتقلص إلى الحجم صفر ، يصبح المجموع جزءًا لا يتجزأ.

خذ بعين الاعتبار الدعامة 〈Y | و ket | Y〉 وتحديد منتجها الداخلي. الطريقة الواضحة للقيام بذلك هي استبدال الجمع في المعادلة (1.2) بالتكامل. نحدد المنتج الداخلي على النحو التالي:



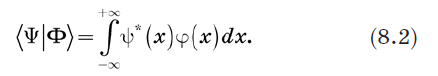يتم استبدال الاحتمالات بكثافات الاحتمال . بعد ذلك ، نحدد P (x) = Y * (x) Y (x) بكثافة الاحتمال للمتغير x. لماذا بكثافة الاحتمال وليس فقط بالاحتمال؟ إذا كان x متغيرًا مستمرًا ، فإن احتمال أن يأخذ أي قيمة محددة تمامًا يكون عادة صفرًا. لذلك ، من الأصح طرح السؤال بهذه الطريقة: ما هو احتمال أن يقع x بين قيمتين x = a و x = b؟ يتم تحديد كثافة الاحتمال بحيث يتم إعطاء هذا الاحتمال من قبل التكامل



نظرًا لأن الاحتمال الإجمالي يجب أن يكون 1 ، يمكننا تحديد تطبيع المتجه كـ



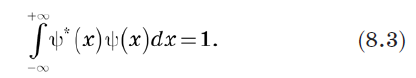يتم استبدال رمز دلتا كرونيكر بوظيفة دلتا ديراك . حتى الآن ، كان كل شيء مألوفًا للغاية. تعد وظيفة Dirac Delta شيئًا جديدًا. دالة دلتا هي تمثيلية لرمز دلتا Kronecker dij ، والتي بحكم التعريف هي 0 إذا i ≠ j ، و 1 إذا i = j. ولكن يمكن تعريفه بطريقة أخرى. ضع في اعتبارك أي ناقل متجه في مساحة محدودة الأبعاد. من السهل رؤية أن رمز دلتا كرونيكر يفي بالشرط



هذا يرجع إلى حقيقة أن المصطلحات مع j = i فقط هي غير صفرية في هذا المبلغ. أثناء الجمع ، يقوم رمز Kronecker بتصفية جميع مكونات F باستثناء Fi. سيكون التعميم الواضح لهذا هو تحديد وظيفة جديدة لها نفس خاصية التصفية عند استخدامها تحت التكامل. وبعبارة أخرى ، نحن بحاجة إلى كيان جديد d (x - x ') ، له خاصية أنه لأي وظيفة F (x)



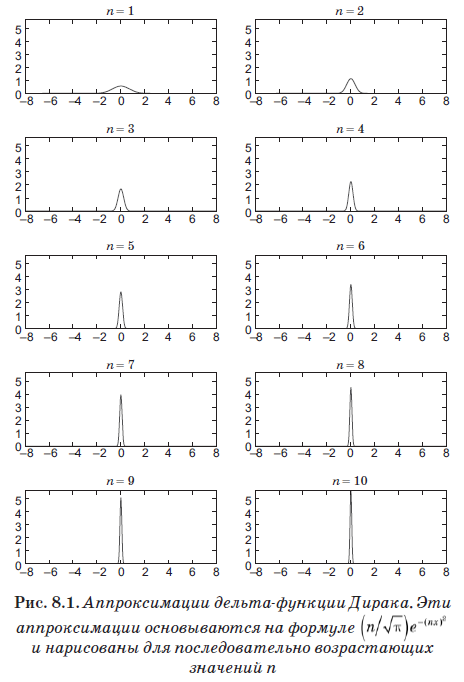
تحدد المعادلة (8.4) كيانًا جديدًا يسمى دالة Dirac delta ، والتي تبين أنها أهم أداة في ميكانيكا الكم. ولكن على الرغم من اسمها ، فهذه ليست وظيفة بالمعنى المعتاد. تساوي صفر حيث x ≠ x '، لكن عندما تكون x = x' تذهب إلى ما لا نهاية. في الواقع ، إنها بلا حدود بما يكفي بحيث تكون المساحة تحت d (x) تساوي 1. تقريبًا ، هذه الوظيفة غير صفرية على الفاصل الصغير اللامتناهي ε ، ولكن في هذا الفاصل لها القيمة 1 / ε. وبالتالي ، فإن المنطقة تحته تساوي 1 ، والأهم من ذلك ، أنها تلبي المعادلة (8.4). الوظيفة



يقترب من دالة دلتا بشكل جيد لقيم كبيرة جدا من n. في الشكل. 8.1 يوضح هذا التحسين مع زيادة قيم n. على الرغم من حقيقة أننا استقرنا على n = 10 ، أي قيمة صغيرة جدًا ، لاحظ أن الرسم البياني قد أصبح بالفعل قمة ضيقة وحادة جدًا.



»يمكن العثور على مزيد من المعلومات حول الكتاب على موقع الناشر على الويب
» المحتويات
» مقتطفات

لقراء هذه المدونة ، خصم 20 ٪ على القسيمة - Sasskind