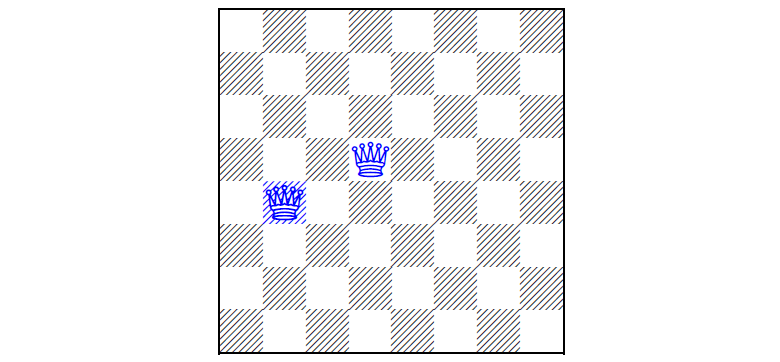
الإصدار الأول من اللغز في عام 1850 ، عندما يتم تثبيت ملكتين مسبقًا على اللوحة ، ويجب على اللاعب ترتيب الملكات المتبقية (للحصول على حلين للمشكلة ، انظر تحت القطع)مشكلة N الملكات هي وضع N الملكات على لوحة N × N بحيث لا توجد ملكة تحت معركة الأخرى ، مع تثبيت العديد من الملكات مسبقًا على اللوحة. أي أنه في النهاية ، لا يجب أن تكون ملكتان على نفس الخط أو قطريًا. تم صياغة المشكلة لأول مرة في عام 1848 ، وفي عام 1850 توصلوا إلى متغير لغز ، عندما تم وضع عدد معين من الملكات على اللوحة مسبقًا ، ويجب على اللاعب ترتيب الباقي ، إن أمكن.
نشر باحثون في جامعة سانت أندروز (اسكتلندا) مقالًا
علميًا يثبت أن مشكلة N-Queens ليست فقط # P-كاملة ، ولكنها أيضًا مكتملة NP. علاوة على ذلك ، فإن معهد كلاي للرياضيات (الولايات المتحدة) مستعد لدفع مليون دولار لأي شخص يمكنه تحسين الحل لهذه المشكلة كمشكلة إثبات P = NP.
كما تعلمون ، في نظرية التعقيد ، #P هي فئة من المشاكل التي يكون حلها هو عدد الحالات الناجحة ، أي إكمال حالات القبول في بعض الحالات الحسابية لآلة تورينج غير القطعية التي تعمل في وقت متعدد الحدود. ترتبط المشاكل الحسابية للفئة #P (مشاكل العد) بمشكلات القرار المقابلة للفئة NP.
يلاحظ العلماء أن هذه المهمة قد تكون الأبسط بين المهام المكتملة NP لشرح جوهر هذه المشاكل لأي شخص يعرف قواعد لعبة الشطرنج. هذه المهمة لها قصة مثيرة جدا للاهتمام. في وقت من الأوقات ، جذبت انتباه غاوس ، التي ارتكبت حتى خطأ صغيرًا في قرارها (على لوحة 8 × 8 ، أبلغ عن 76 قرارًا ، لكنه بعد ذلك اعترف بأربعة منها خاطئة ، بحيث بقي 72 فقط ، وبعد ذلك أنشأ غاوس جميع القرارات الـ 92 لوحة 8 × 8).
جذب تعميم مشكلة لوحة N × N انتباه العديد من علماء الرياضيات. على مدى نصف القرن الماضي ، تم نشر العديد من الأوراق العلمية المخصصة لهذه المشكلة. تم اقتباس ستة منها على الأقل أكثر من 400 مرة على الباحث العلمي من Google: هذا هو Golomb & Baumert ، 1965 ؛ بيتنر ورينجولد ، 1975 ؛ ماكوورث وفرويدر ، 1985 ؛ Minton ، Johnston ، Philips ، & Laird ، 1992 ؛ Selman ، Levesque & Mitchell ، 1992 ؛ كروفورد ، جينسبيرج ، لوكس ، وروي ، 1996.
غالبًا ما يُساء تقدير مدى تعقيد مشكلة N-Queens. حتى في الأعمال التي يتم الاستشهاد بها بكثرة ، غالبًا ما يطلق عليها مشكلة NP-hard (NP-hard) ، ولكنها لن تكون إلا إذا P = NP. في الواقع ، النسخة الحسابية للمشكلة ، أي تحديد عدد الحلول
لملكات N ، هي
تسلسل A000170 من موسوعة Online Integer Sequences. هذا التسلسل معروف الآن كحد أقصى لـ n = 27 ، حيث يتجاوز عدد الحلول 2.34 × 10
17 . لا يوجد حل أكثر فعالية للمشكلة معروف من البحث الشامل البسيط. لذلك ، بالنسبة إلى n = 27 في عام 2016 ، تم استخدام بحث متوازي واسع النطاق على FPGA.
في الوقت نفسه ، إذا بدأ الكمبيوتر في تعداد المواضع المحتملة للملكات على لوحة خلية 1000 × 1000 ، فسيتم تحميل هذه المهمة إلى الأبد. وفقًا للعلماء ، إذا وجد شخص ما طريقة سريعة وفعالة حقًا لحلها ، فسيكون قادرًا على الاستفادة منها أكثر من مليون دولار من معهد كلاي للرياضيات. يقول أستاذ علوم الكمبيوتر ، إيان جنت ، أحد مؤلفي العمل العلمي: "إذا كتبت برنامجًا يمكنه حل المشكلة بسرعة كبيرة ، فيمكنك تعديله لحل العديد من المهام المهمة التي نواجهها كل يوم". "من بينها مشاكل تافهة ، مثل العثور على أكبر مجموعة من أصدقائك على Facebook الذين لا يعرفون بعضهم البعض ، أو مهام مهمة جدًا ، على سبيل المثال ، رموز الاختراق التي تضمن أمان جميع معاملاتنا عبر الإنترنت."
لكن هذه افتراءات نظرية بحتة. من الناحية العملية ، لم يقترب أحد حتى الآن من حل مشكلة الملكات بطريقة سريعة وفعالة. لإثبات أن هناك طريقة أكثر فاعلية لحل المشكلة من التعداد البسيط لجميع الخيارات ، سيقدمون مليون دولار.
تم
نشر مقال علمي في أغسطس 2017 في مجلة
Journal of Artificial Intelligence Research (doi: 10.1613 / jair.5512 ،
pdf ).
PS Two حلول لمشكلة KDPV:
