
"الحد الأدنى النظري" هو كتاب لأولئك الذين فاتهم دروس في الفيزياء في المدرسة والمعهد ، ولكنهم يندمون بالفعل على ذلك. هل تريد فهم أساسيات العلوم الطبيعية وتعلم كيفية التفكير والتفكير كما يفعل الفيزيائيون المعاصرون؟ في شكل أصلي وغير قياسي ، يقدم العلماء الأمريكيون المشهورون ليونارد ساسكيند وجورج جرابوفسكي دورة تمهيدية في الرياضيات والفيزياء للعقول الفضولية.
على عكس الكتب غير الروائية الأخرى التي تحاول شرح قوانين الفيزياء بطريقة يمكن الوصول إليها ، وتجنب المعادلات والصيغ بذكاء ، يعلم المؤلفون القارئ الأسس الكلاسيكية للعلوم الطبيعية. يقدم الكتاب منهجية التدريس الأصلية الخاصة به ، تكملها محاضرات فيديو منشورة على
theoreticalminimum.com .
المحاضرة 9. سائل الطور و نظرية جيبس - نظرية ليوفيل
أحب Lenny النظر إلى النهر ، خاصة لمشاهدة البقع الصغيرة التي تطفو على السطح. حاول أن يتخيل كيف سينتقلون بين الحجارة أو الوقوع في دوامات. لكن مجرى النهر ككل - الحركة المجمعة لكمية كبيرة من الماء ، مع الجداول التي تفصل ، تتلاقى وتتفوق على بعضها البعض - كانت خارجة عن فهمه.
سائل الطوريعد التركيز على ظروف أولية محددة واتباع مسار منفصل في مساحة الطور أمرًا طبيعيًا جدًا للميكانيكا الكلاسيكية. ولكن هناك أيضًا وجهة نظر أوسع تغطي عائلة كاملة من المسارات. بدلاً من وضع طرف القلم الرصاص في نقطة معينة في مساحة الطور وتتبع المسار الوحيد من هناك ، سنحاول القيام بشيء أكثر طموحًا. تخيل أن لدينا عدد لا حصر له من أقلام الرصاص ، ونستخدمها حتى نملأ مساحة الطور بشكل موحد بالنقاط (بالتجانس ، أعني أن كثافة النقاط في الفضاء q ، p هي نفسها في كل مكان). اعتبر هذه النقاط كجسيمات تشكل سائلًا تخيليًا يملأ فراغ المرحلة.
الآن دع كل نقطة تتحرك وفقًا لمعادلات هاميلتون للحركة:
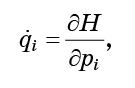
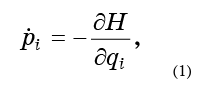
بحيث يتدفق مائعنا إلى ما لا نهاية عبر مساحة الطور.
المذبذب التوافقي هو مثال أولي جيد. رأينا في المحاضرة 8 أن كل نقطة تتحرك في مدار دائري بسرعة زاوية ثابتة. (دعني أذكرك أننا نتحدث عن المرحلة ، وليس عن إحداثيات الفضاء. في التنسيق ، يتحرك المذبذب ذهابًا وإيابًا في بُعد واحد.) يقوم السائل بأكمله ككل بحركة صلبة ، يدور بشكل موحد حول أصل مساحة المرحلة.
نعود الآن إلى الحالة العامة. إذا كان عدد الإحداثيات هو N ، فإن مساحة الطور والسائل فيه تكون ثنائية الأبعاد. يتدفق السائل ، ولكن بطريقة محددة للغاية. تدفقه له خصائص خاصة. أحدها هو أنه إذا بدأت نقطة ما بطاقة معينة - أي بقيمة معينة من H (q ، p) - فإنها تخزن قيمة الطاقة هذه. يتم تحديد أسطح الطاقة الثابتة (على سبيل المثال ، مع طاقة تساوي E) بواسطة المعادلة H (q ، p) = E. (2)
لكل قيمة E ، لدينا معادلة واحدة مع متغيرات مساحة الطور 2N التي تحدد سطح البعد 2N - 1. وبعبارة أخرى ، كل قيمة E لها سطحها الخاص ؛ عند تجاوز جميع قيم E ، تملأ هذه الأسطح مساحة الطور بالكامل. يمكننا أن ننظر في مساحة الطور مع الأسطح المعطاة بواسطة المعادلة (2) كخريطة للخطوط (الشكل 1) ، حيث لا تمثل الأفقية الارتفاع ، ولكن قيم الطاقة. إذا كانت نقطة السائل على سطح معين ، فستبقى عليه إلى الأبد. هذا هو قانون الحفاظ على الطاقة.
مساحة طور المذبذب التوافقي ثنائي الأبعاد ، والأسطح الطاقية على شكل دوائر:
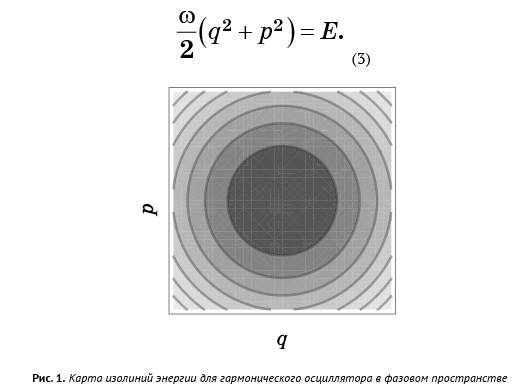
في الحالة العامة ، تكون أسطح الطاقة في النظام الميكانيكي معقدة للغاية بحيث لا يمكن تصورها ، لكن المبدأ يظل كما هو:
تملأ أسطح الطاقة مساحة الطور كطبقات ، ويتحرك التدفق بحيث تبقى النقاط على السطح الذي كانت عليه في الأصل .
تذكير قصيرأود أن أتوقف هنا وأتذكر ما قيل في المحاضرة الأولى ، حيث نوقشت العملات والنرد وأبسط الأفكار حول قوانين الحركة. وصفنا هذه القوانين بمجموعة من الأسهم التي تربط النقاط التي تمثل حالات النظام. كما أوضحنا أن القوانين مقبولة وغير مقبولة ، بينما يمكن عكسها. خلاصة القول هي أنه يجب أن يكون لكل نقطة سهم وارد واحد وسهم صادر واحد بالضبط. إذا تجاوز عدد الأسهم الواردة ، على الأقل ، عدد الأسهم الصادرة (وهذا ما يسمى التقارب) ، فإن هذا القانون لا رجعة فيه. وينطبق الشيء نفسه على الحالة عندما يكون هناك المزيد من الأسهم الصادرة من تلك الواردة (يسمى هذا الاختلاف). إن اختلاف وتقارب الأسهم ينتهكان قابلية الانعكاس وممنوعين. حتى الآن ، لم نعد إلى خط التفكير هذا. الآن حان الوقت.
التدفق والاختلاففكر في بعض الأمثلة البسيطة لتدفق السوائل في الفضاء العادي. للحظة ، ننسى مساحة الطور وننظر فقط في مائع عادي يتحرك في الفضاء ثلاثي الأبعاد المعتاد مع محاور تشير إلى x ، y ، z. يمكن وصف التدفق من خلال
مجال السرعة . مجال السرعة
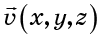
يتحدد بضبط متجه السرعة عند كل نقطة في الفضاء (الشكل 2).
يمكنك أيضًا وصف حقل السرعة بمكونات السرعة:
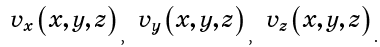
أيضًا ، قد تعتمد السرعة عند نقطة معينة على الوقت ، ولكن لنفترض أنه لا يوجد مثل هذا الاعتماد. في هذه الحالة ، يسمى التدفق
ثابتًا .
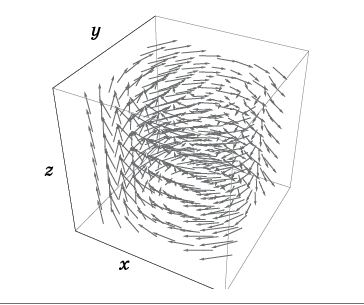
التين. 2. مجال السرعة
يأخذ نفس المبلغ. وهذا يعني أيضًا أن كثافة السائل - عدد الجزيئات لكل وحدة حجم - هي نفسها في كل مكان وثابتة بمرور الوقت. بالمناسبة ، مصطلح "عدم الانضغاطية" يعني أيضًا عدم القابلية للاستبدال. وبعبارة أخرى ، لا يمكن زيادة حجم السائل. خذ بعين الاعتبار الخلية المكعبة الصغيرة التي تحددها الشروط:
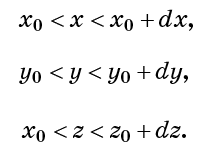
يشير عدم التوافق إلى أن عدد نقاط السوائل في كل خلية من هذه الخلايا ثابت. هذا يعني أيضًا أن إجمالي تدفق السوائل الذي يدخل الخلية (لكل وحدة زمنية) يجب أن يكون صفرًا. (عدد نقاط التدفق الذي يدخل إليه نفس العدد.) ضع في اعتبارك عدد الجزيئات التي تمر لكل وحدة زمنية عبر سطح الخلية x = x0. سيكون متناسبًا مع سرعة التدفق على هذا السطح vx (x0).
إذا كانت السرعة vx هي نفسها عند x0 وعند x0 + dx ، فإن التدفق إلى الخلية من خلال x = x0 سيكون هو نفسه التدفق من خلال x = x0 + dx. ولكن إذا تغير vx في جميع أنحاء الخلية ، فسيكون هذان التدفقان غير متوازنين. سيكون التدفق الكلي الذي يدخل الخلية من خلال هذين الوجهين متناسبًا
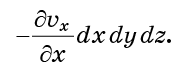
تنطبق نفس الاعتبارات بالضبط على الوجوه y0 و y0 + dy ، وكذلك z0 و z0 + dz. إذا تمت إضافتها جميعًا ، فعندئذ يكون التدفق الكلي للجزيئات في الخلية (التدفق ناقص التدفق الخارج)
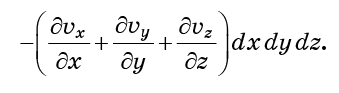
يسمى الجمع بين المشتقات بين قوسين اختلاف مجال المتجه
ويتم تعيينه
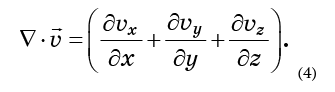
يعكس الاختلاف درجة تشتت الجزيئات ، أو الزيادة في الحجم الذي تشغله. إذا كان السائل غير قابل للانضغاط ، فيجب ألا يتغير هذا الحجم ، مما يعني أن الاختلاف يجب أن يكون صفرًا.
إحدى طرق فهم عدم الانضغاطية هي تخيل كل جزيء أو نقطة على أنها تحتل حجمًا لا يمكن تغييره. لا يمكن ضغطها في حجم أصغر ، فهي لا تختفي ولا تظهر من العدم. بقليل من التفكير ، يمكنك أن ترى مدى تشابه عدم الانضغاط والعكس. في الأمثلة التي قمنا بتحليلها في المحاضرة 1 ، حددت الأسهم أيضًا نوعًا من التدفق. وبشكل أساسي ، كان هذا الدفق غير قابل للضغط ، على الأقل إذا كان قابلاً للعكس. السؤال الطبيعي الذي ينبع من هذا هو: هل التدفق في طور الفضاء قابل للعكس؟ الجواب نعم ، إذا كان النظام يلبي معادلات هاميلتون. والنظرية التي تعبر عن عدم التوافق هذه تسمى نظرية ليوفيل.
نظرية ليوفيلدعونا نعود إلى تدفق السوائل في مساحة الطور ونأخذ في الاعتبار مكونات سرعة المائع عند كل نقطة في مساحة الطور. ليست هناك حاجة للقول أن مائع الطور ليس ثلاثي الأبعاد في الإحداثيات س ، ص ، ض. وهو سائل ثنائي الأبعاد في الإحداثيات pi ، qi.
وبالتالي ، هناك 2N مكونات مجال السرعة - واحد لكل إحداثي q وكل إحداثي p. دعهم

يمكن تعميم مفهوم الاختلاف المعبر عنه بالمعادلة (4) بسهولة على أي عدد من الأبعاد. في ثلاثة أبعاد ، هذا هو مجموع مشتقات مكونات السرعة في الاتجاهات المقابلة. بنفس الطريقة ، يتم تحديده لأي عدد من الأبعاد. في حالة مساحة الطور ، يكون اختلاف التدفق هو مجموع أعضاء 2N:
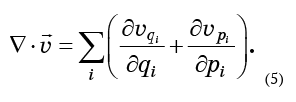
إذا كان السائل غير قابل للضغط ، فيجب أن يكون هذا التعبير صفرًا. لحساب ذلك ، تحتاج إلى معرفة مكونات مجال السرعة - بالطبع ، ليست سوى سرعات جزيئات مائع الطور.
يتم تحديد متجه التدفق عند نقطة معينة بسرعة جسيم وهمي عند تلك النقطة. بعبارة أخرى
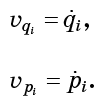
علاوة على ذلك
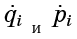
- هذه فقط الكميات التي تدخل معادلات هاميلتون (1):
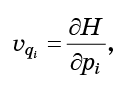
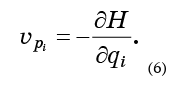
كل ما يجب فعله هو استبدال المعادلات (6) في الصيغة (5) والحصول على
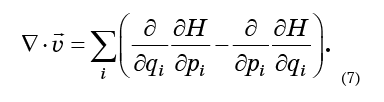
مذكرا بأن المشتق الثاني للشكل
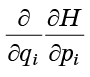
لا يعتمد على ترتيب التمايز ، سوف نفهم أن شروط المعادلة (7) تدمر بعضها البعض بالضبط في أزواج:
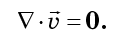
لذا ، فإن سائل الطور غير قابل للضغط. في الميكانيكا الكلاسيكية ، يسمى عدم انضغاط مائع الطور نظرية ليوفيل ، على الرغم من أنه لا علاقة له تقريبًا بعالم الرياضيات الفرنسي جوزيف ليوفيل. تم نشره لأول مرة في عام 1903 من قبل الفيزيائي الأمريكي العظيم يوشيا ويلارد جيبس ، وهو معروف أيضًا باسم نظرية جيبس - ليوفيل.
حددنا عدم انضغاط السائل من خلال اشتراط أن تكون الكمية الإجمالية للسائل الذي يدخل أي خلية صغيرة صفرًا. هناك تعريف آخر مكافئ تمامًا. تخيل كمية سائلة في وقت ما. يمكن أن يكون لهذا الحجم أي شكل: كروي ، مكعب ، يشبه القطرة - أيا كان. الآن سنتابع حركة جميع نقاط هذا المجلد. بعد مرور بعض الوقت ، ستكون قطرة من السائل في مكان مختلف ويكون لها شكل مختلف. ولكن إذا كان السائل غير قابل للانضغاط ، فسيظل حجم القطرة كما كان في الأصل. حتى نتمكن من إعادة صياغة نظرية Liouville:
يتم الحفاظ على
الحجم الذي تشغله قطرة من سائل الطور في الوقت المناسب .
ضع في اعتبارك مثالًا على مذبذب متناسق حيث يدور مائع حول نقطة مرجعية. من الواضح أن الهبوط يحتفظ بالحجم ، حيث يتم تقليل كل حركته إلى دوران الحالة الصلبة. يبقى شكل الهبوط دون تغيير ، ولكن هذا هو الحال بالنسبة لمذبذب التوافقي. تأمل في مثال آخر. لنفترض أن هاميلتون لديه الشكل H = pq.
ربما يبدو لك هذا على عكس هاملتون ، على الرغم من أنه صحيح تمامًا. نستمد معادلات الحركة:
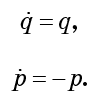
وفقًا لهذه المعادلات ، تزداد q بشكل أسي بمرور الوقت ، وتنخفض p بشكل أسي بنفس السرعة. وبعبارة أخرى ، يضغط التدفق السائل على المحور ص ، بينما يوسعه في نفس الوقت على طول المحور q إلى نفس المدى. أي انخفاض يمتد على طول q والعقود على طول ص. من الواضح أن الهبوط يواجه تشوهات هائلة ، لكن حجم طوره لا يتغير.
نظرية ليوفيل هي أقرب نظير يمكن تخيله لنوع اللارجعة الذي ناقشناه في المحاضرة 1. في ميكانيكا الكم ، يتم استبدال نظرية ليوفيل بنسخة كمية تسمى الوحدة. الوحدة هي أكثر تشابهًا مع ما ناقشناه في المحاضرة 1 ، ولكن هذا هو موضوع العدد التالي من الحد الأدنى النظري.
»يمكن العثور على مزيد من المعلومات حول الكتاب على
موقع الناشر على الويب»
تعجب»
مقتطفاتلقراء هذه المدونة ، خصم 20 ٪ على القسيمة -
الحد الأدنى النظري