بعد صب الرمل على صفيحة مرنة متأرجحة ، يمكن للمرء أن يرى تشكيل أشكال Hladni . غالبًا ما تكون بمثابة مثال على "الجمال الطبيعي" للظواهر الفيزيائية ، على الرغم من أن وراءها فيزياء بسيطة إلى حد ما للإثارة الرنانة للموجات الواقفة. وقليل من الناس يهتمون بالميزة الغريبة لهذه الأرقام: الخطوط التي عليها تتجنب التقاطعات ، كما لو أن بعض القوة تصدهم. دعونا نحاول أن نفهم أي نوع من الفيزياء مخفي وراء هذا التنافر وكيف يرتبط بنظرية الكم من الفوضى.

موجات واقفة

كما نعلم ، يمكن للأجسام المرنة أن تحدث اهتزازات معقدة نوعًا ما ، تتقلص خلالها ، وتمتد ، تنحني وتلتف. ومع ذلك ، يمكن تمثيل اهتزازات أي جسم مرن كمزيج من اهتزازات عادية أبسط متراكبة على بعضها البعض. هذه هي الطريقة التي تبدو بها العديد من الاهتزازات العادية لجسم مرن بسيط - سلسلة ممتدة أحادية البعد.

يتم تمثيل كل تذبذب طبيعي بموجة واقفة ، والتي ، على عكس الموجة المتنقلة ، تقف ثابتة ولها نمطها الخاص لتوزيع اتساع التذبذبات في الفضاء. في هذا الشكل ، يمكن تمييز antinodes - النقاط التي يصل فيها اتساع التذبذبات إلى أقصى حد ، والعقد - نقاط ثابتة يكون فيها اتساع التذبذب صفرًا. بالإضافة إلى ذلك ، تتأرجح كل موجة كهذه بترددها الخاص . في حالة وجود سلسلة ، كما ترون ، يزداد تواتر تذبذبات الموجة الدائمة مع زيادة عدد العقد والضد.


دعونا الآن نلقي نظرة على نظام ثنائي الأبعاد ، ومثال على ذلك غشاء رقيق مرن ممتد فوق إطار صلب. تبدو الاهتزازات العادية للغشاء المستدير أكثر تعقيدًا مما كانت عليه في حالة الخيط ، وبدلاً من العقد النقطية الفردية ، توجد خطوط عقدية يكون الغشاء على طولها ثابتًا.


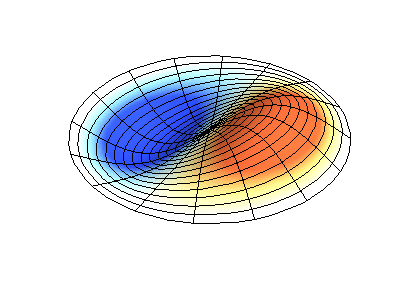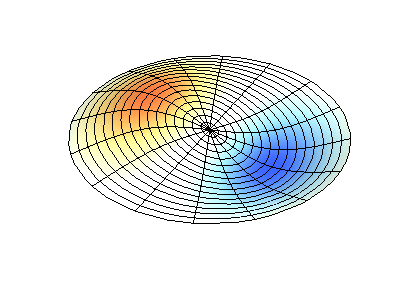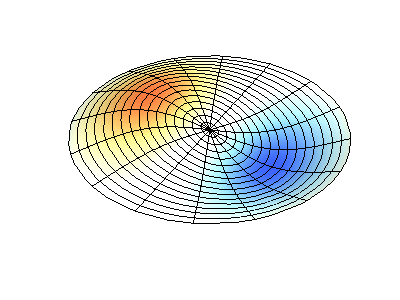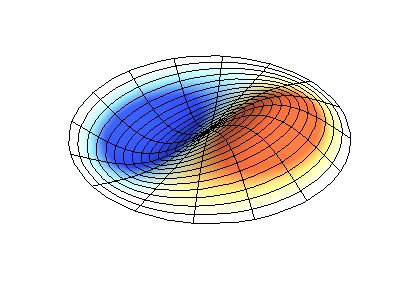
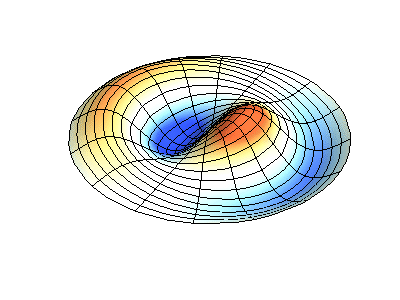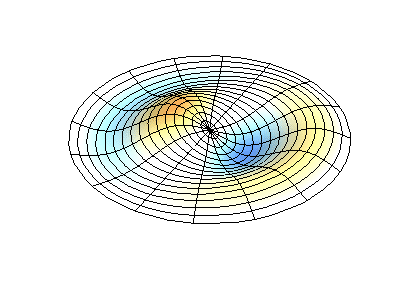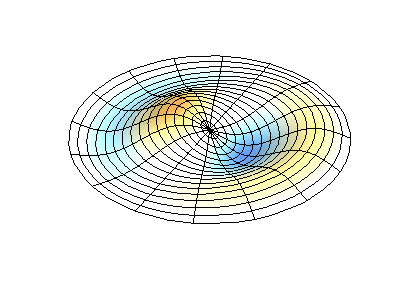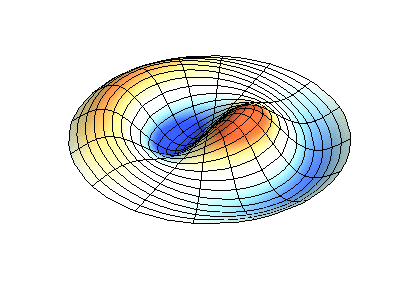
اهتزازات عادية للغشاء الدائري بحواف ثابتة. المصدر


يظهر اللون الأخضر خطوط العقدة.

في الغشاء المستدير ، يمكن أن تتقاطع الخطوط العقدية ، وهي دوائر وأجزاء على طول نصف القطر ، بزاوية قائمة. إذا كانت حواف الغشاء لها شكل تعسفي ، فإن العثور على ترددات الاهتزازات العادية وأنماط العقد والضد تتحول إلى مشكلة لا يمكن حلها إلا باستخدام الكمبيوتر.

لمحة عن اتساع تذبذبات الموجات الواقفة على الأغشية على شكل مربع به ثقب ورقاقات ثلجية كوتش وسطح هريرة .

المعادلات التي تصف تذبذبات لوحة مرنة رقيقة تختلف عن معادلات تذبذب الغشاء ، حيث أن الصفيحة لها صلابة خاصة بها ، في حين أن الغشاء ناعم وربيعي فقط بسبب التوتر من القوى الخارجية. ومع ذلك ، هناك أيضًا مجموعات من الاهتزازات العادية ، والتي تعتمد رسوماتها بشكل كبير على شكل الحدود.

شخصيات هالدني

كما هو مذكور أعلاه ، في الحالة العامة ، تكون اهتزازات الجسم عبارة عن مجموعة من مجموعة كاملة من الاهتزازات العادية متحمسة فيها. تسمح لك ظاهرة الرنين بإثارة واحدة من الاهتزازات العادية التي نحتاجها بشكل انتقائي - لهذا نحتاج إلى تأرجح الجسم باستخدام قوة خارجية بتردد يساوي التردد الطبيعي للتذبذب الطبيعي.

يظهر الفيديوان أدناه مخططًا نموذجيًا للحصول على أشكال Hladni: يتم إرفاق لوحة مرنة في المركز بمولد من الاهتزازات الميكانيكية ، والتي يزداد ترددها تدريجيًا. تكون اهتزازات اللوحة العادية مع أنماط العقد والعقد المضطربة متحمسة عندما يطابق تردد المذبذب صدى الترددات الطبيعية لهذه الاهتزازات (تظهر الترددات الطبيعية في الفيديو في الزاوية اليسرى السفلى).

فيما يلي نسخة من نفس الفيديو حيث يمكن تقدير ترددات الاهتزازات العادية عن طريق الأذن.

وهنا أجمل قليلاً.

نرى أنماطًا للعقدة والأضداد بسبب حقيقة أن تيارات الهواء بالقرب من صفيحة متأرجحة تضرب حبيبات الرمل إلى الخطوط العقدية لموجة واقفة ^(*) . وهكذا ، فإن أرقام Hladni تُظهر لنا أنماطًا من الخطوط العقديّة للاهتزازات العادية للوحة مرنة.

العديد من الشخصيات هالدني على السطح العلوي من الغيتار. المصدر

مثال آخر على الموجات الطبيعية هو الموجات الواقفة على سطح الماء. يتم وصفها بواسطة معادلة تختلف عن معادلات اهتزاز الألواح والأغشية ، ولكنها تتبع نفس القوانين النوعية ، وبمساعدتها من الممكن الحصول على نظائر شخصيات Hladni.

جزيئات دقيقة على سطح الماء في أوعية بمختلف الأشكال. يظهر الخط الأسود مقياسًا يبلغ 2 ملم. المصدر

الفوضى الكلاسيكية

لذا ، رأينا أنه في حالة الغشاء المستدير ، تكون الخطوط العقدية نظريًا! - تتقاطع الخطوط العقدية بشكل ملحوظ ، في نفس الوقت ، على أشكال Hladni على لوحات مربعة أو أكثر تعقيدًا ، وتتجنب التقاطعات. لفهم سبب هذه الأنماط ، سيتعين علينا القيام برحلة قصيرة في نظرية الفوضى.

الفوضى الكلاسيكية هي خاصية للأنظمة الميكانيكية ، تتكون في اعتماد قوي للغاية على مسار حركتها على التغيرات في الظروف الأولية. تُعرف هذه العلاقة أيضًا باسم " تأثير الفراشة ". يمكن العثور على مثال حي على السلوك الفوضوي في محاولات التنبؤ بالطقس: لا يسمح نظام المعادلات الذي يصف حركة الغلاف الجوي والمحيطات بتنبؤات دقيقة بما فيه الكفاية في أوقات طويلة بسبب الأخطاء المتزايدة بشكل كبير بسبب عدم الدقة الصغيرة في البيانات الأولية ^(**) .

تم نشر ظاهرة الفوضى بشكل علني وشائع من قبل عالم الأرصاد وعالم الرياضيات إدوارد لورينز ، الذي اكتشف أن حسابين لتنبؤات الطقس بدءًا من ظروف أولية قريبة جدًا لا يمكن تمييزهما تقريبًا في البداية ، ولكن في مرحلة ما بدأوا في الاختلاف جذريًا.

حسابان من قبل إدوارد لورينز ، بدءًا من القيم الأولية القريبة 0.506 و 0.506127. المصدر

إن أبسط الأنظمة ، التي يمكن من خلالها دراسة الفوضى ، على سبيل المثال ، هي البلياردو - وهي أجزاء من سطح مستو يمكن أن تتدحرج على طولها الكرة دون احتكاك ، ترتد بشكل مرن تمامًا عن الجدران الصلبة. في البلياردو الفوضوية ، تتباعد مسارات الكرة ، التي لها اختلافات طفيفة في البداية ، بشكل كبير في وقت لاحق. مثال على البلياردو الفوضوية هو بلياردو سيناء الموضح أدناه ، وهو عبارة عن تجمع مستطيل مع عقبة دائرية في المركز. كما سنرى ، وبسبب هذه العقبة بالتحديد يصبح البلياردو فوضويًا.

مسارين مختلفين بشكل كبير في الكرة الأرضية في بلياردو سيناء. المصدر

أنظمة متكاملة وفوضوية

تسمى الأنظمة الميكانيكية غير الفوضوية بالتكامل ، ومع مثال البلياردو ، يمكنك أن ترى بوضوح الفرق بين الأنظمة القابلة للتكامل والفوضى.

البلياردو المستطيل والمستدير قابل للتكامل بسبب شكله المتناظر ^(***) . حركة الكرة في هذه البلياردو هي ببساطة مزيج من حركتين دوريتين مستقلتين. في البلياردو المستطيلة ، هذه حركات ترتد من الجدران أفقياً ورأسياً ، وهي حركة على طول نصف القطر وحركة زاوية في دائرة حول المركز. يتم حساب هذه الحركة بسهولة ولا تظهر سلوكًا فوضويًا.

مسارات الكرة في البلياردو القابلة للتكامل.

البلياردو ذات الشكل الأكثر تعقيدًا ، والتي لا تمتلك تناظرًا عاليًا مثل دائرة أو مستطيل ، فوضوي ^(****) . واحد منهم رأيناه أعلاه هو بلياردو سيناء ، حيث يتم تدمير تناظر المستطيل من خلال تضمين دائري في المركز. وكثيرا ما تعتبر البلياردو "ملعب" والبلياردو على شكل القواقع باسكال. تتحرك الكرة في البلياردو الفوضوي على طول مسارات معقدة للغاية ولا تتحلل إلى حركات دورية أبسط.

مسار الكرة في الفوضى البلياردو "استاد" و "حلزون باسكال".

هنا يمكنك بالفعل تخمين أن وجود تقاطعات بين الخطوط في أشكال Hladni يتم تحديده من خلال ما إذا كانت اللوحة لها شكل بلياردو قابل للتكامل أو فوضوي. هذا واضح في الصور أدناه.

صفائح مستديرة Hladni ، توضح خصائص البلياردو المتكاملة. المصدر

شرح خصائص البلياردو الفوضوي في صفيحة الحلادني على شكل "ملعب" بلياردو ، حالة الكمان والساحة ، التي تم كسر تماثلها بتثبيت دائري في المركز (تناظرية بلياردو سيناء). المصدر

الفوضى الكمومية

كيف نفهم سبب تقاطعات الخطوط العقدية بسبب قابلية البلياردو للتكامل؟ للقيام بذلك ، نحتاج إلى التحول إلى نظرية الكم من الفوضى ، والجمع بين نظرية الفوضى مع ميكانيكا التذبذبات والأمواج. إذا تم وصف الكرة في البلياردو في الميكانيكا الكلاسيكية كنقطة مادية تتحرك على طول مسار معين ، فإن الحركة في الميكانيكا الكمومية توصف بأنها انتشار لموجة تخضع لمعادلة شرودنغر وتنعكس من جدران البلياردو.

مراحل انتشار الموجات في البلياردو الكمومي. في البداية ، تتركز الموجة في نبضة مستديرة وتتحرك من اليسار إلى اليمين ، ثم تنتشر وتنعكس بشكل متكرر من الجدران. المصدر

نفس الشيء في شكل رسوم متحركة ، ولكن بظروف أولية مختلفة قليلاً.

كما هو الحال في اهتزازات الأغشية والألواح ، فإن معادلة شرودنغر التي تصف البلياردو الكمومي تسمح للمرء أن يجد اهتزازات طبيعية في شكل موجات واقفة ، والتي لها نمط مميز من الخطوط العقدية و antinodes ، فرد لكل تذبذب ويعتمد على شكل الحدود.

أمثلة على ملامح اتساع التذبذبات في الأمواج الواقفة في البلياردو الكمومي الفوضوي " حلزون باسكال " و " الاستاد ".

تختلف أنماط الموجات الدائمة في البلياردو الكمومي الفوضوي والمتكامل نوعيًا: تظهر البلياردو القابلة للتكامل أنماطًا متناظرة ومرتبة من الموجات الدائمة ، بينما في البلياردو الفوضوي ، تكون أنماط الموجات الدائمة مربكة للغاية ولا تظهر أي أنماط مرئية (في نهاية المقالة ، سيظهر أن بعض المثير للاهتمام الأنماط لا تزال موجودة).

اتساع التذبذب في الموجات الدائمة للبلياردو المستدير القابل للتكامل (الصف العلوي) والبلياردو الفوضوي على شكل حلزون باسكال (الصف السفلي). المصدر

تعمل الصور الغريبة للاهتزازات الطبيعية في البلياردو الفوضوية أحيانًا كموضوع لدراسة منفصلة. المصدر

يُلاحظ أيضًا اختلاف نوعي في أنماط الخطوط العقدية: في حالة البلياردو الكمّي القابل للتكامل ، نرى عائلات مرتبة من الخطوط المتداخلة ، وفي البلياردو الفوضوية لا تتقاطع هذه الخطوط ، كقاعدة عامة.

أعلاه: خطوط العقدة (خطوط سوداء بين المناطق الزرقاء والحمراء) من موجات دائمة من البلياردو - مستديرة ومستطيلة - بلياردو. في الأسفل: الخطوط العُقدي لإحدى الأمواج الدائمة في البلياردو الفوضوي - ربع بلياردو الاستاد .

تتقاطع أم لا تتقاطع؟

لماذا لا تتقاطع الخطوط العقدية في البلياردو الفوضوي؟ في عام 1976 ، أثبتت عالم الرياضيات كارين Uhlenbeck نظرية أنه بموجبها لا يجب أن تتقاطع الخطوط العقدية للموجات الدائمة للبلياردو الكمومي ، بشكل عام.

في شكل مبسط ، يمكن إظهار ذلك على النحو التالي: افترض أن خطين عقديين يتقاطعان عند نقطة ( x ₀ ، y ₀ ). ولكي يحدث ذلك ، يجب أن تستوفي الوظيفة f ( x، y ) ، التي تحدد اعتماد اتساع الموجة الدائمة على الإحداثيات ، ثلاثة شروط في وقت واحد:

1) يجب أن تكون مساوية للصفر عند النقطة ( x ₀ ، y ₀ ) ، لأن هذه النقطة عقدي.
2) إذا انتقلت من النقطة ( x ₀ ، y ₀ ) في اتجاه الخط العقدي الأول ، فيجب أن تظل f ( x، y ) مساوية للصفر.
3) إذا انتقلت من النقطة ( x ₀ ، y ₀ ) في اتجاه الخط العقدي الثاني ، فيجب أن تظل f ( x، y ) مساوية للصفر.


في المجموع ، لدينا ثلاثة شروط (أو ثلاث معادلات) مفروضة على دالة متغيرين f ( x، y ). كما نعلم ، فإن معادلة واحدة لا تكفي لإيجاد المجهولين x و y المجهولين تمامًا ، معادلتان كافيتان بالفعل لهذا ، وثلاث معادلات أكثر من اللازم. إن نظام المعادلات الثلاث لمجهولين ، بشكل عام ، لن يكون له حلول ، إلا إذا كنا محظوظين بما فيه الكفاية. لذلك ، يمكن أن تتواجد نقاط تقاطع الخطوط العقدية كاستثناء فقط .

في البلياردو القابلة للتكامل ، تنشأ مثل هذه الاستثناءات. كما رأينا أعلاه ، فإن خصائصها الخاصة - إمكانية التنبؤ بالحركة ، وغياب الفوضى ، والأنماط المنتظمة للموجات الدائمة - هي نتيجة لتماثلها العالي. يضمن نفس التناظر تحقيق ثلاثة شروط ضرورية في الوقت نفسه لتقاطعات خطوط العقدة.

دعونا الآن نلقي نظرة فاحصة على أمثلة شخصيات Hladni النموذجية للبيلياردو القابلة للفوضى والتكامل. يوضح الشكل أدناه ثلاث حالات مميزة . على اليسار ، يكون للوحة شكل دائرة ، لذا فإن البلياردو الكمي المقابل قابل للتكامل ، وتتقاطع الخطوط العقدية مع بعضها البعض. في الوسط ، تكون اللوحة مستطيلة ، والتي تتوافق أيضًا مع نظام قابل للتكامل ، ومع ذلك ، فإن التركيب المستدير في المركز ينتهك قليلاً تماثل المستطيل ، لذلك لا تتقاطع الخطوط العقدية في كل مكان. يظهر مثال على نظام فوضوي بحت على اليمين: لوحة على شكل ربع بلياردو سيناء (في الزاوية اليمنى العليا يوجد قطع دائري) ، الخطوط العقدية التي لم تعد تتقاطع.



وبالتالي ، كلما كان شكل اللوحة أقوى - مع مراعاة ربطها - يختلف عن شكل البلياردو المدمج (مثل دائرة أو مستطيل) ، كلما قل تقاطع الخطوط العقدية عليه .

ليس من السهل الحصول على صور هالدنية جميلة بخطوط متقاطعة على لوحة مستديرة. عند الاهتزازات المثيرة مع الحامل المركزي ، يحظر التماثل الدائري للنظام بأكمله تكوين خطوط العقدة الشعاعية ، لذلك سنرى فقط مجموعة مملة من الدوائر (يمكن التغلب على هذه الصعوبة من خلال الاهتزازات المثيرة ليس من المركز ، ولكن من حافة اللوحة باستخدام القوس من الكمان). إذا تم إصلاح اللوحة خارج المركز ، فستصبح أرقام Hladni أكثر إثارة للاهتمام ، ولكن نظرًا لانتهاك التناظر الدائري ، سيتوقف النظام عن التكامل.

لوحة مستديرة ، جبل المركز.

لوحة مستديرة ، تحولت جبل من المركز.

وهنا خيارات مختلفة مع لوحات مستديرة وغير دائرية.

أخيرًا ، قد يلاحظ القارئ اليقظ: لكني أرى أنه في بعض الأحيان تتقاطع الخطوط العقدية حتى على لوحات "فوضوية". كيف يتم ذلك إذا كان تقاطعهم ممنوعًا بواسطة نظرية Uhlenbeck؟

أولاً ، يمكن أن تتجنب الخطوط العقدية التقاطع ، ولكن قبل أن تقترب كثيرًا لدرجة أنه بسبب العرض المحدود لمسار الرمال ، يبدو لنا أن هناك تقاطعًا. ثانيًا ، في الواقع ، لا يوجد حد حاد بين الأنظمة القابلة للتكامل والفوضى.

الخطوط العقدية - تفصل بين المناطق البيضاء والسوداء - في البلياردو الكمومي الفوضوي (اليسار واليمين) ، وفي الحالة الوسطية شبه القابلة للتكامل (في الوسط). في الحالة المتوسطة ، هناك عدة تقاطعات للخطوط العقدية ، بينما في الحالة الفوضوية لا يوجد أي منها على الإطلاق. المصدر

في النظرية الكلاسيكية للفوضى ، تم تكريس نظرية كولموغوروف أرنولد موسر الشهيرة لهذه القضية. وتقول إنه إذا تم انتهاك تناظر النظام الصحيح بشكل طفيف ، فلن يظهر سلوك فوضوي على الفور ، ولكن ، في الغالب ، سيحتفظ بإمكانية التنبؤ بالحركة. على مستوى النظرية الكمومية للفوضى وأرقام هالدني ، يتجلى ذلك في حقيقة أنه في بعض الأماكن يتم الحفاظ على تقاطعات الخطوط العقدية. يحدث هذا إما في نقاط متماثلة بشكل خاص من البلياردو ، أو بعيدًا عن مصدر الاضطراب ، الذي ينتهك تناظر النظام المندمج.

ماذا ايضا؟

ما هو الشيء الآخر المثير للاهتمام في نظرية الكم من الفوضى؟ بالنسبة للقارئ المهتم ، سأذكر ثلاثة أسئلة إضافية لم تعد مرتبطة مباشرة بأرقام هالدني.

1) ظاهرة عالمية تدرسها هذه النظرية هي عالمية الأنظمة الفوضوية. الغالبية العظمى من الأنظمة التي يمكن أن تحدث فيها الاهتزازات العادية هي فوضوية ، وجميعها - بغض النظر عن طبيعتها الجسدية! - الالتزام بالقوانين نفسها. إن ظاهرة العالمية ، التي توصف فيها أنظمة مختلفة تمامًا بنفس الصيغ ، هي نفسها جميلة جدًا وتعمل بمثابة تذكير للوحدة الرياضية للعالم المادي.

إحصائيات المسافات بين الترددات المتجاورة للاهتزازات العادية في الأنظمة الفوضوية ذات الطبيعة الفيزيائية المختلفة ، والتي يتم وصفها في كل مكان بنفس صيغة Wigner-Dyson العالمية. المصدر

2) تتميز أنماط الاهتزازات العادية للبلياردو الفوضوي بميزة مثيرة للاهتمام تسمى "ندوب الكم" . لقد رأينا أن مسارات الكرة في البلياردو الفوضوي عادة ما تكون مربكة للغاية. ولكن هناك استثناءات - هذه مدارات دورية ومسارات مغلقة بسيطة وقصيرة إلى حد ما تقوم الكرة من خلالها بحركة دورية. تسمى الندبات الكمومية بسمك حاد للموجات الدائمة على طول المدارات الدورية.

ندوب الكم في "ملعب" البلياردو ، تسير على طول المدارات الدورية الموضحة بخطوط حمراء وخضراء. المصدر

3) لقد تحدثنا حتى الآن عن أنظمة ثنائية الأبعاد. إذا أخذنا بعين الاعتبار انتشار الموجات في الفضاء ثلاثي الأبعاد ، فيمكن أيضًا أن تنشأ خطوط عقدة هنا يكون فيها طول التذبذب صفرًا. هذا مهم بشكل خاص عند دراسة تكاثف بوز والسيولة الزائدة ، حيث تتحرك الآلاف من الذرات على شكل " موجات من المادة ". من الضروري ، على سبيل المثال ، تحليل بنية خطوط العقدة لموجات المادة في الفضاء ثلاثي الأبعاد ، لفهم كيف ينشأ الاضطراب الكمي ويتطور في أنظمة الموائع الفائقة.

تراكيب متشابكة ثلاثية الأبعاد للخطوط العقدية "لموجات المادة" الدائمة في مكثفات بوز. مصدر .

^(*) إذا كان حجم الجسيمات التي تم سكبها على اللوحة صغيرًا بما فيه الكفاية ، فسيتم إزاحتها ليس إلى العقد ، ولكن إلى antinodes من الموجة الدائمة ، كما هو موضح في هذا العمل التجريبي .

^(**) «» «» , : – , , . .

^(***) – . , , , .

^(****) لكي نكون أكثر دقة ، فإن انتماء البلياردو إلى عدد صحيح أو فوضوي يعتمد على عدد تكاملات الحركة المستقلة- الكميات التي تستمر مع مرور الوقت. تحتوي البلياردو المتكاملة على عنصرين متكاملين للحركة ، في نظام ثنائي الأبعاد هذا يكفي للحل التحليلي الدقيق لمعادلات الحركة. للبلياردو الفوضوي جزء لا يتجزأ من الحركة - الطاقة الحركية للكرة.