عندما أتحدث مع شخص بعيد عن الفيزياء عن الأبعاد الإضافية المحتملة للمساحة غير المعروفة لنا ، فإن أحد الأسئلة الأكثر شيوعًا هو: "كيف تتخيل أبعادًا إضافية؟ يمكنني تخيل ثلاثة فقط ، ولا أفهم كيف أذهب أبعد من ذلك ؛ لا معنى لي ".
ما لا نفعله نحن الفيزيائيون (على الأقل لم يزعم أحد من معارفي أنهم يفعلون ذلك) ، لذلك لا نتخيل أبعادًا إضافية. إن دماغي محدود تمامًا مثل دماغك ، وعلى الرغم من أن هذا الدماغ يخلق بسهولة صورة ثلاثية الأبعاد للعالم يمكنني التحرك فيه ، لا يمكنني إجباره على تمثيل صورة لعالم رباعي أو خماسي ، مثلك تمامًا. لم يعتمد حياتي على القدرة على تخيل شيء من هذا القبيل ، لذلك ربما ليس من المستغرب أن دماغي لا يتلاءم مع هذا.
بدلاً من ذلك ، أنا (وبالحكم من خلال تبادل الأفكار ، فإن معظم زملائي أيضًا) أقوم بتطوير الحدس بناءً على مجموعة من المقارنات وحيل التصور والحسابات. نحن نحذف الحسابات هنا ، ولكن العديد من المقارنات والحيل ليس من الصعب تفسيرها.
يمكن تعلم الأفكار حول الأبعاد الإضافية على مرحلتين.
- خطوة بسيطة هي تعلم تخيل أو وصف العالم بأبعاد إضافية. أنت تعرف بالفعل عدة طرق للقيام بذلك ، حتى إذا لم تكن على علم بذلك - ويمكنك تعلم المزيد.
- المرحلة الأكثر صعوبة هي معرفة كيفية عمل كل شيء في العالم بأبعاد إضافية. كيفية العمل بإبرة بأربعة أبعاد ، وليس بثلاثة أبعاد ؛ ما إذا كانت الكواكب ستتحرك في مدارات حول الشمس في ستة أبعاد مكانية ؛ ستتشكل البروتونات والذرات؟ هنا سوف تحتاج إلى تعلم حيل غير مألوفة ، تمثل الاختلافات بين عالم واحد أو بعدين فقط وعالم ثلاثي الأبعاد معروف لنا ، والعمل عن طريق القياس.
فلنبدأ بمساعدتك على تخيل العالم بأبعاد إضافية. للقيام بذلك ، تحتاج إلى التفكير في كيفية تمثيل أي بُعد بشكل عام. لنبدأ من البداية.
- عالم بدون أبعاد هو نقطة. يمكن أن يقال عنه القليل الآن ، لكننا سنعود إليه.
- إن العالم أحادي البعد مثير للاهتمام بالفعل.
- في عوالم ثنائية الأبعاد ، تحدث أشياء أكثر إثارة للاهتمام.
- من المهم تجنب الخلط بين الأبعاد المكانية والمعنى الأعم لكلمة "البعد" في اللغة العادية ، وكذلك في الرياضيات والإحصاء.
- ثم ستتبعها أمثلة مختلفة للأبعاد الإضافية ، مع التركيز على ما يعني بالضبط "إضافية" ، وكيف يمكن أن يكون في عالمنا أبعاد لا نعرف عنها شيئًا.
- سندرس أيضًا كيف يمكن تحديد هذه القياسات غير المرئية بالضبط.
عوالم أحادية البعد
إن العالم ذو البعد المكاني هو أبسط بكثير من العالم الذي به ثلاثة ، ولكن هناك شيء فيه يمكن التفكير فيه. على سبيل المثال ، هناك عدة أنواع من العوالم أحادية البعد. ليس لديهم فقط خصائص مشتركة معينة ، ولكن لديهم أيضًا اختلافات مثيرة للاهتمام.
في المثال الأول ، لنأخذ القياس ليس كمفهوم مادي ، ولكن كمفهوم أكثر عمومية. سيساعدك ذلك بعدة طرق ، على سبيل المثال ، في تشتيت حدسك عن المفاهيم الخاطئة الطبيعية حول الأبعاد وكيفية عملها. لنتحدث عن الأرباح السنوية - مقدار الأموال التي يتلقاها الشخص لمدة عام معين. هذا هو بعد الدراسة المناسب تمامًا مثل أي شخص آخر.
قياس الإيرادات
دخلك للسنة الماضية هو رقم معين بعملتك المحلية. يمكن أن تكون إيجابية أو سلبية ، كبيرة أو صغيرة ؛ يمكن تمثيله كنقطة على خط ، كما في الشكل. 1 ، والتي سوف نسميها "نقطة الدخل". تمثل كل نقطة على الخط عودة محتملة.
التين. 1: خط إيرادات بطول لانهائي ، يمثل الجانب الأيسر منه الخسائر ، ويمثل الجانب الأيمن الدخل.ما يجعل الدخل السنوي خاصية ذات بعد واحد هو (تقريبًا جدًا) ما يلي:
• يشار إلى الموقف في الفضاء بوحدة معلومات واحدة: في حالتنا ، حسب الدخل.
لاحظ أيضًا أنه مستمر (أو شبه مستمر) - إذا كان لدى شخصين دخول مختلفة A و B ، فيمكننا العثور على الثلث الذي يكون دخله بين A و B.
تشير هاتان الحقائقان إلى أن الدخل يمكن أن يتغير باستمرار على طول خط الدخل ، والانتقال إلى اليمين أو اليسار - إما إلى دخل أعلى أو أدنى. لا توجد خيارات أخرى.
بالطبع ، لا علاقة لخط الإيرادات بالمساحة المادية التي يمكنك أنت وأنا المشي فيها ، ولكن هذا لا يزال بعدًا. و (على الأقل من حيث المبدأ) ليس له نهاية في أي من الطرفين: لا يوجد (من حيث المبدأ) أي حد على مقدار المال الذي يمكن للشخص أن يكسبه أو يخسره في السنة. هذا العالم أحادي البعد ليس متنوعًا للغاية ، ولكن لا يزال بإمكاننا طرح بعض الأسئلة ذات مغزى حوله:
- كيف يتم توزيع الإيرادات السنوية في الولايات المتحدة؟
- ما هو متوسط الدخل السنوي في اليابان؟
- كيف تتغير الإجابات على هذه الأسئلة بمرور الوقت؟
هذه الأسئلة منطقية في عالم أحادي البعد لخط الإيرادات.
قياس قوس قزح
وهنا عالم آخر مختلف تمامًا. يتكون البُعد الواحد من ألوان قوس قزح ، من الأحمر إلى البرتقالي إلى الأصفر ، ومن هناك إلى الأخضر ، [الأزرق] ، الأزرق والبنفسجي [الناطقون بالإنجليزية ستة ألوان في قوس قزح ، لا ينبعث منها أزرق / تقريبًا. ترجم.]. من وجهة النظر هذه ، تشكل الألوان عالمًا أحادي البعد بحجم محدود. خارج الأحمر أو الأرجواني ، هناك أشكال غير مرئية من الزهور ، ولكن من وجهة نظر عينيك ، ينتهي القياس عليها. الآن لا يتم تقديمه في شكل خط لانهائي ، ولكن في شكل مقطع - "خط قوس قزح" في الشكل. 2. من فضلك لا تخلط بينه وبين عجلة الألوان - إذا كانت مغلقة ، فإن قياسنا يبدأ باللون الأحمر وينتهي باللون الأرجواني. ومرة أخرى ، يتم تحديد الموضع على خط قوس قزح بوحدة معلومات واحدة (اللون) ، وهو مستمر.
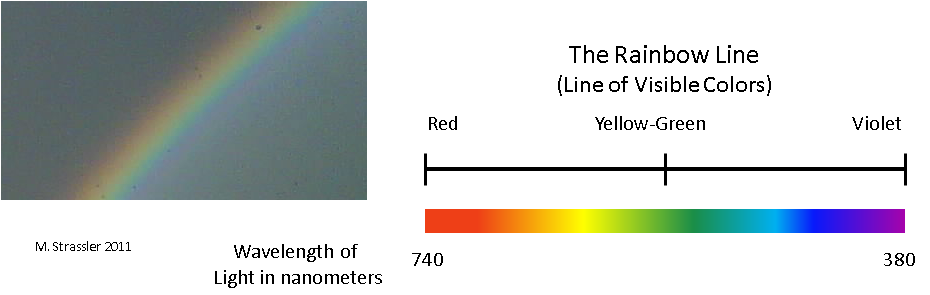التين. 2من الواضح أن هذا ليس أيضًا قياسًا للمساحة المادية! يمكنك رمي كرة من منزلك إلى منزل جارك ، ولكن لا يمكنك أن تتخيل كيف ترمي كرة من اللون الأخضر إلى البرتقالي - فهذا لا معنى له. وستظل بعدًا أيضًا. هنا يمكنك طرح الكثير من الأسئلة ذات المغزى: كيف يتحرك لون التفاح على طول خط قوس قزح في عملية تحويل تفاحة من اللون الأخضر إلى الأحمر؟ كم في ضوء الشمس لكل زهرة؟ إذا بدأ نجم برتقالي في التحول إلى اللون الأحمر ، فهل يتحول إلى اللون الأصفر أولاً؟
قياس اتجاه الرياح
وهنا خيار القياس الثالث ، ومرة أخرى. إذا استمعت لتوقعات الطقس ، فسيتم إخبارك بأن الرياح ستبدأ قريبًا في النفخ من الشمال ، أو من الشمال الغربي ، أو من الجنوب الغربي. اتجاهات الرياح المحتملة هي أيضا قياس. يرجى ملاحظة أن هذا ليس بعدًا مكانيًا! في هذا البعد ، لا يمكنك رمي الكرة بالطريقة التي ترمي بها ، إلى اليسار ، أو إلى الأمام. هذا هو قياس الاتجاهات في الفضاء!
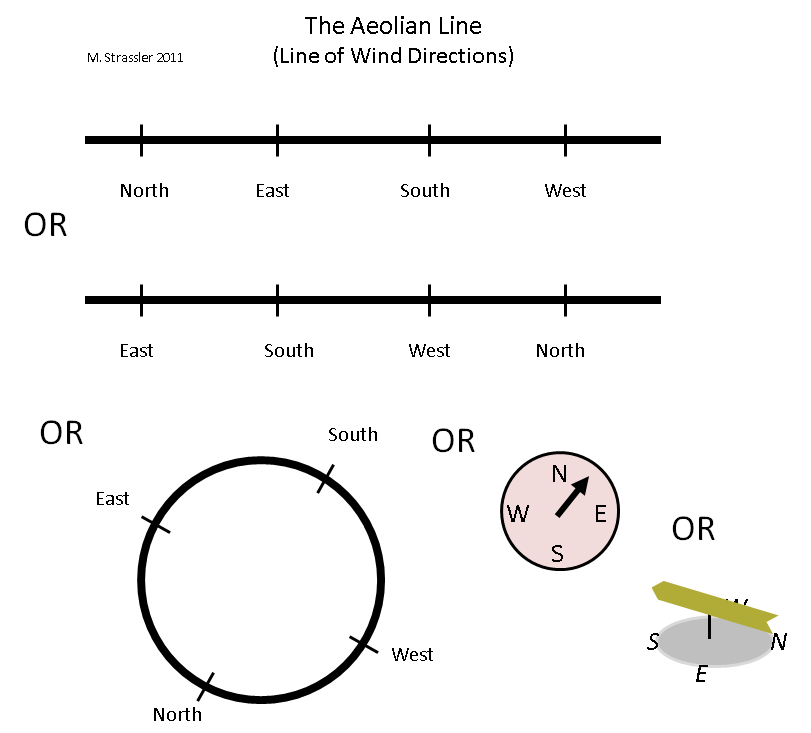التين. 3كيف يمكن تمثيل هذا البعد؟ هناك طريقتان طبيعيتان على الأقل لهذا ، كما هو موضح في الشكل. 3. يستخدم المرء الجزء - "خط إيولايان" (
أيولوس هو أنصاف الآلهة ، وحاكم العناصر الجوية لليونانيين القدماء) - لكن الخط الأيولي يختلف عن خط قوس قزح في تردده. يمكن أن يتغير اتجاه الريح من الشمال إلى الشرق ، ثم إلى الجنوب ، ثم إلى الغرب ، ثم مرة أخرى إلى الشمال باستمرار. ومن وجهة نظرنا ، يمكن قطع الخط في أي مكان - قارن بين الخطين في أعلى الشكل. 3 ، والتي تمثل بشكل جيد الخط الأيولي. خلاصة القول هي أن الرياح يمكن أن تنتقل من الطرف الأيمن للخط مباشرة إلى الطرف الأيسر ، والعكس صحيح ، لذلك لا يهم أين تقطعها. أو ربما أسهل طريقة لتمثيل هذا الخط الدوري هي في شكل دائرة. هذا ما نقوم به مع بوصلة أو ريشة الطقس!
ثلاثة عوالم أحادية البعد مختلفة
وهنا لديك عوالم أحادية البعد. انظر كم هم أثرياء في التفاصيل! أحجام مختلفة وخصائص مختلفة. على خط الدخل ، يمكن أن يزيد الدخل أو ينخفض إلى الأبد. على خط قوس قزح ، يمكن أن تتحرك عينيك فقط إلى اللون الأرجواني ، أو العكس ، إلى اللون الأحمر فقط. وعلى خط إيولايان ، يمكن للرياح أن تشكل دائرة كاملة بقدر ما تريد - ولكن في نفس الوقت ستعود دائمًا إلى أحد الاتجاهات.
هذه الأصناف من عوالم أحادية البعد - لا نهائية ، محدودة ، ودورية محدودة ، ممثلة بخط لا نهائي ، مقطع ودائرة - هي المكونات الأساسية لفهم عوالم ذات أبعاد أعلى. سأتصل بهم أكثر من مرة. في الشكل. 4 يتم تقديمها ، وكذلك النوع الرابع ، وتمتد إلى ما لا نهاية في اتجاه واحد فقط. مثال على هذا القياس يمكن أن يكون درجة الحرارة: يمكن أن يكون كبيرًا بشكل تعسفي ، ولكن هناك أدنى درجة حرارة ممكنة - صفر مطلق - لذا فإن درجة الحرارة تشكل خطًا يبدأ من الصفر المطلق ويصعد من هناك ، ولكن ليس إلى الأسفل.
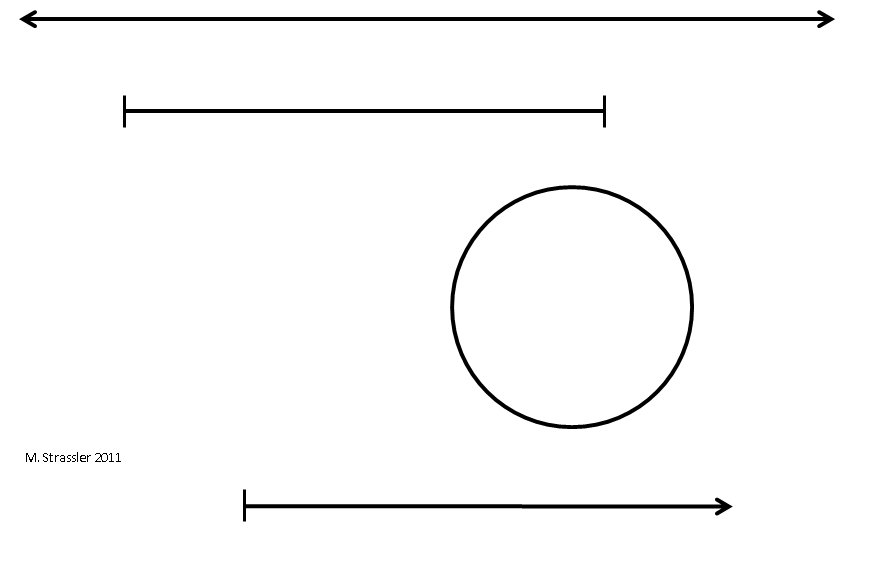التين. 4كيفية تصوير الأبعاد المكانية وغيرها
ذكرت أو عرضت عدة طرق مختلفة لتمثيل القياسات. يمكن تمثيل الدخل برقم أو خط لا نهاية له. يمكن تمثيل قوس قزح المرئي كقطعة ، أو كلون ، وكذلك استخدام عدد - طول موجة الفوتونات المقابلة للون معين. يمكن تمثيل اتجاه الريح بدائرة ، أو مقطع ترتبط نهايته اليسرى باليمين - أو كلمات مثل الشمال أو الشرق أو الجنوب أو الغرب - أو رقم يحدد الاتجاه بالدرجات ، بدءًا من 0 إلى 360 والعودة إلى 0. ما يمكننا تقديم بُعد واحد بعدة طرق مختلفة يمنحنا مرونة هائلة لتدريب العمل البديهي بأبعاد إضافية.
لتوضيح هذه الأنواع من القياسات ، اخترت مفاهيم لا علاقة لها بالفضاء المادي - الدخل ولون قوس قزح واتجاه الرياح - لإظهار أن القياسات المكانية هي أمثلة ملموسة لمفهوم قياس أكثر عمومية. إن فهم هذه الحقيقة يسهل بشكل كبير محاولات تخيل عوالم بأكثر من ثلاثة أبعاد. تذكر ، لقد ذكرت جزئين من عملية التفكير حول الأبعاد الإضافية؟ أولاً ، تعلم تمثيلهم ؛ ثانيًا ، فهم كيف يعمل كل شيء ويعمل فيه. الأبعاد المكانية لها ميزات مرتبطة بكيفية عمل بعض الأشياء فيها ، ولكن ليس مع عرضها.
عوالم مكانية ذات بعد فعال واحد
بالنظر إلى كل هذا ، دعونا نفكر في العوالم المكانية التي نلتقي بها بانتظام بعد واحد فعال. أو ، بشكل أدق ، المواقف التي يتصرف فيها جانب معين من عالمنا كما لو كان للفضاء بعد واحد فقط. ثم نقول أن العالم بالنسبة لبعض المشاركين أو الأشياء يصبح بشكل فعال بعد واحد.
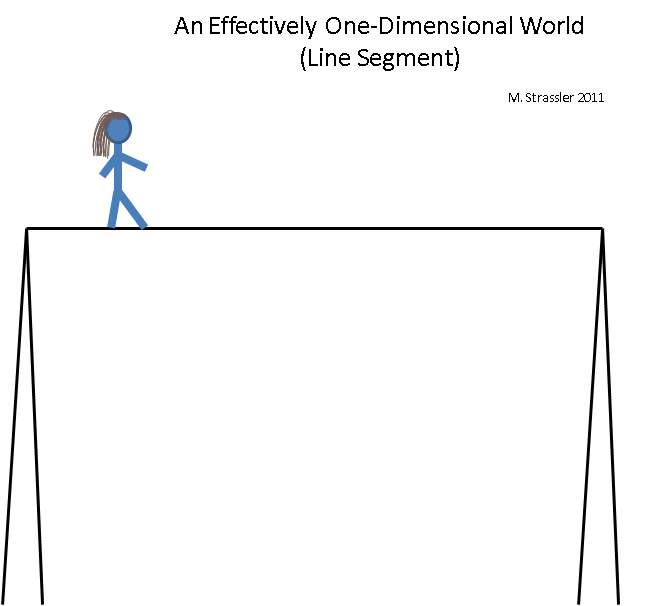التين. 5تخيل أن مشاية حبل مشدود على حبل مرتفع. إن عالم مشاية حبل المشنقة فعال بشكل أحادي البعد (على الرغم من أنه ، بالطبع ، يظل ثلاثي الأبعاد) ، لأنه غير قادر على التحرك بأمان في أي اتجاه بخلاف من اليمين إلى اليسار أو من اليسار إلى اليمين. هذا العالم يشبه عالم قوس قزح - إنه محدود الطول ، وعندما يصل مشاية حبل البهلوان إلى النهاية ، يحتاج إلى الالتفاف والعودة (أو النزول من الحبل ، وإنهاء وضع يصبح فيه العالم فعالًا بعدًا واحدًا). ماذا يمكنني أن أقول؟ يمكن تحديد الموقف على الحبل بوحدة معلومات واحدة (على سبيل المثال ، المسافة من القطب الأيسر إلى مشاية حبل مشدود). يمكن أن يلتقي اثنان من مشاة حبل البهلوان على نفس الخط ، لكنهما لا يمرران بعضهما البعض.
يمكننا تحويل عالم الحبل إلى خط إيولي بإغلاقه في دائرة (الشكل 6). في ذلك ، لا يمكن لاثنين من مشاة حبل مشدود أن يمروا ببعضهم البعض - هذه هي الخاصية الرئيسية للعوالم أحادية البعد. وهذا سيكون البعد النهائي. لكن مشى حبل البهلوان في مثل هذه الحالة يمكن أن يمشي بالفعل في دائرة بشكل مستمر ولانهائي ، دون توقف.
التين. 6عوالم أحادية البعد المعروفة الأخرى (بشكل فعال):
- الطريق الضيق عالم أحادي البعد للسيارات.
- مسار ضيق مع منحدر - لسائح يتسلق جبلًا ؛
- طوابق مبنى شاهق للمصعد.
بشكل عام ، يظل العالم ثلاثي الأبعاد ، ولكن لوصف سيارة أو سائح أو مصعد ، يجب تمثيل بُعد واحد فقط.
تذكر في المستقبل: نحن نعيش في عالم ظاهر ثلاثي الأبعاد ، وكل شيء نلتقي به يبدو لنا ثلاثي الأبعاد. ولكن في بعض الأحيان ، يمكن لعالمنا ثلاثي الأبعاد (بشكل أدق ، جزء منه) أن يتصرف بشكل فعال أحادي البعد ، أو ثنائي الأبعاد (هل يمكنك الخروج بأمثلة؟) أو حتى صفر الأبعاد! (كل شخص سيئ الحظ أن يعلق في ازدحام مروري لا يتحرك في أي مكان يعرف ما هو هذا العالم بدون أبعاد!) هذا الحدس سيكون مفيدًا جدًا لنا لاحقًا.