كشف عالم رياضيات بارز عن تفاصيل كيفية ارتباط نجاحاته في دراسة المشاكل الرياضية القديمة منذ آلاف السنين بالمفاهيم المأخوذة من الفيزياء.
Mignon Kimالرياضيات مليئة بأنظمة الأعداد الغريبة التي لم يسمع بها معظم الناس. بعضها سيكون من الصعب تخيله. لكن
الأرقام العقلانية مألوفة للجميع. هذه أرقام لحساب الأشياء والكسور - جميع الأرقام المعروفة لنا من المدرسة الابتدائية. لكن في الرياضيات ، يصعب أحيانًا فهم أبسط الأشياء. إنها بسيطة ، مثل الجدار الأملس ، بدون شقوق أو نتوءات ، أو خصائص واضحة أخرى يمكنك الإمساك بها.
Minion Kim ، عالم الرياضيات في جامعة أكسفورد ، مهتم بشكل خاص بمسألة أي أرقام منطقية مناسبة لحل معادلات من نوع معين. حفزت هذه المشكلة المتخصصين في نظرية الأعداد لآلاف السنين. وبالكاد حققوا أي تقدم نحو حلها. عندما تتم دراسة السؤال لفترة طويلة وبدون إجابة ، يمكن استنتاج أن الطريقة الوحيدة للتقدم فيه هي طرح فكرة جديدة جذرية. هذا بالضبط ما فعله كيم.
"لا يوجد الكثير من التكنولوجيا الموجودة ، على الرغم من أننا نعمل على ذلك منذ 3000 عام. قال جوردان إلينبرغ ، عالم الرياضيات في جامعة ويسكونسن في ماديسون: "عندما يقدم شخص ما طريقة جديدة حقًا للقيام بذلك ، يكون ذلك مفيدًا للغاية - وقد قام Mignon بذلك تمامًا".
على مدى العقد الماضي ، وصف كيم طريقة جديدة تمامًا للعثور على الأنماط في عالم الأرقام العقلانية المضطرب على ما يبدو. ووصف هذه الطريقة في المقالات والمؤتمرات ، ونقلها إلى الطلاب الذين يواصلون هذا العمل بأنفسهم. لكنه كان ينقذ شيئًا دائمًا. لم تستند رؤيته ، التي أعطت أفكاره للحياة ، على عالم خالص من الأرقام ، ولكن على مفاهيم مستعارة من الفيزياء. بالنسبة لكيم ، فإن القرارات العقلانية تذكرنا إلى حد ما بمسار الضوء.
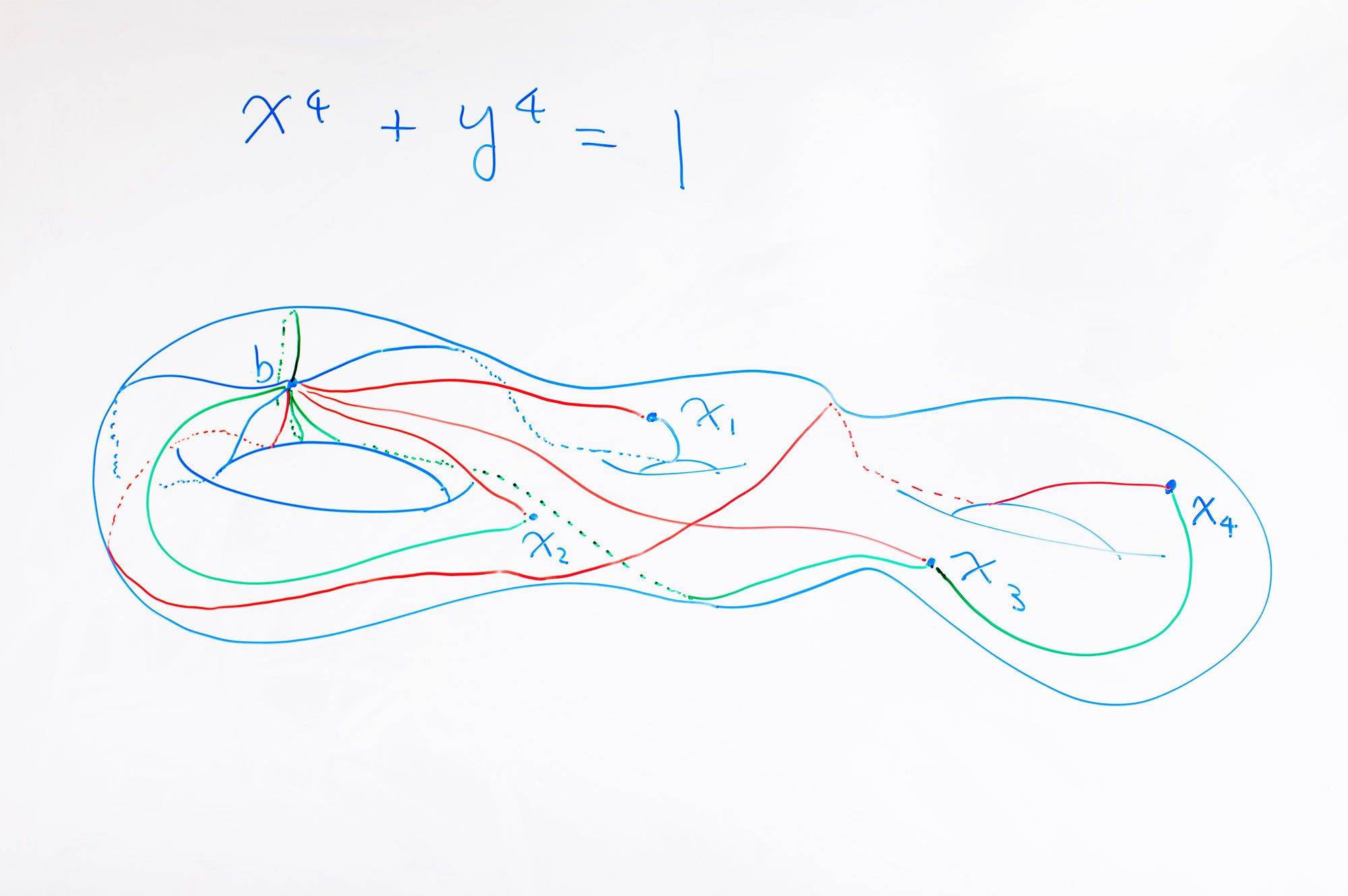يزين جسم كيم في جامعة أكسفورد جسمًا رياضيًا ، وحيد ثلاثي الثقب.إذا كان هذا الاتصال يبدو رائعًا ، فهو كذلك ، حتى بالنسبة للرياضيين. لذلك ، لم تكشف كيم عن تفاصيلها لفترة طويلة. "لقد أخفيتها لأنه لسنوات عديدة كنت مرتبكًا بالعلاقة مع الفيزياء" ، كما يقول. "المتخصصون في نظرية الأعداد هم أشخاص عمليون للغاية ، وتأثير الفيزياء في بعض الأحيان يجعلهم متشككين في الرياضيات".
لكن كيم يقول الآن إنه مستعد لمشاركة رؤيته. "أعتقد أن التغيير هو مجرد عرض للشيخوخة!" - كتب كيم ، الذي بلغ 53 عامًا ، في إحدى الرسائل الأولى التي تبادلناها لكتابة هذه القصة.
عقد مؤخرًا مؤتمرًا جمع خبراء في نظرية الأعداد ونظرية الأوتار. كما رسم مسودات للمقالات بداية لوصف إلهامه للمجتمع الرياضي ، وليس معتادًا على التفكير في الأرقام باستخدام مثل هذه المقارنات المباشرة مع العالم المادي.
لا يزال هناك عقبة واحدة فقط - الجزء الأخير من تشبيه الفيزياء في الرياضيات ، والتي لم يجدها كيم بعد. ويأمل أن يتلقى دعوة من خلال مشاركة الآخرين ، وخاصة الفيزيائيين ، للمساعدة اللازمة لإكمال العمل.
اللغز القديم
تجتذب الحلول العقلانية للمعادلات بنشاط العقل البشري. إنها تجلب الرضا ، على غرار ما تحصل عليه من قطع اللغز التي تناسب مكانها. لذلك ، هم أبطال أشهر الفرضيات الرياضية.
تتضمن الأرقام المنطقية الأعداد الصحيحة وأي رقم يمكن التعبير عنه كنسبة من عددين صحيحين ، على سبيل المثال ، 1 أو -4 أو 99/100. يهتم علماء الرياضيات بشكل خاص بالأرقام العقلانية التي تحل معادلات ديوفانتين - معادلات متعددة الحدود مع معاملات صحيحة ، على سبيل المثال ، س
2 + ص
2 = 1. وقد تم تسميتهم على اسم عالم الرياضيات
ديوفانتوس ، الذي درسها في الإسكندرية في القرن الثالث الميلادي.
يصعب العثور على حلول عقلانية في الحالة العامة ، لأنها لا تطيع أي انتظام هندسي. خذ المعادلة x
2 + y
2 = 1. حلولها
بالأرقام الحقيقية تشكل دائرة. قم بإزالة جميع النقاط في الدائرة التي لا يمكن التعبير عنها على شكل كسور ، وستبقى القرارات العقلانية فقط التي لا تشكل مثل هذا الشيء الأنيق. تبدو الحلول العقلانية متناثرة بشكل عشوائي حول المحيط.
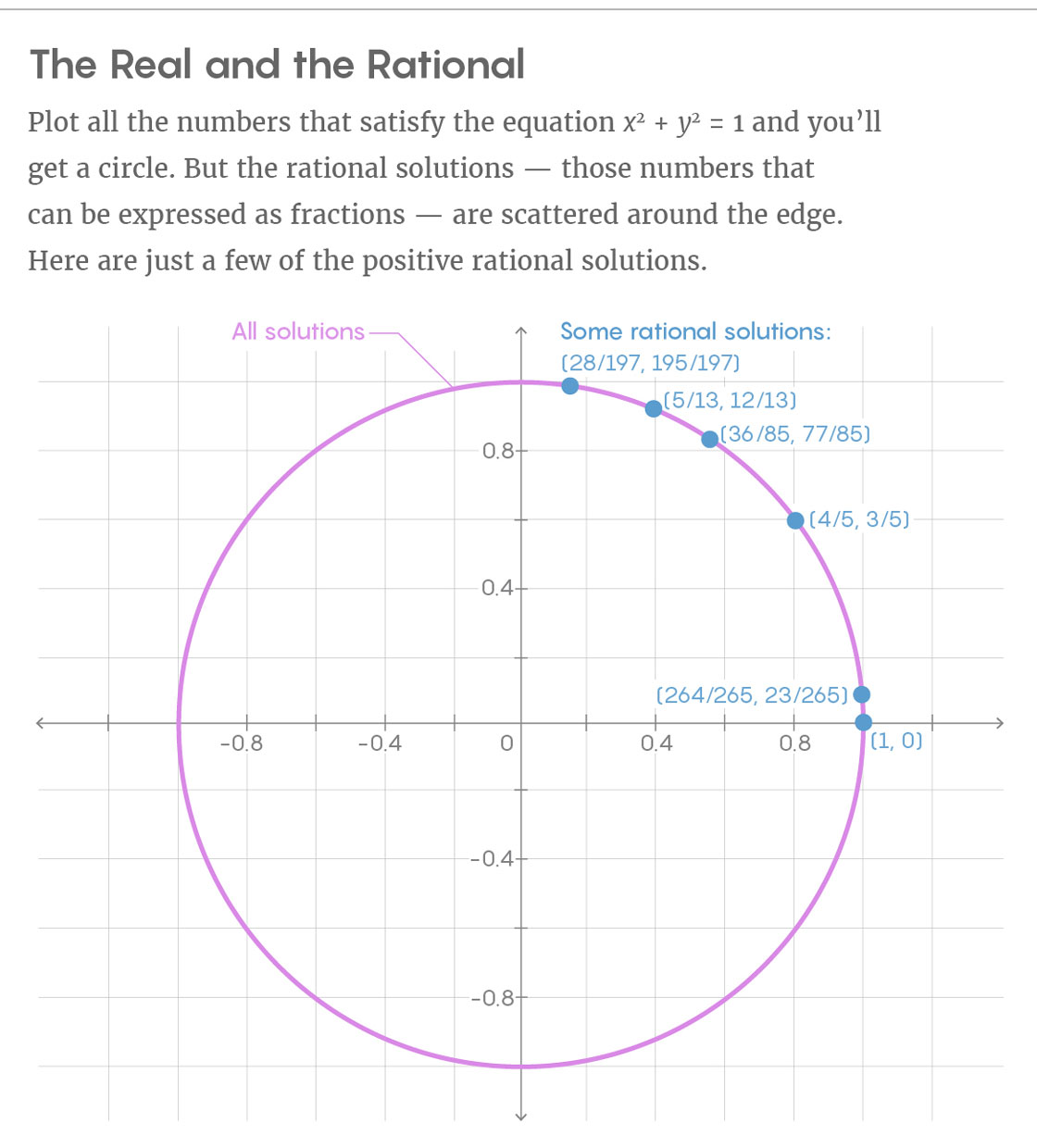
"إن الحالة التي يجب أن تطيعها النقطة من أجل الحصول على إحداثيات عقلانية ليست هندسية على الإطلاق. يقول كيم: من المستحيل كتابة معادلة يجب أن تحققها النقاط العقلانية.
غالبًا ما يكون من السهل جدًا العثور على حل منطقي واحد ، أو حتى عدة حلول. لكن علماء الرياضيات الذين لا يحبون التقليل من شأنهم مهتمون أكثر بإيجاد جميع الحلول العقلانية. وهذا أكثر تعقيدًا. من الصعب جدًا أن تكون الأدلة حتى على بيان بسيط حول عدد القرارات العقلانية كافية لتمريرها في النجم الرياضي. في عام 1986 ، فاز
Gerd Falting بجائزة
Fields Prize ، وهي أعلى جائزة رياضية ، وذلك بشكل رئيسي لإثبات
فرضية Mordell ، التي تنص على أن فئات معينة من معادلات Diophantine ليس لديها سوى عدد محدود من الحلول العقلانية.
كان دليل فالتينغ نقطة تحول في نظرية الأعداد. وأيضاً بما يسميه علماء الرياضيات "دليلاً غير فعال" ، لأنها لم تقدم العدد الدقيق للحلول العقلانية ولم تجدها. منذ ذلك الحين ، كان علماء الرياضيات يبحثون عن طرق للقيام بهذه الخطوات التالية. تبدو النقاط العقلانية عشوائية على الرسم البياني المعادلة العادية. يأمل علماء الرياضيات أنه من خلال تغيير السياق الذي يفكرون فيه في مشكلة ما ، يمكن جعل هذه النقاط تبدو وكأنها مزيج هادف يمكن وصفه بطريقة معينة. المشكلة هي أن مجالات الرياضيات المعروفة لا توفر مثل هذا السياق.
كيم في مكتبه في أكسفوردوقالت إيلينبرغ: "من أجل الحصول على نتائج فعالة من النقاط العقلانية ، هناك حاجة واضحة لفكرة جديدة".
الآن هناك افتراضان رئيسيان حول طبيعة هذه الفكرة. يأتي أحدهم من عالم الرياضيات الياباني
شينيتشي موتيزوكي ، الذي نشر في عام 2012 عملاً
رياضيًا معقدًا ومبتكرًا يضم عدة مئات من الصفحات على صفحة الكلية في جامعة كيوتو. بعد خمس سنوات ، لا يزال هذا العمل غير مفهوم إلى حد كبير. جاءت فكرة جديدة أخرى من كيم ، الذي حاول تخيل أرقام عقلانية في سياق رقمي موسع تبدأ فيه أنماطها المخفية في الظهور.
حل متماثل
غالبًا ما يقول علماء الرياضيات أنه كلما كان الشيء متناظرًا ، كان من الأسهل دراسته. لذلك ، يرغبون في وضع دراسة معادلات ديوفانتين في ظروف تحتوي على مزيد من التناظر من تلك التي تنشأ فيها هذه المشكلة بشكل طبيعي. إذا نجح ذلك ، فسيتمكنون من استخدام التماثلات المكتشفة حديثًا لتتبع النقاط العقلانية التي يحتاجونها.
لفهم كيف يساعد التناظر عالم الرياضيات في التنقل في مشكلة ما ، تخيل دائرة. ربما هدفك هو تحديد جميع النقاط في الدائرة. يساعد التناظر كثيرًا ، لأنه ينشئ خريطة تسمح لك بالانتقال من النقاط التي تعرفها إلى تلك التي لا يزال يتعين اكتشافها.
تخيل أنك وجدت جميع النقاط العقلانية في أسفل الدائرة. نظرًا لأن الدائرة لها تناظر مرآة ، يمكن أن تنعكس النقاط لأعلى (تغيير العلامات في جميع إحداثيات ص) والحصول فجأة على جميع النقاط من الأعلى. تحتوي الدائرة بشكل عام على تناظر غني لدرجة أنه للبحث عن جميع النقاط عليها ، تحتاج إلى معرفة موضع نقطة واحدة فقط ، ثم دمجها مع المعرفة حول تناظر الدائرة: تحتاج فقط إلى تطبيق التناظر اللانهائي للدائرة على نقطة البداية.
ولكن إذا كان الكائن الهندسي الذي تعمل معه أقل دقة بكثير ، على سبيل المثال ، المسار الذي يهز بشكل عشوائي ، فسيتعين عليك العمل كثيرًا لتحديد كل نقطة على حدة - لن تكون لديك علاقات متناظرة تسمح لك بوضع علامة على نقاط غير معروفة عندما مساعدة المشاهير.
يمكن أن تحتوي المجموعات العددية أيضًا على التماثلات ، وكلما زاد التماثل في المجموعة ، أصبح من السهل فهمها - يمكنك تطبيق العلاقات المتماثلة لاكتشاف القيم غير المعروفة. تشكل الأرقام التي تحتوي على أنواع معينة من التماثل "مجموعة" ، ويستخدم علماء الرياضيات خصائص المجموعة لفهم الأرقام الواردة فيها.
العديد من الحلول العقلانية للمعادلة لا يجب أن يكون لها تناظر ولا تشكل مجموعة ، ولهذا السبب يواجه علماء الرياضيات مهمة غير واقعية في محاولة إيجاد حلول واحدة تلو الأخرى.
من الأربعينيات ، بدأ علماء الرياضيات في دراسة طرق ترتيب معادلات ديوفانتين في ظروف أكثر تناسقًا. اكتشف عالم الرياضيات كلود تشابوتي أنه داخل المساحة الهندسية الأكبر التي أنشأها (باستخدام كون موسع من الأرقام تسمى أرقام
p-adic ) ، تشكل الأرقام العقلانية فضاءها الفرعي المتماثل الخاص بها. أخذ هذه المساحة الفرعية
ودمجها مع قطعة من معادلة ديوفانتين. تحولت نقاط تقاطعها إلى حلول عقلانية للمعادلة.
في الثمانينيات ، حدد عالم الرياضيات
روبرت كولمان عمل شابوتي. على مدى العقدين التاليين ، كان نهج كولمان تشابوتي أفضل أداة رياضية كان على علماء الرياضيات إيجاد حلول عقلانية لمعادلات ديوفانتين. لكنه يعمل فقط إذا كان الرسم البياني للمعادلة يرتبط بحجم مساحة أكبر بنسبة معينة. عندما يتم كسرها ، يصبح من الصعب العثور بدقة على موضع نقاط التقاطع في منحنى المعادلة والأرقام العقلانية.
قال كيران كيدلايا ، عالم الرياضيات في جامعة كاليفورنيا ، سان دييغو: "إذا كان المنحنى الخاص بك في بيئة يوجد فيها الكثير من النقاط العقلانية ، فإنه يبدأ في التراكم ويصعب عليك تحديد أي منها موجود على المنحنى".
ثم يدخل كيم. لتوسيع عمل Chaboti ، أراد أن يجد مساحة أكبر لدراسة معادلات Diophantine - مساحة حيث تكون الأرقام العقلانية أكثر تجزؤًا ، مما يسمح لنا بدراسة نقاط التقاطع مع عدد كبير من أنواع معادلات Diophantine.
مساحات المساحات
إذا كنت بحاجة إلى مساحة أكبر وبعض التلميحات حول كيفية استخدام التناظر لتوجيه نفسك فيه ، فستناسبك الفيزياء.
في الحالة العامة ، الفضاء بالمعنى الرياضي هو أي مجموعة من النقاط ذات هيكل هندسي أو طوبولوجي. ألف نقطة متناثرة بالإرادة أم لا ، لا تشكل مساحة - لا ترتبط ببعضها البعض من خلال هيكل. لكن المجال ، وهو منظمة متصلة بالنقاط ، هو بالفعل مساحة. مثل الحيد ، أو مستوى ثنائي الأبعاد ، أو الزمكان رباعي الأبعاد ، حيث نعيش.
بالإضافة إلى ذلك ، هناك المزيد من المساحات الغريبة التي يمكن تخيلها على أنها "مساحات للمساحات". أبسط مثال: لنفترض أن لديك مثلثًا - وهذه مساحة. تخيل الآن مساحة كل المثلثات الممكنة. تمثل كل نقطة فيه مثلثًا معينًا ، ويتم تحديد إحداثيات هذه النقطة بزوايا المثلث الذي يمثله.
غالبًا ما تكون هذه الفكرة مفيدة في الفيزياء. في إطار النظرية النسبية العامة ، يتطور المكان والزمان باستمرار ، ويعتبر الفيزيائيون كل تكوين للمكان والزمان كنقطة في الفضاء لجميع تكوينات الزمكان. تظهر مسافات المساحات أيضًا في المنطقة التي يطلق عليها الفيزيائيون مقياس الثبات ، ويعملون مع الحقول المتراكبة على الفضاء المادي. تصف هذه الحقول كيف تتغير قوى مثل الكهرومغناطيسية والجاذبية عند التحرك في الفضاء. يمكن للمرء أن يتصور أنه في كل نقطة في الفضاء ، يختلف تكوين هذه الحقول قليلاً - وأن جميع هذه التكوينات المختلفة تشكل نقاطًا في "مساحة جميع الحقول" ذات البعد الأعلى.
هذا الفضاء من الحقول من الفيزياء هو تشابه قريب من اقتراح كيم لنظرية الأعداد. لفهم هذا ، تخيل شعاعًا من الضوء. يمثل الفيزيائيون الضوء يتحرك عبر مساحة الحقول الأعلى. في هذه المساحة ، سيتبع الضوء مسارًا يلتزم بمبدأ المقاومة الأقل ويقلل من مقدار الوقت المطلوب للانتقال من النقطة A إلى النقطة B. يفسر هذا المبدأ لماذا ينحني الضوء عند الانتقال من مادة إلى أخرى - مسار منحني يقلل الوقت التكاليف.
تحتوي المساحات الأكبر للمساحات التي تظهر في الفيزياء على تناظر إضافي غير موجود في أي من المساحات التي يمثلونها. تلف هذه التماثلات الانتباه إلى نقاط معينة ، على سبيل المثال ، التركيز على مسار يقلل الوقت. يمكن التأكيد على نفس التماثلات ، التي تم إنشاؤها بطريقة مختلفة وفي سياق مختلف ، في نقاط أخرى - على سبيل المثال ، في النقاط المقابلة للحلول العقلانية للمعادلات.
ربط التماثل بالفيزياء
في نظرية الأعداد ، لا توجد جسيمات يمكن تتبعها ، ولكن لديها شيء مثل الزمكان ، وتوفر طريقة لرسم المسارات وإنشاء مساحة لجميع المسارات الممكنة. من هذه المراسلات الأساسية ، طور كيم مخططات حيث "مشكلة العثور على مسار الضوء وإيجاد حلول عقلانية لمعادلات ديوفانتين وجهان لنفس المشكلة" ، كما أوضح في مؤتمر في الفيزياء الرياضية في هايدلبرغ الأسبوع الماضي.
تشكل حلول معادلات ديوفانتين مساحات - وهي منحنيات تحددها المعادلات. يمكن أن تكون هذه المنحنيات أحادية البعد ، مثل دائرة ، أو متعددة الأبعاد. على سبيل المثال ، إذا قمت ببناء حل معقد لمعادلة ديوفانتين ×
4 + ص
4 = 1 ، فستحصل على حافز بثلاث فتحات. لا تحتوي النقاط العقلانية لمثل هذا الحيد على بنية هندسية - وهذا هو السبب في صعوبة العثور عليها - ولكن يمكن مقارنتها بالنقاط في مساحة متعددة الأبعاد من المساحات التي تمتلك مثل هذا الهيكل.
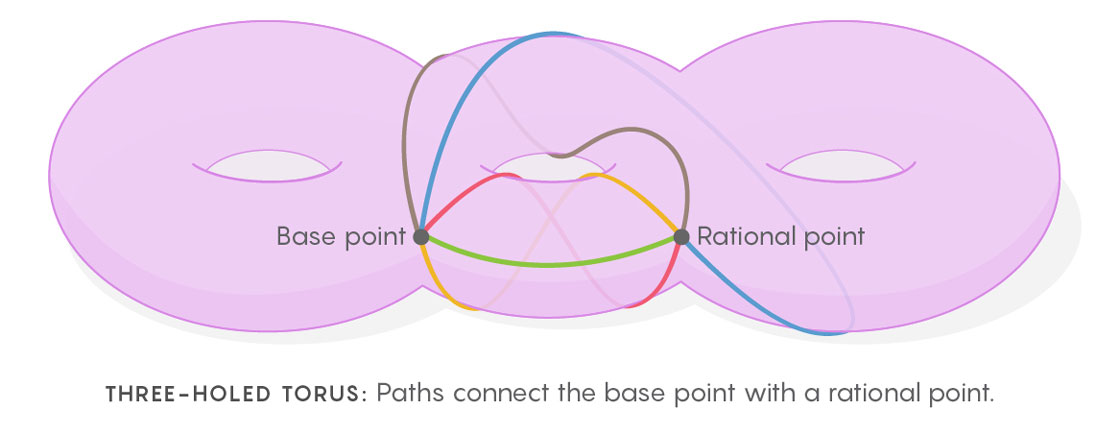
يخلق كيم هذه المساحة متعددة الأبعاد من المساحات ، ويتخيل الطرق التي يمكن من خلالها رسم المنحنيات المغلقة على الحيد (أو في المساحة التي تحدد المعادلة). يبدو إجراء رسم المنحنيات هكذا. تحتاج أولاً إلى تحديد نقطة البداية ، ثم رسم حلقة من هذه النقطة إلى أي نقطة أخرى ، والعودة إلى الأولى. الآن كرر هذه العملية ، ورسم المسارات التي تربط بين نقطة الأساس وجميع النقاط الأخرى للحيد. ستحصل على مجموعة كبيرة من الحلقات الممكنة التي تبدأ وتنتهي عند نقطة الأساس. هذه المجموعة من الحلقات هي كائن مهم مركزيًا في الرياضيات يسمى
المجموعة الأساسية للفضاء.
يمكن استخدام أي نقطة على الحيد كنقطة انطلاق. سيكون لكل نقطة مجموعة فريدة من المسارات المنبثقة عنها. يمكن تمثيل كل مجموعة من مجموعات المسار هذه كنقطة في "فضاء متعدد الأبعاد لجميع مجموعات المسارات" (مثل مساحة جميع المثلثات الممكنة). تشبه مساحة الفضاء هذه هندسيًا إلى حد كبير ما يبنيه علماء الفيزياء في نظرية الثبات في المقياس: الطريقة التي تتغير بها مجموعات المسارات عندما تنتقل من نقطة على torus إلى أخرى تشبه إلى حد كبير كيفية تغير الحقول عندما تنتقل من نقطة إلى أخرى آخر في الفضاء الحقيقي. تحتوي مساحة الفضاء هذه على تناظر إضافي ليس على الحيد نفسه. وعلى الرغم من أن النقاط العقلانية على الحيد ليس لها تناظر ، إذا ذهبنا إلى مساحة جميع مجموعات المسارات ، فيمكننا العثور على التماثلات بين النقاط المرتبطة بالأرقام العقلانية. تحصل على التماثلات التي لم تكن مرئية من قبل.
قال كيم: "أحيانًا أقول أن" التماثل الحسابي الكامن "مشفر في هذه المسارات ، وهو مشابه جدًا للتماثلات الداخلية لنظرية ثبات المقياس".
مثل شابوتي ، يجد كيم حلولًا عقلانية من خلال استكشاف نقاط التقاطع في المساحة الأكبر التي أنشأوها. يستخدم التماثلات في هذه المساحة للوصول إلى نقاط التقاطع. ويأمل في تطوير معادلة تحدد هذه النقاط بدقة.
في السياق المادي ، يمكن للمرء أن يتخيل كل الطرق الممكنة التي يمكن أن يمر بها شعاع من الضوء. هذا هو "الفضاء الخاص بك من جميع المسارات". يهتم الفيزيائيون بالنقاط في هذه المساحة المقابلة للمسارات التي تقلل الوقت. يعتقد كيم أن النقاط التي تتوافق مع كثرة المسارات المنبثقة من النقاط العقلانية لها شيء مثل الخاصية نفسها - أي أن هذه النقاط تقلل من بعض الخصائص التي تحدث عند التفكير في الأشكال الهندسية لمعادلات ديوفانتين. لم يكتشف بعد ما قد تكون هذه الخاصية.
كتب لي في رسالة "ما بدأت أحاول أن أجده" هو مبدأ المقاومة الأقل في سياق رياضي. "لم أجدها بعد ، لكني متأكد من وجودها."
مستقبل غير مؤكد
لقد وصفت على مدى الأشهر القليلة الماضية رؤية كيم ، المستوحاة من الفيزياء ، من قبل العديد من علماء الرياضيات ، والمعجبين بمساهماته في نظرية الأعداد. ولكن عند معرفة مثل هذه التفاصيل من عمله ، فقدوا.
"كمنظّر للكميات التمثيلية ، إذا عرضت علي كل تلك الإنجازات المدهشة التي حققها المينيون وسألت عما إذا كانت مستوحاة من الفيزياء ، لقلت: ما الذي تتحدث عنه بحق الجحيم؟" - قال الينبرغ.
حتى الآن ، لم يذكر كيم الفيزياء في أي من أعماله. وبدلاً من ذلك ، يكتب عن أشياء تسمى "اختلافات سلمر" ، ويفحص العلاقة بين اختلافات سلمر في مساحة جميع اختلافات سلمر. هذه الأشياء مألوفة لخبراء نظرية الأعداد. لكن بالنسبة لكيم ، كانت دائمًا مجرد تسمية أخرى لأشياء مادية معينة.قال كيم: "يجب أن تكون هناك طريقة لاستخدام الأفكار المادية لحل المشكلات في نظرية الأعداد ، لكننا لم نفكر بعد بما يكفي في كيفية إنشاء مثل هذه المنصة". "نحن في حالة حيث تطور فهمنا للفيزياء جيدًا ، ويهتم به الكثير من المتخصصين في نظرية الأعداد من أجل اتخاذ الخطوة التالية."العقبة الرئيسية التي تعترض طريقة كيم هي في العثور على بعض الإجراءات لتقليل مساحة جميع مجموعات الحلقات. في العالم المادي ، يبدو هذا النهج طبيعيًا ، ولكن في الحساب ليس له معنى واضح. حتى علماء الرياضيات الذين يراقبون عمل كيم عن كثب ليسوا متأكدين مما إذا كان بإمكانه العثور عليه."أعتقد أن برنامج كيم سيقدم لنا الكثير من الأشياء الرائعة. يقول أرناف تريباثي ، أستاذ الفيزياء الرياضية في جامعة هارفارد: "لا أعتقد أننا سنكون واضحين كما يريد مينون أن يفهم ما إذا كانت النقاط العقلانية هي حلول كلاسيكية لنظرية المقياس الحسابي".اليوم ، لا تتقاطع لغة الفيزياء تقريبًا مع ممارسة نظرية الأعداد. يعتقد كيم أن هذا سيتغير بالتأكيد. قبل أربعين عامًا ، كان هناك القليل من القواسم المشتركة بين الفيزياء والهندسة والطبولوجيا. ثم في الثمانينيات ، وجد العديد من علماء الرياضيات والفيزيائيين ، الذين أصبحوا الآن شخصيات مهمة ، طرقًا دقيقة لاستخدام الفيزياء لدراسة خصائص الأشكال. بعد هذا التطور ، تغير هذا المجال ولم يعد إلى الأساليب السابقة.في الوقت الحاضر ، من المستحيل عمليًا أن تكون مهتمًا بالهندسة والطبولوجيا دون معرفة أي شيء عن الفيزياء. قال كيم أنا واثق من أن هذا سيحدث مع نظرية الأعداد أيضًا "في السنوات الـ 15 المقبلة. "جميع الاتصالات طبيعية للغاية."