... وتعلم العمل باستخدام أدوات مطوري Ethereum باستخدام مثال واقعي.
الجزء صفر: ظهر الكائن
لقد أنهيت للتو محاضراتي حول الدورة الكاملة لتطوير التطبيقات اللامركزية القائمة على Ethereum في Solidity باللغة الصينية. أعطيتها في وقت فراغي من أجل زيادة مستوى المعرفة حول blockchain والعقود الذكية بين المجتمع الصيني للمطورين. خلال عملي ، قمت بتكوين صداقات مع اثنين من الطلاب.
وفقط في نهاية الدورة ، وجدنا أنفسنا فجأة محاطين بهذه المخلوقات:
صورة من cryptokitties.coمثل معظم الأشخاص الذين واجهوا هذه الظاهرة ، لم نتمكن أيضًا من مقاومة هذه العمليات المشفرة اللطيفة وسرعان ما أصبحنا مدمنين على اللعبة. لقد أحببنا أن نخرج قططًا جديدة واستبدلنا
طريقة البطة بطريقة القطط المشفرة . أعتقد أن الإدمان على الألعاب سيئ ، ولكن ليس في هذه الحالة ، لأن شغف تربية القطط قادنا بسرعة إلى السؤال:
كيف تحصل قطط التشفير على مجموعة جيناتها؟
قررنا تكريس مساء السبت لإيجاد الإجابة عليه ، ونعتقد أننا تمكنا من إحراز بعض التقدم في تطوير البرمجيات التي تسمح لنا بتحديد الطفرة الجينية لقطط التشفير حديثة الولادة قبل ولادتها. بعبارة أخرى ، يمكن أن يساعدك هذا البرنامج في تحديد وتحديد الوقت المناسب لإخصاب أم القطة ، وبالتالي الحصول على أكثر الطفرات الممكنة إثارة.
نحن ننشر هذه المادة على أمل أن تخدم الجميع كمقالة تمهيدية للتعرف على أدوات تطوير Ethereum المفيدة للغاية ، تمامًا كما سمحت القطط المشفرة نفسها للعديد من الأشخاص غير المعتادين على blockchain بالانضمام إلى صفوف مستخدمي العملة المشفرة.
الجزء الأول: المنطق رفيع المستوى لتوليد القطط الصغيرة
بادئ ذي بدء ، سألنا أنفسنا: كيف هي ولادة قطط التشفير؟
للإجابة على هذا السؤال ، استخدمنا موصل Etherscan blockchain الممتاز ، والذي يسمح لنا بالقيام بأكثر من مجرد "دراسة معلمات ومحتويات الكتل". لذلك اكتشفنا شفرة المصدر لعقد CryptoKittiesCore:
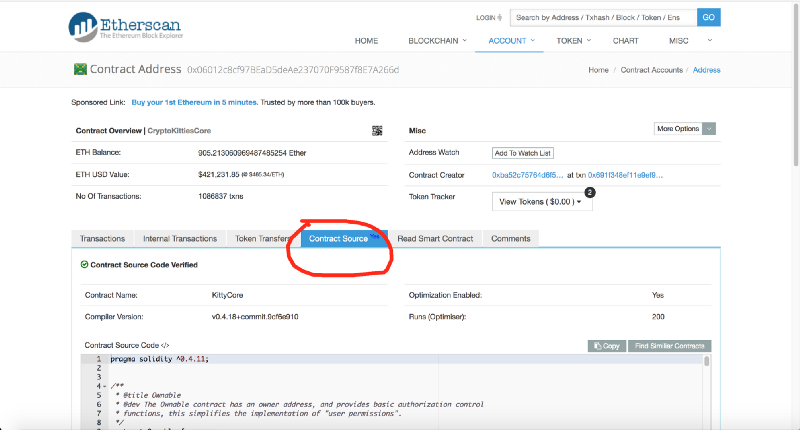https://etherscan.io/address/0x06012c8cf97bead5deae237070f9587f8e7a266d#codeيرجى ملاحظة أن العقد الموسع يختلف في الواقع قليلاً عن ذلك المستخدم في برنامج المكافآت. وفقًا لهذا الرمز ، يتم تشكيل قط صغير في خطوتين: 1) يتم تخصيب القطة الأم بواسطة القطة ؛ 2) بعد ذلك بقليل ، عندما تنتهي فترة نضج الجنين ، يتم استدعاء وظيفة GiveBirth. عادة ما يتم استدعاء هذه الوظيفة من قبل شيطان عملية معين ، ولكن ، كما سترى لاحقًا ، للحصول على طفرات مثيرة للاهتمام ، ستحتاج إلى تحديد الكتلة التي ولدت فيها قطتك بشكل صحيح.
function giveBirth(uint256 _matronId) external whenNotPaused returns(uint256) { Kitty storage matron = kitties[_matronId];
في الكود أعلاه ، يمكنك أن ترى بوضوح أن جينات القط الصغير حديث الولادة يتم تحديدها في وقت الولادة مباشرة عن طريق استدعاء وظيفة mixGenes من العقد الذكي الخارجي geneScience. تأخذ هذه الوظيفة ثلاث معلمات: الجين الأم ، والجين الأب ورقم الكتلة الذي ستكون فيه القطة جاهزة للولادة.
ربما سيكون لديك سؤال منطقي ، لماذا لم يتم تحديد الجينات في وقت الحمل ، كما هو الحال في العالم الحقيقي؟ كما سترى في سياق السرد اللاحق ، يسمح لك هذا بالدفاع بأناقة من محاولات التنبؤ وفك تشفير الجينات. يلغي هذا النهج إمكانية التنبؤ الدقيق بنسبة 100 ٪ لجينات القطط قبل تسجيل حقيقة حمل أم القطة في blockchain. وحتى إذا تمكنت من معرفة الرمز الدقيق المسؤول عن خلط الجينات ، فإن هذا لن يمنحك أي ميزة.
كن على هذا النحو ، في البداية لم نكن نعرف هذا حتى الآن ، لذلك دعونا نستمر. الآن نحن بحاجة لمعرفة عنوان عقد علم الجينات. للقيام بذلك ، استخدم MyEtherWallet:
عنوان عقد GeneScienceهذا ما يبدو عليه رمز بايت العقد:
0x60606040526004361061006c5763ffffffff7c01000000000000000000000000000000000000000000000000000000006000350416630d9f5aed81146100715780631597ee441461009f57806354c15b82146100ee57806361a769001461011557806377a74a201461017e575b600080fd5b341561007c57600080fd5b61008d6004356024356044356101cd565b604051908152602001604051809........
بمظهره ، لا يمكنك القول أنه نتيجة لذلك ، يظهر شيء لطيف مثل القطط على كل شيء ، لكننا محظوظون جدًا لأن هذا عنوان عام ، ولا نحتاج إلى البحث عنه في المستودع). في الواقع ، نعتقد أنه لا ينبغي أن يكون من السهل الوصول إليها. إذا أراد المطورون حقًا التأكد من صحة عنوان العقد ، فيجب عليهم استخدام وظيفة checkScienceAddress ، لكننا لن نتضايق.
الجزء الثاني: انهيار فرضية بسيطة
إذن ما الذي نريد تحقيقه في النهاية؟ يجب أن نفهم أننا لا نضع لأنفسنا هدف تجميع الرمز الفرعي بالكامل ، وتحويله إلى رمز صلابة يمكن للمستخدم قراءته. نحن بحاجة إلى طريقة رخيصة (دون الحاجة إلى الدفع مقابل المعاملات في blockchain القتالية) لتحديد جينات القطط ، شريطة أن نعرف من والديه. هذا ما سنفعله.
للبدء ، دعنا نستخدم
أداة شفرة Etherscan لإجراء تحليل سريع. يبدو هذا:
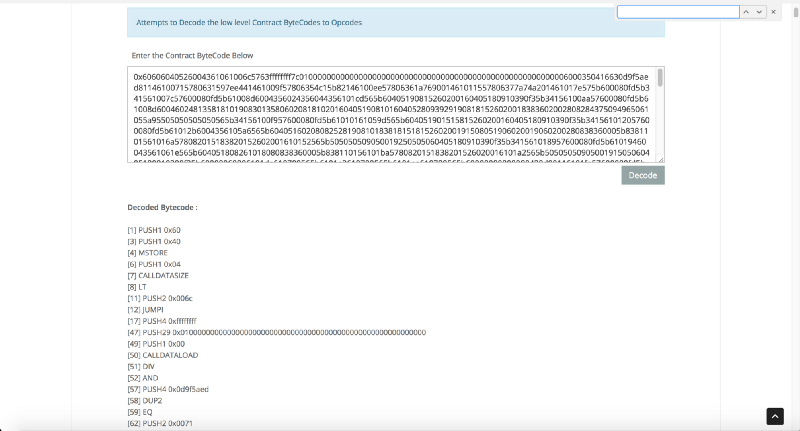أكثر وضوحانحن نتبع القاعدة الذهبية لفك شفرة كود المجمع: نبدأ بفرضية بسيطة وجريئة حول سلوك البرنامج ، وبدلاً من محاولة فهم عمله ككل ، نركز على تأكيد الافتراض. سنستعرض الرمز الثانوي للإجابة على بعض الأسئلة:
- هل تستخدم الطوابع الزمنية؟ لا ، لأن رمز تشغيل TIMESTAMP مفقود. إذا كان هناك أي حادث بسيط فيه ، فإن مصدره هو بالتأكيد رمز تشغيل آخر.
- هل يستخدم تجزئة الكتلة؟ نعم ، يحدث BLOCKHASH مرتين. لذلك ، قد تنشأ العشوائية ، إن وجدت ، من شفراتها ، لكننا لسنا متأكدين من ذلك بعد.
- هل يتم استخدام أي تجزئات على الإطلاق؟ نعم ، يوجد SHA3. ومع ذلك ، ليس من الواضح ما يفعله.
- هل يستخدم msg.sender؟ لا ، لأن رمز تشغيل CALLER مفقود. لذلك ، لا يتم تطبيق تحكم بالوصول على العقد.
- هل يتم استخدام أي عقد خارجي؟ لا ، ليس هناك كود تشغيل CALL.
- هل يتم استخدام COINBASE؟ لا ، وبالتالي نستبعد مصدرًا آخر ممكنًا للعشوائية.
بعد تلقي الإجابة على هذه الأسئلة ، طرحنا وننوي اختبار فرضية بسيطة: يتم تحديد نتيجة mixGene من خلال ثلاث وثلاث معلمات إدخال فقط لهذه الوظيفة. إذا كان الأمر كذلك ، فيمكننا ببساطة نشر هذا العقد محليًا ، والاستمرار في استدعاء هذه الوظيفة مع المعلمات التي تهمنا ، ومن ثم ، ربما يمكننا الحصول على مجموعة من جينات القطط حتى قبل إخصاب القطة الأم.
للتحقق من هذا الافتراض ، نسمي وظيفة mixGene على الشبكة الرئيسية بثلاث معلمات عشوائية: 1111115 ، 80 ، 40 والحصول على بعض النتائج X. بعد ذلك ، قم بنشر هذا
الرمز الفرعي باستخدام
الكمأة و testrpc . لذلك أدى كسلنا إلى طريقة غير قياسية إلى حد ما في استخدام الكمأة.
contract GeneScienceSkeleton { function mixGenes(uint256 genes1, uint256 genes2, uint256 targetBlock) public returns (uint256) {} }
نبدأ بهيكل العقد ، ونضعه في هيكل المجلد الخاص بإطار الكمأة وننفذ مجموعة الكمأة. ومع ذلك ، بدلاً من ترحيل هذا العقد الفارغ مباشرةً إلى testrpc ، فإننا نستبدل رمز بايت العقد في مجلد البناء بالكود البايت الموسع الحقيقي ورمز بايت عقد geneScience. هذه طريقة غير نمطية ولكنها سريعة إذا كنت ترغب في نشر عقد برمز بايت فقط وبعض الواجهة المفتوحة المحدودة للاختبار المحلي. بعد ذلك ، نتصل مباشرة بـ Mixgenes مع المعلمات 1111115 ، 80 ، 40 ، وللأسف نتلقى خطأً في الرد على الرد. حسنًا ، انظر أعمق. كما نعلم ، فإن توقيع وظائف mixGene هو 0x0d9f5aed ، لذلك نأخذ قلمًا وورقة ونتتبع تنفيذ الرمز الثانوي ، بدءًا من نقطة دخول هذه الوظيفة لمراعاة التغييرات في المكدس والتخزين. بعد بضع جامب نجد أنفسنا هنا:
[497] DUP1 [498] NUMBER [499] DUP14 [500] SWAP1 [501] GT [504] PUSH2 0x01fe [505] JUMPI [507] PUSH1 0x00 [508] DUP1 [509] 'fd'(Unknown Opcode)
إذا حكمنا من خلال محتويات هذه السطور ، إذا كان رقم الكتلة الحالية أقل من المعلمة الثالثة ، فسيتم استدعاء (). حسنًا ، هذا سلوك معقول تمامًا: استدعاء وظيفة حقيقية في لعبة برقم كتلة من المستقبل أمر مستحيل وهذا منطقي.
من السهل التحايل على التحقق من الإدخال هذا: فنحن نقوم فقط بإزالة بضع كتل على testrpc واستدعاء الوظيفة مرة أخرى. هذه المرة ، ترجع الدالة Y بنجاح.
لكن للأسف X! = Y
سيء للغاية. هذا يعني أن نتيجة تنفيذ الوظيفة لا تعتمد فقط على معلمات الإدخال ، ولكن أيضًا على حالة blockchain في الشبكة الرئيسية ، والتي تختلف بالطبع عن حالة اختبار blockchain المزيف.
الجزء الثالث: نشمر عن سواعدنا ونحفر في المكدس
حسنًا. لذا فقد حان الوقت لتشمر عن سواعدك. لم يعد الورق مناسبًا لتتبع حالة المكدس. لذلك من أجل عمل أكثر جدية ، سنطلق أداة تفكيك EVM مفيدة للغاية تسمى
evmdis .
بالمقارنة مع الورق والقلم ، فإن هذه خطوة ملموسة إلى الأمام. دعونا نواصل ما توقفنا عنه في الفصل الأخير. ما يلي هو استنتاج مشجع مع evmdis:
............. :label22 # Stack: [@0x70E @0x70E @0x70E 0x0 0x0 0x0 @0x88 @0x85 @0x82 :label3 @0x34] 0x1EB PUSH(0x0) 0x1ED DUP1 0x1EE DUP1 0x1EF DUP1 0x1F0 DUP1 0x1F1 DUP1 0x1F3 DUP13 0x1F9 JUMPI(:label23, NUMBER() > POP()) # Stack: [0x0 0x0 0x0 0x0 0x0 0x0 @0x70E @0x70E @0x70E 0x0 0x0 0x0 @0x88 @0x85 @0x82 :label3 @0x34] 0x1FA PUSH(0x0) 0x1FC DUP1 0x1FD REVERT() :label23 # Stack: [0x0 0x0 0x0 0x0 0x0 0x0 @0x70E @0x70E @0x70E 0x0 0x0 0x0 @0x88 @0x85 @0x82 :label3 @0x34] 0x1FF DUP13 0x200 PUSH(BLOCKHASH(POP())) 0x201 SWAP11 0x202 POP() 0x203 DUP11 0x209 JUMPI(:label25, !!POP()) # Stack: [0x0 0x0 0x0 0x0 0x0 0x0 @0x70E @0x70E @0x70E 0x0 @0x200 0x0 @0x88 @0x85 @0x82 :label3 @0x34] 0x20C DUP13 0x213 PUSH((NUMBER() & ~0xFF) + (POP() & 0xFF)) 0x214 SWAP13 0x215 POP() 0x217 DUP13 0x21E JUMPI(:label24, !!(POP() < NUMBER())) # Stack: [0x0 0x0 0x0 0x0 0x0 0x0 @0x70E @0x70E @0x70E 0x0 @0x200 0x0 @0x213 @0x85 @0x82 :label3 @0x34] 0x222 DUP13 0x223 PUSH(POP() - 0x100) 0x224 SWAP13 0x225 POP() :label24 # Stack: [0x0 0x0 0x0 0x0 0x0 0x0 @0x70E @0x70E @0x70E 0x0 @0x200 0x0 [@0x223 | @0x213] @0x85 @0x82 :label3 @0x34] 0x227 DUP13 0x228 PUSH(BLOCKHASH(POP())) 0x229 SWAP11 0x22A POP() :label25 # Stack: [0x0 0x0 0x0 0x0 0x0 0x0 @0x70E @0x70E @0x70E 0x0 [@0x200 | @0x228] 0x0 [@0x88 | @0x223 | @0x213] @0x85 @0x82 :label3 @0x34] 0x22C DUP11 0x22D DUP16 0x22E DUP16 ...........
ما هو جيد evmdis هو فائدته لتحليل JUMPDEST في التسميات الصحيحة ، والتي لا يمكن المبالغة فيها.
لذا ، بعد أن نجتاز المطلب الأولي ، نجد أنفسنا على الملصق 23. نرى DUP13 ونتذكر من الفصل السابق أن الرقم 13 على المكدس هو معلمتنا الثالثة. لذلك نحن نحاول الحصول على BLOCKHASH من معلمتنا الثالثة. ومع ذلك ، فإن عمل BLOCKHASH يقتصر على 256 كتلة. هذا هو السبب في أنه يتبعه JUMPI (هذا هو بناء إذا). إذا ترجمنا منطق الشفرات إلى لغة الشفرة الزائفة ، نحصل على شيء مثل هذا:
func blockhash(p) { if (currentBlockNumber - p < 256) return hash(p); return 0; } var bhash = blockhash(thrid); if (bhash == 0) { thirdProjection = (currentBlockNumber & ~0xff) + (thridParam & 0xff); if (thirdProjection > currentBlockNumber) { thirdProjection -= 256; } thirdParam = thirdProjection; bhash = blockhash(thirdProjection); } label 25 and beyond ..... some more stuff related to thirdParam and bhash
المزيد من الأشياء المتعلقة بثالث بارام و بهاش - كود آخر يتعلق بثالث بارام و تجزئة الكتلة
الآن نعتقد أننا وجدنا سببًا يميز نتائجنا عن تلك التي نلاحظها في الشبكة الرئيسية. الأهم من ذلك ، يبدو أننا تمكنا من اكتشاف مصدر الصدفة. وهي: يتم حساب تجزئة الكتلة على أساس المعلمة الثالثة ، أو
توقعات المعلمة الثالثة. من المهم ملاحظة أنه في المكدس ، يتم أيضًا استبدال المعلمة الثالثة برقم الكتلة المتوقع هذا.
من الواضح أنه خلال التنفيذ المحلي خارج الشبكة الرئيسية ، ليس لدينا خيار بسيط لفرض عودة BLOCKHASH تتطابق مع قيم الشبكة الرئيسية. كن على هذا النحو ، نظرًا لأننا نعرف جميع المعلمات الثلاث ، يمكننا بسهولة مراقبة الشبكة الرئيسية والحصول على تجزئة الكتلة H للمعلمة الثالثة ، بالإضافة إلى تجزئة الكتلة المتوقعة.
بعد ذلك ، يمكننا إدراج هذه التجزئة مباشرة في رمز البايت في بيئة الاختبار المحلية الخاصة بنا ، وإذا سارت الأمور وفقًا للخطة ، فسوف نحصل في النهاية على المجموعة الصحيحة من الجينات.
ولكن هناك مشكلة واحدة: DUP13 و BLOCKHASH ليست سوى 2 بايت في التعليمات البرمجية ، وإذا استبدلناها فقط بـ 33 بايت PUSH32 0x * التجزئة * ، فسوف يتغير عداد البرنامج تمامًا وسيتعين علينا إصلاح كل من JUMP و JUMPI. أو سيتعين علينا عمل JUMP في نهاية الكود واستبدال التعليمات الخاصة بالكود المنشور ، وهكذا.
حسنًا ، نظرًا لأننا وصلنا إلى هذا الحد ، فسنعثر أكثر قليلاً. نظرًا لأننا ندفع تجزئة 32 بايت غير صفري إلى فرع if ، فسيكون الشرط دائمًا صحيحًا ، وبالتالي ، يمكن التخلص من كل شيء مكتوب في الجزء الآخر لإفساح المجال لتجزئة 32 بايت. حسنًا ، بشكل عام ، هذا ما فعلناه:
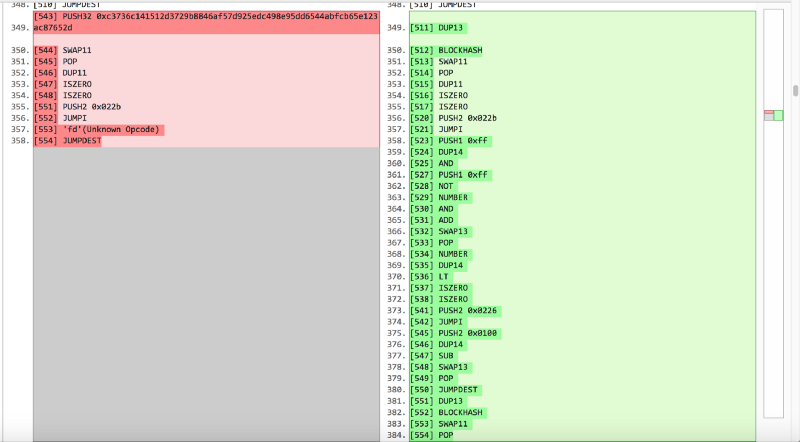
النقطة الأساسية هي أنه نظرًا لأننا تخلينا عن الجزء الآخر من الشرط ، فإننا بحاجة إلى استبدال معلمة الإدخال الثالثة للدالة mixGene بتنبؤات المعلمة الثالثة قبل استدعاؤها.
هذا إلى حد أنه إذا كنت تحاول الحصول على نتيجة عملية
mixGene (X، Y، Z) ، حيث currentBlockNumber هو Z <256 ، ما عليك سوى استبدال تجزئة PUSH32 بتجزئة كتلة Z.
ومع ذلك ، إذا كنت تنوي القيام بما يلي
mixGene (X، Y، Z) ، حيث currentBlockNumber هو Z ≥ 256 ، ستحتاج إلى استبدال تجزئة PUSH32 بتجزئة كتلة proj_Z ، حيث يتم تعريف proj_Z على النحو التالي:
proj_Z = (currentBlockNumber & ~0xff) + (Z & 0xff); if (proj_Z > currentBlockNumber) { proj_Z -= 256; } <b> Z proj_Z , mixGene(X, Y, proj_Z).</b>
لاحظ أن proj_Z سيبقى دون تغيير في نطاق معين من الكتل. على سبيل المثال ، إذا كانت Z & 0xff = 128 ، فعندئذٍ يتغير proj_Z فقط على كل كتلة صفر و 128.
لتأكيد هذه الفرضية والتحقق مما إذا كانت هناك أي مخاطر في المستقبل ، قمنا بتغيير
الرمز الثانوي واستخدمنا أداة مساعدة رائعة أخرى تسمى
hevm .
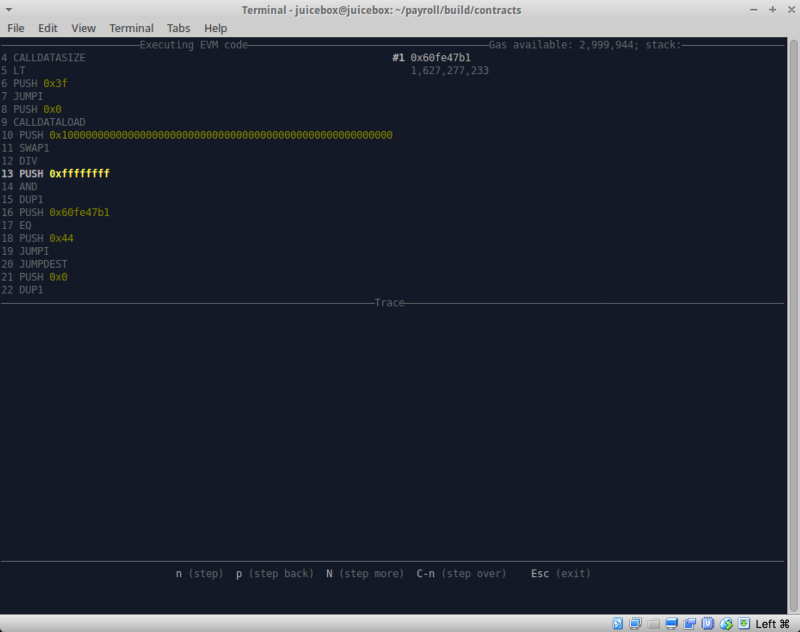
إذا لم تستخدم hevm من قبل ، أوصيك بتجربته. تتوفر الأداة جنبًا إلى جنب مع إطارها الخاص ، ولكن الأهم من ذلك كله في مجموعتها أنه يجب الإشارة إلى شيء مفيد لا غنى عنه مثل مصحح المكدس التفاعلي.
Usage: hevm exec --code TEXT [--calldata TEXT] [--address ADDR] [--caller ADDR] [--origin ADDR] [--coinbase ADDR] [--value W256] [--gas W256] [--number W256] [--timestamp W256] [--gaslimit W256] [--gasprice W256] [--difficulty W256] [--debug] [--state STRING] Available options: -h,--help
أعلاه هي خيارات الإطلاق. الأداة تسمح لك بتحديد مجموعة متنوعة من المعلمات. من بينها - تصحيح الأخطاء ، الذي يمنحك القدرة على التصحيح بشكل تفاعلي.
لذا ، قمنا هنا بعدة مكالمات لعقد علم الجينات المنشور على blockchain الشبكة الرئيسية وسجلنا النتائج. ثم استخدمنا صيغة hevm لتشغيل كود البايت المكسور الخاص بنا مع البيانات المعدة مع مراعاة القواعد الموضحة أعلاه و ...
النتائج هي نفسها!
الفصل الأخير: ختام واستمرار العمل (؟)
إذن ما الذي تمكنا من تحقيقه؟
باستخدام برنامج الاختراق الخاص بنا ، يمكنك فرصة 100٪ للتنبؤ بجين 256 بت لقط صغير حديثي الولادة إذا ولد في نطاق الكتل [coolDownEndBlock (عندما يكون الطفل جاهزًا للظهور) ، الكتلة الحالية هي + 256 (تقريبًا)]. يمكنك التفكير في ذلك على النحو التالي: عندما يكون الطفل في رحم القطة الأم ، تتحول جيناتها بمرور الوقت ، بسبب مصدر الكون في شكل تجزئة كتلة coolDownEndBlock المتوقعة ، والتي تتغير أيضًا بمرور الوقت. لذلك ، يمكنك استخدام هذا البرنامج للتحقق من كيفية ظهور جين الطفل إذا كان قد ولد في الوقت الحالي. وإذا كنت لا تحب هذا الجين ، يمكنك الانتظار حوالي 256 كتلة أخرى (في المتوسط) والتحقق من الجين الجديد.
قد يقول شخص ما أن هذا ليس كافيًا ، حيث يمكن اعتبار دقة التنبؤ بنسبة 100 ٪ فقط قرصنة مثالية حتى قبل حمل قطة الأم. ومع ذلك ، هذا غير ممكن ، لأن جين القط لا يتم تحديده فقط من خلال جينات والديه ، ولكن أيضًا من خلال التجزئة المتوقعة للكتلة كعامل طفرة ، والذي لا يمكن ببساطة معرفته قبل الإخصاب.
ما الذي يمكن تحسينه وما هي الفروق الدقيقة هنا؟
استعرضنا بسرعة التغييرات التي تحدث على المكدس في الجزء المنطقي الحقيقي من العقد الذكي (التسمية 25 وكل شيء بعده) ونعتقد أن هذا الجزء الذي يمكن التنبؤ به من كود mixGene جيد جدًا ليتم تحليله ودراسته. نأمل أن يحمل تجزئة الكتلة كعامل تحور أيضًا بعض الأهمية الجسدية ، مما يساعد ، على سبيل المثال ، في تحديد الجين الذي يجب تحوره. إذا تمكنا من معرفة ذلك ، فسوف نحصل على الجين الأصلي ، بدون طفرات. هذا مفيد لأنه إذا لم يكن لديك جين مصدر جيد ، فقد لا تكون أفضل طفرة كافية.
كما أننا لم نقيس العلاقة بين الجين 256 بت وسمات القطط (لون العين ، ونوع الذيل ، وما إلى ذلك) ، ولكننا نعتقد أن هذا ممكن تمامًا بمساعدة روبوت عالي الأداء ومصنف بسيط.
وبشكل عام ، نحن نفهم تمامًا نية فريق تطوير CryptoKitties لتحقيق الاستقرار في الطفرة خلال فترة زمنية قصيرة. لكن الوجه الآخر لهذا النهج هو القدرة على إجراء تحليل كما فعلنا.
نود أيضًا أن نشكر مجتمع ethereum الرائع لتطوير أدوات مثل Etherscan و hevm و evmdis و truffle و testrpc و myetherwallet و Solidity. هذا مجتمع رائع للغاية ويسعدنا أن نكون جزءًا منه.
وأخيرًا ، الكود المعدل
https://github.com/modong/GeneScienceCracked/تذكر أن تغير $ CONSTBLOCKHASH $ إلى تجزئة الكتلة المتوقعة.
