شركاء شراكة كالوزا كلاين ، الجزء 2

في مقال سابق ، شرحت لماذا يبدو للمراقبين ساذجين لا يعرفون عن وجود بُعد إضافي أن الجسيم القادر على التحرك في أبعاد إضافية لديه شركاء كالوزا كلاين (KK) - إصدارات أثقل من الجسيم الأصلي. أشرت إلى أنه عندما يتحرك الجسيم الأولي للكتلة m في اتجاه البعد الإضافي ، فإنه يبدو للمراقب الساذج بلا حراك وأثقل مما يجب أن يكون ، كما لو كان جسيمًا من نوع مختلف. تسمى هذه الفئة من الجسيمات التي يفترض أنها جديدة ، على غرار الجسيمات الأصلية ، ولكنها أثقل ، شركاء مراقبة الجودة.

في حالة الشريط ، إذا تحرك جسيم الكتلة m عبر الشريط مع لحظة ع _عبر ، فإن المراقب الذي يعتبر الشريط كخط يفترض أن الجسيم هو شريك KK مع صفر من الزخم والكتلة M ، حيث

$$

$$M ^ 2 = m ^ 2 + (p_ {عبر} / ج) ^ 2> m ^ 2$$

على الرغم من أن هذا صحيح بشكل عام ، فإنه يتبع أنه لكل كتلة M أكبر من m ، يجب أن يكون هناك شريك مراقبة الجودة الخاص بها. لكن الأمر ليس كذلك - عالمنا كمّي (انظر الشكل 1 من المقالة السابقة). الآن نكتشف بالضبط كيف تغير ميكانيكا الكم الصورة بأكملها.

السمة الرئيسية لفيزياء الكم التي نحتاجها هي أنه بالنسبة لـ "جسيم" كمي يتحرك في قياس الحجم المحدود ، لا يُسمح بجميع القيم المحتملة لـ p _عبر . في صياغة أكثر عمومية: تقترح ميكانيكا الكم أن "الجسيم" يتحرك في قياس محدود الحجم يمكن أن يكون له قيم زخم معينة فقط في هذا الاتجاه.

هذه واحدة من أهم وغرابة عواقب ميكانيكا الكم! للوهلة الأولى ، يعد هذا غير بديهي تمامًا ، حيث ما الذي يمكن أن يمنعك من طلب "الجسيم" مع الزخم p تسارعًا طفيفًا بحيث يختلف زخمه قليلاً عن p؟

ما هو الكم؟

ربما لاحظت أني بدأت أقتبس كلمة "جسيم" ، لأننا في السياق الحالي نحتاج إلى تمييز مصطلح "جسيم" ، المستخدم لوصف الإلكترونات والميونات والكواركات والغلوونات وجميع الجسيمات الأولية المعروفة الأخرى ، من مفهوم بديهي الجسيمات التي نرثها من تجربتنا مع الغبار والرمل والملح والحصى. سيكون من الأفضل تسمية مثل هذه "الجسيمات" مثل الإلكترون والفوتون والكوارك ، وما إلى ذلك ، والكميات ، والمزيد من الأشياء الماكرة. هذه الكميات هي اضطرابات في الحقول ؛ فهي تشبه الأمواج أكثر من الجسيمات. أفضل طريقة لفهم الكم هي تخيل الموجات. هذه نقطة لغوية مهمة أخرى: عندما أقول "موجة" ، لا أقصد شيئًا مثل موجة منفصلة في المحيط تنكسر على الشاطئ - أعني سلسلة من الموجات مع العديد من القمم والأحواض.

ومن الأمثلة على هذه الموجات الموجات الكهرومغناطيسية ، والتي تتضمن أيضًا موجات ضوئية ، يمكن تمييزها عن أعيننا. تخيل أننا أخذنا مثل هذه الموجة - على سبيل المثال ، ضوء الليزر - وقمنا بتعتيم الضوء أكثر وأكثر. كيف يمكن أن تكون مكتومة؟ اتضح أنه في عالمنا الكمي هناك وميض ضوء خافت ممكن نسميه كمًا من الضوء أو الفوتون. الفوتون هو موجة من الضوء ذات ارتفاع وكثافة الموجة هي الأصغر على الإطلاق. نحن مدينون بكل هذه المفاهيم والأسماء لأينشتاين ، الذي - على الرغم من استياءه المعروف من العواقب المفاهيمية لميكانيكا الكم - كان أحد مؤسسي هذه النظرية.

لا يوجد شيء بديهي - من وجهة نظري - أن الموجات الضوئية تتكون من كميات ، لأن هذا لا يتجلى في أي من العمليات التي نلاحظها مباشرة. لكن أجسادنا ، بفضل العمليات التي لا ندركها ، تستخدم هذه الحقيقة باستمرار. يبدو ضوء المصباح متواصلًا لدماغنا ، لكن أعيننا تمتص الفوتونات في كل مرة. علاوة على ذلك ، رأيت بأم عيني التأكيد على أن الضوء يتكون من الكمي - أعرف عن هذا ليس فقط من الكتب.

نحن الفيزيائيون نسمي غالبًا هذه الكميات الضوئية "جزيئات الضوء" ، لأنها تتصرف من نواح كثيرة مثل الجسيمات. أي فوتون يتحرك في خط مستقيم بنفسه لديه طاقة وزخم معين ؛ جميع الفوتونات لها نفس قيمة الكتلة (على وجه التحديد ، صفر) ؛ لا يمكن تقسيم الفوتون إلى أجزاء أصغر ؛ لا يمكن انبعاث الفوتون أو امتصاصه بالكامل. تتوافق هذه الخصائص تقريبًا مع ما يمكن أن يتوقعه حدسنا من الجسيمات مثل حبيبات الرمل والكرات الزجاجية وجزيئات الغبار وما إلى ذلك.

لكن كلمة "كمومي" لأسباب عديدة أفضل من كلمة "جسيم" ، لأن بعض خواص الكوانتا تشبه خصائص الجسيمات ، وبعضها لخصائص الموجات. مثال معروف لسلوك الموجة هو طريقة كمية لتمرير من خلال بابين في وقت واحد والتفاعل (بنفس المعنى الذي تتفاعل فيه الموجات مع بعضها البعض وتتدحرج مع أحواض تدمر بعضها البعض) مع نفسها. ثم سنرى مثالاً آخر.

يجب أن نتذكر أن ما يتم فعله للفوتون يتم أيضًا لجميع "الجسيمات" المعروفة. في الواقع ، كل واحد منهم هو نوع من الكم - موجات أدنى ارتفاع ممكن في المجال المقابل. الإلكترون هو كم مجال إلكتروني. الكوارك هو كمية من حقل الكوارك. الجسيمات Z هي كمية المجال Z ، وما إلى ذلك.

Quantums - شركاء مراقبة الجودة

لقد حان الوقت لمعرفة ما وعدت بشرحه لكم: لماذا تعني الطبيعة الموجية للكميات أن كتل جسيمات شركاء KK تأخذ قيمًا محددة ، وليس كل القيم الممكنة ، كتل كبيرة م من "الجسيم" الأصلي. الفيزيائي الشهير لويس دي بروجلي ، بعد آثار أفكار آينشتاين الأولى ، حدد بوضوح لأول مرة أن العلاقة بين الموجات والجسيمات والكميات تعني ضمنيًا أن هناك علاقة بين الكم:
• دافعه (خاصية تشبه خصائص الجسيمات) ،
• وطول الموجة (خاصية تشبه خصائص الموجات) [ومرة أخرى ، هنا بعبارة "الموجة" نعني تسلسل موجات ، ويشير الطول الموجي إلى المسافة بين قمم الموجات في التسلسل].

ويتم التعبير عن هذا الاعتماد ببساطة: الزخم = h / الطول الموجي

ح هو ثابت بلانك الشهير ، وهو نفس ثابت الطبيعة الأساسي مثل سرعة الضوء. قدم بلانك هذا الثابت في عام 1900 ، محاولاً كشف ظاهرة فيزيائية غامضة. كانت هذه الخطوة الأولى نحو الطبيعة الكمية للعالم. في كل مرة تحاول فيها وصف ظاهرة تلعب فيها ميكانيكا الكم دورًا مهمًا ، يظهر الثابت h. في العديد من الصيغ ، يمكنك رؤية القيمة ℏ ، وهذا يتم قسمة h على 2π ، نظرًا لأن هذه القيمة غالبًا ما تكون أكثر ملاءمة لتبسيط الصيغ.


التين. 1: ضع في اعتبارك كمية تتحرك على طول شريط وعلى طول أنبوب

في بعض الحالات ، اتضح أن تفسير ما يحدث للكم يتحرك على طول الأنبوب أسهل قليلاً من تفسير ما يتحرك على طول الشريط الذي استخدمناه في الأمثلة السابقة. تقريبا كل ما يعمل للأنبوب سيكون صحيحًا للشريط. لذلك ، سأستخدمهما معًا.

الشريك الأخف لمراقبة الجودة

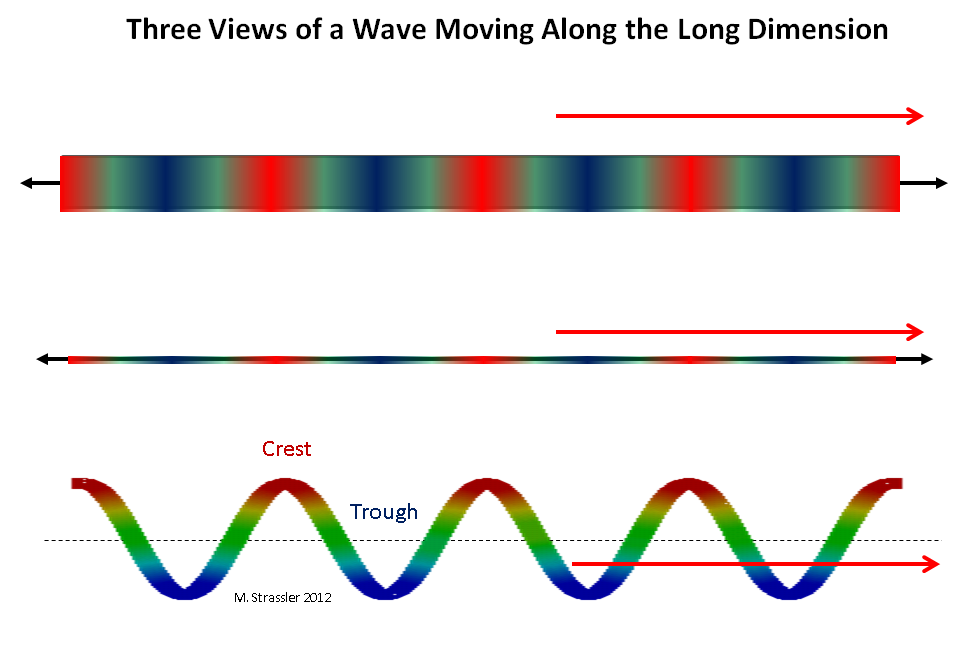التين. 2: ثلاث وجهات نظر لموجة تتحرك على بعد طويل

تخيل كمًا يسافر على طول شريط عرض W ، أو على طول أنبوب دائرة S. أولاً ، تخيل كمًا يتحرك على طول بُعد طويل (يعني طويل لانهائي ، أو طالما أنه يمكن أن يكون لانهائي ، بقدر ما يمكننا الحكم عليه). يمكن أن تتحرك الموجة الممتدة على طول شريط أو أنبوب على طول بُعد طويل في أي اتجاه ولها أي طول موجي (المسافة بين حدين متجاورين). انظر الشكل. 2. يمكن أن يكون لهذا الكم أي زخم على طول شريط أو أنبوب ، وفقًا لـ de Broglie: يمكن أن يكون الزخم صفرًا ، صغيرًا جدًا ، صغيرًا ، كبيرًا ، في أي اتجاه ، إلخ. من حيث المبدأ ، يمكن جعل الاندفاع أكثر قليلاً (أو أقل قليلاً) عن طريق دفع الكم في اتجاه حركته (أو في الاتجاه المعاكس).


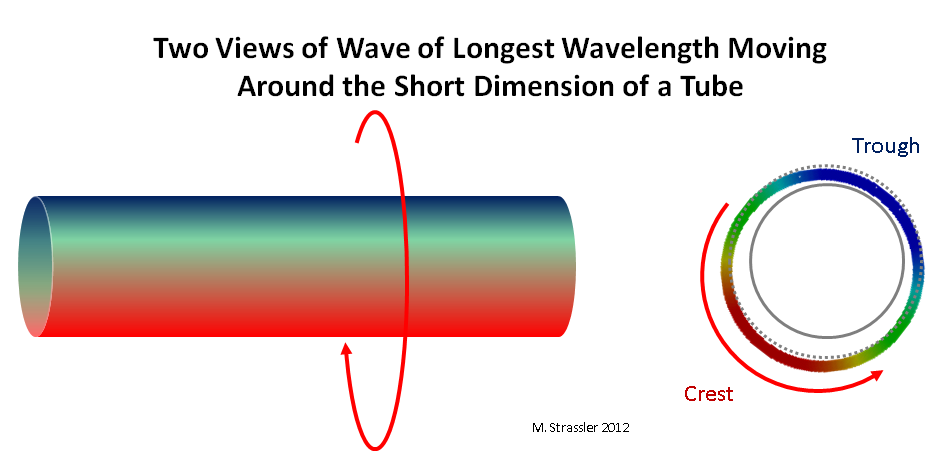التين. 3: نظرتان لموجة تتحرك على بعد قصير للأنبوب

ضع في اعتبارك الآن كمًا (أي "جسيم") يتحرك عبر شريط أو أنبوب. أولاً ، من الواضح أنها لن تكون قادرة على الحصول على طول موجي أكبر من المسافة المستعرضة للشريط أو محيط الأنبوب! يسهل رؤية هذا على الأنبوب: سلسلة واحدة على الأقل (حمراء) واكتئاب واحد (أزرق) يتناسبان مع الأنبوب ، كما هو موضح في الشكل. 3. إذا كان الطول الموجي أكبر من S ، فإن الموجة لن تتصل بنفسها ، كما هو موضح في الشكل. 4. أطول طول موجي هو S بالضبط. ويجب أن يكون التجويف الوحيد للموجة موجودًا تمامًا على جانب الأنبوب المقابل للقمة الوحيدة.


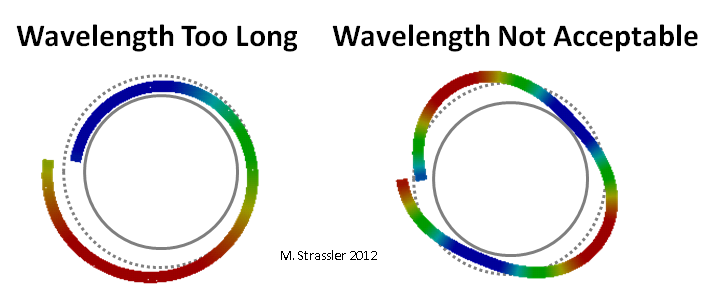التين. 4: أطوال موجية غير ملائمة

قمة وقاع الموجة في الشكل. 3 تتحرك حول الأنبوب ، تشبه (الشكل 5) جسيم عادي غير كمومي (هنا أقصد حقًا شيء مثل حبة الرمل ، وليس كمًا أو "جسيم") يتدحرج على طول الأنبوب ، ولكن مع فرق واحد مهم: إذا لم يكن للجسيم الحدسي العادي أي مشاكل يمكن أن يتحرك بشكل أسرع أو أبطأ قليلاً ، والذي بسببه سيزيد زخمه أو ينخفض ​​قليلاً ، لا يمكن أن يكون للكمية المقابلة للموجة زخم أكبر أو أصغر قليلاً ، لأن هذا سيتوافق مع طول موجة غير مقبول (الشكل 4).


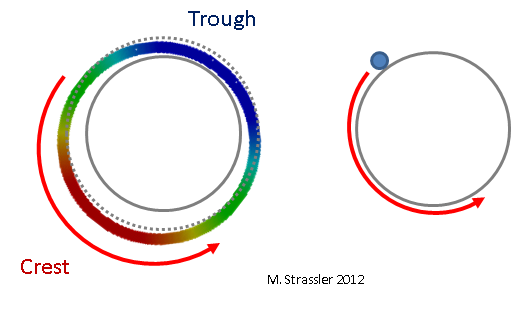التين. 5: موجة تشبه الجسيمات

على الشريط ، يكون الأمر أكثر صعوبة ، ولكن كما هو موضح في الشكل. 6 ، مرة أخرى ، يمكن أن يكون هناك شعار واحد فقط على أحد الجدران وآخر على الآخر ، ويتغير هذا الوضع بمرور الوقت: لا يتحرك الشعار ، ولكنه يتقلص في الحجم ويتحول إلى تجويف ، ويتحول التجويف إلى قمة. لاحظ أنه على عكس الشكل. 3 ، حيث تحتفظ القمة والخندق بحجمها ولكنها تتحرك على طول الأنبوب ، لا تتحرك قمة هذه الموجة ، بل تنقبض. لذلك ، يطلق عليها "الموجة الواقفة". لمثال مماثل (ولكن ليس متطابقًا) ، تخيل سلسلة من الغيتار أو الكمان. بشكل بديهي ، تتوافق هذه الموجة الدائمة مع جسيم عادي غير كمي يتحرك للأمام والخلف عبر شريط. (أقل بديهية ، ولكن بشكل أدق ، تتوافق مع جسيم عادي يتحرك في كلا الاتجاهين في نفس الوقت. لكن هذه الحقيقة الكمية الغريبة والباردة غير مهمة الآن.) يظهر هذا في الشكل. 7.


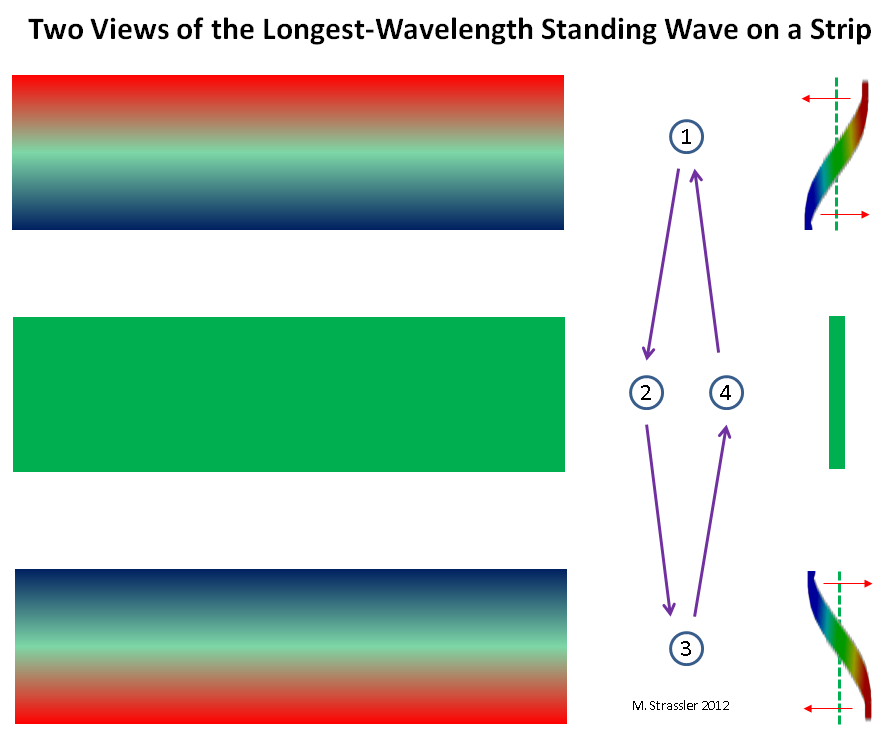التين. 6: منظران للموجة الدائمة بأطول طول موجي

في كلتا الحالتين ، هناك أكبر طول ممكن للموجة (S للأنبوب ، 2W للشريط). وهذا يعني أن هناك أصغر دفعة ممكنة (h / S و h / 2 W للأنبوب والشريط). وأخيرًا ، هذا يعني أن هناك أسهل جسيم KK ممكن! مع الكتلة M ، أين

$$

$$M ^ 2 = m ^ 2 + (p_ {عبر} / c) ^ 2 = m ^ 2 + (h / c S) ^ 2 \ quad (pipe) \\ M ^ 2 = m ^ 2 + (p_ { عبر} / c) ^ 2 = m ^ 2 + (h / 2 c W) ^ 2 \ quad (strip)$$

لاحظ أنه بالنسبة للجسيمات عديمة الكتلة ، م = 0 ، يتم تقليل هذه الصيغ إلى:

$$

$$M = h / c S \ quad (pipe) \\ M = h / 2 c W \ quad (strip)$$

وهذه الصيغ الأخيرة صحيحة تقريبًا إذا كانت S و W صغيرة جدًا ، كما هو الحال غالبًا في الاستدلال المعقول.


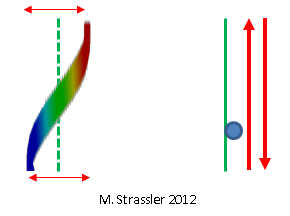التين. 7: كم الموجة الدائمة يشبه الجسيم يتحرك ذهابًا وإيابًا

وهكذا تعلمنا أنه نظرًا لحقيقة أن "الجسيمات" هي في الواقع كمية ، مع خصائص تشبه خصائص الموجات:

• في شريك KK الأخف ، تكون الكتلة M أكبر بكثير من m ،
• بما أن الصيغ لـ M تتضمن 1 / W و 1 / S ، كلما كان البعد الإضافي أصغر ، كلما كان شريك KK الأخف وزنًا أصعب.
• في الواقع ، عندما تصبح S و W صغيرة جدًا بحيث يتجاوز M بشكل كبير m (أو إذا كان m مبدئيًا على الإطلاق) ، فإن M تتناسب تقريبًا مع 1 / S أو 1 / W.

عظيم. هذه هي النقطة الرئيسية ، لذا يرجى التأكد من فهمها قبل المتابعة. هناك شيء آخر لا يزال يتعين شرحه:

• لماذا يوجد العديد من شركاء KK بكتل مختلفة M ، M ، M ، إلخ. (حيث ، بحكم التعريف ، M <M '<M "، إلخ.)
• لماذا يتم فصل هذه الكتل عن بعضها البعض.
• لماذا تنمو الكتل مع تناقص البعد الإضافي.
• لماذا يمتلك شركاء KK من أنواع مختلفة من الجسيمات القادرة على التحرك في نفس البعد الإضافي كتل متشابهة ، خاصة لشركاء KK الأثقل.
• لماذا ستقدم لنا جماهير شركاء مراقبة الجودة معلومات مباشرة حول شكل وحجم وعدد القياسات الإضافية.

من الإجابات أعلاه يمكن استنتاجها بسهولة إلى حد ما.

أبعد من شريك أخف QC

التين. 8: الموجة الأقرب إلى الطول الموجي الأطول ، تتحرك على طول البعد القصير للأنبوب

لماذا يوجد العديد من شركاء KK؟ فقط لأن الموجات الكمومية على شريط أو أنبوب يمكن أن يكون لها العديد من الأطوال الموجية المختلفة. في الشكل. 8 و 9 و 10 ، يمكن للمرء أن يرى موجات يبلغ طولها 1/2 أو 1/3 من الحد الأقصى ، المقابلة (وفقًا لأينشتاين ودي بروجلي) مع كم من النبضات المزدوجة والثلاثية فيما يتعلق بالحد الأدنى.


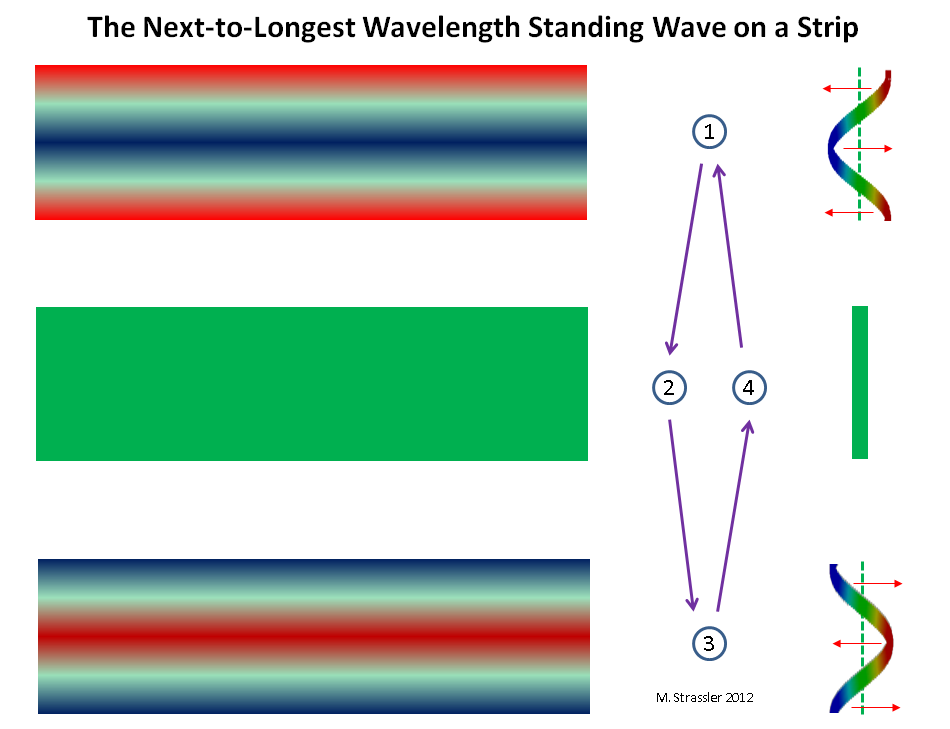التين. 9 موجة واقفة قريبة من الطول الموجي الأطول على الشريط

تلخيص ، يمكننا القول أن أي طول موجي مقبول ، والذي يحتوي على n حواف و n أحواض ، حيث n هو أي عدد صحيح موجب (1 ، 2 ، 3 ، 4 ، ..) ، بحيث يكون الطول الموجي يساوي S مقسومًا على n (أو 2W مقسومة على n) والموجة تناسب بشكل واضح داخل دائرة من دائرة S أو داخل خط بطول W. أي طول موجي آخر غير مناسب (انظر الشكل 4). وفقًا لذلك ، مع الأخذ في الاعتبار علاقة de Broglie ، الزخم = h / wave_length ، يُسمح بأي دفعة للشكل nh / S (أو nh / 2 W) ، ولكل قيمة n سيكون لدينا شريك كتلة KK:

$$

$$M ^ 2 = m ^ 2 + (p_ {عبر} / c) ^ 2 = m ^ 2 + (nh / c S) ^ 2 \ quad (pipe) \\ M ^ 2 = m ^ 2 + (p_ { عبر} / c) ^ 2 = m ^ 2 + (nh / 2 c W) ^ 2 \ quad (strip)$$

هذا يجيب على جميع الأسئلة المطروحة تقريبًا ، على الأقل للحالات ذات الأنبوب والشريط:

• هناك العديد من شركاء مراقبة الجودة (واحد لكل n> 0) ،
• يتم فصل كتلها جيدًا عن بعضها البعض (حيث عندما يتغير n بمقدار 1 ، يتغير M كثيرًا) ،
• تنمو كتلها مع انخفاض في الأبعاد الإضافية (نظرًا لأن المصطلحات الأخيرة في الصيغ تصبح أكبر عندما تصبح W و S أصغر) ،
• شركاء KK الثقيلون من الجسيمات المختلفة ذات الكتل المختلفة m لديهم كتل متشابهة M ، لأنه بالنسبة إلى n بما فيه الكفاية ، تكون المصطلحات الثانية في الصيغ كبيرة مقارنة بـ m ² ، مما يعطي كتلة شريك KK تساوي تقريبًا M = nh / c S للأنبوب و nh / 2 ج وات للشريط ، وهي تكاد تكون مستقلة عن م.

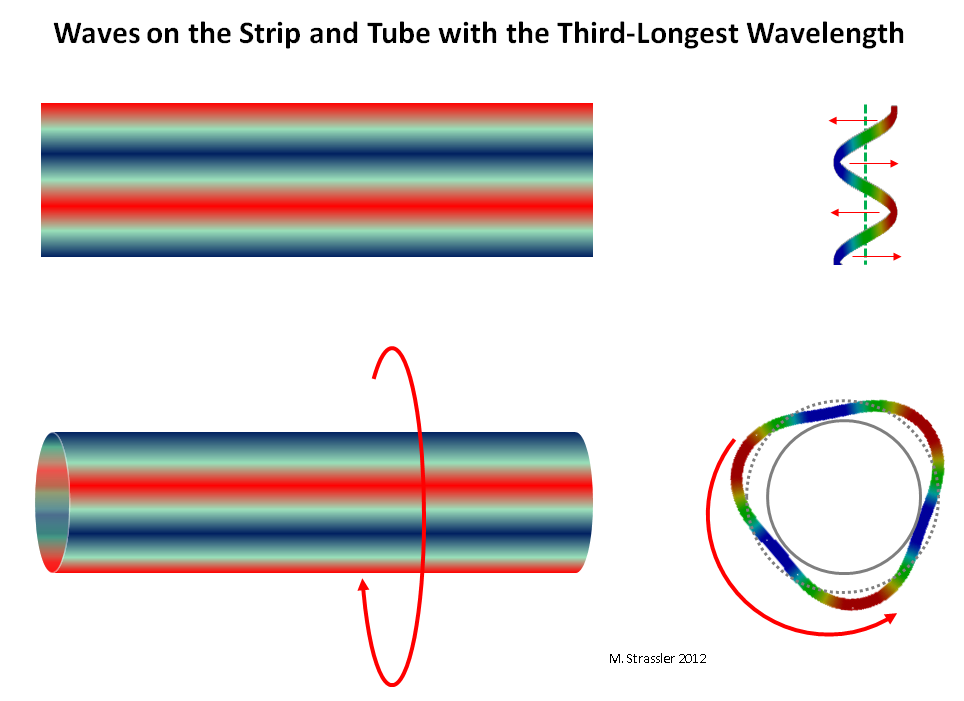التين. 10: موجات على شريط وأنبوب بطول موجة 1/3 كحد أقصى

يبقى السؤال الأخير: لماذا تحدد كمية الأبعاد الإضافية وحجمها وشكلها كتل شركاء KK - وبالتالي ، لماذا يسمح لك القياس الشامل للعديد من شركاء KK بتحديد خصائص القياسات الإضافية ، تمامًا مثل الاستماع إلى صوت آلة موسيقية تسمح لك بتحديد شكلها بشكل أساسي والحجم والمواد التي صنعت منها؟

خذ مثال مبسط للغاية. سننظر في بعدين إضافيين ، مرة أخرى باستخدام قناة السفن الكلاسيكية لدينا ، بما في ذلك (كما فعلنا في نهاية مقال حديث مع أمثلة على قياسات إضافية) وحقيقة أن القناة لها عمق ، حتى نتخيل الموجات داخلها (يمكنك الموجات من هذا النوع نسمع في غرفة كبيرة ، أو تحت الماء في أي قناة). سيكون جزء القناة (إذا قطعناه في أي نقطة من الخط على طول البعد الطويل) مجرد مستطيل بعرض W وعمق D. تمامًا مثل أي جسيم غير كمومي ، حتى إذا كان ثابتًا من وجهة نظر البعد الطويل ، يمكن أن يتحرك على طول واحد أو اثنين إضافيين القياسات (وبالتالي ، يكون لها نبض إما في العرض أو في العمق) ، وسيكون للموجة طول موجة في كلا البعدين الإضافيين. مثل هذا التقسيم البسيط للموجة إلى ما تفعله عن طريق قياس العرض وما تفعله بقياس العمق مرتبط بشكل خاص بمستطيل القناة ، وعادة لن يعمل في أمثلة أخرى. على سبيل المثال ، كما هو موضح في الشكل. 11 ، في الأعلى ، ستحتوي إحدى الموجات المسموح بها على ثلاث أحواض لقياس العرض وواحدة لقياس العمق.


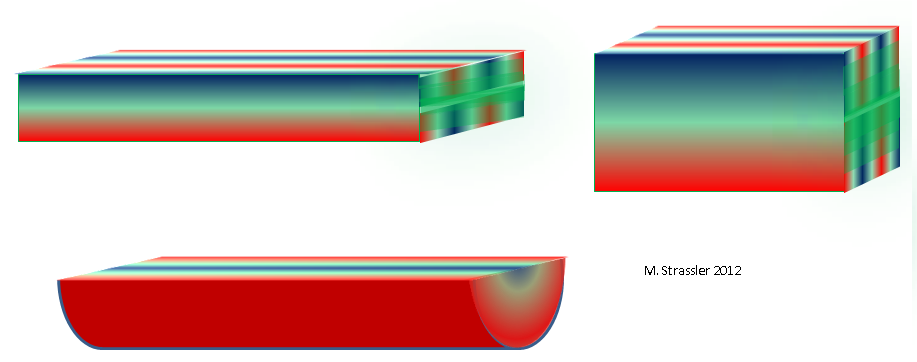التين. 11

يمكننا تحديد عدد المنخفضات والتلال بقياس العرض مع العدد الصحيح n ₁ ، وبقياس العمق - n ₂ ، ولكل من n ₁ و n ₂ (يمكن أن تكون واحدة أو كلتا هاتين القيمتين أكبر من الصفر) ، نحصل على شريك KK. بالنسبة للكميات عديمة الكتلة (م = 0) أو الكميات بلا كتلة تقريبًا ، سيكون لدى شركاء KK كتلة

$$

$$M ^ 2 = m ^ 2 + (p_ {width} / c) ^ 2 + (p_ {عمق} / ج) ^ 2 = m ^ 2 + (n_1 h / 2 c W) ^ 2 + (n_2 h / 2 ج د) ^ 2$$

يمكن ملاحظة أن التوزيع الجماعي يختلف عن الحالة مع بعد إضافي واحد ، ويمكن أن يخبرنا كل من W و D.

إذا كان المقطع العرضي للقناة مختلف الشكل ، على سبيل المثال ، مثلث أو نصف قرص ، كما هو موضح في الشكل. 11 ، أدناه ، نحصل على توزيع جماعي آخر يعكس الشكل الدقيق لمثلث أو نصف قرص. ويمكننا بالفعل تجاهل قنوات السفن العملية وتمثيل الفضاء ثلاثي الأبعاد ، الذي يتوافق المقطع العرضي مع أي شكل آخر ثنائي الأبعاد محدود ، يظهر أحدها في الشكل. 1 في مقال عن عوالم ذات مكانيين: قرص ممتلئ ، أو حتى كرة أو حيد. سيعطينا كل من هذه الأشكال نوعًا خاصًا به من التوزيع الجماعي لشركاء مراقبة الجودة. وإذا كان هناك ثلاثة أو أربعة أو خمسة أبعاد إضافية ... ربما أكثر من أنواع التوزيعات.

أمثلة على بعض التوزيعات للجسيمات عديمة الكتلة بأحجام من القياسات الإضافية المختارة بحيث تكون كتل شركاء KK الأوائل هي نفسها لكل حالة في الشكل. 12. من الواضح أنه من أجل تحديد شكل وحجم القياسات الإضافية ، من الضروري قياس كتل عدد كبير بما فيه الكفاية من شركاء KK (وحتى على الأقل التأكد من أن أي من الجسيمات الثقيلة المكتشفة حديثًا هي بشكل عام شركاء KK) ، من أجل فهم طبيعة أي قياسات إضافية القياسات ، سيمر الوقت.


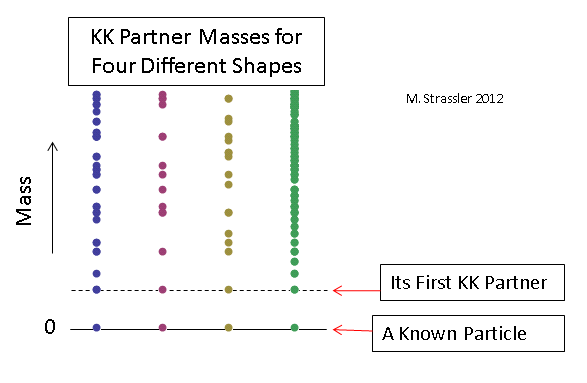التين. 12

ولكن هل يمكن أن تكون جسيمات المادة الثقيلة المعروفة شركاء KK لجسيمات أخف؟

ثم يطرح السؤال الإضافي الواضح.نحن نعلم أنه من بين الجسيمات الأولية المعروفة يوجد إلكترون ، وكذلك إصداراته الأثقل: muon و tau. هناك كوارك علوي ، ونسخته الأثقل ساحرة وصحيحة. هناك كوارك أقل ، ونسخته الأثقل ، غريبة وساحرة. هي إصدارات الجسيمات الثقيلة شركاء مراقبة الجودة في الرئتين؟

للوهلة الأولى ، هذا افتراض مغري ، لكن الإجابة عليه ستكون لا. آسف.هذا ليس سؤال غبي لديها فقط جواب سلبي ذكي.

ميون وتاو ، مسحوران وصحيحان ، غريبان وساحران - كلهم ​​يحصلون على كتلهم بفضل حقل هيجز ، وليس بفضل الدافع من أبعاد إضافية. هذا يتبع بوضوح من التجارب التفصيلية. يمكن العثور على نصائح في المقالة حول ما سيحدث إذا كان حقل هيجز صفرًا . لاحظ أنه إذا كان حقل هيجز صفرًا في المتوسط ​​، فلن يكون للإلكترون والميون والتاو كتلة (وسيتكسر كل منها إلى نوعين من الجسيمات). هذا لا يتوافق مع النظرية القائلة بأن الميون وتاو هم شركاء KK للإلكترون.

هناك العديد من الأسباب الأخرى. ربما يكون أخطرها أنه بسبب وجود شحنة على الإلكترون وبسبب حقيقة أنه محاط بمجال كهربائي ، يجب أن يتحرك الفوتون في أي بعد يتحرك فيه الإلكترون (على الرغم من أن العكس غير صحيح). لذلك إذا كان الإلكترون لديه شركاء KK ، فيجب أن يكون الفوتون لديهم أيضًا. ولكنه يستنتج من صيغنا (وما شابهها أكثر عمومية) أنه نظرًا لعدم وجود كتلة للفوتون ، وكتلة الإلكترون (0.0005 GeV / c ² ) صغيرة مقارنة بكتلة الميون (حوالي 0.1 GeV / c ²) ، إذا كان الميون شريك KK ، فيجب أن يكون للفوتون شريك KK بكتلة مماثلة. لكن هذا الجسيم ، إن وجد ، كان سيتم اكتشافه قبل سنوات عديدة. في الواقع ، لم يلاحظ شركاء KK للفوتونات في التجارب التي تمت فيها دراسة كتل أكبر بكثير من كتلة جزيئات Z - هذه مئات عديدة من GeV / s ² . لا يمكن أن يكون الجسيم Z نفسه شريكًا لمراقبة الجودة للفوتون ؛ لا تبدو مثله بما فيه الكفاية. وهذا يعني أن أي شريك KK للإلكترون يجب أن يكون ثقيلًا على الأقل.

إلى أين أذهب بعد ذلك؟ للتجارب

انتقلنا من النظرية (إمكانية القياسات الإضافية والرياضيات والهندسة ذات الصلة) إلى التوقعات (شركاء مراقبة الجودة). الخطوة التالية: ماذا نعرف عن القياسات الإضافية من التجارب؟ لم نر بعد شركاء KK في التجارب ، ولكن قد نسأل ، ماذا يمكننا أن نتعلم من غيابهم؟ كثيرًا جدًا ، كما سأشرح لاحقًا ، جنبًا إلى جنب مع وصف لكيفية استمرار محاولات العثور على علامات للقياسات الإضافية في Large Hadron Collider وأماكن أخرى.