هل كوننا لانهائي؟
إنتباه! في هذه المقالة ، سيتم التعبير عن نظرية فقط ، بدون دليل علمي.
يوم جيد Giktayms! لقد دفعتني لكتابة هذا المقال بواسطة فيديو على YouTube حول مفارقات عددية غير عادية. وهي مفارقات
زينو ولماذا يستحيل القسمة على صفر ، والتي سيتم مناقشتها اليوم.
يمكن تفسير مفارقة زينو بسهولة كبيرة على أساس
أخيل والسلحفاة. أولئك الذين ليسوا على دراية بهذا التناقض ، هنا فيديو مرئي لمؤلف آخر:
أوصي بأن تقرأ قبل قراءة المزيد. (مفارقة أخيل والسلاحف)
(مفارقة أخيل والسلاحف)إذا كنت لا ترغب في مشاهدة الفيديو ، فسأخبرك بإيجاز: تخيل أن أخيل يركض خلف سلحفاة تفوقه. المسافة بينهما تتناقص باستمرار ، حيث تعمل أخيل بشكل أسرع من السلاحف. ونتيجة لذلك ، عندما تقترب أخيل من مسافة متر واحد ، بعد فترة ستكون مساوية لـ
0.1 متر ، ثم
0.01 ، وهكذا إلى ما لا نهاية. هذا يعني أن أخيل لن يلحق بالسلحفاة أبدًا ، ولكن في الواقع كل شيء خاطئ تمامًا.
في الواقع ، لا توجد مشكلة ، فنحن نأخذ أخيل والسلحفاة ، ونضعها على جهاز المشي ونرجوك ، يتخطى أخيل بهدوء السلحفاة. في هذا بالضبط ، يكمن الدليل المحتمل على أن الكون ليس لانهائي.
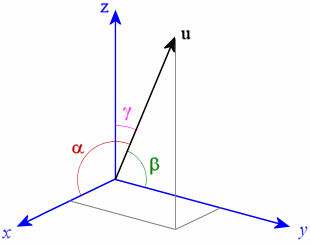 (ناقل في مساحة ثلاثية الأبعاد)
(ناقل في مساحة ثلاثية الأبعاد)دعونا نحاول شرح هذا على مبدأ ألعاب الكمبيوتر. بشكل نموذجي ، يتم كتابة موضع الكائن كمتجه يتكون من محاور x و y و z. ويتم تخزين كل قيمة في
تعويم نوع البيانات
(قيمة النقطة العائمة) . على سبيل المثال ، يستخدم
Unity3D تعويم 32 بت للإشارة إلى موقعه في الفضاء. القيمة الدنيا منها:
1،175494351 E - 38. ، والتي تعطي حركة سلسة على أي مقياس تقريبًا. هنا الكلمة المهمة هي
"تقريبًا" ، أي إذا قللنا النموذج تقريبًا تقريبًا ، فسوف نرى كيف يتحرك في القفزات. القفز من
0 ، ... 1 إلى
0 ، ... 2 إلى
0 ، ... 3 ، إلخ. هذا يعني أنه في المحاكاة ، في أي سيناريو ، سيتغلب أخيل على السلحفاة. ولكن كما يقولون لا يوجد شر بدون خير. إذا كان لدينا الحد الأدنى من القيمة العائمة ، فهناك حد أقصى ، إذا جاز التعبير ، من مساحة
ثلاثية الأبعاد . تجاوز ذلك لن يسمح لنا
(دعونا نطلق عليه) قوانين فيزياء العالم الافتراضي. في الواقع ، لا يمكننا ببساطة إعطاء أكثر من القيمة القصوى للمتغير.
إذا عدنا إلى مفارقة زينو ، فلن يلحق أخيل بالسلحفاة أبدًا فحسب ، بل لن يصل أبدًا إلى حدود عالمه الخيالي ، لأنه سيكون بلا حدود. من -∞ إلى + ∞ ، الغريب ، نحصل على نفس الوظيفة
f (x) = 1 / x . والشيء الأكثر تسلية هو أن قيمة
x / 0 لا تقع في هذه الوظيفة ، لأن الوظيفة لن تصل أبدًا إلى الصفر ، مثل سلحفاة الأخيل.
(في الواقع ، لا يمكن تقسيم هذا على صفر)يكفي النظرية ، دعنا نتدرب. خذ العالم الحقيقي ، فكلنا يتكون من ذرات ، وتتكون الذرات من بروتونات نيوترونية وإلكترونات ، والتي بدورها تتكون من كواركات
(جسيمات أولية) . في كل من المحاكاة والعالم الحقيقي ، لا يحتاج أخيل إلى تجاوز سلحفاة. كل هذا يؤدي إلى حقيقة أنه ، في كل من المحاكاة وفي الواقع ، يجب أن تقفز الجسيمات الأولية أيضًا بالأرقام
0 ، ... 1 0 ، ... 2 0 ، ... 3 كما يحدث في اللعبة ، لأن أخيل يمكن أن تتجاوز سلحفاة هنا وهناك. يخبرنا هذا أن مفارقة Zeno تعمل فقط على الورق ، أو في نظام الإحداثيات الخاص بها ، والتي تتراوح قيمتها من -∞ إلى + ∞. في الواقع ، عند القفز على أصغر القيم ، فإن الجزيئات الأولية من أخيل تتفوق على السلحفاة في وقت ما ، وتصبح إحداثياتها متساوية ، وبعد ذلك يمتد أخيل إلى الأمام.
لذلك تعلمنا ما هو نظام التنسيق الذي تستخدمه مساحتنا ، فلنعد إلى الموضوع الرئيسي. إذا كان لدينا حد أدنى للقيمة ، فسيكون هناك حد أقصى -
حافة الكون . هناك من سيقول لماذا إذن ، من ناحية ، يمكن أن يكون لانهائي ، ومن ناحية أخرى ، محدود. لكن المشكلة هي أن الإحداثيات أو الموضع ليست سوى عنصر من نظام كبير يسمى الفضاء ، ويمكن أن يكون إما لانهائي تمامًا أو محدود تمامًا. أيضا ، كل هذا يطرح السؤال ، وبالصدفة لسنا في محاكاة كمبيوتر ، أليس كذلك؟ لكن هذا موضوع لمقال آخر.
الملخص
لذلك وصلنا اليوم إلى استنتاج مفاده أن الكون
ليس لانهائي ، في هذا المنشور فقط تم التعبير عن النظرية كيف لا أحد يعرف الكون هناك حقًا ، ولا يمكنه إثباته. ولكن ربما مع هذه المقالة ، دفعت شخصًا ما لاكتشاف اكتشافات جديدة.
المصدر