تصف معادلات نافير-ستوكس الظواهر اليومية البسيطة ، مثل المياه المتدفقة من خرطوم الحديقة - ومع ذلك ، فهي تستند إلى مشكلة تم تقدير حلها بمليون دولار

في الفيزياء ، هناك معادلات تصف كل شيء من التمدد الزماني إلى رحلة الفوتون. ومع ذلك ، تعتبر مجموعة واحدة فقط من المعادلات معقدة للغاية من الناحية الرياضية بحيث تم اختيارها كواحدة من
مشكلات الألفية السبع ، والتي يقدم
معهد كلاي للرياضيات جائزة قدرها مليون دولار: هذه هي
معادلات نافير-ستوكس التي تصف تدفق السوائل.
لقد
كتبت مؤخرًا عن كيفية الحصول على نتيجة جديدة مهمة لهذه المعادلات. ويشير هذا العمل إلى أن التقدم نحو جائزة الألفية سيكون أكثر صعوبة مما كان متوقعا. لماذا تصف هذه المعادلات ظواهر مألوفة مثل تدفق المياه من خلال خرطوم رياضي أكثر صعوبة في الفهم من معادلات حقل آينشتاين ، التي تشمل أجسامًا مذهلة مثل الثقوب السوداء؟
الجواب ، كما أفهمه ، يكمن في الاضطراب. لقد عانينا جميعًا من هذه الظاهرة ، أثناء الطيران في هواء غير متجانس على ارتفاع 10000 متر ، أو عند ملاحظة قمع من الماء يخرج من المصرف في الحمام. ومع ذلك ، لا تتبع المعرفة من الوعي: الاضطراب هو أحد أقل المجالات فهمًا في العالم المادي.
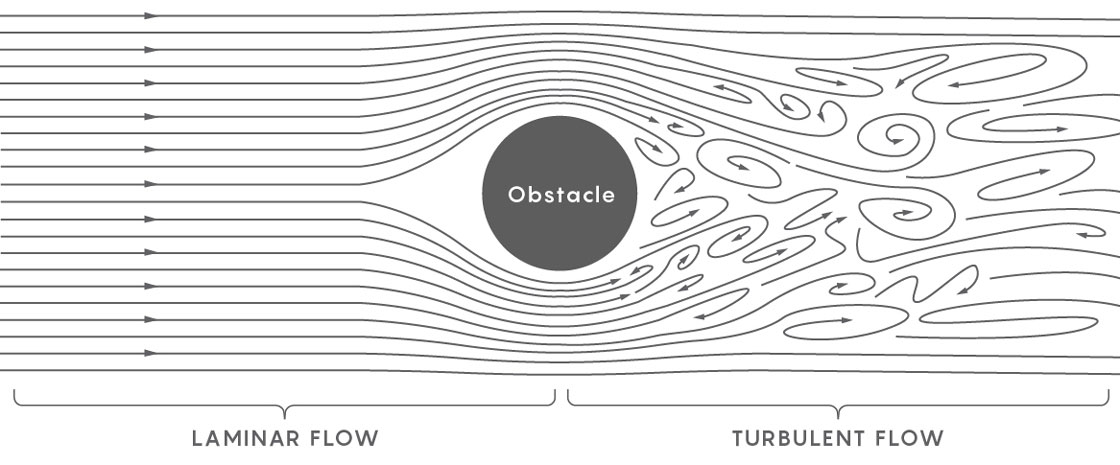
مثال على التدفق دون الاضطراب هو نهر هادئ. يتحرك كل جزء منه في نفس الاتجاه وبنفس السرعة. يظهر السائل المضطرب عندما ينكسر مجرى النهر بحيث تبدأ أجزاء مختلفة من المجرى في التحرك في اتجاهات مختلفة بسرعات مختلفة. يصف الفيزيائيون تشكيل الاضطراب في البداية على أنه شكل قمع في تدفق سلس ، ثم على شكل قمع صغيرة في القمع الأول ، وحتى مسارات أصغر في هذه القمع - بحر من القمع يدخل إلى السائل ، بحيث يتكسر السائل إلى أجزاء منفصلة ، كل منها يتفاعل مع بعضها البعض ويتحرك في اتجاهه الخاص.
يريد الباحثون أن يفهموا بالضبط كيف ينقسم التدفق السلس إلى اضطراب مضطرب ، ونمذجة الشكل المستقبلي للسائل بعد أن يكون للاضطراب أثره. لكن هدف الألفية تم صياغته بشكل أكثر تواضعا: ما عليك سوى إثبات أن الحلول موجودة دائما. أي ، السؤال هو ، هل يمكن للمعادلات أن تصف أي سائل ، مع أي شروط أولية ، وإلى مستقبل بعيد إلى ما لا نهاية؟
يقول تشارلي فيفرمان ، عالم الرياضيات في جامعة برينستون: "الخطوة الأولى هي ببساطة محاولة إثبات أن المعادلات لها بعض الحلول". "هذا لا يعطي فهمًا حقيقيًا لسلوك السوائل ، ولكن إذا لم يكن لديك هذا أيضًا ، فأنت لا تعرف أي شيء على الإطلاق."
إذن كيف يمكن للمرء أن يثبت وجود الحلول؟ عليك أن تبدأ بفهم سبب عدم وجودهم. معادلات نافيير-ستوكس تعني حساب التغيرات في كميات مثل السرعة والضغط. يشعر علماء الرياضيات بالقلق من السيناريو التالي: أنت تهرب من هذه المعادلات ، وبعد مرور بعض الوقت المحدود يقولون لك أن جزيء مائع يتحرك بسرعة لا نهائية. وهذه هي المشكلة - لحساب التغيير في القيمة اللانهائية ليس أسهل من القسمة على صفر. يصف علماء الرياضيات مثل هذه المواقف بأنها "انفجار" ، وفي حالة حدوث انفجار ، تتوقف المعادلات عن العمل ولا يتم العثور على حلول.
 تصف معادلات نافير-ستوكس تدفق السائل غير القابل للضغط.
تصف معادلات نافير-ستوكس تدفق السائل غير القابل للضغط.
بشكل عام ، منتج الكتلة (الجزء الأزرق) والتسارع (البنفسجي) يساوي القوى المؤثرة على السائل (البرتقالي):- ρ هي كثافة السائل ؛
- dV / dt - التغيير في السرعة بمرور الوقت ؛
- V ∇V - سرعة واتجاه الحركة ؛
- ∇P - تغير الضغط الداخلي ؛
- ρ ز - تأثير القوى الخارجية (مثل الجاذبية) ؛
- V V 2 V - تأثير القوى الداخلية (اللزوجة).
إن إثبات عدم وجود انفجارات (ووجود حلول) يعادل الدليل على أن السرعة القصوى لأي جزيء سائل تظل محدودة ببعض القيمة المحدودة. واحدة من أهم الكميات هي الطاقة الحركية للسائل.
عندما تبدأ في محاكاة التدفق باستخدام معادلات Navier-Stokes ، يكون للسائل قدرًا من الطاقة الأولية. في التدفقات المضطربة ، يمكن أن تبدأ الطاقة في التركيز. بدلاً من الانتشار المنتظم في جميع أنحاء النهر ، يمكن جمع الطاقة الحركية في دوامات صغيرة الحجم بشكل تعسفي ، ويمكن أن تتسارع الجسيمات في هذه الدوامات (نظريًا) إلى سرعة لا نهائية.
"مع الانتقال إلى مقاييس أصغر وأصغر ، تصبح الطاقة الحركية أقل وأقل فائدة للتحكم في القرار. يقول فلاد فيكول ، عالم الرياضيات في جامعة برينستون الذي كتب عملاً جديدًا مع تريستان بوكماستر: "يمكن للقرار أن يفعل أي شيء ، ولن أعرف كيف أتحكم به".
يصنف علماء الرياضيات المعادلات التفاضلية جزئيًا استنادًا إلى المدى الذي يمكن أن يبدأوا فيه بالتصرف بشكل سيئ على المقاييس الصغيرة بشكل لا نهائي. معادلات Navier-Stokes هي في نهاية هذا المقياس. يعكس تعقيد رياضيات المعادلات بمعنى ما مدى تعقيد التدفقات المضطربة التي يجب أن يكونوا قادرين على وصفها.
يقول فيكول: "عندما تقوم بتكبير مكان ما ، فعندئذٍ من وجهة نظر رياضية ، تفقد معلومات حول الحل". "لكن الاضطراب يجب أن يصف ذلك بالضبط - نقل الطاقة الحركية من المقاييس الكبيرة إلى الأصغر من أي وقت مضى ، لذلك يطلب منك حقًا التوسع."

بالحديث عن الخصائص الرياضية للمعادلات الفيزيائية ، من الطبيعي طرح سؤال: هل ستغير هذه الحجج الطريقة التي نعتبرها العالم المادي؟ في حالة معادلات Navier-Stokes ومشكلة الألفية ، سيكون الجواب "نعم" و "لا". بعد ما يقرب من 200 عام من التجارب ، من الواضح أن المعادلات تعمل: يتزامن التدفق الذي تنبأ به Navier-Stokes بالتتابع مع التدفق الملاحظ في التجارب. إذا كنت فيزيائيًا تعمل في أحد المختبرات ، فقد يكون هذا كافيًا لك. لكن علماء الرياضيات يحتاجون إلى معرفة المزيد - يريدون التحقق مما إذا كان من الممكن اتباع هذه المعادلات على طول الطريق لمراقبة كيف يتغير التدفق بالضبط من لحظة إلى أخرى (لأي تكوين مائع أولي) ، وحتى للقبض على مصدر الاضطراب.
يقول فيفرمان: "إن سلوك السوائل محفوف بالمفاجآت". "يتم تفسير هذه المفاجآت من حيث المبدأ من خلال المعادلات الأساسية التي تتحكم في تدفق السوائل ، ولكن كيفية الانتقال من المعادلات التي تتحكم في حركة المائع إلى وصف لكيفية تحرك المائع في الواقع أمر غامض."